花样滑冰怎样才能转得更快？
——质点系的运动定律和角动量定理

为什么杂技演员走钢丝时会手持长杆？花样滑冰时如何调节转动的角速度？杂技表演和花样滑冰都是我们平时收看电视节目或者网络节目时会遇到的，好奇的我们应该学会怎么用力学回答这两个问题。在前面我们学习过动量定理和相应的动量守恒定律，但是当时处理的是质点。如果我们面对的是多个质点或者是一个大小与形状无法忽略的物体，我们应该怎么分析其运动？为此，我们再次从牛顿定律出发，推导质点系的质心运动定律和角动量定理，并将角动量定理应用于刚体的定轴转动。然后，我们尝试利用这些结果对杂技表演中平衡杆的作用、花样滑冰时转速调节的原理进行解释。这些解释是定性的，我们无须做具体的计算。作为一个具体的可计算例子，我们将解决长杆在重力作用下的摆动问题，并分析它和单摆的区别。另一方面，我们以前在没有使用角动量概念的情况下推导了开普勒第二定律。在这里，我们将证明，开普勒第二定律是角动量定理的简单推论。

一、质点系的质心运动定律：牛顿定律的简单叠加

为了突出重点，我们先从简单的两质点系统入手。假设两个质点的质量分别是 m ₁ 和 m ₂ ，它们各自受到的合力分别为：

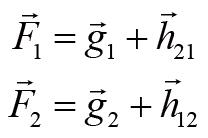
其中用字母 g 表示的是外力，用字母 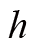表示的是两质点之间的相互作用力，下标21表示质点2对质点1的作用，下标12表示质点1对质点2的作用。这里只考虑力 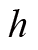的方向平行于两质点连线的情况。利用牛顿第二运动定律 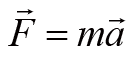，两个质点会产生两个方程，二者相加会得到组合的运动方程：

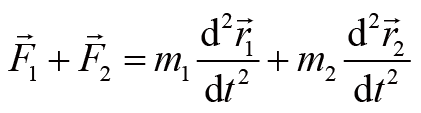（1）

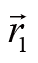其中 和 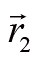分别表示两个质点的位置。将前面合力的表达式代入等式左边，有：

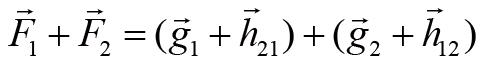
考虑到牛顿第三定律， ，所以：

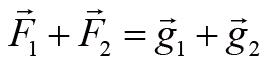
我们再回到式（1），它的等号右边可以改写为

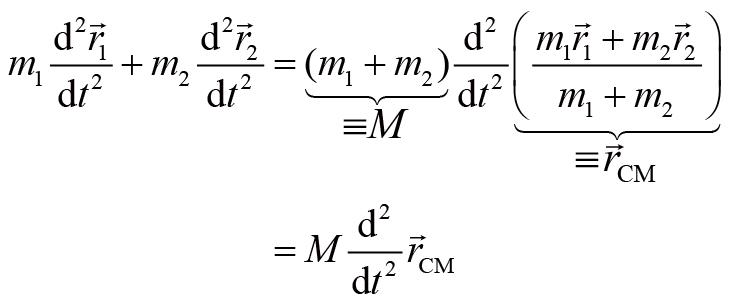
上式中的 M 是总质量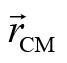， 是质心坐标。将前面的结果综合起来，我们会得到：

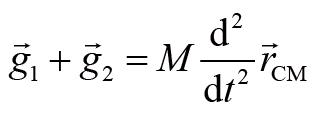
这个方程描述的是质心怎么随着时间改变，因此被称为质心运动定律。又因为系统的总动量为：

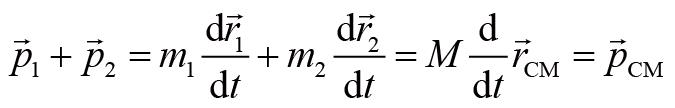
所以质心运动定律可以改写为：

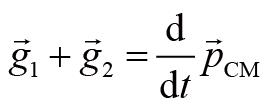
质心运动定律描述的是系统总动量随时间的变化情况：系统总动量在单位时间的改变量等于总外力。因此，质心运动定律又被称为质点系的动量定理。

这里的结果可以推广到多质点的情况，质点之间的相互作用力会互相抵消，最终只剩下外力。所以对于多质点的情况，等式左边依然是质点系受到的合外力，右边是总质量乘以质心加速度，形式与牛顿定律类似。

二、质点系的角动量定理：总角动量变化率等于合外力矩

质心运动定律虽然形式简单，但是已经丢失了系统的很多信息。就像 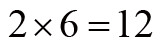与 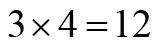一样，如果只知道最后结果是12，是不能确定原来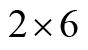是 还是 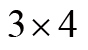的。所以，只要我们回到各个质点的原始运动方程，我们会获得更多关于系统的信息。但是对于质点系，我们一般只知道它所受的外力，质点之间的相互作用力在很多情况下都非常复杂，质心运动定律的推导过程中刚好把质点之间的“内力”都消掉了。那还有没有别的方法能得到关于系统的新的信息而又不会涉及质点间的作用力的呢？还是有的，接下来我们要介绍的角动量定理就满足此要求。

我们先考虑单质点的情况。质点的运动方程为：

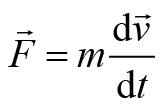
我们定义力 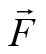对质点的力矩为质点的位置矢量 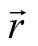与这个力的叉乘。用 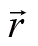同时与上式的两端做叉乘，我们有：

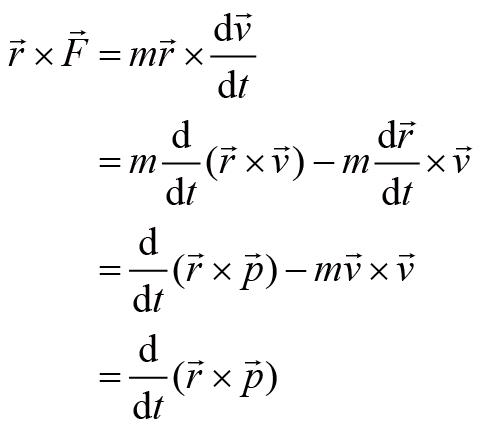
我们将 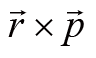定义为质点的角动量 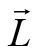，也就是：

这就是单质点的角动量定理：角动量在单位时间内的改变量等于质点所受力矩。

在单质点角动量定理的基础上，考虑两个质点的情况。与证明质心运动定律类似，对两质点分别应用角动量定理，这样我们会得到两个方程，然后我们将这两个方程叠加在一起，会得到：

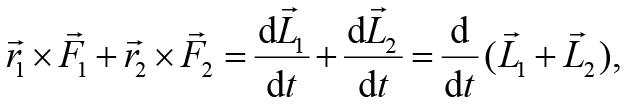
其中的数字下标分别对应两个质点。使用我们前面推导质心运动定律时所用的符号，上式中的力矩之和可以改写为

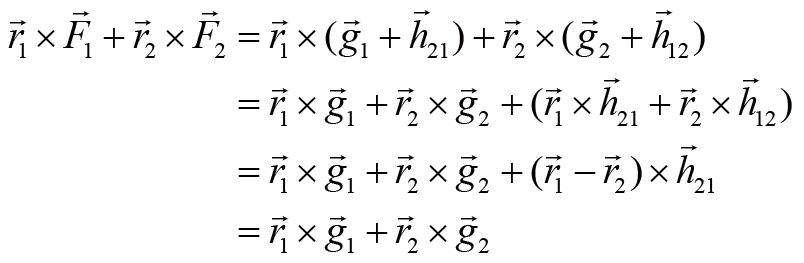
最后一个等式之所以成立，是因为我们只考虑质点之间相互作用力平行于质点间连线的情况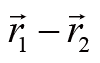， 等于质点2到质点1的位移矢量，所以它与 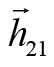平行，从而叉乘的结果为0。上式最终的结果正好是两个质点的合外力矩。于是，总角动量在单位时间内的改变量等于外力矩之和。这个结论可以推广到多质点的情况。如果用 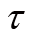表示外力矩，那么角动量定理可以写为：

或者通过各个外力与各个质点的角动量表示为：

三、角动量定理在刚体定轴转动上的应用

前面的角动量定理是在离散的情况下推导出来的，不过也能应用到连续的刚体上。有一点需要注意的是，在体积不可忽略的物体上的质量微元，它们之间的切应力并不平行于质量微元之间的连线。这似乎表明角动量定理不能用在刚体上。所幸的是，切应力只作用在接触面上，因此作用力和反作用力的作用位置相同，从而求其力矩时所用的位置矢量也相同，力矩叠加在一起后切应力部分正好互相抵消。总的来说，角动量定理依然可以应用到连续的物体上，包括刚体。

刚体的运动是复杂的，即使考虑刚体绕着一个固定点转动，其转动轴也可能时刻改变。简单起见，我们这里只考虑刚体绕着固定轴转动的情况。以刚体的转动轴为 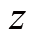轴建立柱坐标系，与 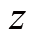轴垂直的坐标面使用的是极坐标。考虑刚体上的一小块质量，把它看成第 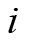个质点，它的角动量为：

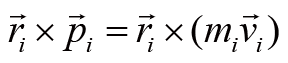（2）

在定轴转动的情况下，刚体上的质点做的是圆周运动，利用圆周运动的相关结论，我们有：

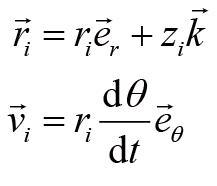
其中角度 θ 没有标注下标 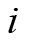，是因为在定轴转动的情况中刚体每一点（轴心上的点除外）的角速度都是一样的。在定轴转动的情况下，我们只需要考虑 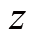分量的角动量定理，其他分量会牵扯到转轴施加给刚体的力矩，这不在我们考虑的范围内。将上式代入式（2），并利用基矢叉乘关系：

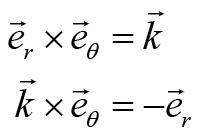
可以得到该质点角动量的 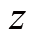分量为：

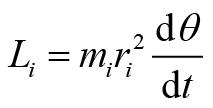
质点 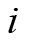的角动量还包含径向分量，不过基矢 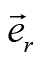对时间的导数正比于基矢 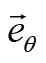，不会对 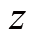方向产生任何影响，因此可以在考虑角动量对时间导数的 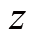分量时把质点 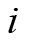角动量的径向分量忽略掉。

注意到刚体定轴转动下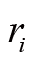， 不会随时间变化，于是刚体总角动量对时间的导数的 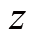分量为：

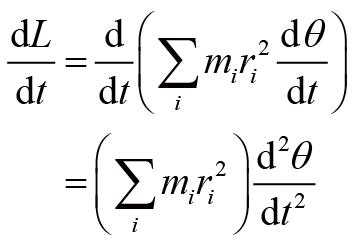
后文为了表述的简洁性，将把角动量的 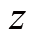分量简称为角动量。定义刚体的转动惯量为：

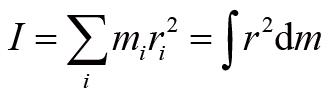
那么刚体角动量随时间的变化率可以写为：

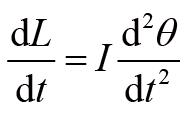
接着，我们考虑质点 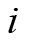受到的 z 方向的外力矩：

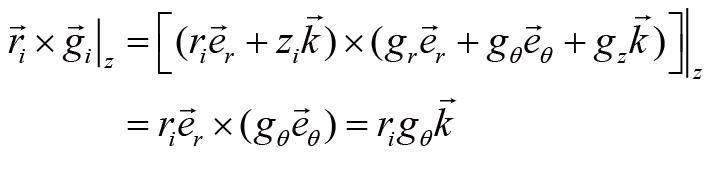
将合外力矩叠加在一起，结合角动量定理，我们有：

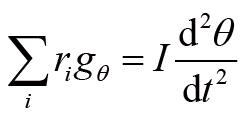
这就是刚体定轴转动的角动量定理。它在形式上和牛顿第二定律非常相似，等式右边是转动惯量与角加速度的乘积，正如质量衡量的是物体运动状态改变的难易程度，转动惯量衡量的是刚体转动状态改变的难易程度。在牛顿第二定律中，力是改变物体运动的原因，而在角动量定理中，力矩是改变刚体转动的原因。

如果外力矩等于0，那么 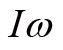为常数，不随时间变化。 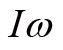正好是刚体定轴转动时的角动量，所以刚体的角动量在外力矩为0时保持不变，这就是刚体的角动量守恒定律。

角动量定理和角动量守恒定律可以帮助我们理解生活中的一些问题。我们先以花样滑冰运动员在冰上的转动为例。运动员转动时会做各种动作，虽然不能看成刚体，但角动量守恒依然成立。运动员在冰面受到的摩擦力可忽略不计，重力与支持力相互抵消，可以近似看成不受外力作用。当运动员转动过程中，如果将手缩回，则转动惯量公式中与手对应的 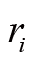变小了，从而运动员的转动惯量也将变小。因为角动量保持不变，所以运动员的角速度 ω 必然会增大。反之，如果运动员的手伸张出去，角速度则会变小。

另一个例子是，杂技演员在走钢丝时一般都会手持一根长杆，这是为什么呢？这是因为，杂技演员手中的长杆可以助其提高转动惯量，从而在受到同等大小的力矩扰动的情况下，手持长杆会比没有持长杆的角速度改变量要小，杂技演员也因此更容易恢复平衡。

四、物理摆

作为刚体角动量定理的应用，我们计算一下物理摆的运动方程。所谓物理摆，指的是线密度均匀的长杆在重力作用下绕着其一个端点自由摆动的系统。这是一个刚体定轴转动的模型。假设长杆的质量线密度为 ц ，长度为 L ，那么它的转动惯量为：

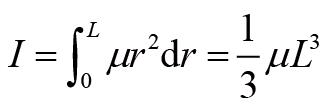
对长杆的力矩贡献不为0的只有重力，重力矩为：

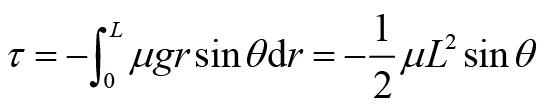
利用前面推导出来的角动量定理，我们有：

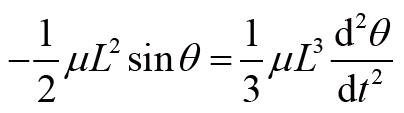
化简上式，我们得到：

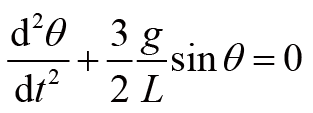（3）

这个结果是不平凡的。为什么这么说呢？如果我们简单地把长杆看成所有质量集中于长杆质心处的物体，利用牛顿定律，我们会得到如下的“运动方程”：

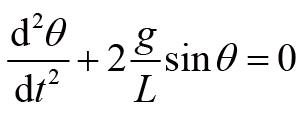
此式与我们严格推导出来的式（3）差别比较大，因此，不能简单地把物体的所有质量等效到质心处。回到式（3）上来，虽然它本身比较复杂，不能简单地求解，但是当摆动角很小时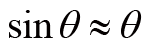， ，在此近似下我们有：

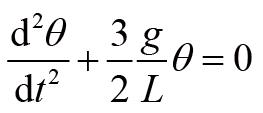
这个方程与谐振子的振动方程类似，我们可以借助谐振子的相关结论得到小幅度物理摆的角频率为：

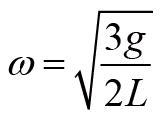
频率和周期分别为：

五、证明开普勒第二定律

还记得我们前面在求解物体在万有引力下的运动轨迹时顺便证明的开普勒第二定律吧？当时我们在极坐标下展开牛顿第二定律，发现角向方程本质上是一个常量的导数，最终得到了开普勒第二定律。在这里，我们将证明开普勒第二定律本质上是角动量守恒定律。

我们在前文推导了单质点的角动量定理，这个定理在中心力场中能起到简化问题的作用，这是因为当我们把坐标原点取为力的中心时，力矩自然为0。引力场作为典型的中心力场，对其中的物体应用角动量定理是自然而然的选择。

在质量为 M 的星球的引力场中，质量为 m 的质点受到的引力为：

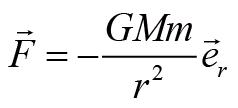
所以质点受到的力矩为：

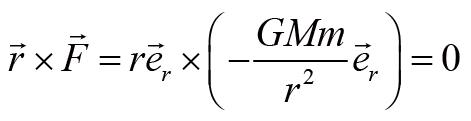
可见引力矩为0。根据角动量定理，质点的角动量不随时间变化。接下来，我们在柱坐标下推导质点的角动量。我们先写出质点角动量的一般公式：

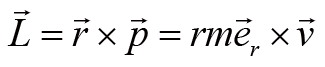（4）

其中 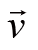是粒子的速度。以质点的轨迹平面为极坐标面，星球所在位置为原点，建立柱坐标系，那么粒子的速度矢量可以写为：

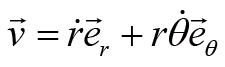
其中字母上方加一点表示这个量对时间的一阶导数。将上式代入式（4）后可得：

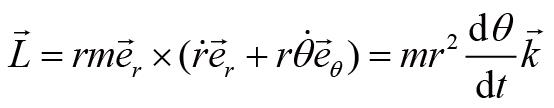
由于角动量守恒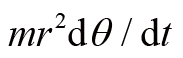， 不随时间变化。

为了理解这个结果，我们考虑质点和星球的连线，d θ 是这根线在 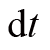时间内转过的角度，因此 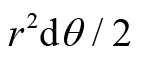是这根线在 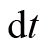时间内扫过的面积。换言之，这根连线在单位时间内扫过的面积为常数，这就是开普勒第二定律。可见，开普勒第二定律是角动量守恒定律的简单推论。

小结

在这一节，我们从基础的牛顿定律出发，推导了质点系的动量定理和角动量定理。质点系的动量定理又被称为质心运动定律，它表明我们可以在忽视内力的情况下把整个系统集中到质心，然后对这个等效质点应用牛顿第二定律。质心运动定律描述了系统整体的运动，而角动量定理则描述了系统怎么“旋转”。我们将角动量定理应用到定轴转动的刚体上之后，得到了一个形式上和牛顿第二定律非常相似的方程，这有助于加深我们对角动量定理的理解。紧接着，我们使用推导出来的结论计算了物理摆的运动方程，得到了它在小角度摆动情况下的频率与周期，同时表明了在摆动问题上，不能简单地把物体所有质量集中于质心来处理。最后，我们证明了开普勒第二定律是角动量守恒定律的一个简单推论，这给了我们从另一个视角理解开普勒第二定律的机会。结合以前我们在没有使用角动量的情况下推导开普勒第二定律的过程，我们可以感受到物理体系的内在和谐。 CUDOQnpYk1lBLO53/iqfa1ub8hqHN2d5nYrpbBtMiYLZbQYF8r3zKcY2jM6fLQhr