




稳定性(stability)是系统设计追求的目标。具有稳定性的系统称为稳定系统(stable system)。所谓稳定系统,就是当系统输入有界时,系统的输出也有界,即有界的输入产生有界的输出。在数学上可以表示为
若 | x ( n )|≤ M x <∞, 则| y ( n )|≤ M y <∞
线性时不变系统具有稳定性的充要条件:系统的单位冲激响应绝对可和,即

例1—28
判断累加器系统
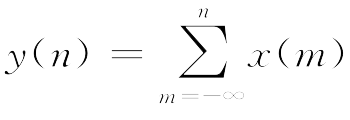 的因果性和稳定性。
的因果性和稳定性。
解: (1)根据定义判断
因果性:
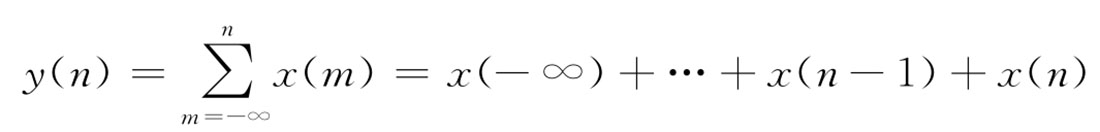
可见累加器系统的输出只与以前和当前的输入有关,与未来的输入无关,所以累加器系统具有因果性,是因果系统。
稳定性:首先假设输入 x ( n )有界,| x ( n )|≤ M x <∞,虽然每一个输入序列的值有界,但是累加器运算需要从-∞时刻累加到 n 时刻,当累加项数无穷大时,累加器的输出 y ( n )→∞,所以累加器系统是不稳定的。
(2)根据线性时不变系统因果性和稳定性的充要条件判断
由于累加器系统是一个线性时不变系统,因此可以利用线性时不变系统因果性和稳定性的充要条件加以判断。
因果性:累加器系统的单位冲激响应为
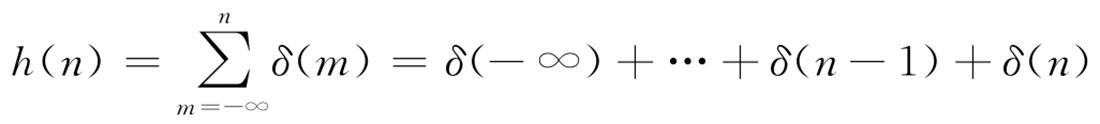
当 n <0时,因为 δ ( n )=0,所以
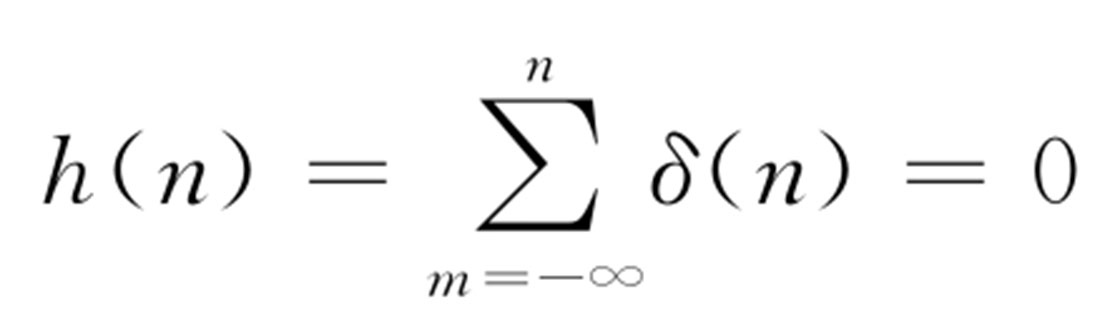
因此系统满足因果性。
稳定性:
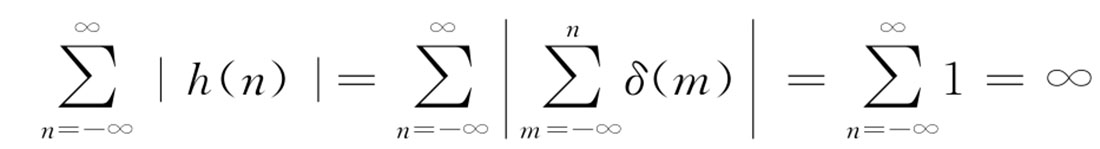
可见累加器系统的单位冲激响应不是绝对可和的,因此该系统不满足稳定性。
利用上述两种判别方式都证明了累加器系统是一个因果但不稳定的系统。