




神经网络算法是常用的分类和回归算法,有很多不同形式,深度学习在广义上也属于神经网络(见3.14节),本节集中在经典的模型。首先以人工神经网络(Artificial Neural Network,ANN)模型为例,形象展示神经网络模型的逼近能力。然后以一个特定模型极限学习机(Extreme Learning Machine,ELM)为例,让大家理解网络模型可以变化或扩展的方面有很多。
ANN是一个三层结构的网络,包括输入层、隐含层和输出层,可以用来做回归或分类。在增加隐含层节点的前提下,ANN的算法具有无限的函数逼近能力,在工业中有广泛的应用 [23] 。ANN的逼近能力在理论层面可由数学证明,本节仅从分段逼近的角度,直观演示ANN的逼近能力。最后,也说明,实际的神经网络模型训练基于梯度下降算法,学习结果并不是按照分段逼近。
1.当权重参数大时,sigmoid函数可近似为一个阶跃函数
为简明起见,这里仅仅讨论单变量的情形(多变量的情形类似)。
神经元通常采用sigmoid函数,是将输入 x ∈(-∞,+∞)映射到(0,1),包含了权重系数 w 和偏移系数 b 这两个参数:
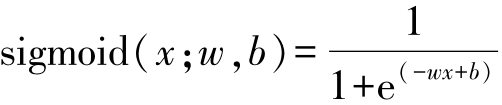
当 w 比较大的时候,sigmoid函数接近一个阶跃函数,如图3-22所示。
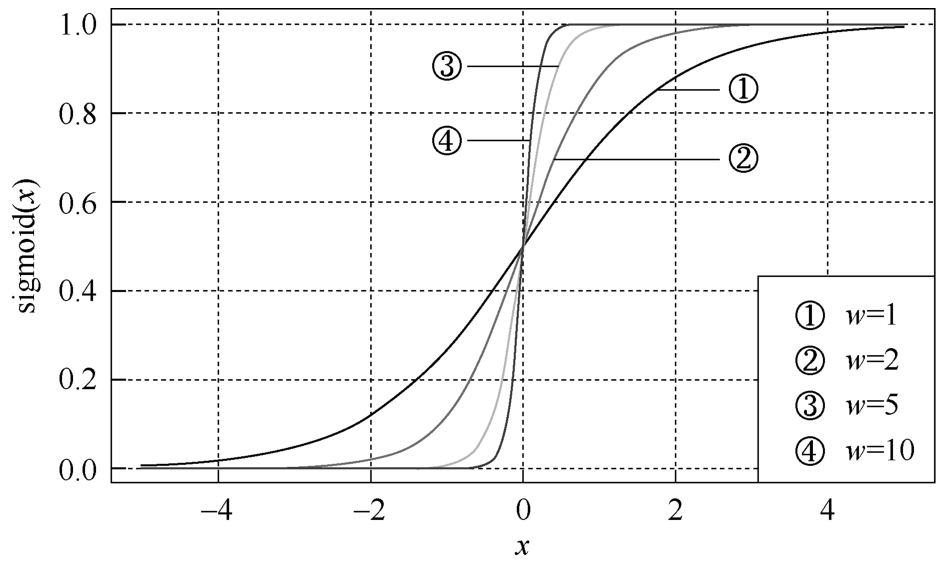
图3-22 不同权重系数下,sigmoid函数的形状
2.多个阶跃函数通过不同的偏移参数和加权,可以构成复杂的分段函数
当 w 比较大时,sigmoid函数比较接近阶跃函数, b/w 决定了阶跃发生的位置,如图3-23所示。
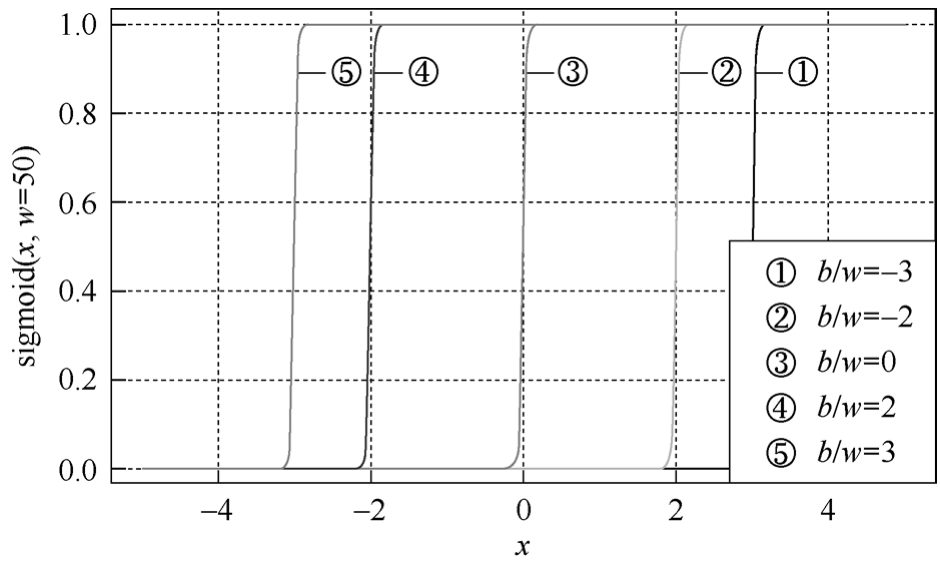
图3-23 不同 b/w 下,sigmoid函数的形状
这里标记 s = b/w ,假设 w 固定为一个很大的数值,sigmoid函数可以简记为 g ( x ; s )。两个sigmoid函数通过不同 s 参数和加权系数 h ,即 h 1 · g ( x ; s 1 )+ h 2 · g ( x ; s 2 )可以构成3分段函数。如图3-24a~b所示。特别是图3-24b,如果 h 1 = -h 2 ,则可以通过2个神经元对构成一个局部化的方形区域,基于这样的组合,我们可以很容易去构建更加复杂的组合。如果有多个组合,可以组成为更复杂的分段函数,如图3-24c所示。
因此,对于一个如图3-24d所示实际的函数,可以先分段矩形逼近,然后按照图3-24b的神经元对的方式,去构建对应的神经网络模型。这样就可以理解成,如果增加隐含节点,ANN有无限的逼近能力。
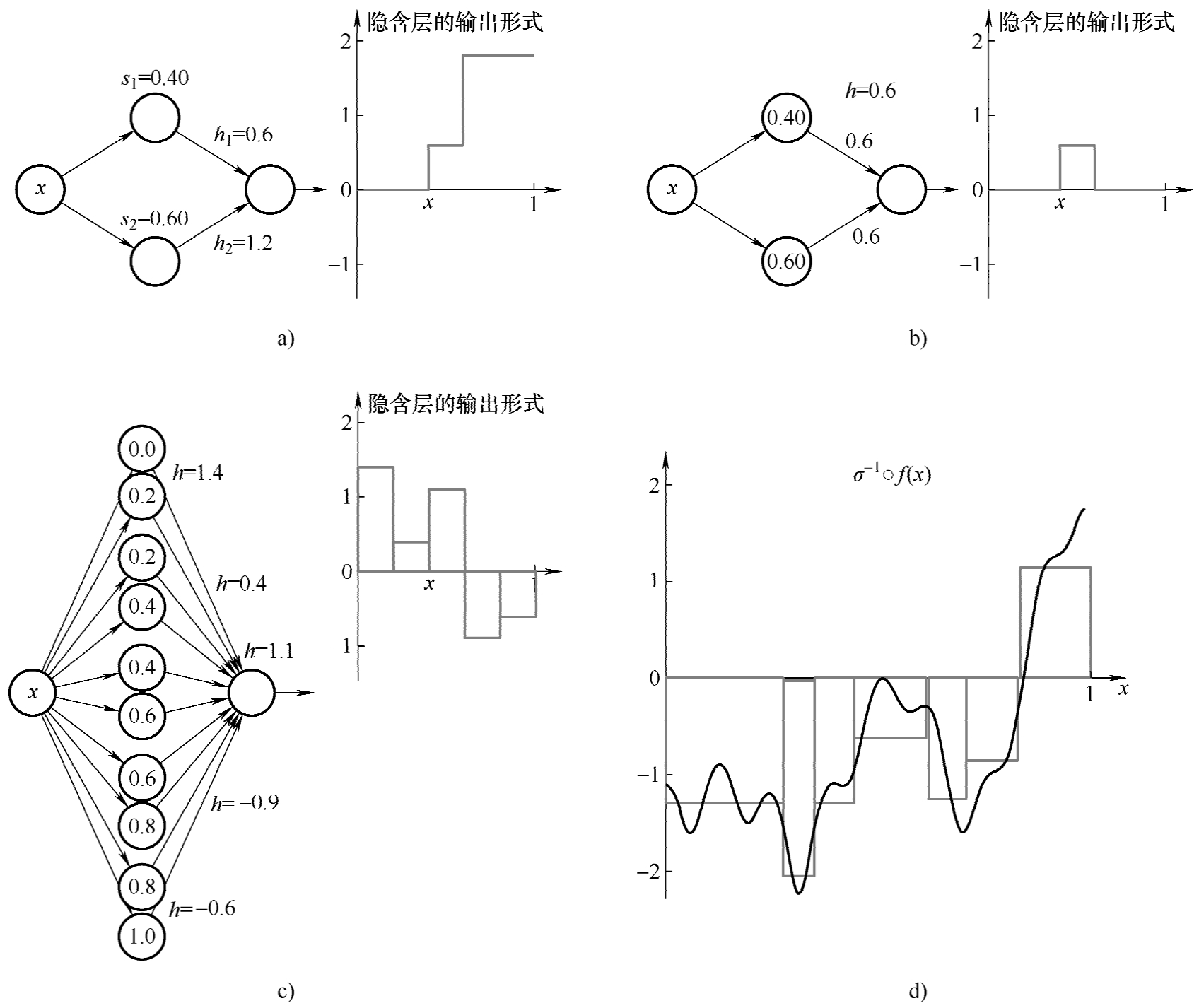
图3-24 不同组合下的神经网络形态
3.实际ANN模型不是简单的分段逼近,而是损失函数的梯度下降与反向传播
以下面解析表达式在[0,1]区间内的曲线为例,看看ANN模型的逼近过程,图3-24d曲线就是这个表达式(只是均值移除):
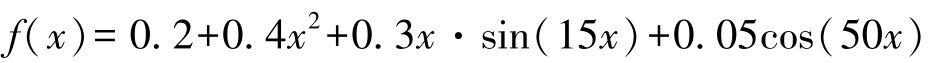
按照上面的分段线性法,设置 w =100,我们将[0,1]平分为5段,进行参数的估算,作为10个隐含节点的参数,这样神经网络模型有31个参数(输入—隐含层的10个权重参数,隐含节点的偏移量10个参数,隐含—输出层的10个权重参数,输出层的偏移量1个参数)。并按照R里面nnet包中模型参数规范组织,作为nnet()函数的初始参数:

31个估算参数与训练后的神经网络模型参数如下所示,二者明显不同:


拟合结果如图3-25所示,其中Groundtruth为原始曲线,Initial是初估参数的拟合曲线,Final是nnet()训练出来的曲线。
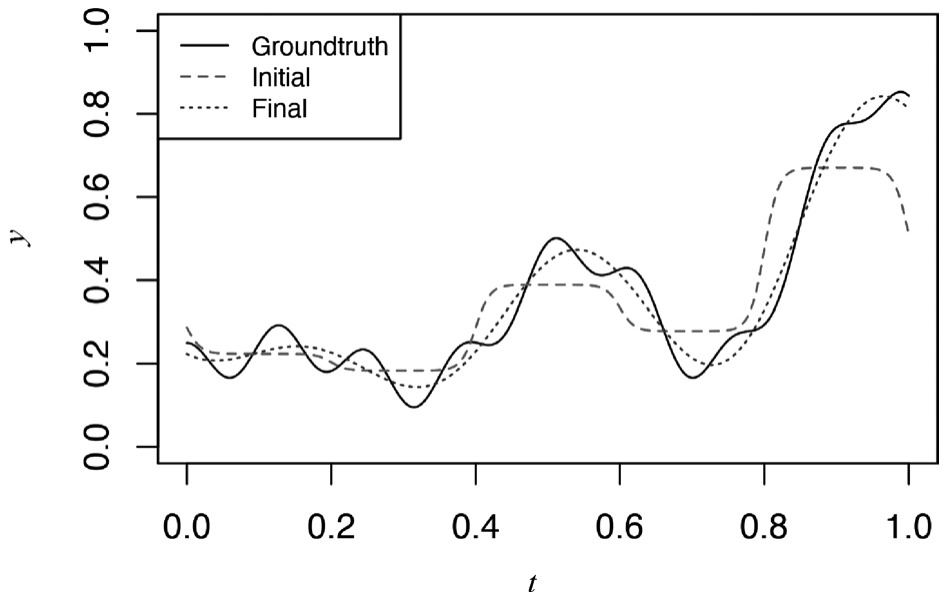
图3-25 初始效果和拟合结果
为更清楚理解ANN通过隐含层逼近的过程,我们选择3个隐含层的神经网络模型,如下述代码和图3-26所示,可以看到3个隐含层的Sigmoid函数比较简单,3个核函数的偏移量不同,可以想像,Kernel 1与2组合,可以把[0,0.2]区间控制在一个比较低的水平,同时[0.3,0.5]的上升区间能够很好地实现逼近,然后再通过Kernel 3做反向修正。通过本例,期望大家可以理解ANN“神奇”背后的朴素思想,其实就是通过参数优化选择比较好的Kernel函数形式,然后通过合适的权重系数去逼近目标曲线(从数学意义上,可以叫泛函)。


为了更好地理解背后的工作机制,读者也可以自行尝试不同的简单函数关系下神经网络各层的参数和函数形式,例如: y = x 、 y = x 2 、 y =1 /x 、 y =sin( x )。
ANN模型训练背后基于梯度下降算法,因此,要求输入变量间不能存在多重共线性,否则容易出现不收敛的情形。另外,梯度下降速度过快,容易引起“早熟”,即模型过早陷到一个局部最优解,无法获取全局最优解。更深入的控制方法可以参阅参考文献[24]。
极限学习机(Extreme Learning Machine,ELM)模型的网络结构与ANN一样,只不过在训练阶段不再是基于梯度的后向传播算法,而是随机初始化输入层的权值和偏差,输出层权重则通过广义逆矩阵理论计算得到。这样,ELM算法比传统神经网络的准确度略差,但计算量降低很多,可以被用于需要即时计算的场景中。
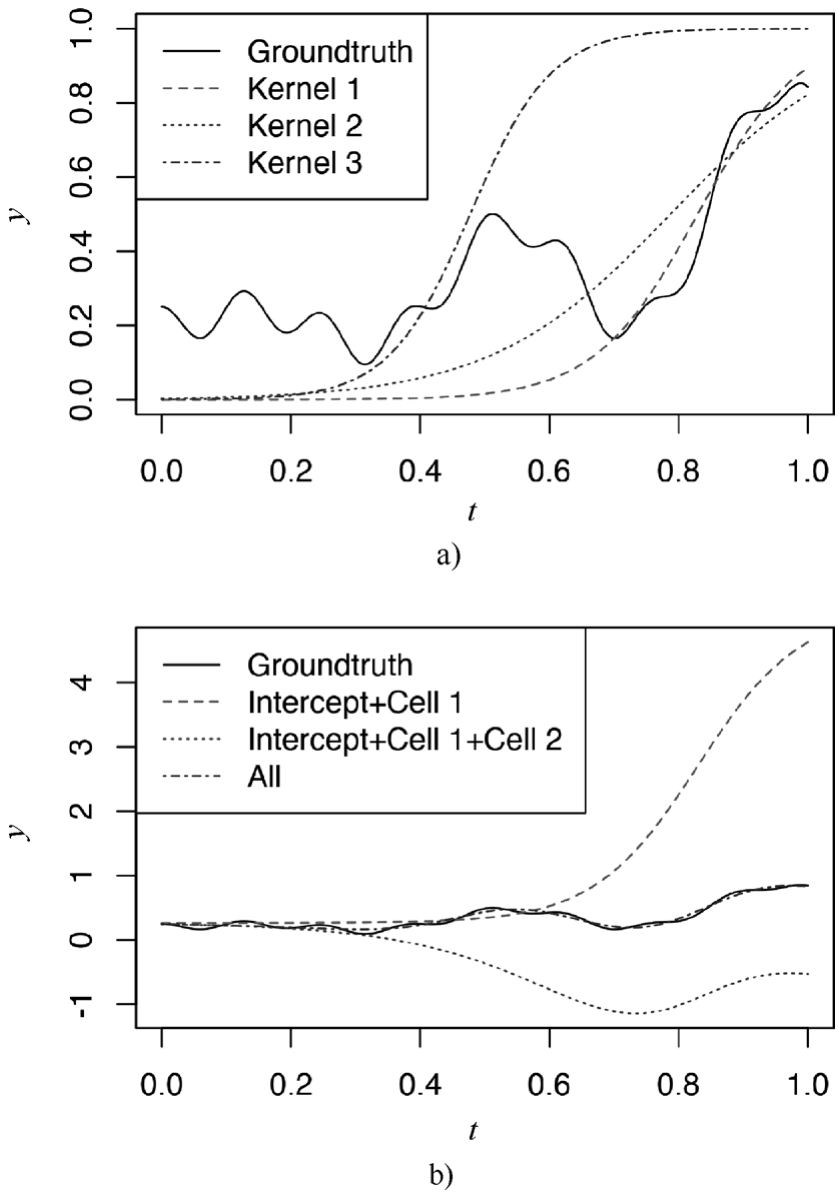
图3-26 3个隐含层的神经网络模型
极限学习机不是一个新概念,只是在算法(方法)上有新的内容。在神经网络结构上,就是一个前向传播的神经网络。主要有以下两点不同。
1)输入层和隐含层的连接权值{ w i }、隐含层的阈值{ b i }可以随机设定,且设定完后不用再调整。这和传统神经网络不一样,传统神经网络需要不断反向去调整权值和阈值。因此这里就能减少一半的运算量了。
2)隐含层和输出层之间的连接权值{ β k }不需要迭代调整,而是通过解方程组方式一次性确定。根据 w , b 和隐含层的激活函数,可以计算隐含层输出 H ,假设目标函数输出为 T ,对于回归问题,就是求解min‖ Hβ-T ‖ 2 ,这样就转化为求解矩阵 H 的广义逆(Moore-Penrose)矩阵问题,该问题有正交投影法、正交化法、迭代法和奇异值分解法(SVD)等集中求解方法。
R中elmNN包(以及基于它的Rcpp的新实现的elmNNRcpp包)和ELMR包 [25] 。下面用源代码方式来展示ELM的训练过程。
构建一个单变量的复杂函数,均值函数为
f
(
x
)=sin(8
x
-4)+
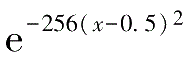 ,如下述代码和图3-27所示。
,如下述代码和图3-27所示。

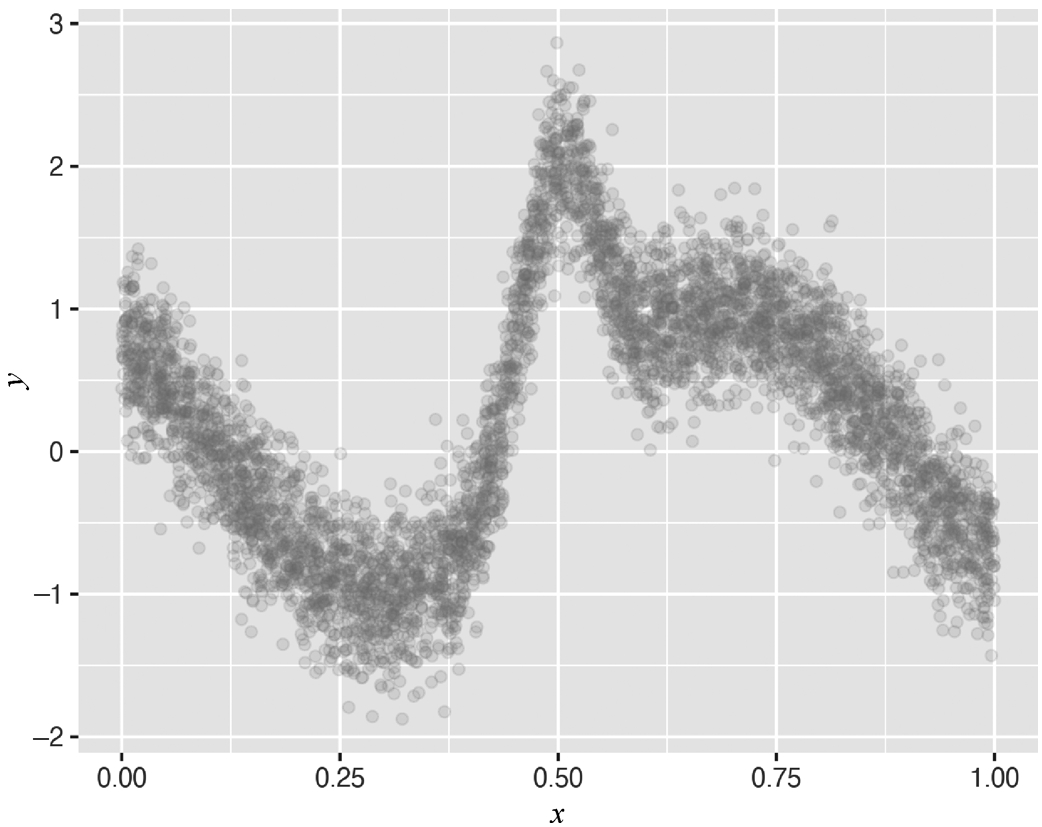
图3-27 拟合结果
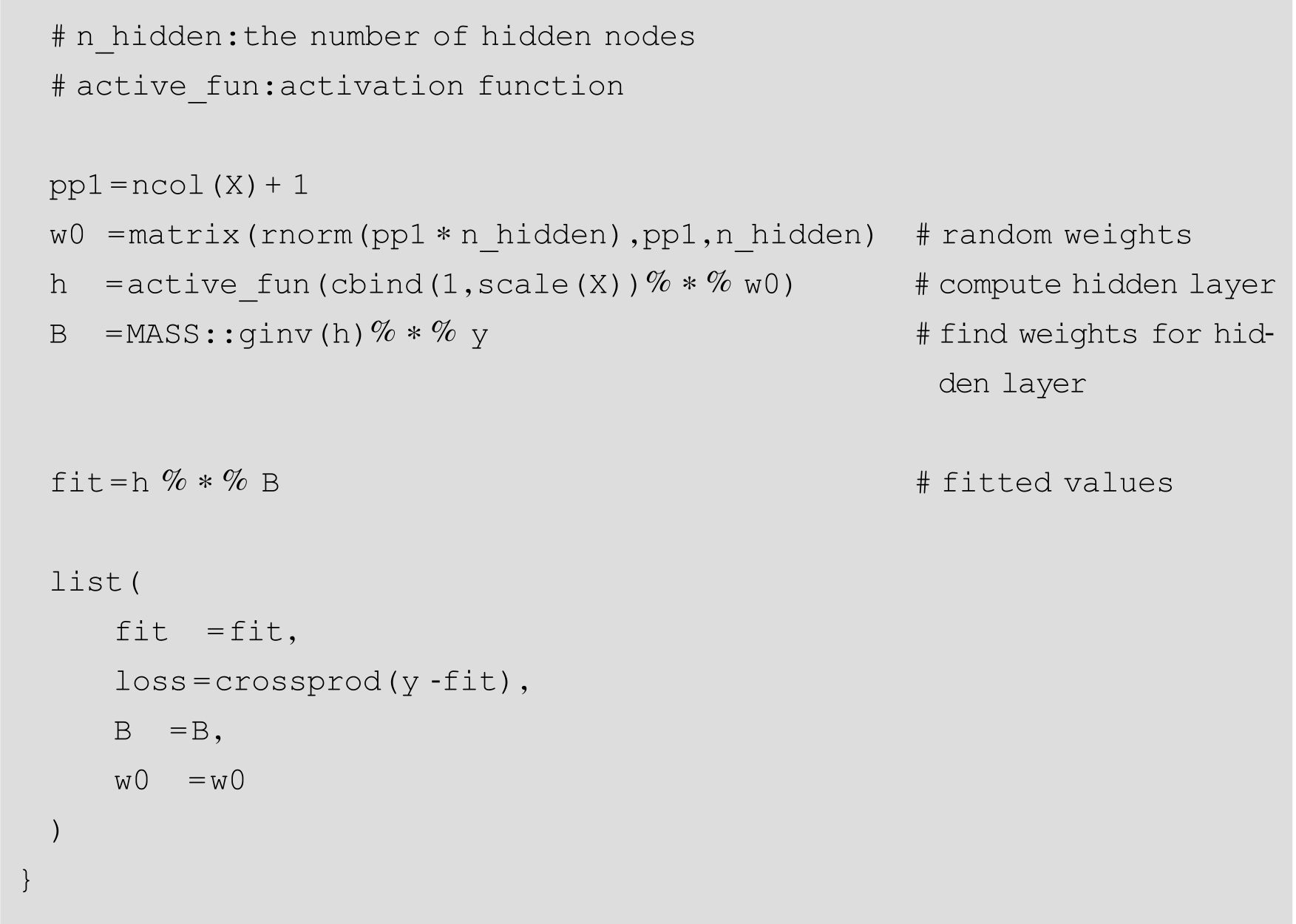
构建ELM函数,包括模型的拟合函数,函数的返回值是一个List对象:

采用前面的数据集进行ELM模型拟合,如下述代码和图3-28所示。

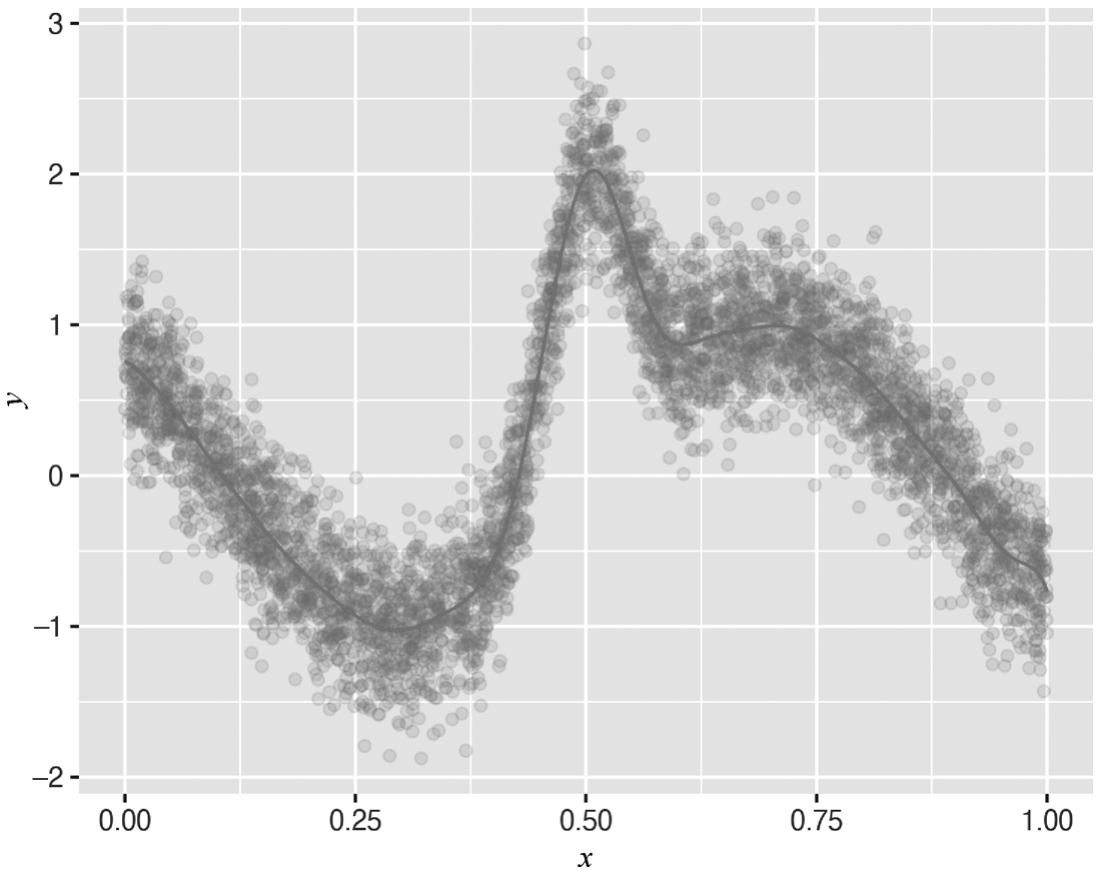
图3-28 拟合结果
GAM(Generalized Additive Model,广义加性模型)作为半参数方法,拟合能力比较强。将ELM的拟合结果与GAM(采用高斯过程)对比,可以看出ELM的拟合结果与GAM相差不多,如下述代码和图3-29所示。
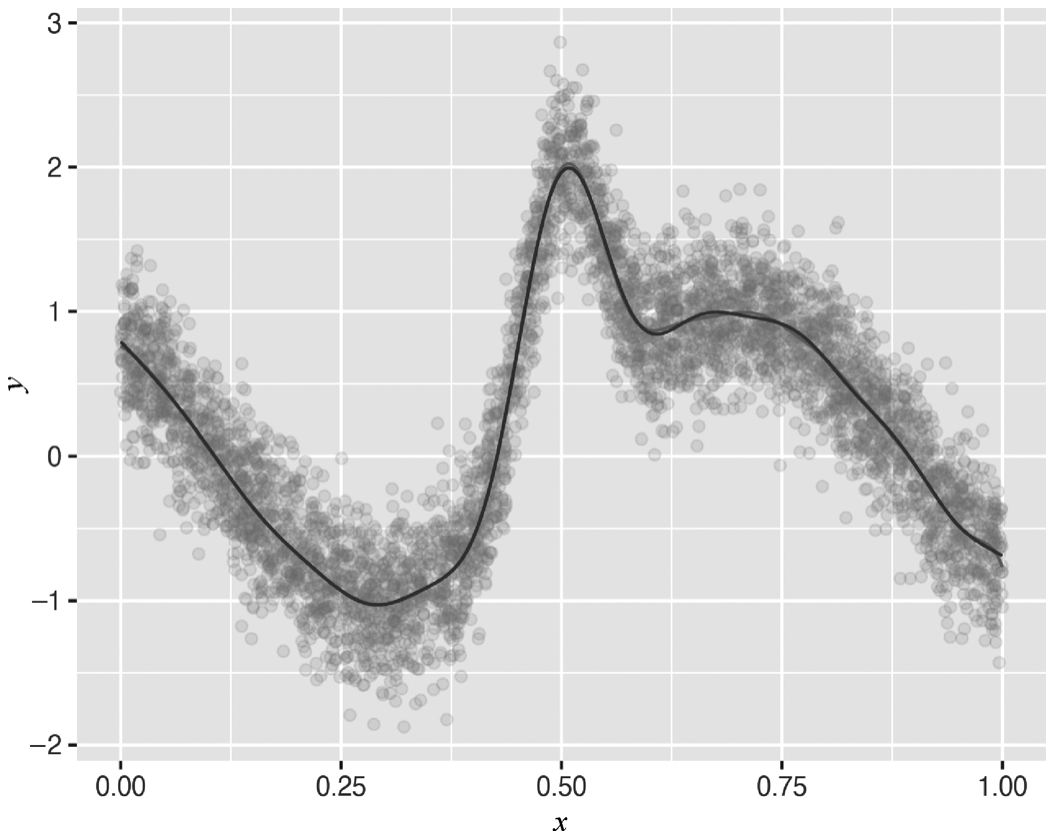
图3-29 拟合结果
