




统计分析是一套有关数据收集、处理、分析、解释并得出结论的方法体系,分为描述性统计和推断两部分。
描述性统计是在实际数据分析中最基础、应用最广泛的方法,它使用表格、图形和数值方法汇总和描述数据 [1] 。数据的概括性度量如图3-1所示,数据图形展示如图3-2所示。
推断统计是利用样本数据推断总体特征的统计方法,具体来说,推断统计以概率论为基础,根据抽样样本,对总体的分布进行参数估计和假设检验,如图3-3所示。因此推断统计主要涉及与概率分布、参数估计和假设检验相关的算法。
令待推断总体的概率分布为 p θ , θ 是概率分布的参数集合,目标是推断 θ 的某种性质。 p θ 也被称为统计模型,根据 θ 参数空间的数学性质,可以将统计模型分为两类:参数统计模型 [2] 和非参数统计模型 [3] 。在参数统计模型中,参数集属于有限维空间,参数空间的维度 d 被称为参数统计模型的自由度;而在非参数统计模型中,参数集属于无穷维空间,即 p θ 无法被有限数量的分布参数指定。
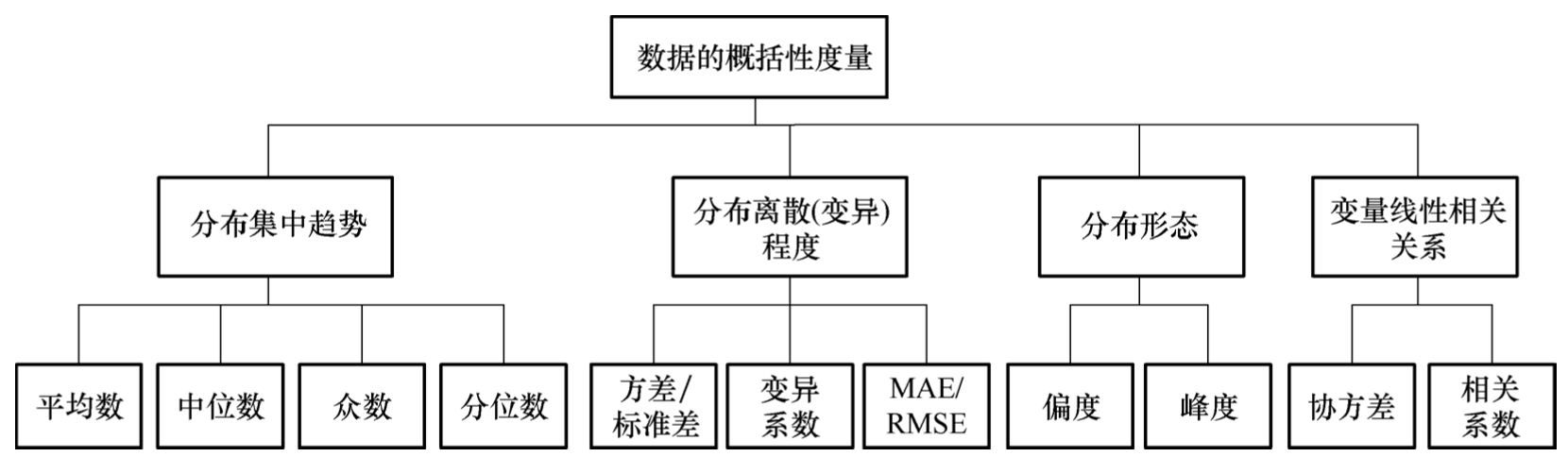
图3-1 数据的概括性度量
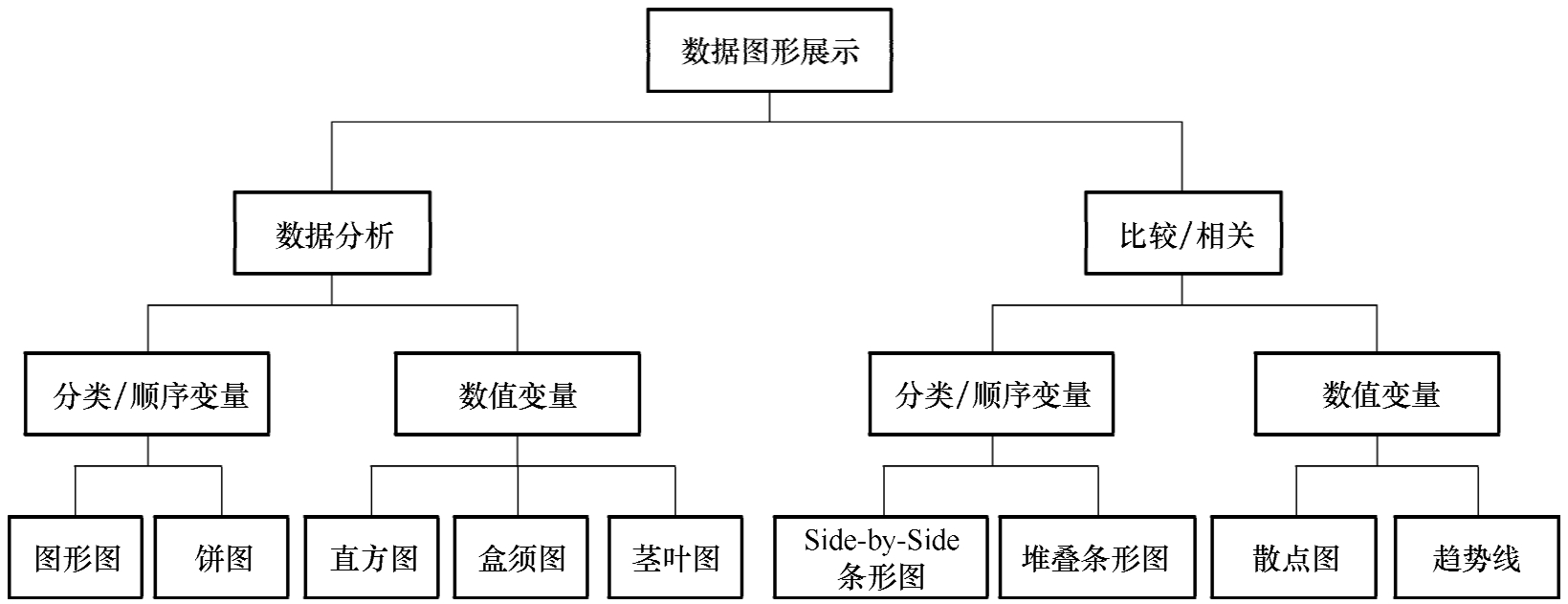
图3-2 数据图形展示
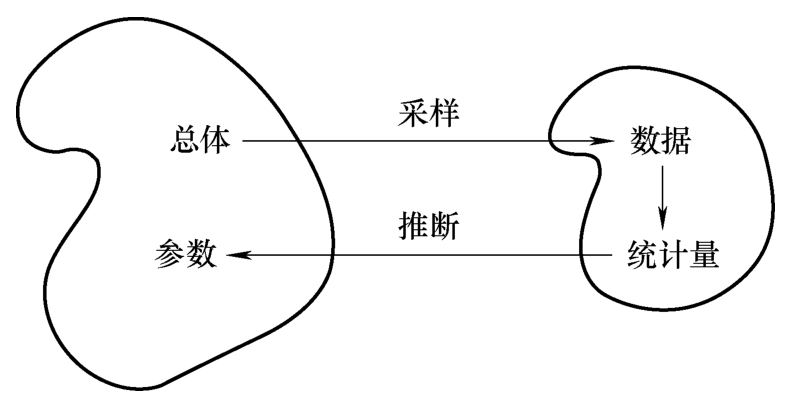
图3-3 推断统计的概念
当实际数据分布比较复杂或者没有先验知识时,很难选择一个合适的参数化的概率模型,这时非参数化估计方法更加灵活。核函数(局部相似)、随机仿真[蒙特卡罗方法(Monte Carlo method)]是常用的非参数化统计思路。核函数是概率密度估计的常用方法。随机仿真包括随机样本生成(按照一定的概率分布函数)和随机采样等方式,思路容易理解,并且不仅仅可以在既有数据集上进行,也可以结合模型进行随机仿真,例如,在SSA(奇异值分解)预测量的置信区间估计时,就是对当前SSA模型的重构误差进行建模,用误差模型生成若干随机序列,与原始的重构序列(趋势项)相加得到新的序列,让SSA算法对每个新序列重构并预测,从多个预测值获得置信区间估计。
与非参数模型相比,有参数模型描述采样数据分布时容易存在更多偏差,但是有参数概率分布的优势是,可以用很小的参数空间拟合数据分布,提升建模效率。因此,对数据进行统计推断的第1步是通过观察统计实验样本的直方图,从概率分布家族中选择一个有参数分布作为假设分布。概率分布拟合的数值计算方法将在下节详细讨论。
常见的概率分布及其关系如图3-4所示。其中常见的离散概率分布包括二项分布、泊松分布、几何分布;连续分布包括均匀分布、正态分布、 t 分布、 χ 2 分布、 F 分布、指数分布等。在拿到一组数据,并绘制出分布直方图后,如何判断数据符合什么分布呢?概率分布判断流程如图3-5所示,建议从4个方面进行判断。
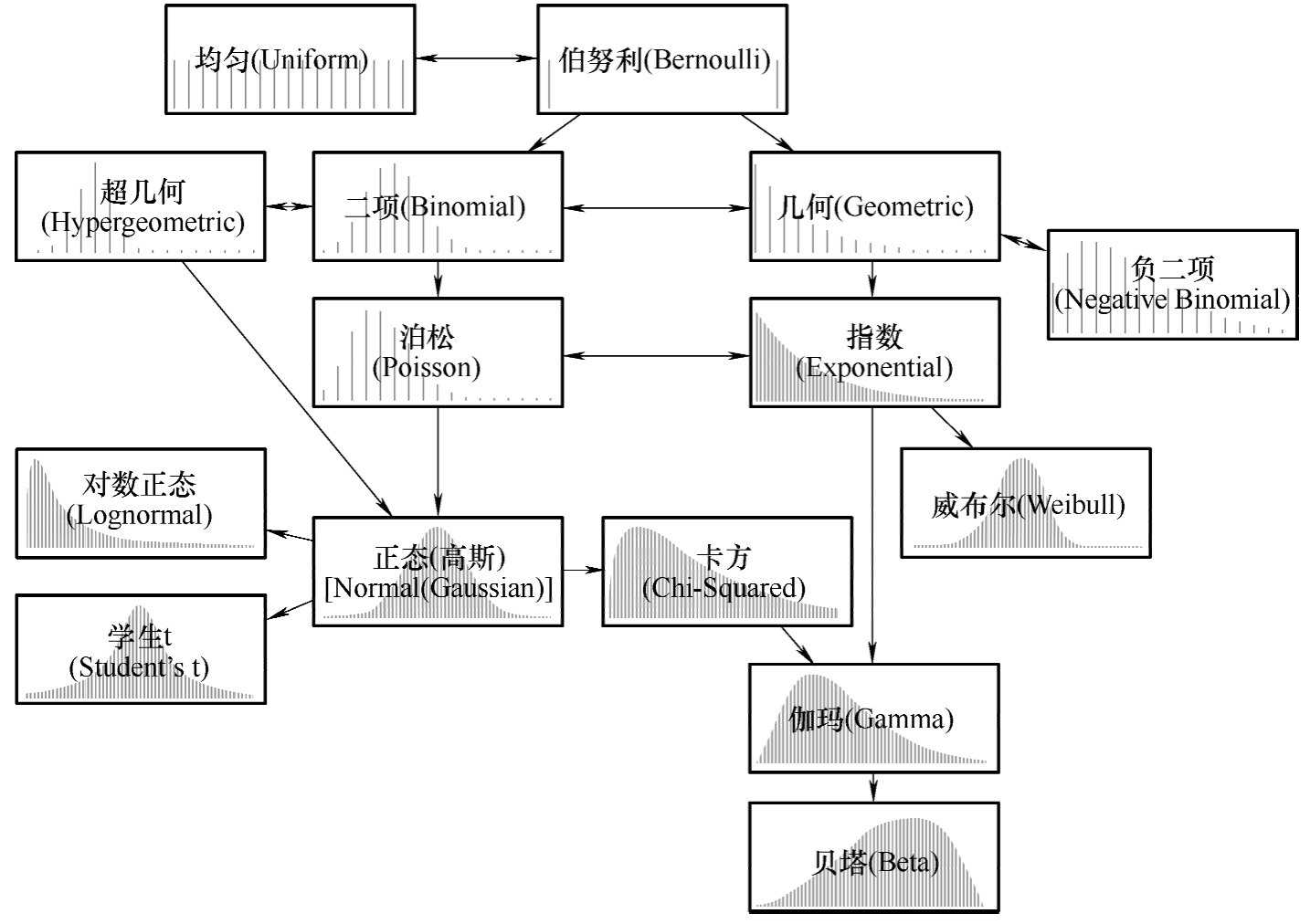
图3-4 常见的概率分布及其关系
1)数据离散还是连续;
2)数据分布是否对称,如果不对称,是正偏斜还是负偏斜;
3)数据是否有上下界,如风速不可能是负值、设备的时间稼动率不能大于1;
4)数据极端值的分布情况,如是正还是负,是否频繁出现。
参数估计是在抽样及抽样分布的基础上,根据样本统计量估计总体参数(例如均值、方差等)。参数估计方法包括点估计和区间估计,区间估计是在点估计的基础上,给出总体参数估计的置信区间,从而反映样本统计量与总体参数的接近程度。
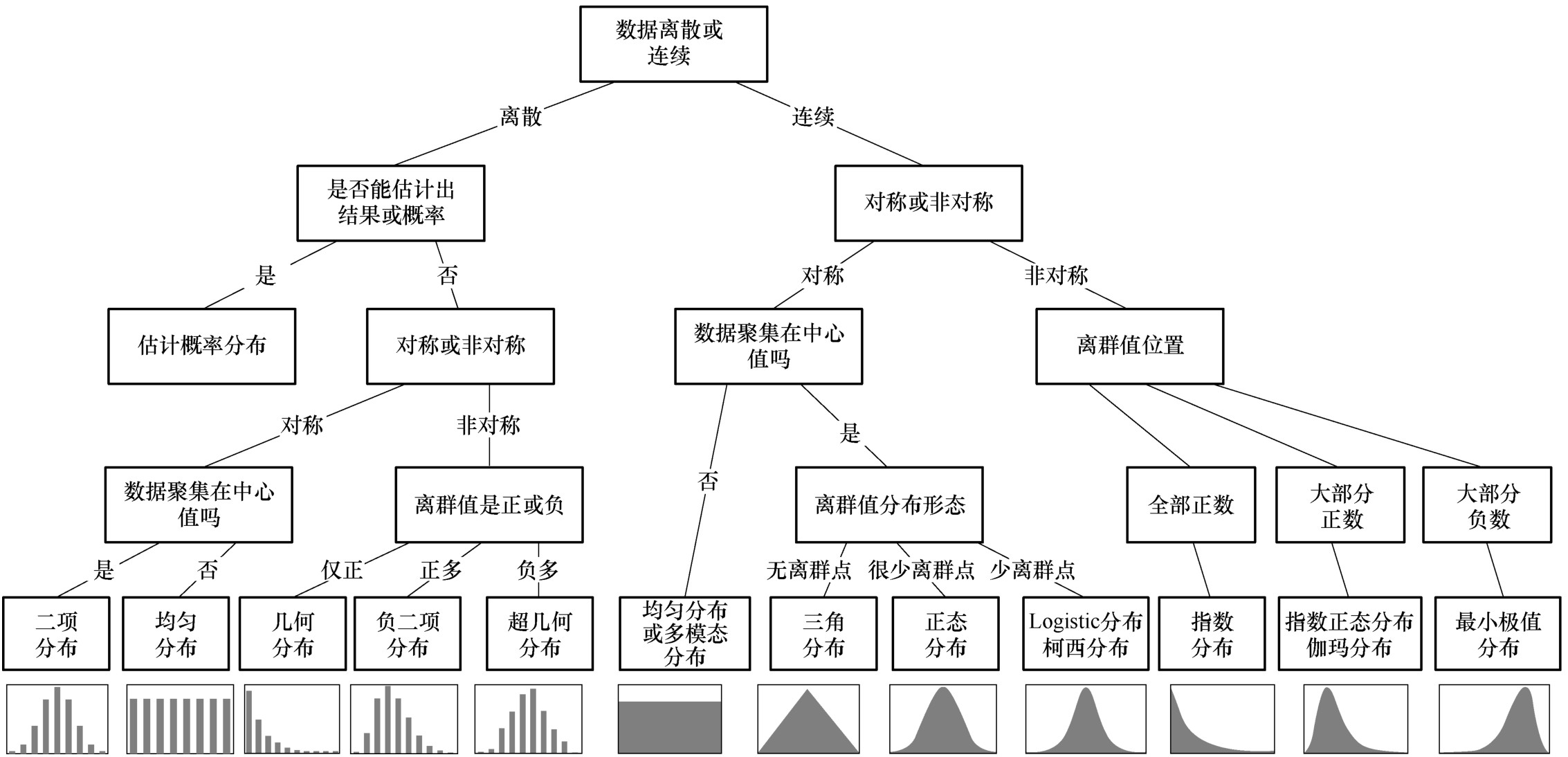
图3-5 概率分布判断流程
参数估计可以采用参数化模型,不同情形下的总体参数估计需使用不同的分布,单总体和双总体参数估计及其使用的分布如图3-6所示。
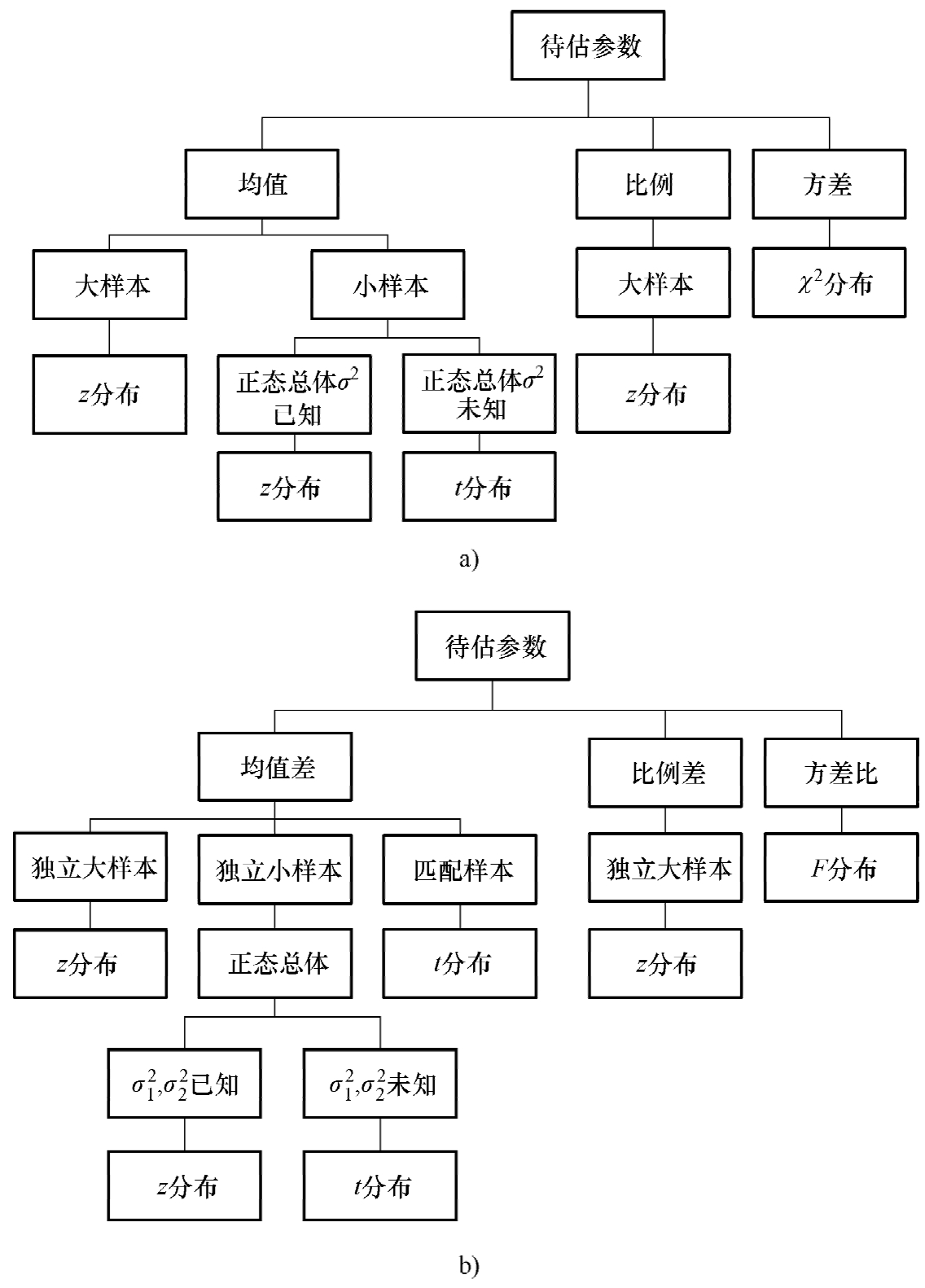
图3-6 单总体和双总体参数估计及其使用的分布
a)单总体 b)双总体
在非参数方法上,Bootstrap(自助法)、Jackknife(刀切法)等随机采样是参数估计的常用方法,基本思想很简单,将样本视为总体,在“总体”中不放回地抽取一些“样本”来做统计分析。Bootstrap、Jackknife都算是蒙特卡罗方法。假设原始数据集有 N 个样本,Jacknife就是每次都抽取 N -1个样本,也就是每次只剔除一个原样本,类似于“Leave one out”的交叉验证方法。Jackknife方法是有Maurice Quenouille在1949年提出的一种再抽样方法,其名字类比瑞士小折刀(很容易携带)。Bootstrap抽样方法从中有放回的随机抽样来评估总体特征,但一个样本可以被抽到多次。Bootstrap也分参数Bootstrap和非参数Bootstrap,前者的分布已完全知道。Bootstrap方法是Efron在1979年提出的,并论证Jackknife法是Bootstrap法的一阶近似(泰勒公式展开),在线性统计量估计方差问题上,两个方法等价。但在非线性统计量方差估计问题上,Bootstrap通常更有效。当统计量不太平滑(例如中位数)的时候,Jacknife有很大误差,而Bootstrap通常比较有效。Jackknife法计算效率通常更高。当样本量不大或者类别严重不均衡时,Bootstrap方法通常会失效。
在非参数化统计方面的更多内容可以阅读Wasserman的 All of nonparametric statistics [3] ,数值计算方法也可以参考Givens等人的《计算统计》 [4] 。R语言有resample、boot等算法包。
假设检验与参数估计都利用样本对总体进行某种推断,二者的主要区别在于,假设检验先对统计量的值提出某种假设,然后通过样本信息验证这个假设是否成立。假设检验的一般步骤如下:
1)先给出原假设 H 0 和与之对立的备择假设 H 1 ;
2)设定显著性水平 α ,通常取0.05或0.01;
3)根据样本数据计算检验统计量;
4)看统计量是否落入 α 下的拒绝域中,如果是则拒绝 H 0 ,反之则接受(无充分理由拒绝) H 0 。
假设检验按自变量与因变量类型的分类如表3-1所示 [5][6] ,直观解释请参阅参考文献[7]。
表3-1 假设检验按自变量与因变量类型的分类
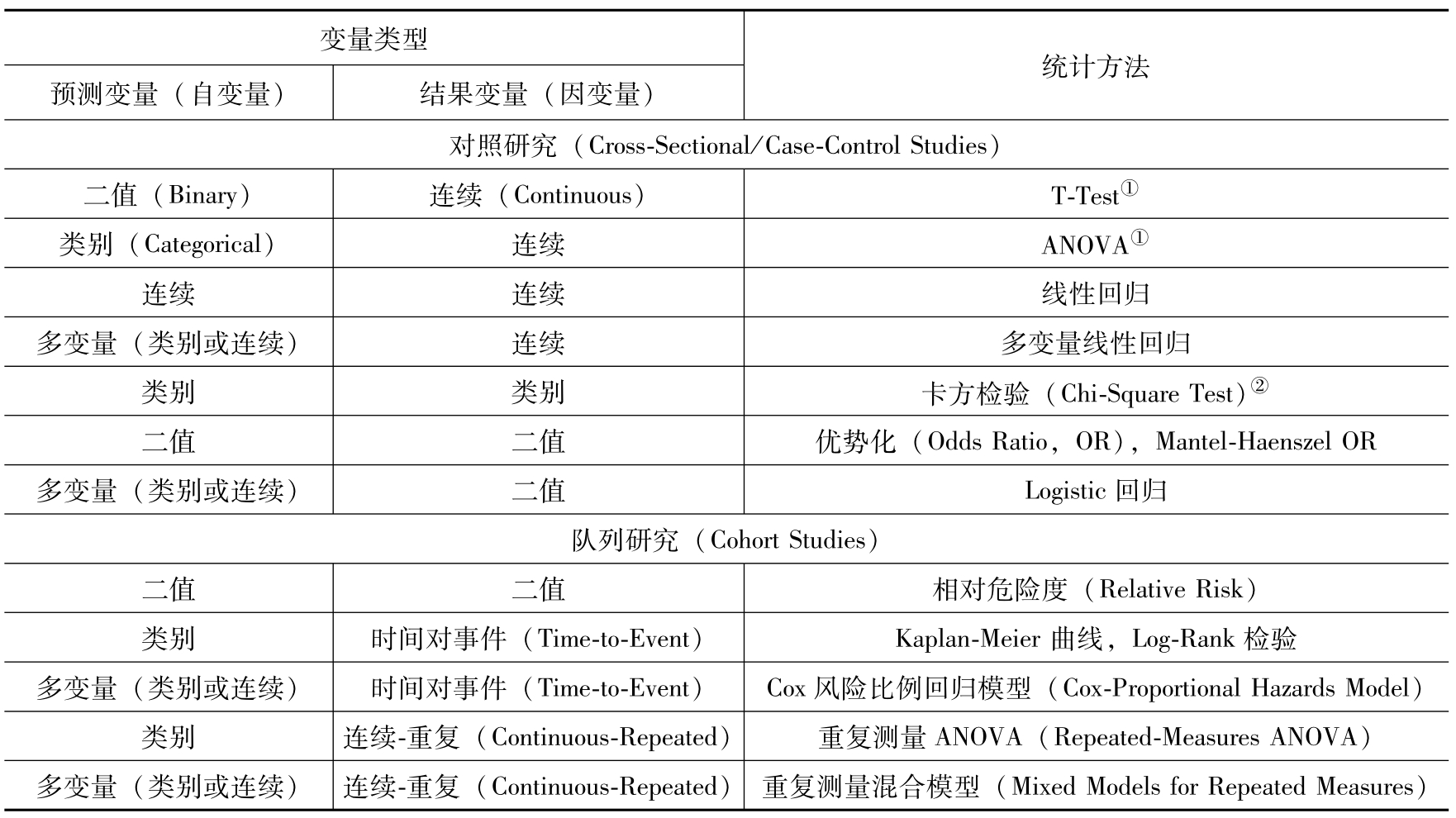
① 若结果变量明显不符合正态分布或样本量不足时,宜采用非参数化检验;
② 表示当组合单元(cell)中的预期样本少于5个时,宜采用费舍尔精确检验(Fisher Exact Test)。
按照总体分布是否已知,可以将假设检验分为参数检验和非参数检验,如图3-7所示。R语言的stats包提供了t.test(支持各种t检验)、wilcox.test(独立样本的Mann-Whitney检验、配对样本的Wilcoxon检验)、ks.test、shapiro.test(正态分布检验)、var.test(F检验)、chisq.test( χ 2 检验)、friedman.test等函数,Mood’s median检验在R语言的RVAideMemoire、coin包有提供。
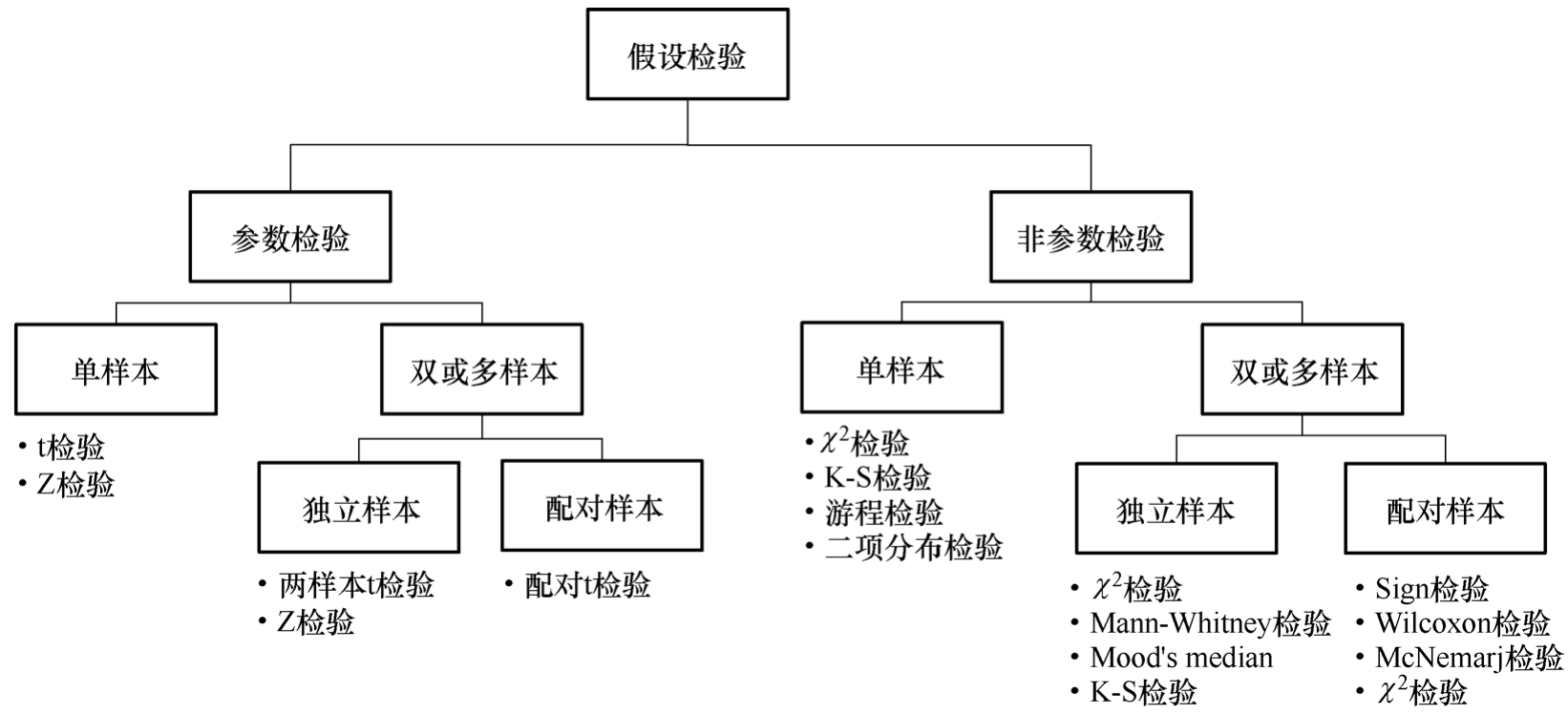
图3-7 参数检验和非参数检验