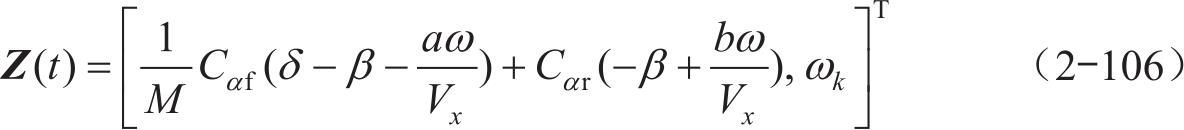2.3.4 基于UKF的横摆角速度及质心侧偏角的联合估算

无损卡尔曼滤波（Unscented Kalman Filter, UKF）以无损变换（Unscented Transform, UT）为核心，利用高斯分布的特点，从原始状态中取一些特定的点来获取对应的原始状态高斯分布特性，传递更准确的均值和协方差。当目标对象的非线性程度提高到一定水平的时候，UKF将拥有更高的精度，且不需要对系统线性化，运算过程中不需要计算系统的雅克布矩阵，可以提高估算的效率和稳定性。非线性系统的状态方程如下：

观测方程：

UKF流程如下：

（1）初始化

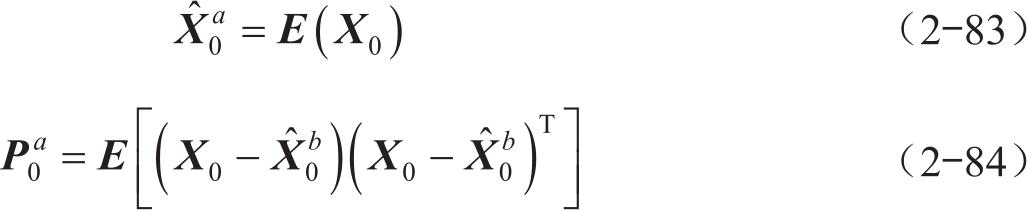
（2）时间更新部分

1）生成2 n 个sigma采样点，采样点来源于原始状态附近，进行适当的运算得到。

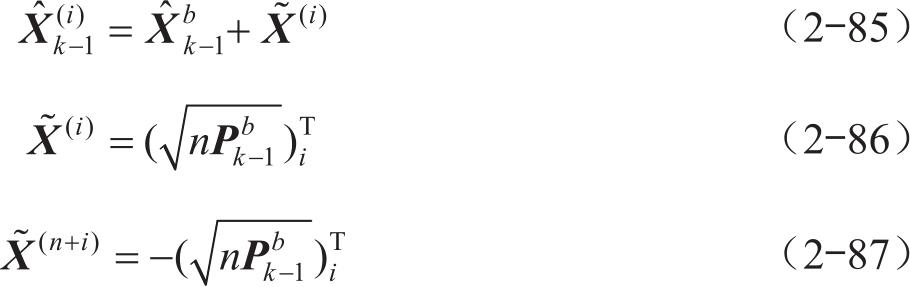
2）将各个采样点代入状态方程，可以得到：

3）计算得到 k 时刻的均值：

4）计算得到 k 时刻的协方差：

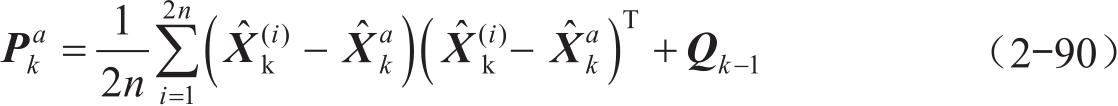
（3）观测更新部分

1）根据预测值，重新生成一批采样点。

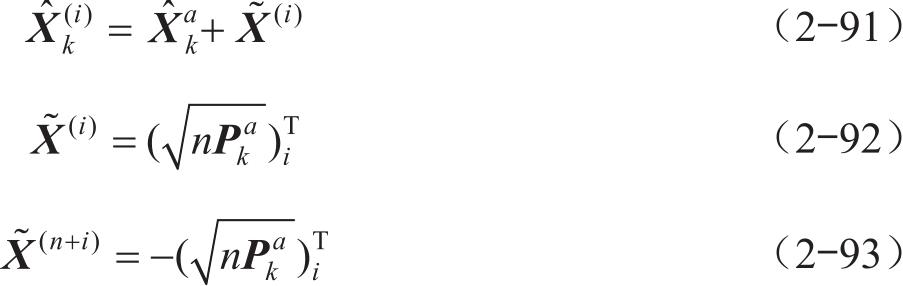
2）将各采样点代入观测方程，可以得到：

3）计算得到 k 时刻的均值：

4）计算得到 k 时刻的协方差：

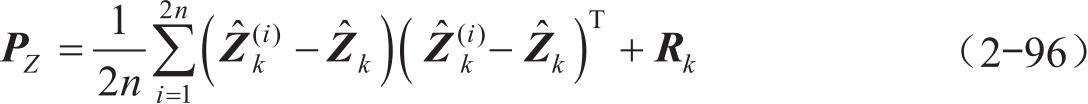
5）估计状态和观测之间的协方差：

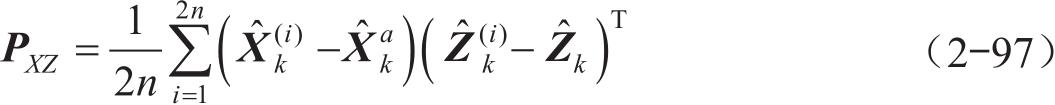
6）最终利用卡尔曼增益更新状态量：

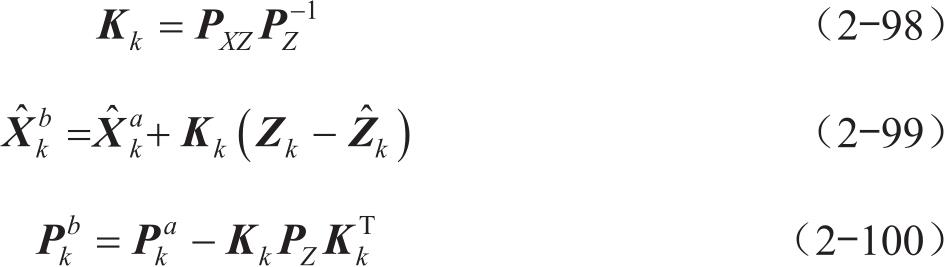
结合UKF的流程，设计一个质心侧偏角 β 和横摆角速度 ω 的状态估算器。估算状态量质心侧偏角 β 和横摆角速度 ω ，写成向量的形式：

观测变量横向加速度 A _y 、横摆角速度 ω ，写成向量的形式：

外界输入的影响变量方向盘转角 δ ，写成向量的形式：

状态方程如下：

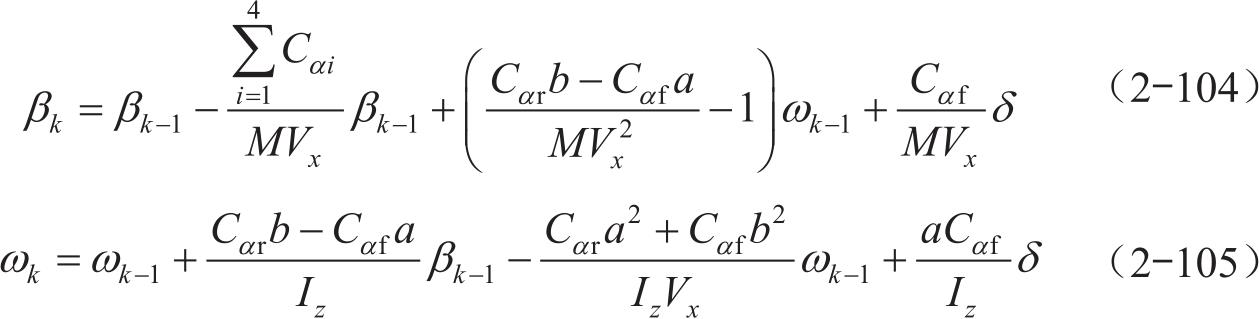
观测方程如下： 2Pb+u9LYWEoxRqJeQBk5Yyay4qEjY0diiGulVV4Envq+w7N03CLzaAdFkyrSjnpx