




整车质量和道路坡度等参数会影响车辆各轴和各轮的载荷情况,进而影响到驱动力和制动力的分配和控制,对操纵稳定性和经济性有较大的影响,是重要的车辆参数和分布式驱动控制的重要输入。因此,根据整车纵向受力情况实时估算整车质量及道路坡度,有助于分布式驱动控制策略设计。通常认为在车辆起步后,质量不再发生变化,因此只需要在每次车辆起步后的一段稳定行驶时间内,对整车质量进行估算即可,不需要长时间估算,以免增大运算量和估算误差。
系统参数估计是通过先验知识建立一定的数学模型,并根据某种准则来处理系统的输入和输出,估算某些重要的系统参数。根据车辆纵向动力学分析,通过递推最小二乘法估算整车质量。最小二乘法在参数估算领域是非常常见的一种算法,它本质上是估算出系统参数,使被估算参数参与的系统输入输出与实际系统中的输入输出的平方和差距最小,估算结果可呈现一定的统计规律。这种算法相对简单,易于实现,且计算性能好。递推最小二乘法可以不断对已经获取的参数补充新的数据,具备一定的实时性,可进行参数在线估计。
第2.2.1节和第2.2.2节已经在车辆纵向上建立了驱动及制动的动力学模型,表明了车辆在运动过程中的受力情况,将输入量驱动力/制动力与输出量加速度/减速度联系起来,整车质量及坡度作为待识别的参数,已经转换为最小二乘法的基本形式。
在第2.2.1节驱动动力学模型分析中,最小二乘法的基本形式即式(2-9)中 y 为系统输出变量, ϕ T 为系统输入变量, θ 为待识别的参数(包含整车质量及坡度)。
设定
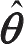 为参数的估计值,当估算出准确的数值时,可以使得准则函数(误差函数)最小。误差函数可表示为
为参数的估计值,当估算出准确的数值时,可以使得准则函数(误差函数)最小。误差函数可表示为
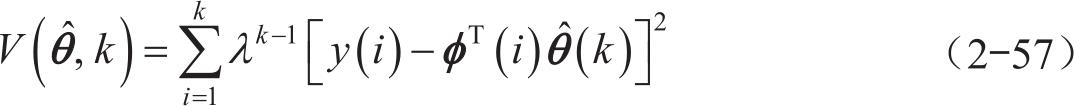
式中, λ 为遗忘因子,一般取值范围为0~1。当 λ 取0时,完全抛弃历史结果,估计结果只与最新结果有关;当0< λ <1时,遗忘因子淡化历史结果对估计结果的影响,值越小,淡化作用越强;当 λ =1时,遗忘因子不起作用;当 λ >1时,遗忘因子加强历史结果对估算结果的影响,淡化新数据对估算结果的影响。
根据递推最小二乘法的定义和推导,可以得到 k 时刻的参数估计值为
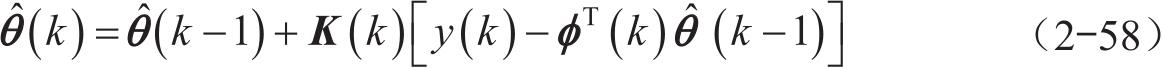
其中 K (k) 为增益矩阵,其具体公式为
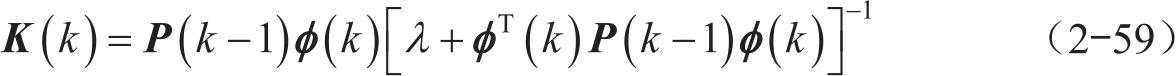
P (k) 为协方差矩阵,其具体公式为
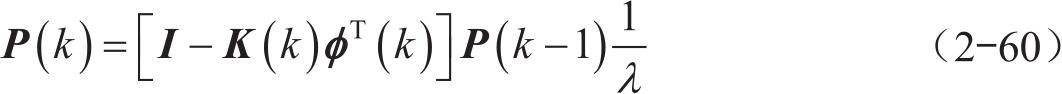
由于这个系统中有整车质量和坡度两个需要估计的参数,且两者的变化规律不一样。一般车辆行驶过程中,整车质量几乎没有变化,而坡度可能有较频繁的变化,那么使用单一遗忘因子将会导致不适合某一参数的估算,从而使整个系统的参数估算都出现偏差。为了解决不同参数变化速率不同,使用同一遗忘因子误差较大的问题,需要多遗忘因子来对应不同的参数。
当引入多遗忘因子后,误差函数可表示为
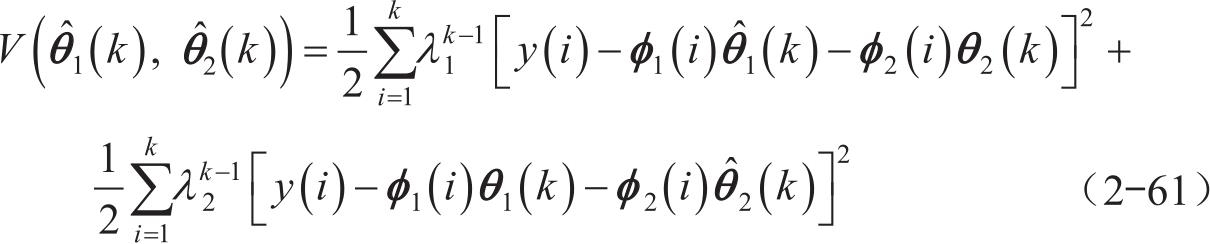
式中, λ 1 为第一个参数的遗忘因子; λ 2 为第二个参数的遗忘因子。
两个不同的遗忘因子分别对两个变化速率不同的参数进行调节,更加符合系统规律,使得误差函数可以达到最小值。式(2-61)对待估计参数求偏导为0并整理可得
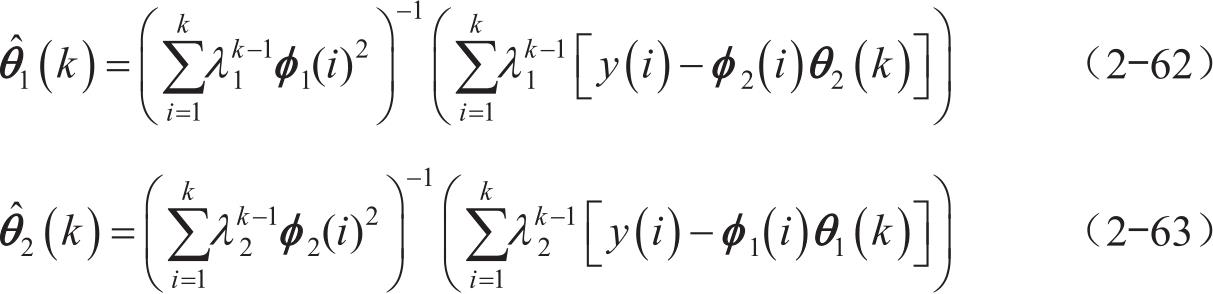
对式(2-62)和式(2-63)进行计算并整理可得到以下两个递推公式:
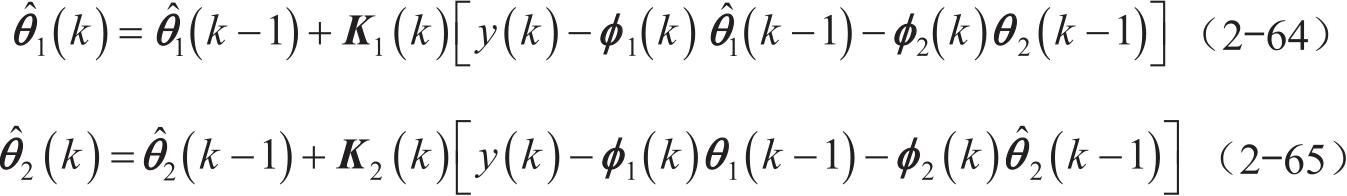
式(2-64)和式(2-65)中的增益矩阵及协方差矩阵分别如下:
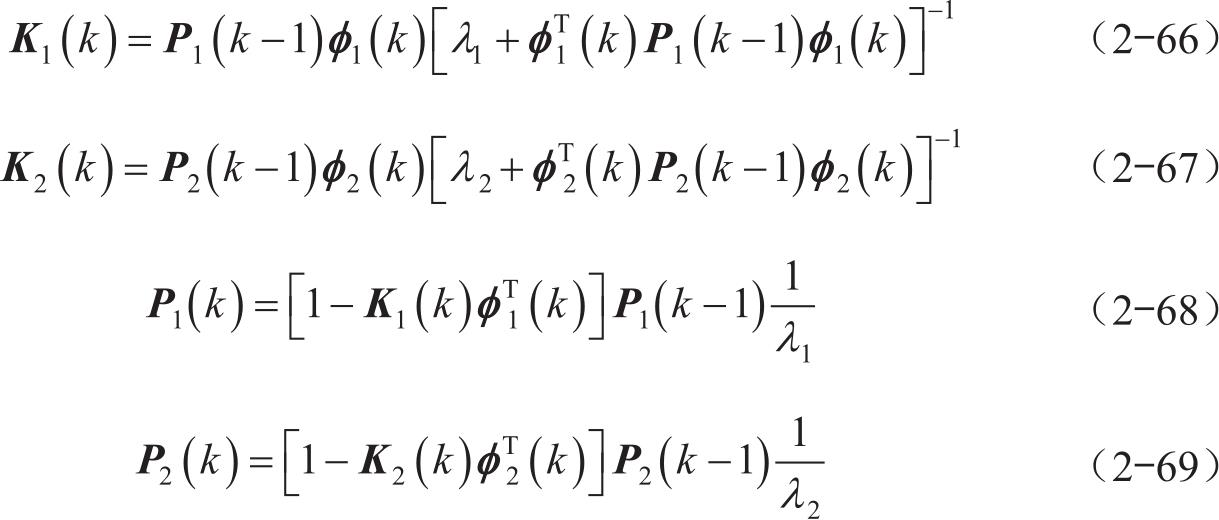
将式(2-64)和式(2-65)中的真实值替换成估计值,可以得到以下结果:
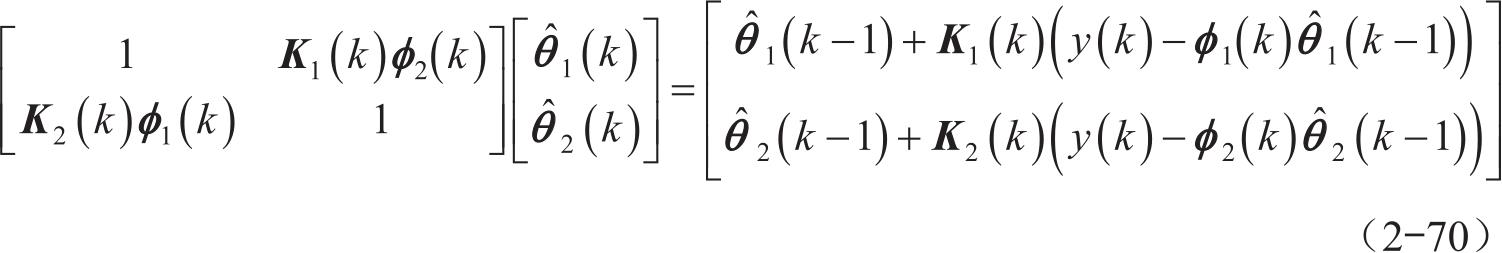
对式(2-70)进行求解并整理,可以得到递推的最小二乘法的基本形式如下:
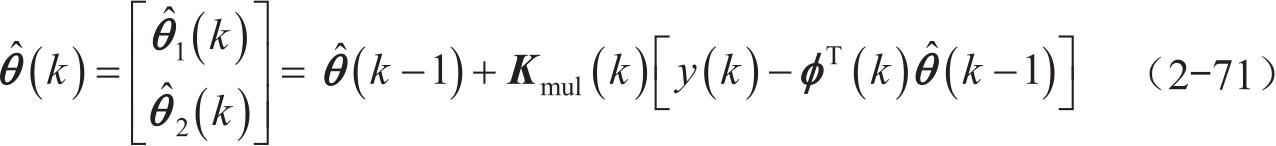
其中,有多遗忘因子影响的增益矩阵为
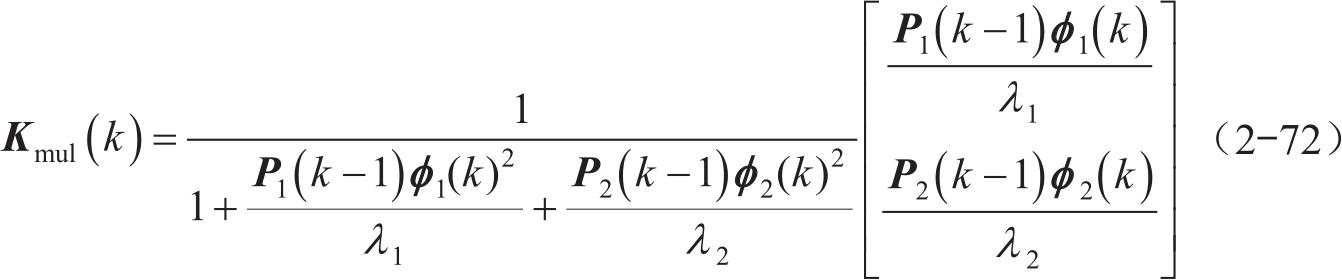
此时,多遗忘因子可以分别对所对应的参数进行独立调节以适应不同参数不同的变化速率。
多遗忘因子的引入解决了不同参数变化速率不同的问题,但是遗忘因子仍然是固定的,对参数估计的影响效果也是固定的。然而在估计的初始阶段,参数估计值会与真实值存在较大的误差,此时我们需要更多的数据参与到参数估计当中,让新数据产生更多的作用,因此需要较小的遗忘因子来淡化历史数据的影响;进入估计的后期,参数估计值与真实值的误差会缩小,此时需要更稳定的估计值,避免不良的新数据产生影响。
因此,相关学者提出了一种变化的遗忘因子取值方法,采用基本函数使得遗忘因子取值逐渐增大,最终趋近于零。公式如下:

该遗忘因子随时间变化曲线如图2-9所示。本书中整车质量这个参数符合上述特征,将采用式(2-73)表示的遗忘因子作为第一个遗忘因子 λ 1 ,第二个参数坡度采用固定遗忘因子 λ 2 ,即采用带可变多遗忘因子的递推最小二乘法对整车质量及坡度进行联合估算。
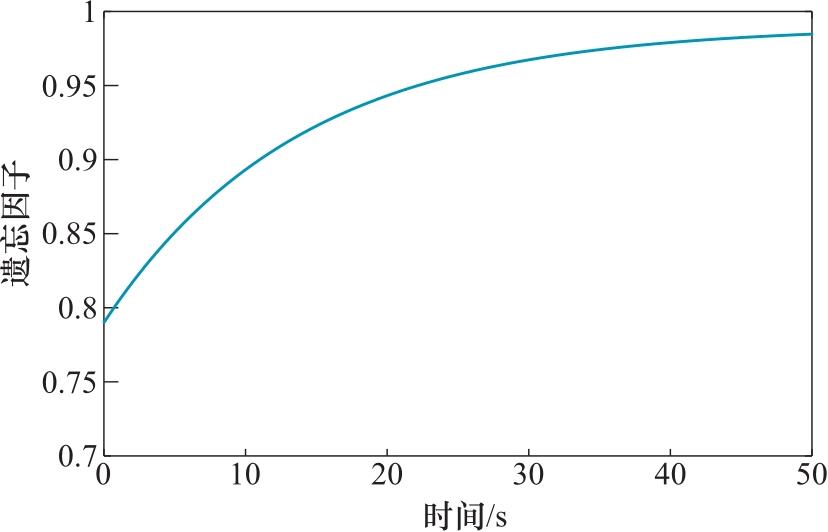
图2-9 可变遗忘因子变化曲线