




市场参与者、政策制定者以及(如美联储一样负有系统性风险监管职责的)监管者面临的艰巨任务,是找到一个办法,既能控制金融市场相互关联带来的潜在副作用,又能维护其好处。
——珍妮特·耶伦(Janet Yellen,2013)
随着国际贸易的增长,国际金融在过去几十年中也急剧增长。例如,全球外资投资额已从2000年的26万亿美元上升至2016年的132万亿美元,超过全球投资总额的三分之一(Lund and Härle,2017)。此外,金融部门之间的相互依赖也逐步增强,资金不仅在不同国家之间流通,也在不同金融机构之间流通。杜阿尔特和琼斯(Duarte and Jones,2017)基于美联储的监管数据,估算出银行控股公司23%的资产以及48%(近一半)的负债来自美国金融体系内部。
全球化以及与之关联的范围经济和规模经济带来了巨大的和平与繁荣红利。然而,随着金融网络联系的日趋密切,网络节点也越来越大,这为可能的系统性风险埋下了隐患。金融机构之间的相互依赖关系起到了“放大器”的作用,提供了将金融体系某部分的初始冲击广泛传播的渠道,导致最终损失远远超出基本面的初始变化。上述情况并非杞人忧天,正如2008年我们见到的,抵押贷款市场的初始问题逐步导致美国及其他地区的一些重大破产事件,最终引发了全球金融危机和持久的衰退。

由于金融机构以多种方式相互依赖,金融市场充斥着外部性。从最基础的层面看,如果任其蔓延,破产带来的大量损失会通过违约和股权减值渠道继续传播。外部性显而易见:如果某家机构投资判断失误、经营管理不善甚至只是异常的运气不佳,最终都会影响其合作伙伴的价值,并进一步影响合作伙伴的合作伙伴,这一系列传播是以非连续的方式发生的。金融网络中还存在许多其他形式的外部性,包括银行挤兑、低价抛售导致的资产价值变化、投资者根据某一家机构的状况推断另一家机构的状况,以及信贷冻结等。
 尽管其中的部分风险可被对冲,但目前还有很多风险并无对应的市场来防范。外部性意味着金融体系作为一个整体,可能经历远比引发危机的独立失灵事件范围更广、代价更大的危机,“系统性风险”的概念因此产生。
尽管其中的部分风险可被对冲,但目前还有很多风险并无对应的市场来防范。外部性意味着金融体系作为一个整体,可能经历远比引发危机的独立失灵事件范围更广、代价更大的危机,“系统性风险”的概念因此产生。
实际上,许多形式的系统性风险可通过适当的监督和干预来降低甚至完全避免。然而,这需要对金融网络的相互依赖关系有全面细致的认识,对网络节点上各方的激励以及可能产生的关联结果有深刻的理解。这些都是本文关注的重点。
在过去几十年中,关于金融网络关系的研究日益增多,为本文更好地理解系统性风险提供了帮助。
 本文构建了金融网络和系统性风险之间关系的理论框架。首先,区分了两种类型的系统性风险:(1)通过多种渠道的传染,这些传染在金融机构之间形成外部性(如违约、相互关联的投资组合、低价抛售等);(2)自我实现的预言和反馈效应(如银行挤兑、信贷冻结、多重均衡等)。其次,探讨每种风险如何取决于互相依赖的网络。最后,基于上述分类方法,研究银行选择其投资和合作伙伴的激励对系统性风险的影响、系统性风险和金融中心度(financial centrality)的度量以及干预或监管的时机和举措。
本文构建了金融网络和系统性风险之间关系的理论框架。首先,区分了两种类型的系统性风险:(1)通过多种渠道的传染,这些传染在金融机构之间形成外部性(如违约、相互关联的投资组合、低价抛售等);(2)自我实现的预言和反馈效应(如银行挤兑、信贷冻结、多重均衡等)。其次,探讨每种风险如何取决于互相依赖的网络。最后,基于上述分类方法,研究银行选择其投资和合作伙伴的激励对系统性风险的影响、系统性风险和金融中心度(financial centrality)的度量以及干预或监管的时机和举措。
实证分析的相关背景、金融网络的相关资料以及本综述的概要收录在在线补充附录中。
在金融世界里,违约和金融危机的历史与投资一样久远:从公元33年提比略大帝治下的信贷大紧缩,到拿破仑战争时期许多国家一再出现的外部违约,再到19世纪反复出现的银行挤兑和恐慌。此类危机爆发和终结方式的多样性(Reinhart and Rogoff,2009),需要对引发系统性问题的外部性进行分类。
本文提出了一种两层分类法。第一层,首先区分两种类型的系统性风险:(1)通过直接外部性造成的传染(例如,一家银行违约给另一家银行造成压力,或一家银行的资产抛售导致另一家银行的价值下降);以及(2)形成多重均衡和自我实现预言的各种反馈效应(例如,“认为某家银行可能状况不佳,引发投资者收回贷款,最终导致该银行真的状况不佳”这样的预言自我实现)。第二层,进一步区分每种系统性风险的不同作用方式。在进行第二层分类之前,本文先探讨不同情景下金融网络的构成。
金融网络是许多机构以各种方式相互关联的复杂系统。第一,各机构通过金融合约相互关联。机构之间通过相互借贷平滑特殊的流动性变化,满足保证金要求(deposit requirements);在投资机会上共同合作;以链条(chains)的形式相互对资产再包装和转售。上述相互依赖的网络是大部分现有文献关注的焦点(例如,Allen and Gale,2000;Eisenberg and Noe,2001;Elliott et al.,2014)。
第二,即使金融机构之间没有直接交易,共同的风险敞口也会导致其价值的相关性。这可以通过金融网络来追踪。在金融网络中,两家机构之间的(加权)连接(weighted link)可以刻画其投资组合之间的相关性(Acharya and Yorulmazer,2007;Allen et al.,2012;Diebold and Yilmaz,2014;Cabrales et al.,2017)。
也有越来越多的文献将不同形式的相互依赖关系联系在一起。有研究(Heipertz et al,2019)显示,银行在外部和银行间交易资产,价格会调整至市场出清。金融网络是均衡状态下银行间权益价值关系的简化形式:在给定交易和价格诱导型转移(induced shifts)时,金融机构i到金融机构j的加权连边(weighted edge)描述了i价值下降对j价值产生影响的局部均衡效应。
尽管金融网络的性质因模型而异,但所有模型都强调了同样的事实:金融的相互依赖会产生系统性风险。因此,规范的金融网络模型有助于衡量、预测和追踪系统性风险的来源。由此,本文引入了一个涵盖许多文献的研究框架,使我们可以区分两种类型的系统性风险。
假设有一组金融机构N={1,…,n}。本文称之为银行,但实际上应被更广泛地理解为金融体系中任何会相互影响的机构。
该金融网络由矩阵G=(g
ij
)
ij
刻画,其中g
ij
表示银行i和银行j之间的连接。连接g
ij
可包含多个组成部分,例如,每一个组成部分对应一种不同类型的金融合约。

本文最感兴趣的关键对象是与每个机构相关的价值向量V=(V i ) i ,该向量表示所有的资产和负债,包括任何违约和与之相关的破产成本。由于银行是相互关联的,因此它们的价值也相互依赖。银行i的价值是其他银行价值的函数,用V i =F i (V|G)表示。银行价值是包含n个未知数的n个方程组的解,表示为:

在某些条件下,特别是F(·|G)非减且在V中有界时, [1] 根据塔尔斯基不动点定理(Tarski's fixed point theorem),可知方程(1)存在均衡解,即其一致的值。因此,“均衡”一词仅指一致计算(coherent accounting),而不是指最优反应或某些动态系统的不动点。这里可能存在多重均衡,而这些均衡的集合形成一个完全格(complete lattice):完全格中存在最大均衡和最小均衡,分别对应所有机构同时达到的最高和最低可能均衡值,在下文中我们称之为最好均衡和最坏均衡。 [2]
我们区分了由银行间相互依赖产生的两种系统性风险来源。首先,银行i价值的变化会影响银行j,银行j价值的变化用
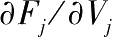 表示。银行j价值的变化进一步影响与银行j相关联的银行的价值,以此类推:一家银行价值的变化会通过网络传播并产生深远影响。这一形式的风险是许多金融传染研究关注的焦点。第二种类型的系统性风险源于均衡的多重性以及从一种均衡到另一种均衡的可能转移。即使基础投资价值未有任何变化,网络相互依赖也能导致自我实现的反馈效应,使信念的变化成为现实。因此,第一种类型的系统性风险反映了基本面变化如何通过网络传导,形式化地说,就是在保持均衡状态不变的情况下,作为对基本面初始变化的回应,均衡值V会发生多大的变化。而第二种类型的系统性风险反映了均衡状态之间的转移。
表示。银行j价值的变化进一步影响与银行j相关联的银行的价值,以此类推:一家银行价值的变化会通过网络传播并产生深远影响。这一形式的风险是许多金融传染研究关注的焦点。第二种类型的系统性风险源于均衡的多重性以及从一种均衡到另一种均衡的可能转移。即使基础投资价值未有任何变化,网络相互依赖也能导致自我实现的反馈效应,使信念的变化成为现实。因此,第一种类型的系统性风险反映了基本面变化如何通过网络传导,形式化地说,就是在保持均衡状态不变的情况下,作为对基本面初始变化的回应,均衡值V会发生多大的变化。而第二种类型的系统性风险反映了均衡状态之间的转移。
 一场基于传染的危机是由基本面变化引发的,但触发均衡状态发生转移的因素可能更加模糊。对金融网络来说,均衡状态的转移通常可能是市场冻结,而市场冻结很可能是由不确定性加大驱动的,即不确定性加大导致银行和其他机构对其交易对手的信任度降低。
一场基于传染的危机是由基本面变化引发的,但触发均衡状态发生转移的因素可能更加模糊。对金融网络来说,均衡状态的转移通常可能是市场冻结,而市场冻结很可能是由不确定性加大驱动的,即不确定性加大导致银行和其他机构对其交易对手的信任度降低。
本文的其余部分将讨论这两种不同形式的系统性风险,并指出与之相应的外部性和导致效率低下的市场缺陷。
本小节讨论危机经由交易对手风险和共同的风险敞口直接传导。
传染的一种典型方式是连锁破产。一家银行的投资回报率过低,导致其无法偿还债务。随着这家银行对债务违约,其他机构的资产负债表恶化,最终导致部分机构破产。随着越来越多的机构破产,其他机构的价值进一步下降,破产通过金融网络蔓延开来。
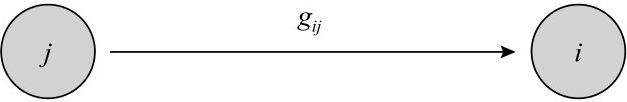
图1 银行j欠银行i规模为g ij 的债务
如图1所示,两家银行的关系代表一项债权:g ij 表示银行j欠银行i的债务D ij ,箭头表示价值流动的方向。在本例中g ij =D ij 。银行间合约使得银行(账面)价值之间形成了相互依赖,即:
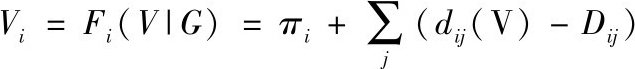
其中π
i
是银行i的外部投资组合的价值,
 d
ij
(V)是银行j能够成功支付给银行i的金额,由于有限债务责任,此项债务的价值等于:
d
ij
(V)是银行j能够成功支付给银行i的金额,由于有限债务责任,此项债务的价值等于:
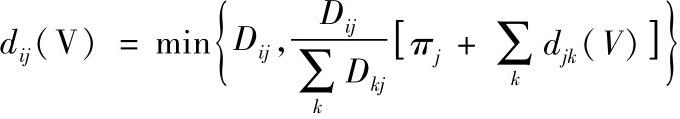
为简单起见,本文假设所有债务的优先级相同。其中
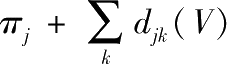 是银行现在能用于支付债务的价值,并根据债权人对银行j的债权比例分配。在更一般的情况下,该函数应该是反映债务优先级的嵌套函数(nested function)。
是银行现在能用于支付债务的价值,并根据债权人对银行j的债权比例分配。在更一般的情况下,该函数应该是反映债务优先级的嵌套函数(nested function)。
为了解相互依赖性如何产生系统性风险,让D ij =1、π i =0.5,并假设银行j的外部投资组合价值从π j =1.5降至π′ j =0.5。在π下,两家银行的初始价值分别为V i =1.5和V j =0.5,但在π′下,价值分别降至V i =1和V j =-0.5(或在有限债务责任下实际为0)。虽然冲击直接影响银行j的投资组合,但也会使银行i的价值降低。进一步地,如果银行i与其他机构存在债务关系,其价值的降低就可能会导致自身违约。
这种连锁反应不会导致除投资组合价值下跌以外的额外损失。然而,到目前为止,我们忽略了破产会涉及大量破产成本这一事实。例如,破产成本增加0.5,将导致在π′下银行价值分别降至V i =0.5和V j =-1。每多一家机构破产都会给整个体系带来额外损失,导致总成本大大超出初始冲击。损失还包括破产银行的一些投资和贷款业务。
早期的交易对手风险模型主要由罗歇和梯若尔(Rochet and Tirole,1996)以及艾伦和盖尔(Allen and Gale,2000)创建,这些模型对银行和储户的行为建模。例如,艾伦和盖尔(2000)研究了受到流动性冲击的银行(例如,预期外的提款)。为防范冲击,银行可以事先互换部分存款。在无总体不确定性(aggregate uncertainty)的情况下,通过整个交叉存款网络,可以实现跨银行债权的最优配置。需要早期流动性的银行可从流动性过剩的银行获得流动性。然而,一旦发生预期外的冲击或多家银行同时受到冲击,又或者网络出现连接不当,上述债权关系就会导致金融不稳定和传染。接着,一家银行从另一家银行抽取流动性会导致流动性不足的情况蔓延。
有研究(Eisenberg and Noe,2001)提出了一种算法,用来计算银行间债务责任网络中银行间的均衡支付。该算法遵循违约链,当旧的违约不再引发新的违约时算法终止。近期的一些文献研究了其他类型的银行间金融合约,比如股权(Elliott et al.,2014)。股权也使银行的市场价值相互依赖:银行投资组合的下跌使其自身价值下降,进而压低其股权持有人的价值,并进一步影响股权持有人的股权持有人的价值,以此类推。
 此类模型已扩展到不仅包括债务,还包括权益(Jackson and Pernoud,2019)。与债务合约相比,权益类合约的相互依赖对系统性风险的影响不同,因为它们可以使银行在不违约的情况下助长系统性风险的传染。例如,如果银行2持有银行1的股票,即使银行1有偿付能力,银行1的价值下跌也会使银行2的价值下降,这可能导致银行2破产并产生破产成本,进而造成银行2的债权人违约,特别是在他们也持有银行1的股票、财务上已经较为脆弱的情况下。因此,股权价值下跌、债务违约和共同的风险敞口三者叠加,可能导致链条式违约。
此类模型已扩展到不仅包括债务,还包括权益(Jackson and Pernoud,2019)。与债务合约相比,权益类合约的相互依赖对系统性风险的影响不同,因为它们可以使银行在不违约的情况下助长系统性风险的传染。例如,如果银行2持有银行1的股票,即使银行1有偿付能力,银行1的价值下跌也会使银行2的价值下降,这可能导致银行2破产并产生破产成本,进而造成银行2的债权人违约,特别是在他们也持有银行1的股票、财务上已经较为脆弱的情况下。因此,股权价值下跌、债务违约和共同的风险敞口三者叠加,可能导致链条式违约。
因为受影响的机构无法完全对冲风险,所以一家机构的投资决策会影响自身的债务偿付能力和其他机构投资组合的回报,这种外部性导致了无效率。考虑到破产涉及破产成本以及其他成本,这些并不是一家机构到另一家机构的简单价值转移。
另一种形式的传染不那么直接,它来自资产价格的外部性。当一家银行出现破产危机时,它通常不得不提前出售大量资产,即所谓的低价抛售。抛售压低了资产的价格,也拉低了其他银行持有类似资产的组合的价值。这可能导致其他银行违约,并使资产出售陷入螺旋式下跌的漩涡(Kiyotaki and Moore,1997;Cifuentes et al.,2005;Gai and Kapadia,2010;Capponi and Larsson,2015;Greenwood et al.,2015)。当银行间的投资组合相互关联时,这一问题尤为严重。不仅由于多家银行同时遭遇共同的风险敞口而导致情形更为危险,而且在由此导致的低价抛售中价格也面临更大的下行压力。
低价抛售对市场价格的影响取决于以下几个市场缺陷。首先是金融市场深度不够,无法吸收大型银行资产组合清算导致的价格冲击。同时,也可能存在信息不对称,市场参与者在观测到大规模的资产出售时,可能会推断某些与基本面相关的情况。因此,市场价格下跌可能会放大初始冲击,尤其是在一个许多资产以市价计价、存在信息不对称和大型机构的金融体系中。
重要的是,由于银行间风险敞口的共性,基于价格的传染可能加剧连锁破产。这里我们可以观察到,在投资中有相似风险敞口的两个交易对手之间存在三个层面的相互影响。首先,它们往往同时处于脆弱和濒临破产的状态。其次,如果一方被迫出售部分资产,那么价格效应会损害另一方的资产负债表。再次,如果一方对另一方违约,后者就可能陷入破产危机,尤其是考虑到前两种相互影响,这意味着这家银行已陷入困境。虽然单有直接违约冲击、共同风险敞口或间接价格影响,并不一定导致进一步的破产,但这三种效应的叠加就会导致连锁反应。例如,相关研究(Cifuentes et al.,2005;Gai and Kapadia,2010)的模拟结果揭示了由交易对手风险产生的传染如何通过低价抛售被放大。他们研究的金融网络中包含两种类型的银行间联系:(1)资产负债表债务和(2)当某银行被迫对投资组合去杠杆化时的价格效应。他们进一步研究了传染风险如何取决于银行间债务的网络结构,特别是密度。
 这不仅仅是理论上的关注,因为有证据显示,如果两家银行的投资组合相关性更强,它们也更有可能成为交易对手(Elliott et al.,2018),这表明,通过金融债务关联的银行往往会基于风险敞口的共性更密切地关联。
这不仅仅是理论上的关注,因为有证据显示,如果两家银行的投资组合相关性更强,它们也更有可能成为交易对手(Elliott et al.,2018),这表明,通过金融债务关联的银行往往会基于风险敞口的共性更密切地关联。
共同的风险敞口为另一种形式的传染埋下了隐患:相似之“罪”。对于与已破产机构类似的机构,其偿付能力会受到质疑。
 两个关键因素使这种传染成为可能:(1)银行间的相关投资组合,(2)基本面价值和/或银行投资组合结构的不确定性。
两个关键因素使这种传染成为可能:(1)银行间的相关投资组合,(2)基本面价值和/或银行投资组合结构的不确定性。
为阐明上述观点,假设有k=1,…,K项原始资产,每项资产的独立价值为p k 。银行i的投资组合由其对不同资产的投资q i =(q ik ) k 唯一刻画。为了隔离推断效应(inference effect),假设银行之间没有合约:每家银行的全部价值都基于其自身的原始资产投资组合。本例中的(无方向)金融网络刻画了资产持有的相关性,即g ij =∑ k q ik q jk σ k 2 ,且有σ k 2 =Var(p k )。即使投资者不能直接观察到银行不同资产或投资组合的实现价值,因此他们也不能确定q i 或p k 的值,银行的均衡市场价值也应该是一致的,而且满足:
对于所有i,有
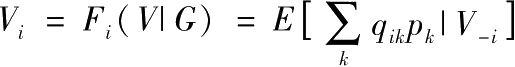
再看图1中的网络,并假设有两项外部资产,其收益分别为p A 和p B 。首先,假设银行2的全部投资组合都投资于资产A,银行1的投资组合在这两种资产上平均分配,上述投资情况为投资者所知。在事先没有任何额外信息的情况下,每家银行的价值就应该等于其投资组合的无条件预期价值:V 1 =E[0.5(p A +p B )]=0.5(μ A +μ B )以及V 2 =μ A 。现在考虑如果披露银行1的价值将低于预期,即0.5(p A +p B )=X<0.5(μ A +μ B )会发生什么。接着,考虑资产持有的重叠,投资者会更新其对银行2的估值至V 2 =μ A -2σ A 2 (σ A 2 +σ B 2 ) -1 [0.5(p A +p B )-X]<μ A 。
作为变化,假设p A =0和p B =1已知,同时相关性来自投资者认为这两家银行持有相同的投资组合,因此他们知道q 1 =q 2 ,但不知道具体价值。接着,如果他们看到V 1 =0.5,就会推断V 2 =0.5。这些相关性引发了我们所谓的基于推断的传染:在观察到银行1的价值下降后,投资者会根据投资组合的相关性(外部性的来源),从结构和收益的角度推断其他银行的价值。由于投资者对这些投资组合的了解并不充分,他们做出的推断可能事后被证明是正确或错误的。由于银行是复杂金融网络的一部分,而该网络的结构尚不完全清楚,这使得基于推断的传染变得更糟。卡瓦列罗和希姆塞克(Caballero and Simsek,2013)表明,银行间交叉风险暴露网络的复杂性可能导致风险厌恶型银行更多地采取谨慎行动而不是有效率的行动,并且在负面冲击来袭时互相撤回资金。
由于不同类型的外部性和相互连接的交互作用,一家公司可能在网络中很脆弱(例如,从其他失败中推断),并导致连锁反应(例如,不偿还贷款)。因此,对系统性风险的适当评估需要对机构间不同类型的相互依赖性有一个全局观。

即使在基本价值没有任何变化的情况下,系统性风险也会出现。只要金融网络允许多重均衡,仅仅是信念的改变就能使金融体系不连续地从一种均衡转向另一种均衡,并对经济造成真实影响。如前文所述,信念的改变可能源自推断,这些推断反映了真实的潜在相关性;但也可能通过太阳黑子、泡沫或其他视投资者而定的外部事件而改变(Shell,1989;Reinhart and Rogoff,2009)。这里的主要观点是,如果存在多重均衡,那么最终均衡就取决于人们的预期。
传统形式的银行挤兑和恐慌属于由自我实现类行为导致的系统性风险。这种风险来源于银行将短期存款转化为长期非流动性投资的原始角色,这使得银行本质上是脆弱的机构:如果有足够多的储户在银行兑现投资之前取出资金,银行就无法偿还全部存款,从而出现违约。从凯恩斯(1936)到戴蒙德和迪布维格(Dimond and Dybvig,1983)的经典分析都表明,只要预期银行破产,并提取存款,储户就可以诱发银行破产(更多背景资料参见Reinhart and Rogoff,2009)。重要的是,这种风险不一定是由银行的基本面价值下降引发的,而仅仅是由对该机构健康状况的信念转变引发的。甚至有可能是人们知道一家银行是健康的,但是担心其他人对该银行的健康状况不确定。
 这里的无效率来自一种外部性,即储户的投资回报取决于其他储户的行为。投资中的这种互补性导致了多重均衡的存在,因为人们对资产如何估值的预期可能会自我实现,而恐惧会传染。
这里的无效率来自一种外部性,即储户的投资回报取决于其他储户的行为。投资中的这种互补性导致了多重均衡的存在,因为人们对资产如何估值的预期可能会自我实现,而恐惧会传染。
 这甚至适用于一家孤立的银行,进而也适用于金融机构之间没有任何相互依赖的情况。
这甚至适用于一家孤立的银行,进而也适用于金融机构之间没有任何相互依赖的情况。

不仅存款人和外部投资者会感到恐惧并撤出投资,银行也会如此。经济状况的不确定性可能会让银行怀疑许多业务的健康程度。这可以自我实现,因为如果银行担心经济衰退,它们就会撤回资金,要求更高的利率。这可能导致违约,银行可能开始怀疑彼此的健康状况,并停止相互联系,从而使银行更难重新平衡其投资组合。这将导致进一步的信贷紧缩和潜在的螺旋式紧缩,甚至可能导致完全的信贷冻结。同样,这种冻结可以自我实现:
 投资的缺乏恶化了企业和金融中介机构的状况,这使它们成为更糟糕的投资,也证明了撤回投资的合理性(Bebchuk and Goldstein,2011)。因此,即使没有任何基本面变化导致信念发生改变,问题也会产生。这体现在2007—2009年隔夜贷款冻结中(参见Brunnermeier,2009;Diamond and Rajan,2011)。不仅贷款枯竭,而且全球许多股票市场的市值也损失了近一半或更多(例如,道琼斯指数),而潜在的基本面并没有反映出如此剧烈的下跌。央行不得不在银行间贷款市场提供大量流动性。
投资的缺乏恶化了企业和金融中介机构的状况,这使它们成为更糟糕的投资,也证明了撤回投资的合理性(Bebchuk and Goldstein,2011)。因此,即使没有任何基本面变化导致信念发生改变,问题也会产生。这体现在2007—2009年隔夜贷款冻结中(参见Brunnermeier,2009;Diamond and Rajan,2011)。不仅贷款枯竭,而且全球许多股票市场的市值也损失了近一半或更多(例如,道琼斯指数),而潜在的基本面并没有反映出如此剧烈的下跌。央行不得不在银行间贷款市场提供大量流动性。
银行之间的金融合约可能会导致自我实现的违约链。回想一下,银行间合约使银行价值相互依赖。对一家银行无法偿还债务的预期会压低其他银行的价值,并反馈给原银行,使其违约自我实现。在这种情况下,在支付和推断方面都存在外部性。作为一个简化的例子,考虑与第2.2.1节介绍的相同的银行间债权模型和图2所示的网络。为了便于说明,假设两家银行都没有任何外部资产,它们相互之间的欠款为D 12 =D 21 =1,违约银行的资产回收率为零。如果其中一家银行,比如银行1,偿还了另一家银行的债务,那么银行2也有足够的资本全额偿还债务。银行1确实能够偿还欠银行2的债务:这种偿还是自我实现的,并且存在一种均衡,即两家银行都保持偿付能力,并且V 1 =V 2 =0。然而,也存在另一种均衡,即银行违约和V 1 =V 2 =-1。的确,如果银行1预期它不能收回银行2的欠款,它就不能偿还自己的债务,反之亦然。显然,这是一个微型的案例,因为这两家银行可以相互取消对方的债务。然而,在更复杂的循环中,特别是在具有不同形式的合约和不同期限的循环中,这种取消可能难以识别和执行。
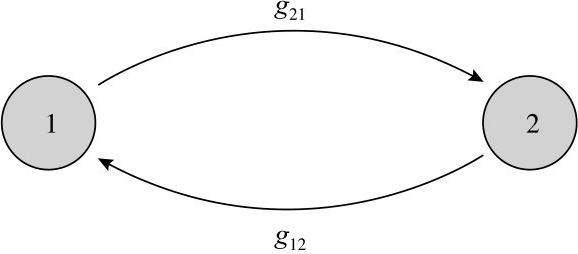
图2 两家银行的环形网络
注:箭头的指向是债权价值流动的方向。
这个例子说明了自我实现的连锁违约与传统的银行挤兑有何不同:它们是由网络中的相互依赖而不是纯粹由信念变化引起的。在任何一个银行间债权有多重均衡价值的风险暴露网络中,都有可能出现自我实现的连锁违约(如El-liott et al.,2014;Roukny et al.,2018;Jackson and Pernoud,2020)。当存在与破产相关的成本时,这种连锁反应非但不能转移违约,还会引发实际的经济成本,而这种均衡的多重性会产生效率后果。
在本节的最后,我们强调,资产持有和抛售的共性也可能产生多重平衡,从而导致金融体系走向自我实现的恶化。例如,假设两家银行持有同一类资产,如果一家银行大量出售该资产,该资产的价值就会下降。这可能是由于缺乏足够的市场深度,也可能是由于人们并不确定银行为何出售资产。在正常情况下,如果两家银行都不被迫出售其持有的资产,资产的价值就会保持在高位,而银行价值高时,两家银行都能保持偿付能力。还有另一种均衡,即两家银行抛售其持有的大量资产,这压低了资产的价格,从而压低了银行的价值。如果一家银行变卖其持有的资产,就会对价格产生足够大的影响,迫使另一家银行也这么做,那么低价抛售的情况就会自我实现。克里希纳穆尔蒂(Krishnamurthy,2010)在投资模型中分析了这种情况,在他的分析中,多重均衡可以共存,并且有不同程度变卖资产和不同价格水平的情况。卡瓦列罗和希姆塞克(2013)考虑了一个模型,该模型结合了由银行之间的交叉风险敞口和低价抛售导致的多米诺骨牌效应。他们表明,有两种可能的均衡:一种是危机蔓延受到控制,价格保持公允;另一种是银行采取谨慎行动,导致低价抛售、低市场价格和更严重的危机蔓延。

在经济困难时期,低价抛售并非加剧银行资产负债表恶化的唯一方式。到目前为止,我们认为银行间的义务(obligations)是固定的,但它们本质上是动态的、不断变化的。如果一家银行预期它将面临低回报,并因此接近违约,那么其他银行在向它提供信贷时会要求更多的抵押品。这使银行的状况进一步恶化,甚至可能加速它的违约,使违约自我实现。

当然,所有这些形式的系统性风险都是相互作用的,而且往往同时在起作用。

我们现在讨论网络结构如何影响系统性风险。由于有关该问题的许多文献都是基于银行之间的债务网络,所以我们大多只关注基于银行间合约的相互依赖关系。
我们首先讨论股票价值下降和债务违约是如何连锁反应的,以及这种连锁反应如何取决于网络的结构和冲击的类型;然后,讨论源于自我实现类反馈(self-fulfilling feedbacks)的系统性风险,并详细阐述产生此类反馈的各种网络模式。
金融网络中的反作用力使得传染在网络密度上具有非单调性。艾略特等人(Elliott et al.,2014)详细研究了这一点,它还适用于各种模型,包括西福恩特斯等人的模型(Cifuentes et al.,2005;Gai and Kapadia,2010;Wagner,2010;Elliott et al.,2014;Gofman,2017;Jackson and Pernoud,2019)。网络密度的非单调性将金融市场中的传染与疾病或思想的传播区分开来,对后者来说,增加互动只会导致更广泛的传播。

随着交易对手的增加,银行变得容易受到价值下降或更多违约来源的影响,这往往会加大发生连锁反应的可能性。然而,在一家银行的总风险敞口不变的情况下,将风险敞口分摊到更多的交易对手身上,可以降低银行对特定交易对手的风险敞口,从而降低危机蔓延的可能性。为了研究这两种力量,艾略特等人(2014)区分了金融机构之间互联互通的两个基本维度:(1)每个机构有多少个合作伙伴,他们称之为网络密度;(2)银行投资组合中与其他机构签订合约的部分,他们称之为网络整合。
我们用一个简单的例子来说明这两种力量的非单调性。考虑一个由相似银行组成的网络,它们的资产负债表如图3a所示。
在负债方面,每家银行有10单位的存款,欠其他银行10单位的债务,银行所有者有2单位的权益。在资产方面,每家银行都有价值12的投资组合和价值10的其他银行的债权。

图3 银行的资产负债表
注:图3a为金融网络中银行的初始资产负债表;图3b为银行投资组合的价值降到10以下,比如8,这将使银行资不抵债,因此银行对某些债务违约。
在这个例子中,我们可以将网络整合度测量为10,即银行的资产中有多少来自其他银行,在该例子中是以银行间债务的形式。这家银行的网络密度为4,即银行的交易对手的数量。因此,这些网络整合度和网络密度导致每个交易对手的风险敞口为2.5单位。在这个例子中,银行还欠四个交易对手每人2.5单位,因此是完全对称的。
现在我们假设其中一家银行的投资组合价值下降,如图3b所示。这家银行现在资不抵债,所以它无法偿付所有债务。就本例而言,由于破产成本,我们将至少一笔贷款的违约视为总违约,尽管显然可以将该示例扩展到处理部分违约。
最初,这家银行欠四家不同的银行各2.5单位,因此它至少有一笔贷款没有偿付。这笔违约贷款必须由向第一家银行提供贷款的对手方冲销,因此第二家银行损失了2.5单位的资产。第二家银行现在也已经资不抵债,并且拖欠了一些付款。再一次,让我们假设存在破产成本,银行无法偿还至少一笔贷款,如图4a所示。这就是违约的连锁反应。

图4 银行的资产负债表
注:图4a,第二家银行由于损失了第一家银行的贷款,现在陷入资不抵债,于是,该银行对某些债务违约。图4b,各家银行都有更多的交易对手,它们之间更低的风险敞口使它们不受单一交易对手违约的影响。
由于银行相互之间的风险敞口为2.5,初始权益价值仅为2,各家银行甚至容易受到单一交易对手违约的影响。在本例中,网络整合度和网络密度都是驱动违约的重要因素。如果银行的网络整合度较低,但密度相同,那么它们对任何给定交易对手的风险敞口都将小于2.5。如果小于2,那么任何单一交易对手违约都不会耗尽一家银行的权益。整合度的提高,也就是说,每家银行对其他银行的风险敞口的增加,往往会加剧传染,就像在这个例子中一样。

类似地,如果银行的网络整合度仍然是10,但密度更大(即更多的合作伙伴),因此,它对任何单一交易对手的风险敞口不超过2,那么连锁反应也将被避免。为了了解密度的重要性,让我们改变例子,使每个银行有10个交易对手,并欠每个对手1单位债务,如图4b所示。因此,整合度相同,但密度增加了。在这种情况下,不再有任何连锁反应。任何单一交易对手的违约不再导致银行破产。
这里我们可以相当清楚地看到非单调性。我们增加了每家银行的交易对手数量,使金融网络更加密集,但我们消除了连锁反应。传染是非单调的,因为如果一开始没有交易对手,就不会有传染。或者,如果我们只有两家银行,彼此配对,那么一家会拖累另一家,但影响不会扩散。有四个交易对手的情况达到了一个平衡点(sweet spot):交易密度高到足以形成一个非常紧密的网络,在这个网络中,事情可以广泛传播,每家银行的风险敞口足以使一笔违约就可能导致交易对手破产。一旦我们增加到10个交易对手,那么一笔违约对任何一个交易对手都不再是大问题。
投资组合中的相关性消除了多样化带来的好处,提高了共同的脆弱性,从而减轻甚至消除了传染中的这种非单调性。为了说明相关性的作用,重新考虑上面的例子(见图4)。假设银行的投资组合表现出显著的相关性,这也许是因为它们都有大量相同的债务抵押债券的敞口,就像2007年的情况一样。例如,假设一家银行的投资组合低于10,其他银行的投资组合也可能低于正常水平。如果我们将图4b中所示的第二家银行的投资组合降到10,同时将第一家银行的投资组合降到8,那么第一家银行的违约就足以将第二家银行推入破产境地,如图5所示。此外,银行资产负债表中的资产进一步降低,这不仅是因为它们的投资组合表现不佳,还因为它们所欠的债务不止一笔同时违约,而这又是因为各银行的价值是相互关联的。


图5 相互关联的投资组合导致传染
注:当存在相互关联的投资组合时,银行更易受其他银行违约的影响,即使它们对任何单一交易对手的风险敞口较小。这可能会抵消文中讨论的多元化和非单调性带来的好处,现在第二家银行即使有10个合作伙伴也可能违约。
理解这种效应的一种方式是,银行间投资的正相关性会抵消交易对手多元化带来的一些好处,并促进传染。更一般地说,增加投资组合的相关性会提高出问题的概率。例如,瓦格纳(Wagner,2010)考虑了两家银行和两种资产,并观察到如果两家银行通过平均配置两种资产来分散其投资组合,那么它们的投资组合是完全相关的。因此,这里存在一个权衡,因为更多元化伴随着银行投资组合之间更强的相关性,会降低每家银行的无条件违约概率,但会提高它们一起违约的概率(假设它们一开始就投资于不同的资产),从而加大系统性风险。当然,最糟糕的情况是银行的投资组合类似,不够多样化,例如,它们都持有类似的抵押贷款或贷款,因为这些投资组合是相互关联的,且风险很大。
正如霍尔丹等人(Haldane,2009;Gai and Kapadia,2010)详细研究的那样,金融网络具有“稳健但脆弱”的属性。
 例如,银行之间以贷款或提供流动性的形式相互依赖,从而允许风险分担,这可以帮助单个机构更少受到单个流动性或投资组合冲击的影响。这些冲击在交易对手之间传播,交易对手的多元化有助于降低单个机构的失败概率。从这个意义上说,金融网络是稳健的。然而,非常大的冲击可能导致某个机构破产,尽管交易对手多元化,但相互依赖可能使冲击的传播更普遍、更广泛。当然,这其中有细微差别,取决于模型和机构之间的合同类型(Allen and Gale,2000;Gale and Kariv,2007;Gai and Kapadia,2010;Battistoni et al.,2012;Elliott et al.,2014;Acemoglu et al.,2015a)。
例如,银行之间以贷款或提供流动性的形式相互依赖,从而允许风险分担,这可以帮助单个机构更少受到单个流动性或投资组合冲击的影响。这些冲击在交易对手之间传播,交易对手的多元化有助于降低单个机构的失败概率。从这个意义上说,金融网络是稳健的。然而,非常大的冲击可能导致某个机构破产,尽管交易对手多元化,但相互依赖可能使冲击的传播更普遍、更广泛。当然,这其中有细微差别,取决于模型和机构之间的合同类型(Allen and Gale,2000;Gale and Kariv,2007;Gai and Kapadia,2010;Battistoni et al.,2012;Elliott et al.,2014;Acemoglu et al.,2015a)。
这与上面讨论的非单调性有关,但又有所不同。稳健但脆弱的特性意味着,在某些情况下,一个网络可能促进了另一个网络,而在另一些情况下,它却可能使情况变得更糟。在上述关于非单调性的讨论中,我们考虑了网络中的变化如何影响某一特定冲击是否产生连锁反应,因此,这是假定冲击不变时对网络的比较静态分析。相反,稳健但脆弱的现象则是要比较某一个特定网络如何应对不同类型的冲击。
阿西莫格鲁等人(Acemoglu et al.,2015a)关注银行间无担保债务网络,并研究银行收益遭受的冲击如何通过网络传播。他们区分了两种冲击:小到足以被金融体系中的总过剩流动性吸收的冲击和不能被吸收的冲击。在前一种类型中,相互依赖明显减轻了危机蔓延的风险:最能抵御危机蔓延的网络结构是全连接网络(complete network),在这个网络中,每家银行的总负债平均分布在所有其他银行。这将导致最大的风险分担和最小的预期违约数量。然而,如果冲击大于金融体系中的总过剩流动性,相互依赖只会促进冲击的传播。我们可以在艾伦和盖尔(2000)的分析中看到这一点。该分析表明,在一个更具体的环境中,冲击蔓延的风险取决于流动性需求是否存在总体不确定性。如果总体不确定性并不存在,那么银行间的联系将使银行可以分担更多风险而不会产生系统性风险。
卡夫拉莱斯等人(Cabrales et al.,2017)强调了冲击规模的作用,在他们的模型中,银行之间的相互依赖就是其投资的相关性。他们考虑的是一组事前相似的银行,每家银行都有外部债务,并能接触到有风险的项目。这些项目的回报受到的冲击在各个银行间是独立同分布的。如果一家银行无法偿还外部债务,它就会违约,并因陷入困境而产生一些成本。银行可以通过交换对彼此项目的债权来实现投资组合的多样化:从i到j的连接表示i银行对j项目的收益索取权。因此,在卡夫拉莱斯等人的模型中,银行和项目之间的连接表示银行间投资组合的相关性,而不是银行间债务。于是,同样的权衡就出现了:更多的连接可以更好地分担风险,但也意味着暴露在更多的风险中。何种网络结构的预期违约次数最少,由冲击的分布决定。特别是,卡夫拉莱斯等人(2017)表明,如果存在较大的冲击,则空网络(empty network)是最优的。如果冲击大多较小,那么完全对称网络是最有韧性的。其他的冲击分布可以产生使传染最小化的中等网络密度。
阿西莫格鲁等人(2015a)描述了在不同冲击类型下对传染最有韧性或最没有韧性的网络结构。如果冲击很小,整个网络的传染风险最低。相比之下,环形网络是最容易传染的网络结构,在环形网络中,每家银行的债权都集中在一个交易对手身上。该分析适用于常规网络,即所有银行的银行间债权与负债数量相同,交易对手数量相同。这排除了银行规模和关联度的异质性,以及银行成为净贷款人或净借款人的可能性。
为便于分析,一种处理方法是限于对简单情形的归纳总结。另一种方法是利用大型随机网络的特性。这两种方法都可以提供有价值的见解且具有可操作性,但只适用于有限类别的网络。
一个挑战是,金融网络经常涉及重大的不对称性,比如存在核心-外围结构,这影响了传染的风险。大型核心银行可以抵御小冲击,但当遭遇大冲击时,尤其是当这些冲击相互关联时,它们可能会遭遇灭顶之灾。这一点很重要,如艾略特等人(2014)通过模拟研究,证明了核心-外围网络也可以消除第3.1节中讨论的非单调性的某些方面,其原因在于,如果核心银行对某一个大型银行或实体有大量风险敞口,那么这家银行或实体的倒闭可能导致核心银行内部的广泛传染,然后蔓延到整个系统。这就是2008年出现的情况。也有其他研究提供了证据,证明异质性至关重要。例如,有模拟研究(Gai et al.,2011)表明,传染随银行间债权网络的集中度而变化。还有研究(Glasserman and Young,2015)提供了一些理论结果,表明在某一类网络中,当银行的规模不同且冲击源自大型银行时,传染是最大的。另有研究(Teteryatnikova,2014)说明了相邻银行连接度(即交易对手的数量)之间的负相关有助于提高网络的韧性。
鉴于分析的复杂性,我们有必要从两个方向继续我们的分析:一个方向是深入了解网络结构的异质性如何影响金融传染,以及通过具体的应用,为了解普遍存在的重要网络特征提供经验研究方面的背景。另一个方向是将传染模型应用于观察到的网络,以模拟风险模式,监管机构越来越倚重这种方法(Aikman et al.,2009;Basel Committee on Banking Supervsion,2015)。
接下来,我们将讨论网络结构如何影响第二类系统性风险:导致多重均衡的自我实现的反馈效应。
目前正在兴起的一类文献强调了循环在生成多重均衡中的作用(Roukny et al.,2018;D'Errico and Roukny,2019;Jackson and Pernoud,2020),如图2所示。在银行间债务网络中,循环会增加交易对手风险,却不会在金融体系中创造价值;因此,清算循环在不影响银行价值的情况下降低了连锁违约的风险。例如,有研究(Roukny et al.,2018)表明,当且仅当存在一个由充分互联的银行组成的循环,即一家银行的偿付能力依赖于循环中前一家银行的偿付能力时,银行价值才存在多重均衡。
作为一个例子,请考虑图6所示的金融网络。在图6a的金融网络中,如果没有银行偿付其债务,那么假定每家银行的投资组合价值为10,小于银行所欠的债务,则没有一家银行能清偿债务。所有银行都资不抵债,没有债务得到清偿就成为一个自我实现的均衡。另一个均衡是所有债务都得到偿还。相比之下,在图6b的金融网络中,总债务被勾销,只剩下净债务。此外,还有一个独特的均衡,在这个均衡中,所有银行都有偿付能力。清除所有的循环消除了多重均衡的可能性,并确保只有最好的均衡。因此,清算循环可以带来巨大收益,特别是当人们预期银行和更广泛的投资者持有悲观信念或者相信他人持有悲观信念时。
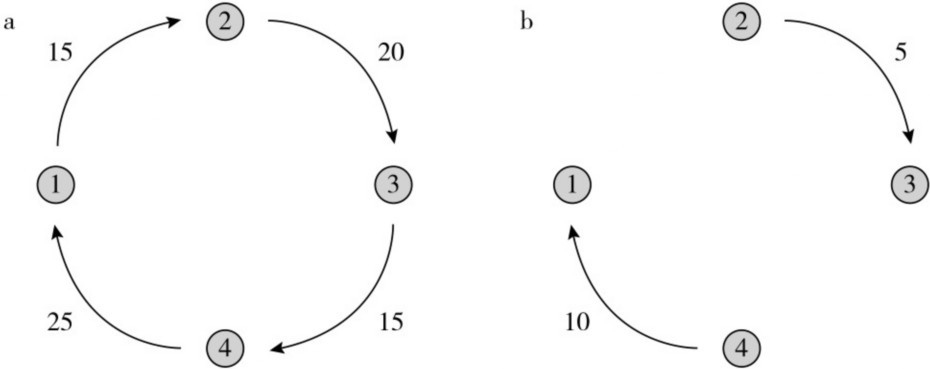
图6 循环的作用
注:图a和图b中的两个网络有相同的净债务,但图a有循环,图b没有。所有银行都有价值为10的投资组合。如果一家银行破产,它就无力偿还债务。在图b的网络中,存在一个唯一的均衡,即所有银行都有偿付能力。在图a的网络中有两种均衡:一种是所有银行都无力偿债并违约,另一种是没有银行违约。
当然,这是一个典型例子,以表明银行如何消除其债务,并避免坏的均衡。然而,在实践中,这些循环要复杂得多,涉及许多银行、不同的债务期限或合约类型,以及可能导致惯性和协调失灵的其他因素,特别是在时间不确定和人们延迟偿还债务的情况下。因此,重要的是要了解什么时候循环会出现问题,以及当循环存在时如何克服它们。
杰克逊和佩尔努(2020)详细研究了自我实现的连锁效应和信贷冻结,并描述了它们如何依赖于循环的存在、银行的投资组合,以及与破产相关的成本和延迟。
 如果一些银行的总风险敞口较小,这种自我实现的连锁反应和信贷冻结就不太可能发生,因为这些银行可能有足够的资本作为缓冲,阻止连锁反应。如果某个循环中没有一家银行有足够的外部资产来触发该周期内的连锁偿还,就会出现自我实现的反馈效应。杰克逊和佩尔努(2020)也考虑了银行之间更一般的金融合约,并描述了多重均衡的存在,表明它们是由一种特定类型的循环产生的,其中涉及一些债务,但也可能涉及其他合约。但是,他们表明,不涉及某些关键债务义务的周期性结构不可能导致多重平衡。这种对网络周期性结构的描述不仅解释了多重均衡和信贷冻结,而且为确定使金融网络恢复偿付能力所需的最低救助提供了基础,如下文所述。
如果一些银行的总风险敞口较小,这种自我实现的连锁反应和信贷冻结就不太可能发生,因为这些银行可能有足够的资本作为缓冲,阻止连锁反应。如果某个循环中没有一家银行有足够的外部资产来触发该周期内的连锁偿还,就会出现自我实现的反馈效应。杰克逊和佩尔努(2020)也考虑了银行之间更一般的金融合约,并描述了多重均衡的存在,表明它们是由一种特定类型的循环产生的,其中涉及一些债务,但也可能涉及其他合约。但是,他们表明,不涉及某些关键债务义务的周期性结构不可能导致多重平衡。这种对网络周期性结构的描述不仅解释了多重均衡和信贷冻结,而且为确定使金融网络恢复偿付能力所需的最低救助提供了基础,如下文所述。
清算循环带来的收益可以解释投资组合压缩(portfolio compression)这种风险管理技术的使用(D'Errico and Roukny,2019)。该技术包括旨在减小银行间总风险敞口以降低监管要求的净额结算机制。类似的观点也经常用于讨论通过中央结算对手方(CCPs)结算双边场外交易(OTC)的好处。集中交易平台允许银行间合约的多边净额结算,这提高了金融网络的透明度,并限制了交易对手风险。
 如果银行间合约仅限于债务合约,这种多边净额结算属于结算循环,如图6所示。
如果银行间合约仅限于债务合约,这种多边净额结算属于结算循环,如图6所示。
系统性风险取决于若干内生因素,包括网络结构、金融机构的投资组合及其相关性,这些因素是网络中各个金融机构决策的结果。因此,至关重要的一点是,了解金融机构是否有有效的激励机制,也就是说,金融机构有激励做出使金融体系整体价值最大化的投资和选择伙伴策略。
鉴于金融网络充满了外部性,我们可以预测,个体的财务激励可能与整体经济福利并不一致。文献表明,激励机制在许多方面都是错位的。我们首先论述银行之间的相互联系以及由此导致的传染可能性如何影响银行在外部资产上的投资决策。然后,我们研究银行选择其银行间资产(interbank assets)的激励机制,以及这些激励机制如何影响均衡网络结构。
相关文献强调了银行投资决策中的两大扭曲:一是它们有承担过多风险的激励,二是将自己的投资组合与交易对手的投资组合过度关联。我们将讨论网络结构如何在这两种无效率的情况下发挥作用。
金融相互依赖主要通过两种方式导致银行承担了相对于社会最优情形而言过多的风险,这两种方式都与第2节中提到的两种系统性风险有关。
首先,银行的投资决策不仅影响银行自身的价值,还间接影响其交易对手的价值,以及交易对手的交易对手的价值,以此类推。这种外部性在金融网络中并不新鲜:很多时候,投资选择可能并不反映所有受影响者的利益(Admati and Hellwig,2013),詹森和梅克林(Jensen and Mecling,1976)对此早有分析,在他们的分析中,经理人的选择并不反映股东的利益。学者们研究了各种网络中的利益不一致(Brusco and Castiglionesi,2007;Hirshleifer and Teoh,2009;Galeotti and Ghiglino,2021;Jackson and Pernoude,2019;Shu,2019),在这些网络中,外部性广泛存在,利益远远超出与一家机构直接相关的范围。
例如,杰克逊和佩尔努(2019)探讨了以下的投资组合选择问题,其中每家银行i都投资于安全资产和风险资产,安全资产有固定收益率1+r,风险资产有随机收益率
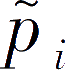 ,且E(p
i
)>1+r。此外,银行之间还通过金融合约相互关联,这些金融合约要么采取债务的形式,要么采取股权的形式。只要银行与网络中的某一类循环无关,完全投资于风险资产就是银行的严格占优策略,即使这可能导致过度的系统性风险。直观地说,只有特定的循环会导致银行的风险行为可能触发连锁违约,而后通过网络反馈给自身。如果没有这种反馈风险,银行在权衡高风险投资的收益和成本时,就会忽略它们触发的任何外部成本,这可能会导致它们过度投资于风险资产。
,且E(p
i
)>1+r。此外,银行之间还通过金融合约相互关联,这些金融合约要么采取债务的形式,要么采取股权的形式。只要银行与网络中的某一类循环无关,完全投资于风险资产就是银行的严格占优策略,即使这可能导致过度的系统性风险。直观地说,只有特定的循环会导致银行的风险行为可能触发连锁违约,而后通过网络反馈给自身。如果没有这种反馈风险,银行在权衡高风险投资的收益和成本时,就会忽略它们触发的任何外部成本,这可能会导致它们过度投资于风险资产。
其次,网络的相互依赖使银行的各种决策形成策略性互补,导致社会无效率的结果。例如,有两位学者(Allouch and Jalloul,2018)考虑了一个银行间负债网络,在这个网络中,银行有可能存储部分初始现金流,以克服未来的净赤字,而不是以放弃未来回报为代价立即兑现这些收益。他们表明,这可以被视为一个协调博弈,银行在其中选择违约或不违约。银行的决策是策略性互补的,因为如果其他银行也有偿付能力,那么一家银行就更容易保持偿付能力。他们表明,如果网络中存在债务循环,就会存在坏的均衡,即银行选择提前套现,然后违约,因为它们预期其他银行也会这样做。这些均衡是无效率的,因为如果所有银行及其外部债权人都能在保持偿债能力方面进行协调,它们的境况都会更好。
有许多力量推动金融机构将其投资相互关联。有些是基本的羊群力量:从别人做出的投资中可能看到了有关投资前景的某些信息(Banerjee,1992;Bikhchandani et al.,1992;Chincarini,2012),或者选择投资的人可能会担心自己的声誉(Scharfstein and Stein,1990)。推动投资相关联的另一些因素是限制投资范围的监管规定,这本质上是在推动银行持有某些类别的资产或某些资产的最低数量,或拥有符合某些风险特征的投资组合。还有一些力量迫使银行采取与其竞争对手相同的贷款策略(Cohen-Cole et al.,2015)。尽管此类监管的目的是让投资组合更安全,但它们迫使银行持有类似资产的事实可能会让许多机构同时遭受罕见的负面冲击(例如,重大主权债务违约)。
除了这些力量,还有网络力量。第一个重要方面是监管机构在决定是否救助破产银行时的激励。如果更多的银行同时倒闭,就更有可能触发一连串违约,监管机构也有更多的动机介入。阿查里亚等人(Acharya and Yorulmazer,2007)强调了这个“多到不能倒”的问题,这个问题激励银行将其投资组合关联起来,因为如果它们一起破产,就更有可能得到救助。银行从众的另一个驱动力是信息传染的风险,如我们在第2节所述。在一个不完全信息的世界里,一些银行的不良信息可能会增加其他银行的借贷成本,因为投资者会下调后者的信誉。这样的推断也会使不相关联的投资组合的价值降低,正如阿查里亚等人(2008)表明的,银行更喜欢相互关联的投资。艾略特等人(2018)详细介绍了另一种力量,他们考虑了一个模型,在该模型中,银行可以互换对彼此投资的索取权,以对冲风险敞口的冲击。银行间没有债务,但每家银行都欠外部投资者一些债务。因为股东是根据有限责任采取行动的,他们有动力将损失从他们身上转移到债权人身上。这种风险转移促使银行将它们的投资组合收益关联起来,这样一来,如果一家银行受到巨大冲击,其他银行也会受到冲击,它们都会违约,损失则由债权人承担。最后,杰克逊和佩尔努(2019)提出了一个兼顾银行间债务和股权的模型,表明激励机制如何依赖于交易对手的投资组合。在其他条件相同的情况下,如果一家银行最多的收益来自它与其他银行签订的合约,它就更愿意拥有偿付能力。这使它在其他银行有偿付能力时更愿意有偿付能力,而在其他银行破产时更愿意无偿付能力,从而使交易对手之间的投资组合完全相互关联成为一种均衡。事实上,从银行股东的角度看,它是帕累托占优均衡。
私人部门的监督和声誉也有助于缓解激励问题,因为这会使糟糕的投资增加金融机构的资本成本(Godlewski et al.,2012;Godlewski and Sanditov,2018)。这可能会影响银行对投资组合和网络合作伙伴的选择。尽管监督和声誉机制可以缓解一些问题,但道德风险问题通常不会因此消失(Diamond,1991;Rajan,1992;Holmstrom and Tirole,1997)。在金融网络中,这些反馈如何影响银行的激励是一个有待讨论的重要议题。
我们现在论述银行在金融网络中选择交易对手时的激励,并强调无效率。从杰克逊和沃林斯基(Jackson and Wolinsky,1996)的工作开始,无效率的网络形成是文献中反复出现的一个主题,但它在金融机构的背景下以特殊的方式表现出来。
有几个因素可以导致核心-外围结构(在许多金融市场中观察到)内生地出现,其中一些因素是基于核心银行作为金融市场中介发挥的各种作用。有研究(Babus and Hu,2017)表明,当银行之间的合作关系不仅具有交易功能而且具有信息功能时,金融市场中介就存在规模经济,均衡网络具有星型结构。中央代理人拥有所有其他代理人的信息,执行所有合约,并成为所有交易的中介(收取一定的费用)。由于星型网络将所有相关信息集中在一起,因此效率有限。法布迪(Farboodi,2017)研究了推动中介的不是信息摩擦,而是银行在获得投资机会上不平等的情形。能够利用这个投资机会的银行成为核心银行,资金从外围银行流入这些银行。这种均衡网络是社会无效率的,表现为核心银行互联互通,而外围银行缺乏互联互通,核心银行由此攫取了中介租金。最后,正如有研究(Wang,2017)指出的,核心-外围结构也可能源于库存的规模经济。在一个机构有随机交易需求的市场中,中介机构的出现是为了促成这些交易。这就导致了中介机构的随机库存,集中化的中介机构通过大数定律降低了库存风险。这中和了中介机构的市场势力。正如该研究所示,这将导致一个社会无效率的均衡网络,由资产交易频率决定的交易商(核心银行)要么太少,要么太多。
除了核心-外围结构之外,银行选择的交易对手数量本身也会导致无效率,因为它会影响系统性风险,而系统性风险不会被银行完全内部化。阿西莫格鲁等人(2015b)的研究表明,银行相互之间往往发放过多的贷款,而且这些贷款在借款银行之间不够分散。尽管均衡利率反映了借款人的冒险行为,但银行间负债的这种不够分散仍然存在:双边外部性通过均衡利率被内部化,而更普遍的网络外部性则没有被内部化,导致均衡网络的社会无效率。同样,杰克逊和佩尔努(2019)的分析表明,银行倾向于选择持有较少交易对手的债权,因为它们忽视了其他人在破产时产生的传染成本。

此外,均衡网络在外部资产的投资组合上表现出同质性(Elliott et al.,2018):银行更愿意成为拥有类似投资组合的其他银行的交易对手。这是选择与交易对手相似的投资组合的另一种原因。在选择持有谁的债权时,承担有限责任的银行低估了多元化的价值,更愿意与拥有类似投资组合的银行联系在一起。这意味着,当冲击袭来时,银行会一起违约,并将损失转嫁给债权人。
无效率并不是讨论金融网络形成的相关文献得出的唯一预测。一些论文论述了那些推动形成避免广泛传染的网络的力量。尤其是,巴布斯(Babus,2016)表明,如果银行能够承诺相互确保彼此免受流动性冲击,就可以形成传染永远不会发生的均衡。埃罗尔和沃拉(Erol and Vohra,2018)考虑了多家可以切断外部连接并重组其连接的银行出现偏差时仍保持稳定的网络。在他们的模型中,一旦有一个交易对手违约,银行就会违约;因此,如果某一网络组成部分中的任何一家银行违约,所有银行都会违约。考虑到建立联系带来的积极好处,每家银行应该与它有途径联系的所有银行建立联系。由此我们可以预测,一个稳定的网络将是一组完全连接的不相交集群的集合。群体稳定性确保每个集群中的银行数量将使其整体价值最大化。尽管经验观察到的网络具有更多的异质性,但埃罗尔和沃拉(2018)的结论背后的推理可以帮助解释为什么核心-外围网络中的核心通常是完全连接的。
最后,对危机蔓延的担忧可能导致信贷冻结,银行因此不再相互放贷,导致网络过于稀疏。阿西莫格鲁等人(2020)讨论了信贷冻结的程度如何取决于银行潜在合作伙伴关系的潜在网络结构和流动性冲击的分布。他们表明,由于中介摩擦(intermediation frictions),金融体系可能无法有效地将资金从储户配置到企业家手中。
现在,我们转而讨论关心整体社会福利并理解上述系统性风险和无效率的政府当局实施监管的相关问题。
至此,我们已经清楚地认识到,要想恰当地应对系统性风险,就需要对金融网络有全面的认识。
 为了评估哪些机构是需要监管和/或救助的关键机构,了解网络细节至关重要,对此我们将给出解释。
为了评估哪些机构是需要监管和/或救助的关键机构,了解网络细节至关重要,对此我们将给出解释。
系统性风险评估的一个重要组成部分是压力测试,它通常以分散的方式运行。许多压力测试的主要输入是资产负债表数据,这些数据描述了每家银行持有的金融资产和负债的情况。在不同的司法辖区,资产负债表数据并不总能提供有关交易对手的完整甚至部分信息,因此也不提供有关网络结构的信息。这样的本地数据可能完全遗漏了哪些银行最有可能开始违约或陷入违约的信息。这一点不言自明,但考虑到它的重要性,值得强调。
为了便于说明,考虑这样一个网络,其中银行仅通过债务合约联系在一起。基于本地资产负债表信息的系统性风险衡量标准只取决于每家银行资产和负债的账面价值,而不取决于其交易对手的身份。为了说明为什么这是不充分的信息,我们给出了一个金融网络的例子,其中两家银行有相同的资产负债表,但它们的违约有显著不同的后果。因此,如果政府只能够救助两家机构中的一家,它就无法根据当地信息做出最优决策。
特别是,请考虑图7所示的网络。假设银行1和银行4的投资组合收益率都为0,因此它们都无力偿债。设银行2从其投资组合中获得的收益介于3D/4和D之间,银行3获得低于D/4的收益,银行5获得高于D/2的收益。假设违约银行的资产回收率为零。尽管银行1和银行4拥有相同的资产负债表,但只有银行1继续资不抵债的情况下,才会引发广泛的违约蔓延。事实上,银行2和银行3有足够的缓冲来吸收银行4违约带来的冲击,但不足以吸收银行1违约带来的冲击。因此,救助银行1可以防止整个金融体系崩溃,而救助银行4并不能改变任何事情,整个金融体系的崩溃仍会发生。
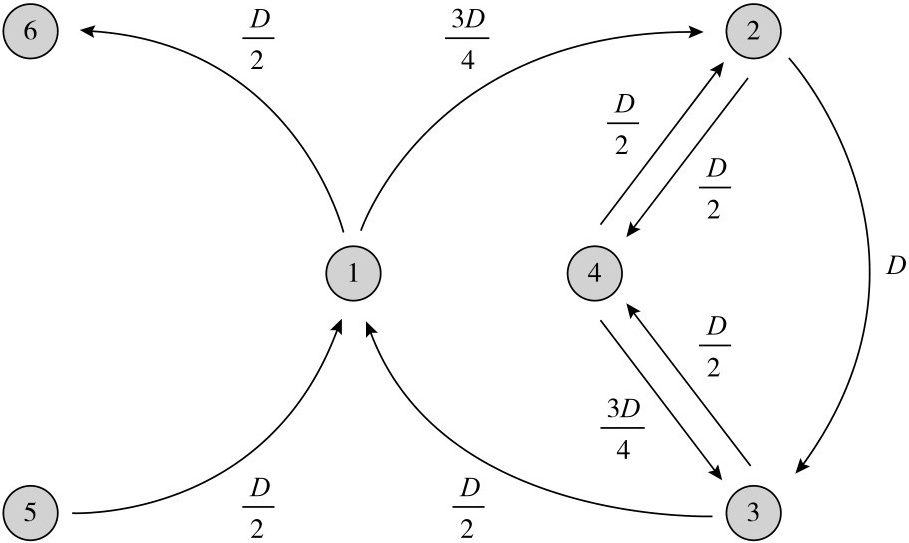
图7 银行网络和对银行的救助
注:箭头所指的方向表示欠债。银行1和银行4有相同的资产负债表:它们都对其他银行有两笔债权(都是D/2)和两笔债务(一笔为D/2,另一笔为3D/4)。它们都是净负债方。
这个例子也充分说明了一个事实:如果没有关于网络的信息,人们甚至无法确定哪些银行面临资不抵债的风险。例如,如果查看银行3的资产负债表,但不知道银行2对银行1的风险敞口,那么即使知道银行3的交易对手的投资组合变现情况,但不知道银行1濒临破产,也会以为银行3没有资不抵债的危险。虽然这是一个简单的例子,但它说明了为什么不了解金融网络的各个部分(如外国机构、影子银行等),或者只有来自本地压力测试数据的监管机构处于不利地位。
因此,一定程度上受2008年金融危机的教训推动,涉及金融网络中重要部分的系统性风险评估开始出现。例如,欧洲央行拥有其辖区内大多数银行最大风险敞口涉及的交易对手的信息。这使得构建一个由欧洲银行业的部分资产和负债以及一些欧洲以外银行的动向指标组成的网络成为可能。因此,对网络中某个重要部分的系统性风险的一些计算开始出现(参见Covi et al.,2019;Farmer et al.,2020)。同样,英格兰银行有英国各银行之间双边交易的监管数据,使得它可以对不同资产类别的英国银行间网络进行分析(Ferrara et al.,2017;Bardoscia et al.,2018)。这是评估系统性风险的一个重要进展,但我们还需要做更多工作,尤其是在欧洲以外的地区,以及日益壮大的影子银行体系。影子银行体系不受大多数司法辖区的管辖。
掌握有关网络的一些信息,并理解上文讨论的问题,我们就可以考虑金融市场的最佳干预措施。我们将分两部分讨论这个问题:一部分是避免连锁效应,另一部分是在多个潜在结果的情形下避免坏均衡和负反馈循环。让我们从第二部分开始。
文献已经提出了监管机构可以干预的几种方式,以应对源自多重均衡和自我实现类危机的系统性风险。这类危机是金融市场中部分机构出现协调问题导致的结果。例如,当存款人协调失灵,所有人都取出存款时,就会出现银行挤兑;当所有银行都选择不放贷时,就会出现信贷冻结。重要的是,在这两种情况下,都存在另一种均衡,即不发生危机,这是所有人都希望看到的。消除这种系统性脆弱来源的一种方法是让监管机构为所有贷款提供保险,要么通过存款保险(Diamond and Dybvig,1983),要么承诺成为最后贷款人,在必要时注入资金(Bebchuk and Goldstein,2011;Diamond and Rajan,2011)。如果这些措施可信,就可能消除协调失灵。
由协调失灵导致的自我实现的危机,不同于因基本面损失引发的传染危机,因为自我实现类危机可以在不需要监管机构付出任何资本成本的情况下结束。这是两种系统性风险之间的一个关键区别。通过为存款或贷款提供担保,监管机构可以确保不会有银行挤兑或信贷冻结导致银行违约,因此监管机构不必干预均衡。
即使监管机构事先没有为银行拆借提供保险,并且出现了自我实现的连锁违约或信贷冻结(图2),通过适当地向网络注入(至少部分可收回)资金,这种连锁反应或信贷冻结仍然可以结束。杰克逊和佩尔努(2020)表明,这种连锁反应源于网络中存在的索债循环,因此,要阻止连锁反应,就需要注入足够多的资本来清除索债循环。注资是启动偿债循环的一种方式,可以避免坏的均衡。杰克逊和佩尔努还表明,监管机构可以收回向自我实现的索债循环注入的全部资金,从而使这部分救助政策几乎不需要付出成本。为了说明这一点,请重新考虑图6a所示的网络。例如,如果有人向银行1或银行3注入5单位资本,就会出现唯一均衡,在这个均衡中,所有银行都有偿付能力:银行1可以向银行2支付资金(即使没有来自银行4的任何资金流入),然后银行2可以向银行3支付资金,以此类推。此外,一旦所有债务都还清,注资当局就可以收回这些资金。相反,请注意,向银行2或银行4注入5单位资金却不会有同样的效果:“所有银行都违约”的坏均衡仍将存在。更一般地说,正如杰克逊和佩尔努(2020)表明的,为了确保只保留最优均衡,应当把资金注入某些最具优势的关键银行,这取决于银行的支付可为网络提供的杠杆大小,也取决于哪些银行同时参与多个循环,后一种情况会在更复杂的网络中出现。杰克逊和佩尔努(2020)描述了恢复偿付能力所需的最小资本注入,并表明,当涉及多个银行时,找到最小注资的方法是一个复杂的NP难题。然而,他们也表明在一些结构良好的网络中,如核心-外围网络,由于核心银行的规模和资产负债表存在一定的对称性,因此找到最优救助政策更简单易行。
避免协调失灵和自我实现类危机的另一种方案是让所有交易都通过中央对手方。集中化是有帮助的,因为它允许债务的多边净额结算,这消除了索债循环,并减少了多重均衡的可能性。有研究(Csóka and Herings,2018)强调了银行间支付清算集中化的好处。他们表明,集中化的清算过程总能产生银行价值的最优均衡,而分散化的清算过程则收敛到最差的均衡。
当然,这些干预措施可能会事前扭曲银行的投资激励,导致它们承担更多风险,从这个意义上说,可能会付出社会代价。我们将在第5.3节讨论监管和激励之间的相互作用。
正如第2.2节所述,一些金融机构的最初损失可能会由于网络的相互依赖而被放大,并在整个金融系统中蔓延。随之而来的破产成本是经济遭受的实际损失,但通过干预可以避免这一损失,或者至少将这一损失降至最低。
监管机构有两种主要的干预方式。第一种是对银行的事前监管,以确保能避免无效率的高风险投资。这可以通过各种形式的审慎监管来实现,例如,规定准备金、流动性或资本要求;
 限制不同机构可以进行的投资类型;并随时监督银行的资本充足率和投资。第二种方法是允许任意投资,但如果出现连锁违约的风险,则进行干预并注入资金,将传染降至最低。正如杰克逊和佩尔努(2019)所示,人们是否想要干预取决于相关银行的金融中心度(详见下文)。
限制不同机构可以进行的投资类型;并随时监督银行的资本充足率和投资。第二种方法是允许任意投资,但如果出现连锁违约的风险,则进行干预并注入资金,将传染降至最低。正如杰克逊和佩尔努(2019)所示,人们是否想要干预取决于相关银行的金融中心度(详见下文)。
 如果一家银行的中心度足以带来巨大的系统性风险,那么事前监管更好还是事后救助更好,取决于相对于救助的实际成本,监管的机会成本,即迫使银行持有更安全资产而损失的超额收益有多大。
如果一家银行的中心度足以带来巨大的系统性风险,那么事前监管更好还是事后救助更好,取决于相对于救助的实际成本,监管的机会成本,即迫使银行持有更安全资产而损失的超额收益有多大。


我们可以利用金融中心度的概念来确定哪些金融机构对系统性风险的贡献最大。文献提出了几种中心度的衡量方法,其目的是评估某一银行的系统性风险敞口或银行自身对系统性风险的贡献。
 其中一些衡量方法仅基于单家银行的投资组合回报的市场数据,包含了通过低价抛售(Duarte and Eisenbach,2018;Engle and Ruan,2019)或银行投资组合回报的相关性结构(Billioet al.,2012)而形成的传染性特征。另一些衡量方法则基于银行间合约的基础网络,并利用通过交易对手风险而传染的模型(Amini et al.,2016;Hauton and Héam,2016;Jackson and Pernoud,2019)。例如,杰克逊和佩尔努(2019)提出了一种方法,用于衡量银行的金融中心度,该方法基于基本资产价格从p变化到p′时的系统性影响。考虑一个银行间合约和债务网络,我们可以追溯这种变化将如何通过网络蔓延,并影响所有机构的偿付能力和价值。通过观察某家银行的投资组合变化如何产生连锁反应,可以评估该银行的系统重要性,以此评估金融体系中所有外部投资者的价值最终发生的总变化。
其中一些衡量方法仅基于单家银行的投资组合回报的市场数据,包含了通过低价抛售(Duarte and Eisenbach,2018;Engle and Ruan,2019)或银行投资组合回报的相关性结构(Billioet al.,2012)而形成的传染性特征。另一些衡量方法则基于银行间合约的基础网络,并利用通过交易对手风险而传染的模型(Amini et al.,2016;Hauton and Héam,2016;Jackson and Pernoud,2019)。例如,杰克逊和佩尔努(2019)提出了一种方法,用于衡量银行的金融中心度,该方法基于基本资产价格从p变化到p′时的系统性影响。考虑一个银行间合约和债务网络,我们可以追溯这种变化将如何通过网络蔓延,并影响所有机构的偿付能力和价值。通过观察某家银行的投资组合变化如何产生连锁反应,可以评估该银行的系统重要性,以此评估金融体系中所有外部投资者的价值最终发生的总变化。
从另一个角度看,德芒热(Demange,2016)提出了一个衡量银行间负债网络溢出效应的方法,该网络依赖于银行间均衡债务支付的属性。她将一家机构的威胁指数定义为其直接持有的资产增加对系统中总债务偿还的边际影响。该指数对所有具备偿付能力的机构无效,因为它们有能力全额偿还债务。对违约机构来说,这一指数严格为正,因为更大的投资组合意味着它们可以偿还更大比例的债务,这可能会使其他银行偿还更多的债务,以此类推。然后,该机构的威胁指数可以反映这种威胁在网络中传播的程度。这可以看作上述方法的边际版本,边际指的是足够小的变化,不改变违约情况,而是改变偿付流。
对监管机构来说,公共救助是有成本的,尤其是当政府债券由债务融资时,它们会压低政府债券的价格。如果银行持有大量主权债务,这将进一步恶化它们的投资组合价值,而且需要更大规模的救助来维持其偿付能力。这种“厄运循环”是大衰退之后欧洲主权债务危机的一个关键因素。卡波尼等人(Capponi et al.,2020)提出了一个包含这种放大机制的模型,并描述了这种情况下的最优救助。
所有这些论文都关注金融组织的网络,但监管机构应该关注金融网络对整体经济的影响。传染的确不是金融市场特有的,例如,投入产出网络的结构和供应链可以放大小冲击,就像金融网络可以放大对收益的冲击并影响资产价格(Acemoglu,2012;Barrot and Sauvagnat,2016;Ramírez,2017;Herskovic,2018)。因此,在决定最优资本注入时,需要很好地理解金融网络和供应链之间的相互作用,这是一个尚未受到很多关注的话题。
上一节考虑了应对系统性风险的干预措施,但考虑了网络和投资组合。当然,这些都是内生的,监管的变化可能会影响它们。对监管与市场参与者激励之间的相互作用,人们了解有限。考虑市场参与者对监管的反应,可能会改变比较静态的一些结论和政策含义。
旨在降低系统性风险的监管可能会对银行的投资激励产生负面影响。例如,如果预期得到救助,可能会导致道德风险,因为银行不再承受风险投资的成本。
 其作用机制是微妙的,因为在救助期间,控制银行的股东可能不会获利,而债务人会。然而,银行管理层可能有多种理由希望避免与股权价值无关的资不抵债。有证据表明这很重要;例如,有研究(Dam and Koetter,2012)发现,救助导致德国银行承担了更多的风险。同样,凯罗米里斯和亚雷姆斯基(Calomiris and Jaremski,2019)研究了19世纪早期美国引入存款保险的影响。他们发现,存款保险削弱了市场纪律,导致银行承担更多风险。因此,降低流动性风险是以更高的资不抵债风险为代价的,因为这扭曲了银行的激励。公共救助不仅影响银行的投资决策,也影响它们对交易对手的选择,从而影响金融网络的均衡结构(Erol,2019)。在没有救助的情况下,为了应对交易对手(更重要的是二级交易对手)的可能风险,一个高聚类、低集中度的网络就会内生地出现。然而,对救助的预期使得银行对传染风险的担忧降低,从而引入了一种网络道德风险(network hazard),使得均衡网络具有低聚类、高集中度的特点。这种救助的反常效应,加剧了它们引发的更常见的道德风险问题。
其作用机制是微妙的,因为在救助期间,控制银行的股东可能不会获利,而债务人会。然而,银行管理层可能有多种理由希望避免与股权价值无关的资不抵债。有证据表明这很重要;例如,有研究(Dam and Koetter,2012)发现,救助导致德国银行承担了更多的风险。同样,凯罗米里斯和亚雷姆斯基(Calomiris and Jaremski,2019)研究了19世纪早期美国引入存款保险的影响。他们发现,存款保险削弱了市场纪律,导致银行承担更多风险。因此,降低流动性风险是以更高的资不抵债风险为代价的,因为这扭曲了银行的激励。公共救助不仅影响银行的投资决策,也影响它们对交易对手的选择,从而影响金融网络的均衡结构(Erol,2019)。在没有救助的情况下,为了应对交易对手(更重要的是二级交易对手)的可能风险,一个高聚类、低集中度的网络就会内生地出现。然而,对救助的预期使得银行对传染风险的担忧降低,从而引入了一种网络道德风险(network hazard),使得均衡网络具有低聚类、高集中度的特点。这种救助的反常效应,加剧了它们引发的更常见的道德风险问题。
目前,关于金融网络结构如何响应监管变化的实证研究很少。一个值得注意的例外是安德森等人最近的一项研究(Anderson et al.,2019),该研究考察了1863—1864年《国家银行法案》对美国银行体系拓扑结构的影响。《国家银行法案》确立了准备金和资本要求,并建立了准备金等级制度。这使得银行系统更加集中于几家位于指定储备城市的核心银行。这有利于更好的分散化,但如果其中一家核心银行倒闭,危机蔓延的可能性也会加大。
鉴于公共救助的高额经济成本及其产生的负面激励,私人部门对违约的解决方式引起了人们的关注,特别是自2008年金融危机以来。私人部门可能有激励自救,也就是说私人银行在资不抵债时互相救助,而这种激励取决于金融网络的拓扑结构。如果阻止另一家银行违约的收益高于救助成本,那么救助另一家银行就符合银行的利益。自救的收益来自银行间资产的价值,如果避免违约,银行间资产的价值就会提高。这意味着,银行之间的连接不仅会传播冲击,而且会激励私人部门自救,这样一个联系更紧密的金融体系可以降低系统性风险,并导致更多的投资(Leitner,2005)。卡尼克(Kanik,2019)说明了破产成本如何促使私人部门自救,因为它们会放大违约造成的损失。
 卡尼克研究了银行联合行动以避免违约的激励,表明相互依赖程度属于中等的非集群网络可以产生最优激励。此外,如果这个网络是集群式的,潜在的损失就不会被有偿付能力的银行完全内部化,从而导致无效率的救助水平。
卡尼克研究了银行联合行动以避免违约的激励,表明相互依赖程度属于中等的非集群网络可以产生最优激励。此外,如果这个网络是集群式的,潜在的损失就不会被有偿付能力的银行完全内部化,从而导致无效率的救助水平。
激励机制可能很复杂,因为许多不同的实体都能从避免违约中获益。例如,伯纳德等人(Bernard et al.,2017)分析了公共救助和私人自救之间的相互作用。只有当监管机构能够令人信服地承诺不干预时,才能激励私人自救,也就是说,只有在无干预且危机蔓延的范围足够有限时,才会出现私人自救。对于足够大的冲击,相互关联使监管机构在没有其他人介入的情况下进行干预符合其利益,这样就无法激励自救。此外,当且仅当银行在自救带来的收益(induced gain)中获得足够高的份额时,它们才会自救。自救带来的收益通常会扩散到整个金融体系。因此,网络越多样化,单个银行就越不愿意相互干预和救助。
金融网络一个重要且有问题的特征是它们的复杂性,这使得它们不透明。
 金融市场涉及许多不同类型的市场参与者,他们交易着各种各样的金融资产,导致了复杂多维的相互联系。此外,由于金融创新和新产品的引入是为了规避监管(Silber,1983),
金融市场涉及许多不同类型的市场参与者,他们交易着各种各样的金融资产,导致了复杂多维的相互联系。此外,由于金融创新和新产品的引入是为了规避监管(Silber,1983),
 所以这种复杂性在一定程度上是对监管的回应。重要的是,这些交易的很大一部分是在场外交易市场实现的,因此在信息不需要披露时,可能只有直接参与交易的双方知情。在缺乏完整网络数据的情况下,面对不确定的网络结构和提高透明度的成本,人们如何设计最优策略,这是拉米雷斯(Ramírez,2019)探索的一个新方向。
所以这种复杂性在一定程度上是对监管的回应。重要的是,这些交易的很大一部分是在场外交易市场实现的,因此在信息不需要披露时,可能只有直接参与交易的双方知情。在缺乏完整网络数据的情况下,面对不确定的网络结构和提高透明度的成本,人们如何设计最优策略,这是拉米雷斯(Ramírez,2019)探索的一个新方向。
即使一个人拥有某些监管辖区的所有金融机构的详细会计信息,监控金融网络的难度也会因金融体系中有更多的部分在金融监管辖区之外运作而加剧。这使得监管机构更难全面了解市场。此外,影子银行体系是内生的,它的扩张是为了回应监管体系中更严格的限制。例如,1933年《格拉斯-斯蒂格尔法案》Q条例(Regulation Q)的副作用之一就是影子银行体系的扩张,该条例禁止银行对支票账户支付利息。当利率在20世纪50年代上升时,支付利息的另类活期存款就应运而生,如储贷合一账户、货币市场存款账户,这导致投资者将他们的资本转移到影子银行体系(Lucas,2013)。一旦这些机构受到监管,不受监管的新机构就会出现,现在参与某种金融中介业务的机构种类相当庞大。
退一步说,金融监管的范围究竟应该是什么,现在还远不清楚。监管机构应该将哪些机构划定为金融机构,哪些划定为非金融机构,而后对金融机构进行监管?以大型企业和拥有大量捐赠基金的私立大学为例。它们经常同时借贷,与金融系统和实体经济相互作用。与更传统的银行一样,它们也能以类似的方式传播冲击,卷入金融传染:它们应该受到金融机构那样的监管吗?
从上文的讨论中可以清楚地看出,监管远非一刀切,最佳干预取决于许多因素,包括不断变化的网络位置和中心度。不幸的是,监管调整缓慢,而且经常受到政治的限制,因为干预可能对某些政党更有利。从历史上看,金融危机后监管激增(例如《格拉斯-斯蒂格尔法案》和《多德-弗兰克法案》),随着时间的推移,它慢慢被侵蚀,直到另一场危机袭来。
 授予央行和其他监管机构自由裁量权是避免政治周期的一种方式,但即使这种自由裁量权也会随时间而变化。事实上,这种自由裁量权往往不明确,就像2008年金融危机时那样,当时美国财政部和美联储有多大的直接干预权力并不是显而易见的。另一大挑战是建立一个灵活的监管,它能迅速适应不断变化的金融网络。
授予央行和其他监管机构自由裁量权是避免政治周期的一种方式,但即使这种自由裁量权也会随时间而变化。事实上,这种自由裁量权往往不明确,就像2008年金融危机时那样,当时美国财政部和美联储有多大的直接干预权力并不是显而易见的。另一大挑战是建立一个灵活的监管,它能迅速适应不断变化的金融网络。
(南通市金融学会 葛杨 译)
Acemoglu D, Carvalho VM, Ozdaglar A, Tahbaz-Salehi A.2012.The network origins of aggregate fluctua-tions.Econometrica 80: 1977-2016.
Acemoglu D, Ozdaglar A, Siderius J, Tahbaz-Salehi A.2020.Systemic credit freezes in financial lending networks.NBERWork.Pap.27149.
Acemoglu D, Ozdaglar A, Tahbaz-Salehi A.2015a.Systemic risk and stability in financial networks. Am.Econ.Rev. 105: 564-608.
Acemoglu D, Ozdaglar A, Tahbaz-Salehi A.2015b.Systemic risk in endogenous financial networks. Work.Pap., Mass.Inst.Technol., Cambridge.
Acharya VV, Bharath ST, Srinivasan A.2007.Does industry-wide distress affect defaulted firms? Evidence from creditor recoveries.J.Financ.Econ.85: 787-821.
Acharya VV, Yorulmazer T.2007.Toomany to fail—an analysis of time-inconsistency in bank closure poli-cies.J.Financ.Intermed.16: 1-31.
Acharya VV, Yorulmazer T.2008.Information contagion and bank herding.J.Money Credit Bank.40: 215-31.
Admati AR, Hellwig MF.2013.The Bankers'New Clothes: What's Wrong with Banking and What to Do About It.Princeton, NJ: Princeton Univ.Press.
Aikman D, Alessandri P, Eklund B, Gai P, Kapadia S, et al.2009.Funding liquidity risk in a quantita-tive model of systemic stability.In Financial Stability, Monetary Policy, and Central Banking, Vol.15, ed.R Alfaro, pp.371-410.Santiago: Cent.Bank Chile.
Aikman D, Bridges J, Kashyap A, Siegert C.2019.Would macroprudential regulation have prevented the last crisis? J.Econ.Perspect.33: 107-30.
Allen F, Babus A, Carletti E.2012.Asset commonality, debt maturity and systemic risk.J.Financ.Econ. 104: 519-34.
Allen F, Gale DM.2000.Financial contagion.J.Political Econ.108: 1-33.
Allen F, Gale DM.2007.An introduction to financial crises.Work.Pap., Wharton Financ.Inst.Cent., Univ.Pa., Philadelphia.
Allen F, Morris S, Shin HS.2006.Beauty contests and iterated expectations in asset markets. Rev.Financ.Stud.19: 719-52.
Allouch N, Jalloul M.2018.Strategic default in financial networks.Work.Pap.852, Queen Mary Univ.London, London.
Alvarez F, Barlevy G.2015.Mandatory disclosure and financial contagion.NBERWork.Pap.21328.
Amini H, Cont R, Minca A.2016.Resilience to contagion in financial networks. Math.Finance 26: 329-65.
Anderson H, Erol S, Ordoñez G.2020.Interbank networks in the shadows of the Federal Reserve Act.Work.Pap.2020-07, Fed.Depos.Insur.Corp.Cent.Financ.Res., Washington, DC.
Anderson H, Paddrik M, Wang JJ.2019.Bank networks and systemic risk: evidence from the National BankingActs.Am.Econ.Rev.109: 3125-61.
Atkisson C, Górski PJ, Jackson MO, Hołyst JA, D'Souza RM.2020.Why understanding multiplex social network structuring processes will help us better understand the evolution of human behavior.Evol.Anthropol.29: 102-7.
Babus A.2016.The formation of financial networks.RAND J.Econ.47: 239-72.
Babus A, HuTW.2017.Endogenous intermediation in over-the-counter markets.J.Financ.Econ.125: 200-15.
Banerjee AV.1992.A simple model of herd behavior.Q.J.Econ.107: 797-817.
Bardoscia M, Battiston S, Caccioli F, Caldarelli G.2017.Pathways towards instability in financial networks.Nat.Commun. 8: 14416.
Bardoscia M, Bianconi G, Ferrara G.2018.Multiplex network analysis of the UK OTC derivatives mar-ket.Staff Work.Pap.726, Bank Engl., London.
Barrot JN, Sauvagnat J.2016.Input specificity and the propagation of idiosyncratic shocks in production net-works.Q.J.Econ. 131: 1543-92.
Basel Comm.Bank.Superv.2015.Making supervisory stress tests more macroprudential: considering liquidity and solvency interactions and systemic risk.Work.Pap.29, Basel Comm.Bank.Superv., Basel, Switz.
Battiston S, Gatti DD, Gallegati M, Greenwald B, Stiglitz JE.2012.Liaisons dangereuses: increasing con-nectivity, risk sharing, and systemic risk. J.Econ.Dyn.Control 36: 1121-41.
Bebchuk LA, Goldstein I.2011.Self-fulfilling credit market freezes. Rev.Financ.Stud.24: 3519-55.
Bech ML, Atalay E.2010.The topology of the federal funds market.Phys.Stat.Mech.Appl. 389: 5223-46.
Belhaj M, Bourlès R, Deroïan F.2020.Prudential regulation in financial networks.Work.Pap.30, Aix-Marseille Sch.Econ., Marseille, Fr.
Bernard B, Capponi A, Stiglitz JE.2017.Bail-ins and bail-outs: incentives, connectivity, and systemic stability.NBER Work.Pap.23747.
Bikhchandani S, Hirshleifer D, Welch I.1992.A theory of fads, fashion, custom, and cultural change as informational cascades.J.Political Econ.100: 992-1026.
Billio M, Getmansky M, Lo AW, Pelizzon L.2012.Econometric measures of connectedness and systemic risk in the finance and insurance sectors.J.Financ.Econ.104: 535-59.
Blasques F, Bräuning F, Van Lelyveld I.2018.A dynamic network model of the unsecured interbank lend-ing market.J.Econ.Dyn.Control 90: 310-42.
Branch B.2002.The costs of bankruptcy: a review.Int.Rev.Financ.Anal.11: 39-57.
Bruche M, Gonzalez-Aguado C.2010.Recovery rates, default probabilities, and the credit cycle.J.Bank.Finance 34: 754-64.
Brunnermeier MK.2009.Deciphering the liquidity and credit crunch 2007-2008. J.Econ.Perspect. 23: 77-100.
Brusco S, Castiglionesi F.2007.Liquidity coinsurance, moral hazard, and financial contagion.J.Finance 62: 2275-302.
Brusco S, Jackson MO.1999.The optimal design of a market.J.Econ.Theory 88: 1-39.
Burkholz R, Leduc MV, Garas A, Schweitzer F.2016.Systemic risk in multiplex networks with asymmetric coupling and threshold feedback.Phys.D 323: 64-72.
Caballero RJ, Simsek A.2013.Fire sales in a model of complexity. J.Finance 68: 2549-87.
Cabrales A, Gottardi P, Vega-Redondo F.2017.Risk sharing and contagion in networks.Rev.Financ. Stud.30: 3086-127.
Callaway DS, Newman ME, Strogatz SH, Watts DJ.2000.Network robustness and fragility: percolation on random graphs.Phys.Rev.Lett. 85: 5468.
Calomiris CW, JaremskiM.2019.Stealing deposits: deposit insurance, risk-taking, and the removal of market discipline in early 20th-century banks.J.Finance 74: 711-54.
Capponi A, Chen PC.2015.Systemic risk mitigation in financial networks.J.Econ.Dyn.Control 58: 152-66.
Capponi A, Cheng WA.2018.Clearinghouse margin requirements.Oper.Res.66: 1542-58.
Capponi A, Corell FC, Stiglitz JE.2020.Optimal bailouts and the doom loop with a financial net-work.NBER Work.Pap.27074.
Capponi A, LarssonM.2015.Price contagion through balance sheet linkages.Rev.Asset Pricing Stud.5: 227-53.
CentolaD.2018.How Behavior Spreads: The Science of Complex Contagions.Princeton, NJ: PrincetonUniv. Press.
Chincarini LB.2012.The Crisis of Crowding: Quant Copycats, UglyModels, and the New Crash Normal. New York: Wiley.
Cifuentes R, Ferrucci G, Shin HS.2005.Liquidity risk and contagion.J.Eur.Econ.Assoc. 3: 556-66.
Cohen-Cole E, Patacchini E, Zenou Y.2015.Static and dynamic networks in interbank markets. Netw.Sci.3: 98-123.
Covi G, Gorpe MZ, Kok C.2019.Comap: mapping contagion in the euro area banking sector.Work.Pap.2224, Eur.Cent.Bank, Frankfurt, Ger.
Craig B, Von Peter G.2014.Interbank tiering and money center banks.J.Financ.Int. 23: 322-47.
Csóka P, Herings PJJ.2018.Decentralized clearing in financial networks.Manag.Sci.64 (10): 4681-99.
Dam L, KoetterM.2012.Bank bailouts and moral hazard: evidence fromGermany.Rev.Financ.Stud. 25: 2343-80.
Davydenko SA, Strebulaev IA, Zhao X.2012.A market-based study of the cost of default.Rev.Financ. Stud.25: 2959-99.
Demange G.2016.Contagion in financial networks: a threat index.Manag.Sci.64: 955-70.
Demsetz H.1968.The cost of transacting.Q.J.Econ.82: 33-53.
D'Errico M, Roukny T.2019.Compressing over-the-counter markets.arXiv: 1705.07155[q-fin.GN].
Diamond DW.1991.Monitoring and reputation: the choice between bank loans and directly placed debt.J.Political Econ. 99: 689-721.
Diamond DW, Dybvig PH.1983.Bank runs, deposit insurance, and liquidity.J.Political Econ.91: 401-19.
Diamond DW, Rajan RG.2011.Fear of fire sales, illiquidity seeking, and credit freezes.Q.J.Econ. 126: 557-91.
Diebold FX, Yılmaz K.2014.On the network topology of variance decompositions: measuring the connected-ness of financial firms.J.Econom.182: 119-34.
Duarte F, Eisenbach TM.2018.Fire-sale spillovers and systemic risk.Staff Rep., Fed.Reserve Bank New York, New York.
Duarte F, Jones C.2017.Empirical network contagion for U.S.financial institutions.Staff Rep., Fed.Reserve Bank New York, New York.
Duffie D.2019.Prone to fail: the pre-crisis financial system.J.Econ.Perspect.33: 81-106.
Duffie D, Eckner A, Horel G, Saita L.2009.Frailty correlated default.J.Finance 64: 2089-123.
Duffie D, Wang C.2016.Efficient contracting in network financial markets.Work.Pap., Stanford Univ., Stanford, CA.
Duffie D, Zhu H.2011.Does a central clearing counterparty reduce counterparty risk? Rev.Asset Pricing Stud.1: 74-95.
Eisenberg L, Noe TH.2001.Systemic risk in financial systems.Manag.Sci.47: 236-49.
Elliott M, Georg CP, Hazell J.2018.Systemic risk-shifting in financial networks.Work.Pap., Univ. Cam-bridge, Cambridge, UK.
Elliott M, Golub B, Jackson MO.2014.Financial networks and contagion.Am.Econ.Rev. 104: 3115-53.
Engle RF, Ruan T.2019.Measuring the probability of a financial crisis.PNAS 116: 18341-46.
Erol S.2019.Network hazard and bailouts.Work.Pap., Carnegie Mellon Univ., Pittsburgh, PA.
Erol S, Vohra R.2018.Network formation and systemic risk.Work.Pap., Univ.Pa., Philadelphia.
Etessami K, Papadimitriou C, Rubinstein A, Yannakakis M.2019.Tarski's theorem, supermodular games, and the complexity of equilibria.arXiv: 1909.03210[cs.CC].
Farboodi M.2017.Intermediation and voluntary exposure to counterparty risk.Work.Pap., Princeton Univ., Princeton, NJ.
Farmer JD, Kleinnijenhuis AM, Nahai-Williamson P, Wetzer T.2020.Foundations of system-wide finan-cial stress testing with heterogeneous institutions.StaffWork.Pap.861, Bank Engl., London.
Ferrara G, Langfield S, Liu Z, Ota T.2017.Systemic illiquidity in the interbank network.Staff Work.Pap.586, Bank Engl., London.
Financ.Crisis Inq.Comm.2011.The Financial Crisis Inquiry Report.Washington, DC: US Gov.Print.Off.
Fleming MJ, Sarkar A.2014.The failure resolution of Lehman Brothers.Econ.Policy Rev., Fed.Reserve Bank New York, New York.
Fostel A, Geanakoplos J.2008.Leverage cycles and the anxious economy.Am.Econ.Rev. 98: 1211-44.
Fostel A, Geanakoplos J.2014.Endogenous collateral constraints and the leverage cycle.Annu.Rev.Econ.6: 771-99.
Fricke D, Wilke H.2020.Connected funds.Dtsch.Bundesbank Discuss.Pap.48, Frankfurt, Ger.
Gai P, Haldane A, Kapadia S.2011.Complexity, concentration and contagion.J.Monet.Econ. 58: 453-70.
Gai P, Kapadia S.2010.Contagion in financial networks. Proc.R.Soc.A 466: 2401-23.
Gale DM, Kariv S.2007.Financial networks.Am.Econ.Rev.97: 99-103.
Galeotti A, Ghiglino C.2021.Cross-ownership and portfolio choice.J.Econ.Theory 192: 105194.
Garas A.2016.Interconnected Networks.New York: Springer.
Gehrig T.1993.Intermediation in search markets.J.Econ.Manag.Strategy 2: 97-120.
Glasserman P, Young HP.2015.How likely is contagion in financial networks? J.Bank.Finance 50: 383-99.
Glasserman P, Young HP.2016.Contagion in financial networks.J.Econ.Lit. 54 (3): 779-831.
Glode V, Opp C.2016.Asymmetric information and intermediation chains.Am.Econ.Rev. 106: 2699-721.
Glode V, Opp CC, Zhang X.2019.On the efficiency of long intermediation chains. J.Financ.Int. 38: 11-18.
Godlewski CJ, Sanditov B.2018.Financial institutions network and the certification value of bank loans.Financ.Manag.47: 253-83.
Godlewski CJ, Sanditov B, Burger-Helmchen T.2012.Bank lending networks, experience, reputation, and borrowing costs: empirical evidence from the French syndicated lending market.J.Bus.Finance Account.39: 113-40.
Gofman M.2017.Efficiency and stability of a financial architecture with too-interconnected-to-fail institutions.J.Financ.Econ.124: 113-46.
Greenwood R, Landier A, Thesmar D.2015.Vulnerable banks.J.Financ.Econ.115: 471-85.
Gualdi S, Cimini G, Primicerio K, Di Clemente R, Challet D.2016.Statistically validated network of portfolio overlaps and systemic risk.Sci.Rep.6: 39467.
Haldane AG.2009.Rethinking the financial network.Speech delivered at the Financial Student Association, Amsterdam, The Netherlands, April 28.
Hastings M, Hemenway Falk B, Tsoukalas G.2020.Privacy-preserving network analytics.Work.Pap., Univ.Pa., Philadelphia.
Hauton G, Héam JC.2016.How to measure interconnectedness between banks, insurers and financial con-glomerates. Stat.Risk Model.33: 95-116.
Heipertz J, Ouazad A, Rancière R.2019.The transmission of shocks in endogenous financial networks: a structural approach.NBER Work.Pap.26049.
Herskovic B.2018.Networks in production: asset pricing implications.J.Finance 73: 1785-818.
HirshleiferD, Teoh SH.2009.Systemic risk, coordination failures, and preparedness externalities: applica-tions to tax and accounting policy. J.Financ.Econ.Policy 1: 128-42.
Holmstrom B, Tirole J.1997.Financial intermediation, loanable funds, and the real sector.Q.J.Econ. 112: 663-91.
Ibragimov R, Jaffee D, Walden J.2011.Diversification disasters.J.Financ.Econ. 99: 333-48.
Infante S, Vardoulakis A.2018.Collateral runs.Finance Econ.Discuss.Ser.2018-022, Board Gov.Fed. Reserve Syst., Washington, DC.
Jackson MO.2008.Social and Economic Networks. Princeton, NJ: Princeton Univ.Press.
Jackson MO.2019.The Human Network: How Your Social Position Determines Your Power, Beliefs and Be-haviors. New York: Pantheon.
Jackson MO, Nei S.2015.Networks of military alliances, wars, and international trade.PNAS 112: 15277-84.
Jackson MO, Pernoud A.2019.Distorted investment incentives, regulation, and equilibrium multiplicity in a model of financial networks.Work.Pap., Stanford Univ., Stanford, CA.
Jackson MO, Pernoud A.2020.Credit freezes, equilibrium multiplicity, and optimal bailouts in financial networks.Work.Pap., Stanford Univ., Stanford, CA.
Jackson MO, Storms EC.2017.Behavioral communities and the atomic structure of networks.arXiv: 1710.04656[physics.soc-ph].
Jackson MO, Wolinsky A.1996.A strategic model of social and economic networks.J.Econ.Theory 71: 44-74.
James C.1991.The losses realized in bank failures. J.Finance 46: 1223-42.
Jensen MC, MecklingWH.1976.Theory of the firm: managerial behavior, agency costs and ownership structure.J.Financ.Econ. 3: 305-60.
Kanik Z.2019.From Lombard Street to Wall Street: systemic risk, rescues, and stability in financial net-works.Work.Pap., Mass.Inst.Technol., Cambridge.
Karamysheva M, Seregina E.2020.Prudential policies and systemic risk: the role of interconnections.Work. Pap., HSE Univ., Moscow.
Keynes JM.1936.The General Theory of Employment, Interest, and Money. London: Macmillan.
King MA, Wadhwani S.1990.Transmission of volatility between stock markets.Rev.Financ.Stud.3: 5-33.
Kivela M, Arenas A, Gleeson JP, Moreno Y, Porter MA.2014.Multilayer networks.arXiv: 1309.7233v4[physics.soc-ph].
Kiyotaki N, Moore J.1997.Credit cycles.J.Political Econ.105: 211-48.
Klasing MJ, Milionis P.2014.Quantifying the evolution of world trade, 1870-1949.J.Int.Econ.92: 185-97.
Krishnamurthy A.2010.Amplification mechanisms in liquidity crises.Am.Econ.J.Macroecon.2: 1-30.
Leitner Y.2005.Financial networks: contagion, commitment, and private sector bailouts.J.Finance 60: 2925-53.
Lucas D.2019.Measuring the cost of bailouts.Annu.Rev.Econ.11: 85-108.
Lucas RE Jr.2013.Glass-Steagall: a requiem.Am.Econ.Rev.103: 43-47.
Lund S, Härle P.2017.Global finance resets.Finance Dev.54: 42-44.
Malherbe F.2014.Self-fulfilling liquidity dry-ups.J.Finance 69: 947-70.
Martínez J - F, Peiris MU, Tsomocos DP.2020.Macroprudential policy analysis in an estimated DSGE model with a heterogeneous banking system: an application to Chile.Work.Pap., HSE Univ., Moscow.
Morris S, Shin HS.1998.Unique equilibrium in a model of self-fulfilling currency attacks.Am.Econ.Rev. 88: 587-97.
Morris S, Shin HS.2002.Social value of public information.Am.Econ.Rev. 92: 1521-34.
Nanumyan V, Garas A, Schweitzer F.2015.The network of counterparty risk: analysing correlations in OTC derivatives.PLOS ONE 10: e0136638.
O'Hara M.1997. Market Microstructure Theory. Oxford, UK: Blackwell.
Rajan RG.1992.Insiders and outsiders: the choice between informed and arm's-length debt.J.Finance 47: 1367-400.
Ramírez C.2017.Firm networks and asset returns.Finance Econ.Discuss.Ser.2017 - 014, Board Gov.Fed.Reserve Syst., Washington, DC.
Ramírez C.2019.Regulating financial networks under uncertainty.Finance Econ.Discuss.Ser.2019 -056, Board Gov.Fed.Reserve Syst., Washington, DC.
Reinhart C, Rogoff K.2009.This Time Is Different. Princeton, NJ: Princeton Univ.Press.
Rochet JC, Tirole J.1996.Interbank lending and systemic risk.J.Money Credit Bank.28 (4): 733-62.
Rogers LC, Veraart LA.2013.Failure and rescue in an interbank network.Manag.Sci.59: 882-98.
Roukny T, Battiston S, Stiglitz JE.2018.Interconnectedness as a source of uncertainty in systemic risk.J.Financ.Stab. 35: 93-106.
Scharfstein DS, Stein JC.1990.Herd behavior and investment.Am.Econ.Rev. 80: 465-79.
Shell K.1989.Sunspot equilibrium.In General Equilibrium, ed.J Eatwell, M Milgate, P Newman, pp.274-80.New York: Springer.
Shiller RJ.2015.Irrational Exuberance. Princeton, NJ: Princeton Univ.Press.3rd ed.
Shu C.2019.Endogenous risk - exposure and systemic instability.USC-INET Res.Pap.17 -35, Univ. South.Calif., Los Angeles.
Siebenbrunner C.2021.Quantifying the importance of different contagion channels as sources of systemic risk.J.Econ.Interact.Coord.16: 103-31.
Silber WL.1983.The process of financial innovation.Am.Econ.Rev.73: 89-95.
Soramäki K, Bech ML, Arnold J, Glass RJ, Beyeler WE.2007.The topology of interbank payment flows.Phys.A 379: 317-33.
Spulber DF.1996.Market microstructure and intermediation.J.Econ.Perspect. 10: 135-52.
Stellian R, Penagos GI, Danna-Buitrago JP.2021.Firms in financial distress: evidence from inter -firm payment networks with volatility driven by“animal spirits.”J.Econ.Interact.Coord. 16: 59-101.
Summer M.2013.Financial contagion and network analysis.Annu.Rev.Financ.Econ.5: 277-97.
Tarullo DK.2019.Financial regulation: still unsettled a decade after the crisis.J.Econ.Perspect.33: 61-80.
Teteryatnikova M.2014.Systemic risk in banking networks: advantages of tiered banking systems.J.Econ. Dyn.Control 47: 186-210.
Upper C, Worms A.2004.Estimating bilateral exposures in the German interbank market: Is there a danger of contagion? Eur.Econ.Rev. 48: 827-49.
Wagner W.2010.Diversification at financial institutions and systemic crises. J.Financ.Intermed.19: 373-86.
Wang C.2017.Core-periphery trading networks.PhD Thesis, Stanford Univ., Stanford, CA.
Wang JJ, Capponi A, Zhang H.2020.A theory of collateral requirements for central counterparties.Work.Pap., Ariz.State Univ., Tempe.
Yellen J.2013.Interconnectedness and systemic risk: lessons from the financial crisis and policy implica-tions: a speech at the American Economic Association/American Finance Association.
Joint Luncheon, San Diego, California, January 4, 2013.Speech 631, Board Gov.Fed.Reserve Syst., Washington, DC.
[1] 也就是说,如果对于所有的i有V i ′≥V i ,那么有F(V′|G)≥F(V|G),且可行V的集合是上下有界的。
[2] 最好均衡和最坏均衡可通过一个简单算法找到:从可能的最大值V max 开始(或从最小值开始找最坏均衡),然后通过函数F迭代。在许多金融模型中,随着基础资产价值对方程的驱动,收敛速度很快(参见Eisenberg and Noe,2001;Jackson and Pernoud,2020),而对于那些相互依赖性更任意的模型,找到均衡的速度可能慢得多(参见Etessami et al.,2019)。