2.1 SNSV方程的全局吸引子

本节研究随机Navier-Stokes-Voight方程的解的适定性，并证明方程存在全局随机吸引子.

2.1.1 模型和一些记号

我们研究下列三维随机Navier-Stokes-Voight (SNSV)方程：

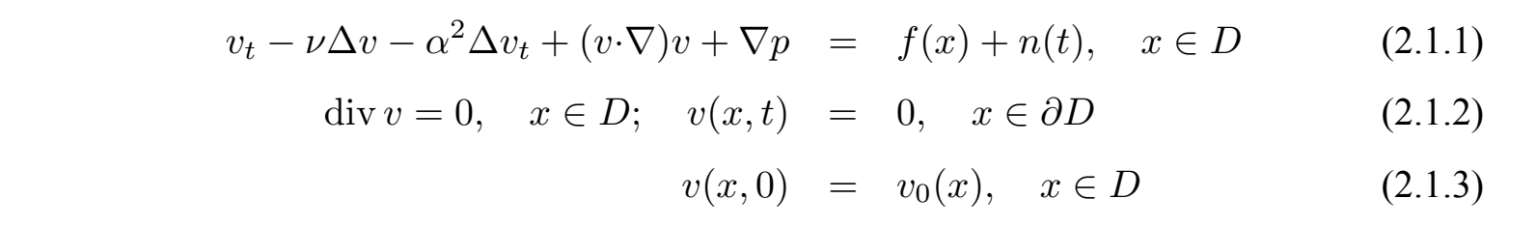
其中D ⊂ 是带有光滑边界∂D的有界区域，v=v(x，t)是速度向量，p是压力项，ν>0是kinematic黏性系数，α是表示流体弹性的长度参数，f是给定的外力场，n(t)是随机力场，记作 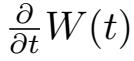.我们假设W(t)是H-值无限维布朗运动，具有形式

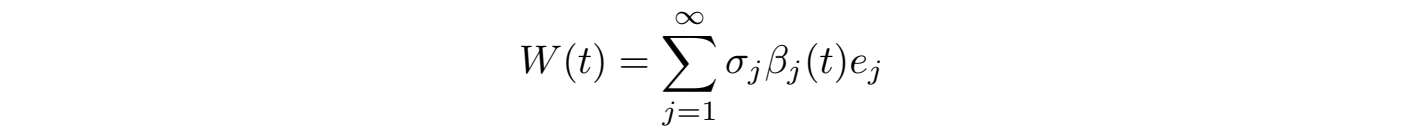
其中 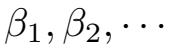是完备概率空间(Ω，F，P)上的一列独立标准布朗运动(期望记作 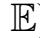)， 是标准正交基.

本节我们用到以下数学记号：

·L ^p (D)，1⩽p⩽∞和H ^s (D)分别是通常的Lebesgue和Sobolev空间.

·对v=(v ₁ ，v ₂ ，v ₃ )和u=(u ₁ ，u ₂ ，u ₃ )，我们记

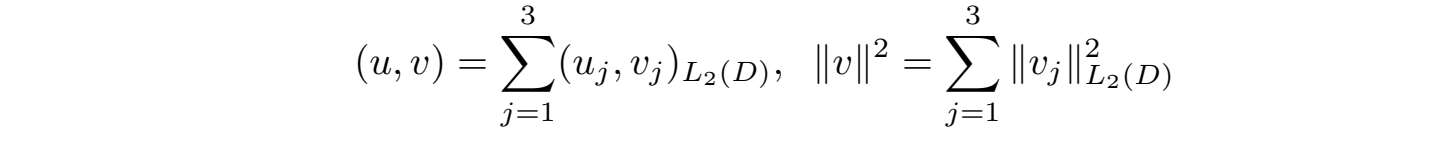
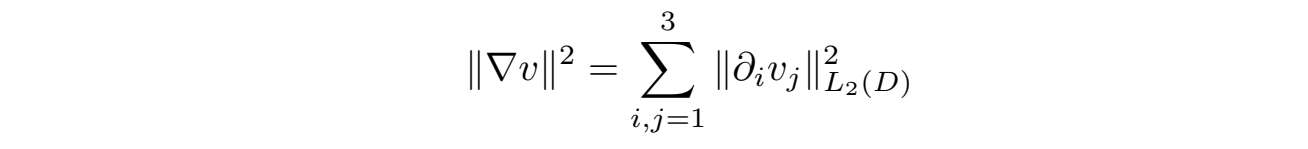
·记

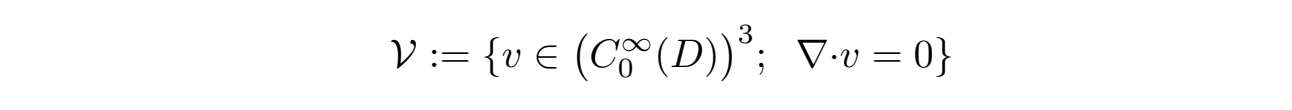
·H是集合V按(L ₂ (D) ^{3 )} 范数的闭包.

·P是从( L ₂ (D) ^{3 )} 到空间H的Helmholz-Leray正交投影.

·A：=−P ∆是定义在 H ₂ (D) ³ ∩ V上满足齐次Dirichlet边界条件的Stokes算子.算子A是空间H的正定自伴算子，其逆算子A−1是从H到H的紧算子.

·我们记 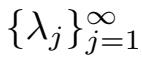，0 < 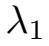⩽ ⩽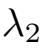···是Stokes算子A的特征函数 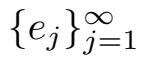对应的特征值.

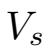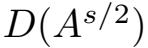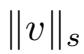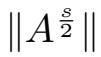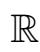· ：= ， = ，s∈ . V= 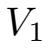= 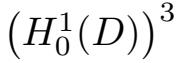∩ H是Hilbert空间，运用Poincaré不等式，有 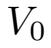=H.

·对u，v，w∈V，我们定义下面双线性形式

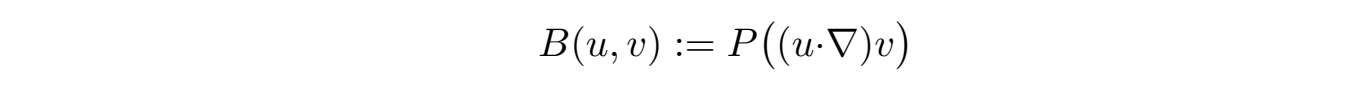
和三线性形式

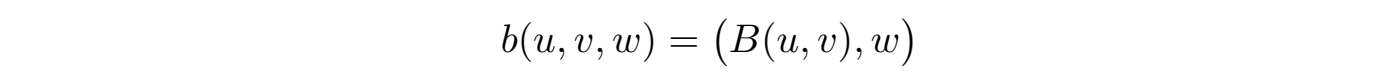
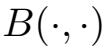可以看成V×V→ 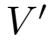的连续算子，其中 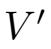是V的对偶空间(见文献[82]).

·对任意u，v，w∈V，有

2.1.2 SNSV方程的适定性

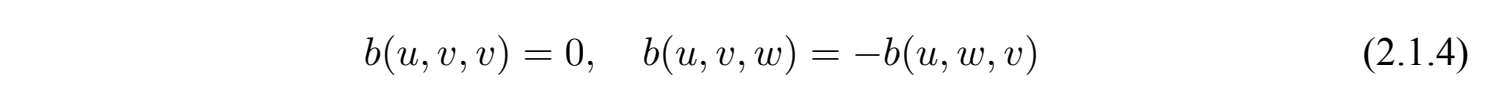
将SNSV方程的每一项通过Helmholz-Leray正交投影到散度为零的空间中，这样项∇p将会消失，为了书写方便，我们把P f和P n仍然记作f和n，这样得到下列方程：

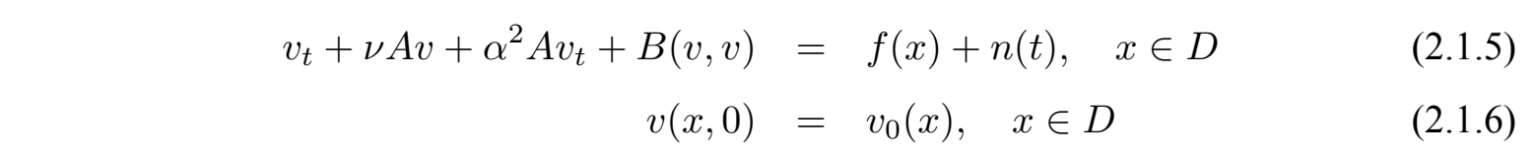
不失一般性，我们令α=1.

下面我们研究上述方程解的存在性和唯一性，考虑下列辅助方程：

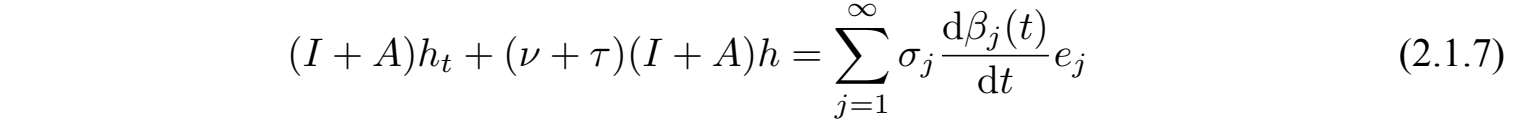
不难看出算子(I+A)是正定自伴的，其逆算子(I+A)−1存在且是紧的，满足 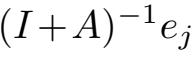= 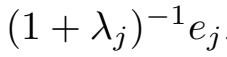.这样方程(2.1.7)的形式等价于下列Ornstein-Uhlenbeck方程：

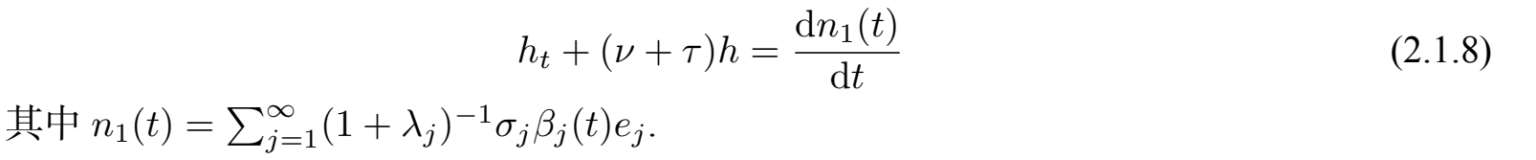
因为W(t)是H-值的Wiener过程，我们有 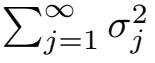< ∞，从而

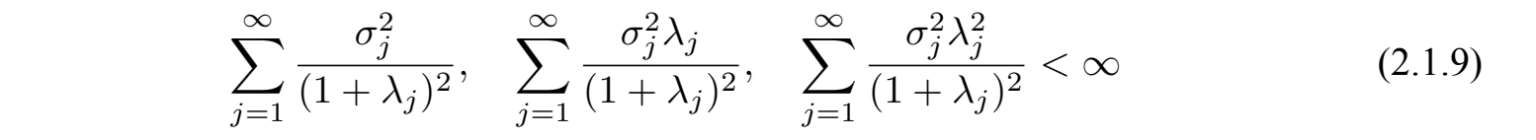
从文献[83]可知，过程

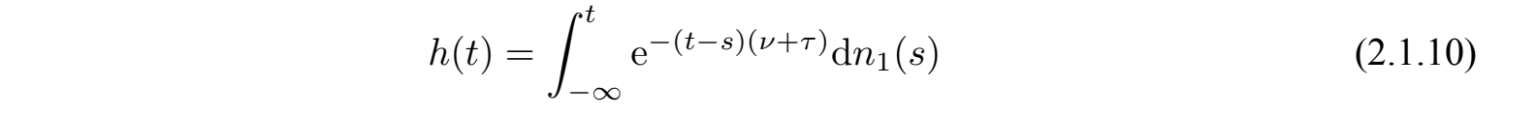
取值于D(A)有连续轨道的稳定遍历的解.特别地，运用(2.1.9)，有

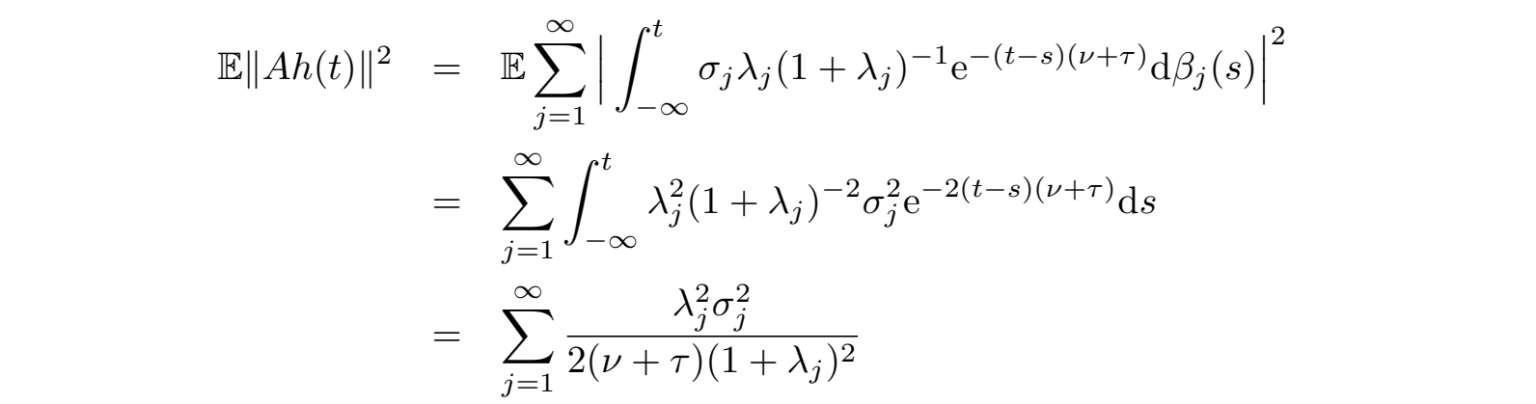
是有限的.类似的，我们有

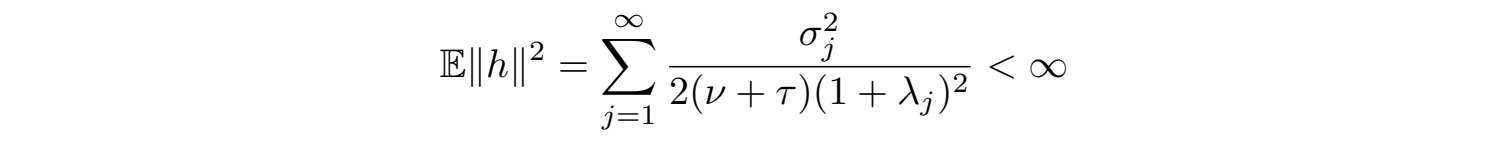
和

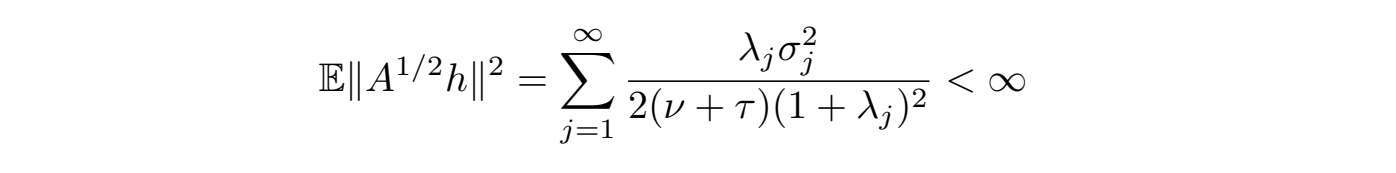
注 2.1： 需要特别指出，因为我们在Navier-Stokes方程上加了正则项 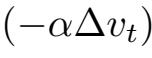，从而形成 了SNSV方程，这里我们仅仅需要假设W(t)是H-值的布朗运动，相比于H. Crauel、A. Debussche和F. Flandoli ^[15] 条件更弱，在文献[15]中，W(t)需要是D(A)-值的布朗运动.

通过变换u(t)=v(t)−h(t)，得到u(t，x)满足下面随机系数方程

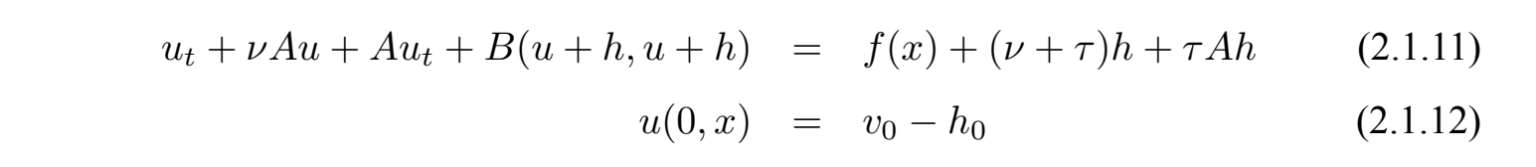
我们接下来给出方程(2.1.11)～(2.1.11)的解的适定性，在此之前先给出解的定义.

定义2.1.1 函数u∈C([0，T]，V )称为方程(2.1.11)～(2.1.11)的弱解，若满足对∀v∈V，有

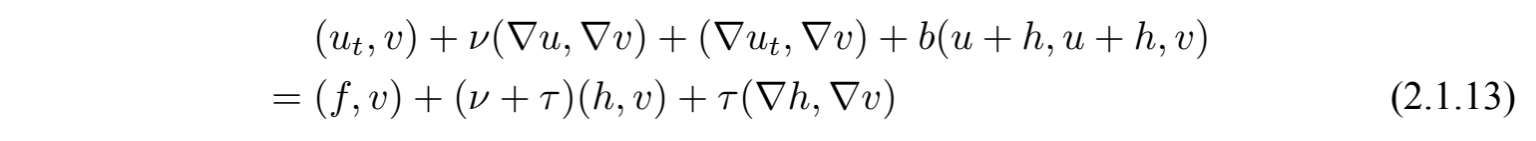
成立.

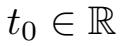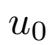定理2.1.1 假设 和 ∈V，对 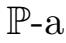. e. ω∈Ω，下列结论成立：

(i)在时间[t ₀ ，∞)上，方程(2.1.11)～(2.1.12)存在唯一解，满足u∈C[t ₀ ，∞)，V .

(ii)记解为u(t，ω；t ₀ ，u ₀ )，映射u ₀ 7→u(t，ω；t ₀ ，u ₀ )对t⩾t ₀ 是连续的.

证明 ：我们应用Feado-Galerkin方法，记m是任意给定的正数.对每一个m，方程(2.1.13)的逼近解u _m 满足

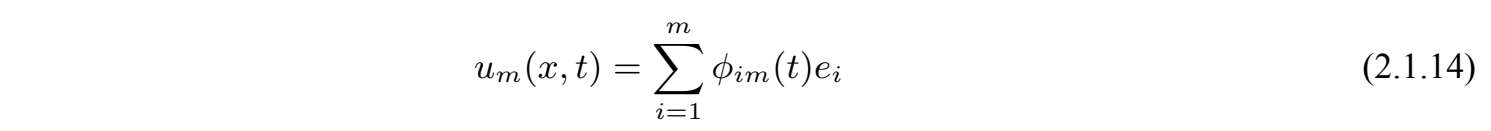
则有

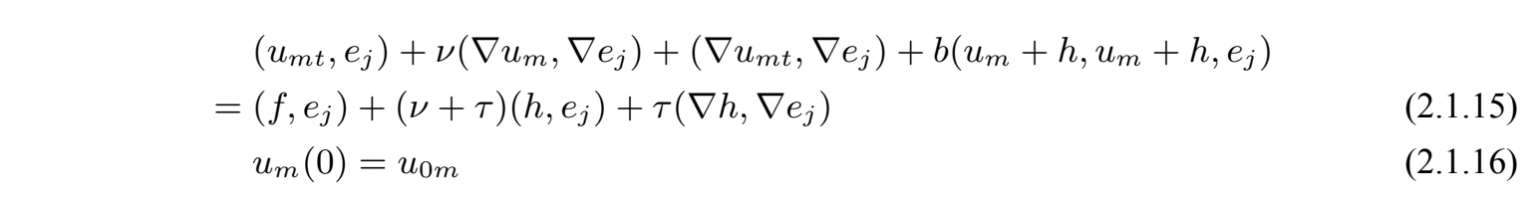
其中u _{0 m} 是V中的u ₀ 到由e1，···，e _m 张成的有限维空间上的正交投影，满足当m→∞时，u _{0 m} 强收敛于u ₀ .系统(2.1.15)形成了函数ϕ _{1 m} ，···，ϕ _mm 的一阶常微分方程，有

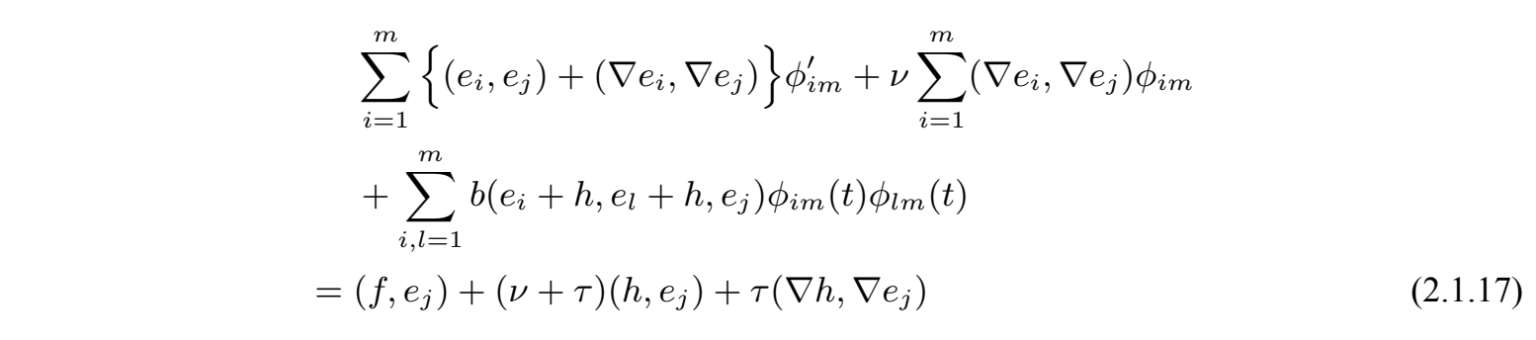
矩阵的元素a _ij 满足

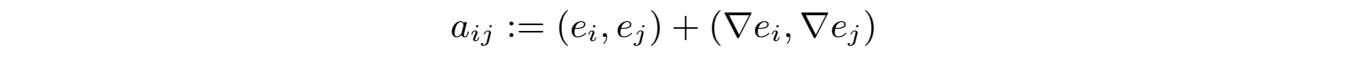
或

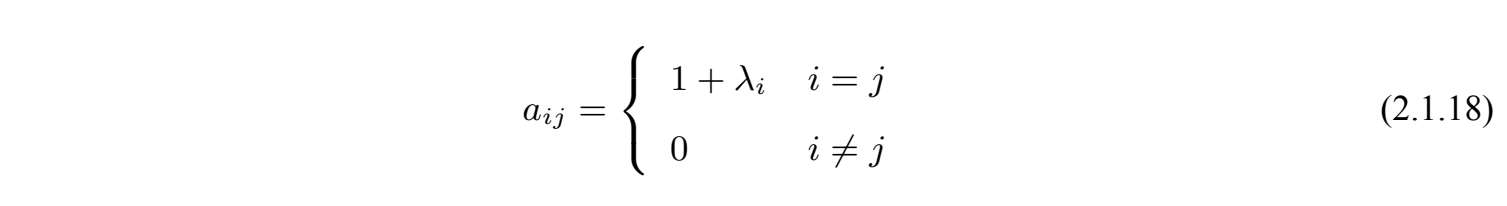
该矩阵是可逆的(见文献[84，引理3]).为此我们得到方程

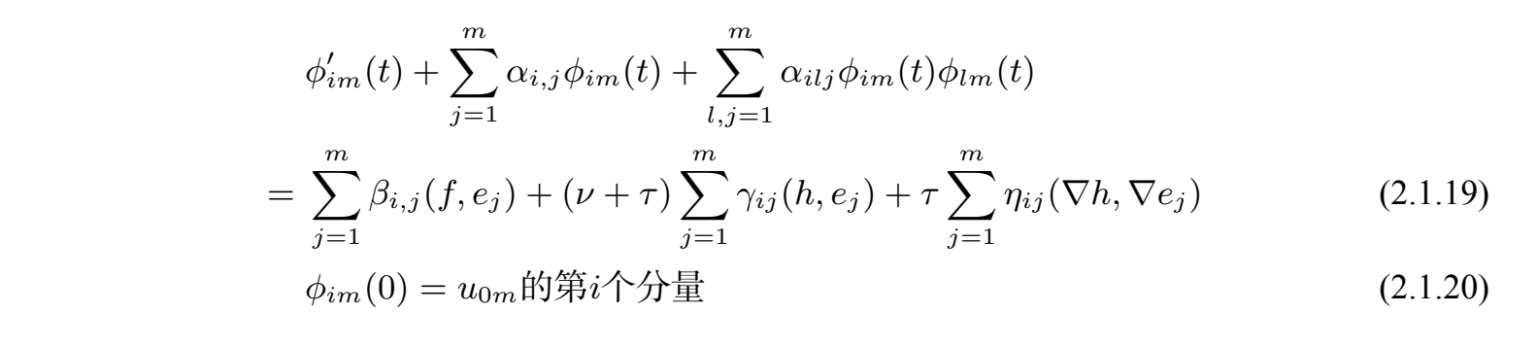
其中 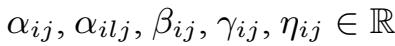.由常微分方程理论，在某个时间段[0，T]上，这个方程存在最大解.

下面我们将得到 的一些先验估计.估计 ∈ 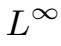(0，T；V )∩ 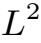(0，T；V )将在下节给出，这里先给出 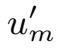∈ 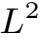(0，T；V )的估计.

在方程(2.1.15)上乘以 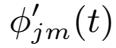并对j=1，···，m，求和，我们有

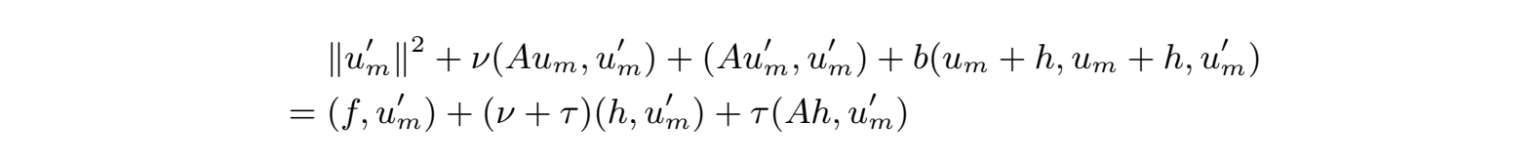
然后我们得到

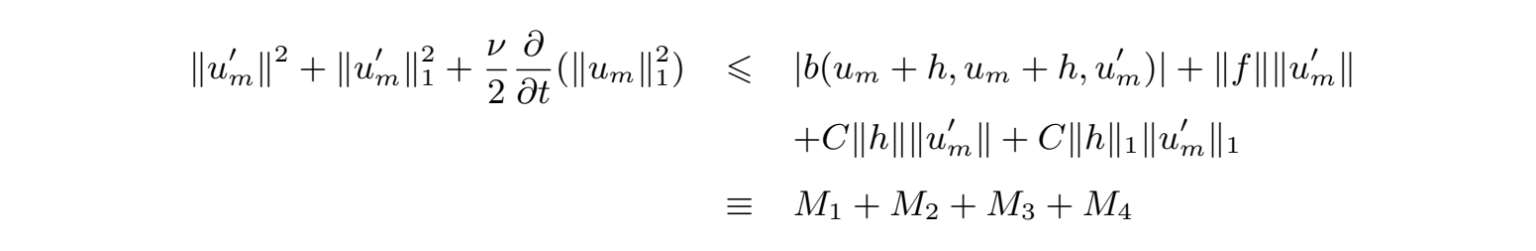
运用(2.1.4)、Hölder不等式、Ladyzhenskaya不等式 ^{[82，85，86]} 、Sobolev不等式 ^[87] 和Young不等式，推出

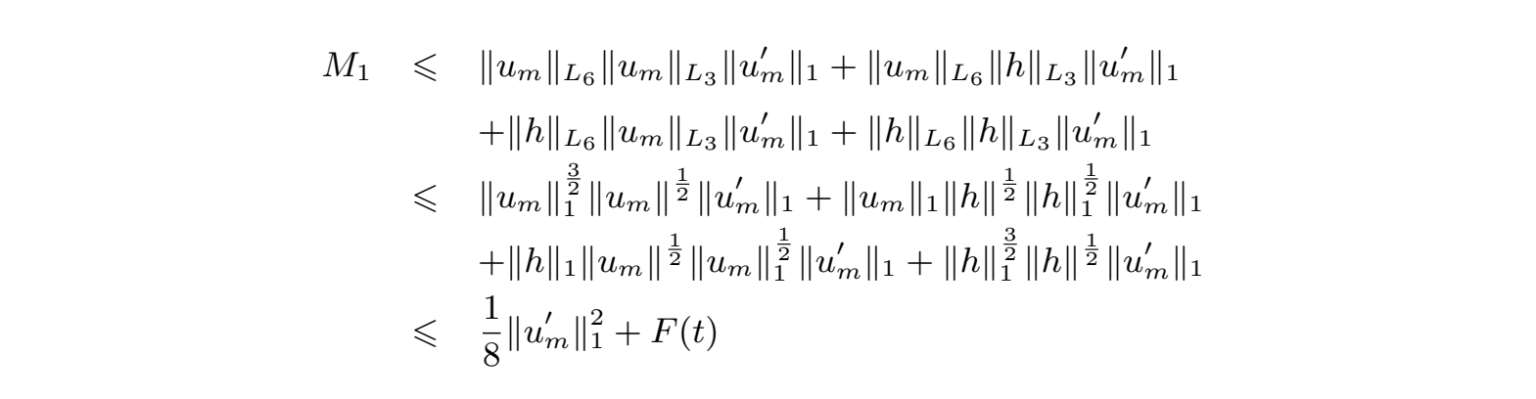
和

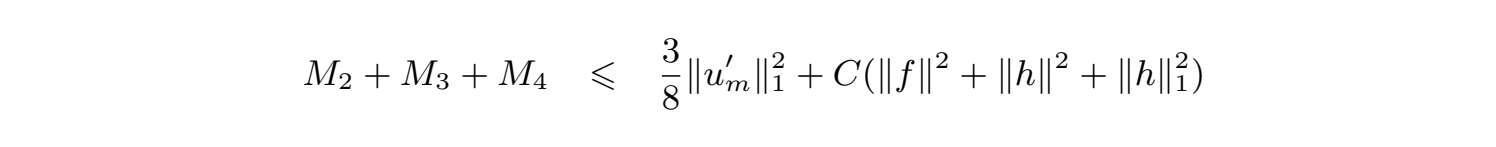
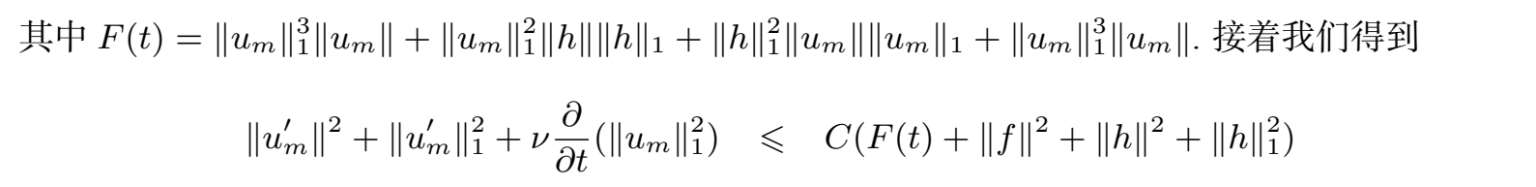
对上式关于时间积分，

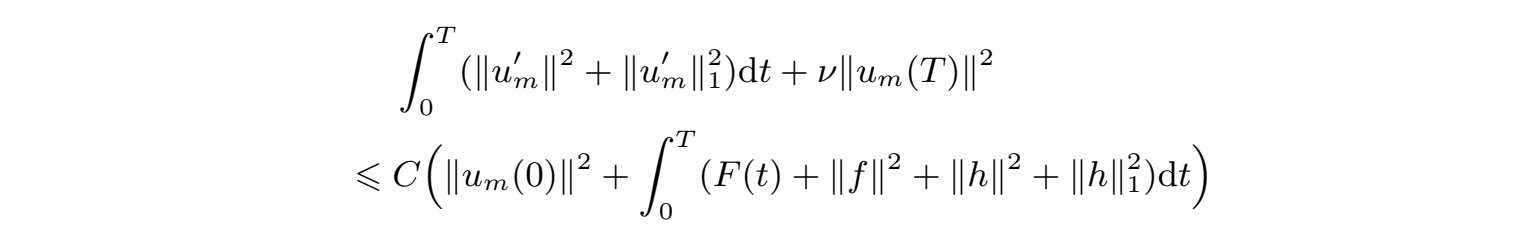
因为 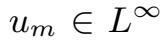(0，T；V )∩ 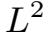(0，T；V )且 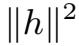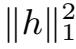， 是有限的，可以推出 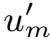∈ 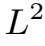(0，T；V ).从而有 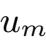∈ 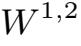(0，T；V )⊂ C([0，T]，V ).令m→∞，我们得到了方程(2.1.13)存在一弱解.

唯一性的证明是经典的：假设 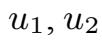具有相同初值方程(2.1.11)的解，令U(t)= 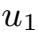− 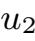，则U(t)满足方程

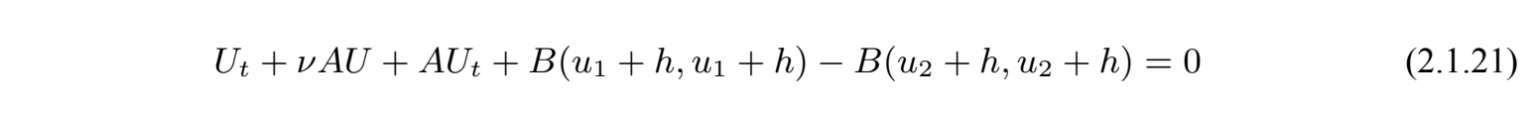
方程两边关于U(t)做内积，运用(2.1.4)、Hölder不等式、Ladyzhenskaya不等式、Sobolev不等式和Young不等式，有

可以推出

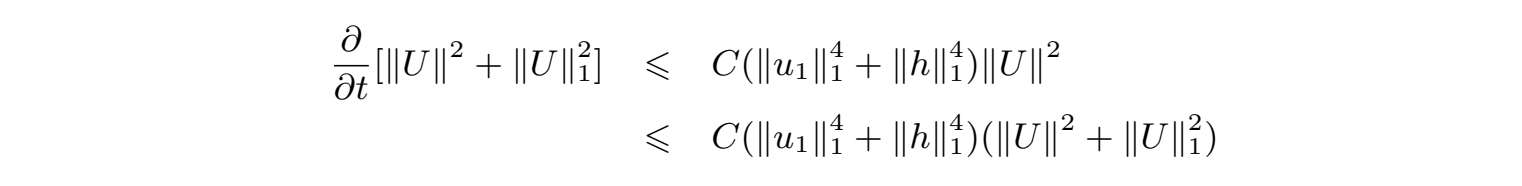
应用Gronwall引理，我们推出方程解的唯一性，同时得到u(t)∈V连续依赖初值.

由映射 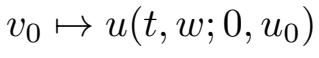+h(t，w)可以定义一随机流函数ϕ(t，w)，其满足

2.1.3 SNSV方程的全局吸引子

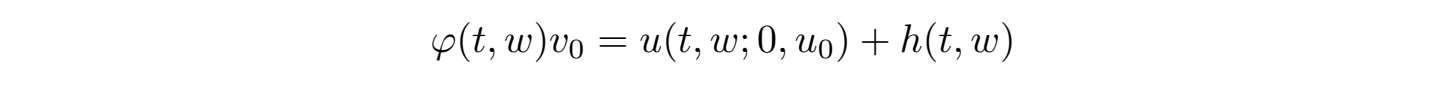
下面证明在0时刻存在随机吸收集K(w).令B是V中的有界集，对 ，u是方程(2.1.11)～(2.1.12)的解且u _s =v _s −h(s，w).

对方程(2.1.11)关于u做内积，得到

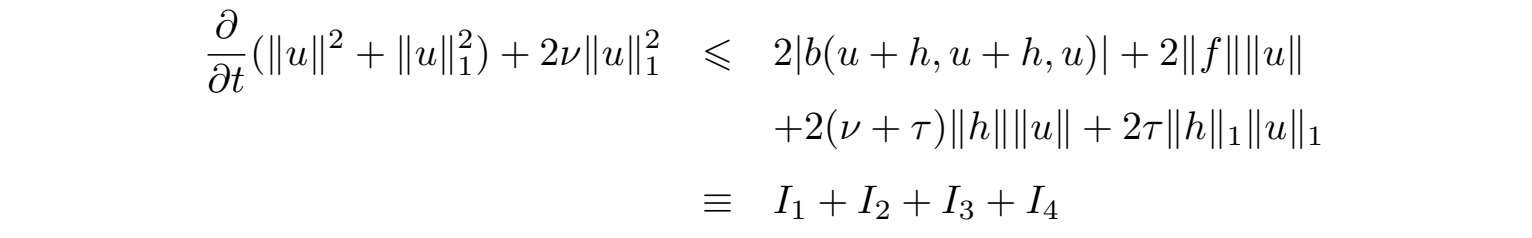
运用(2.1.4)、Hölder不等式、Ladyzhenskaya不等式、Sobolev不等式和Young不等式，可得

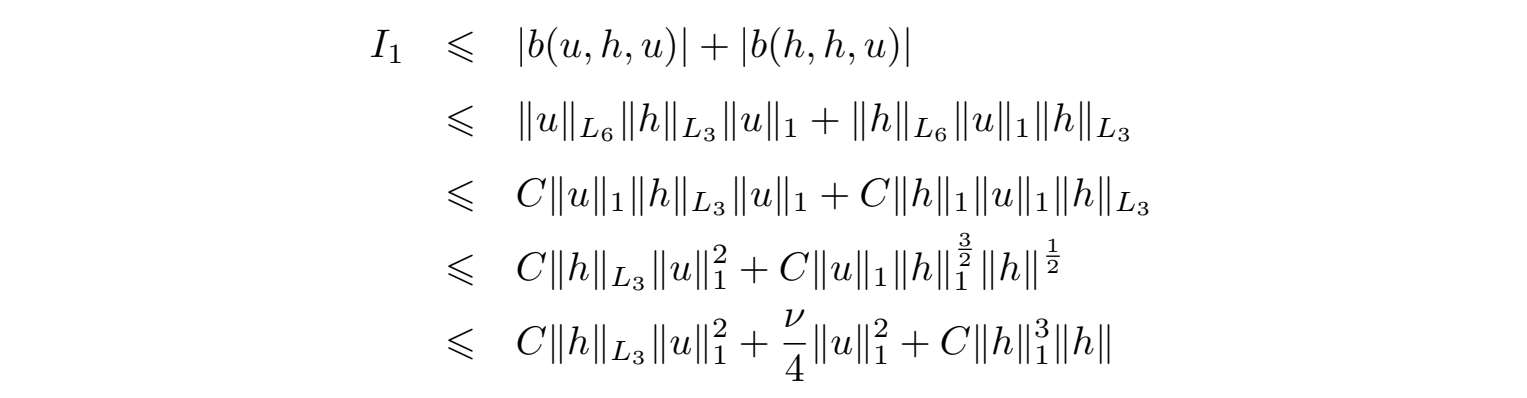
和

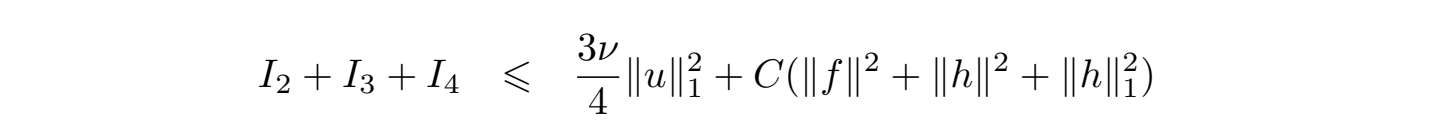
我们得出

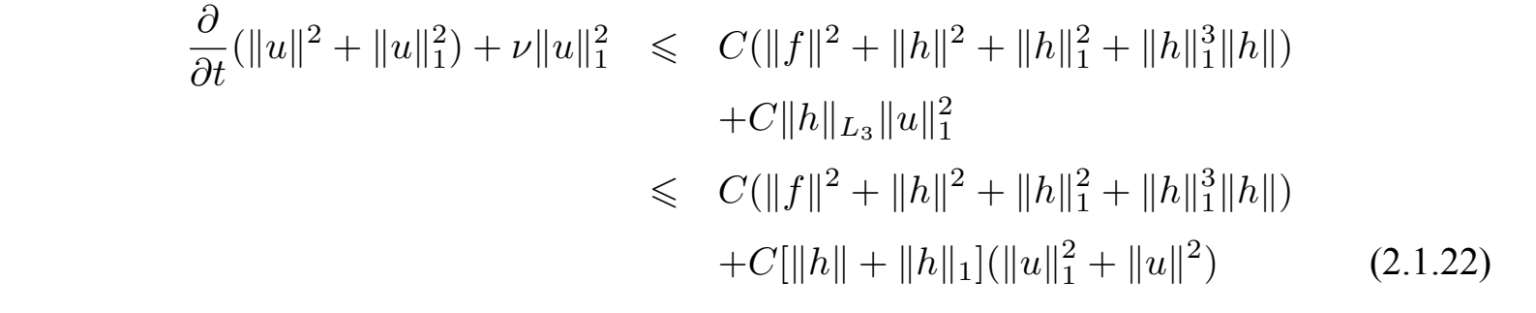
由Poincaré不等式不难看出

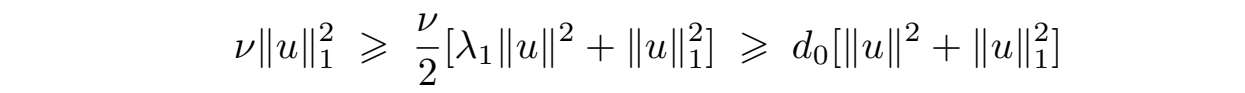
其中 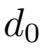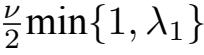：= ，由(2.1.22)可得

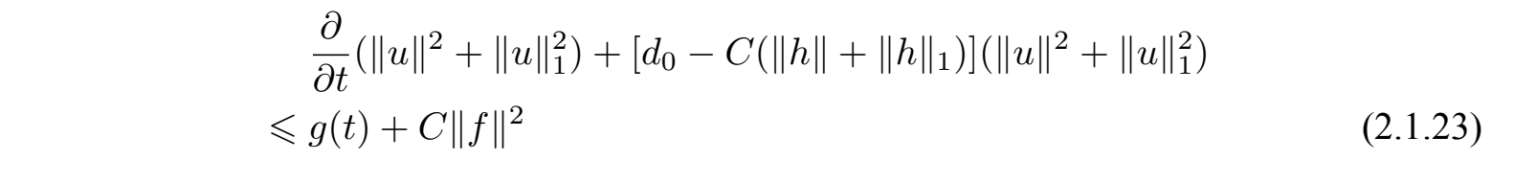
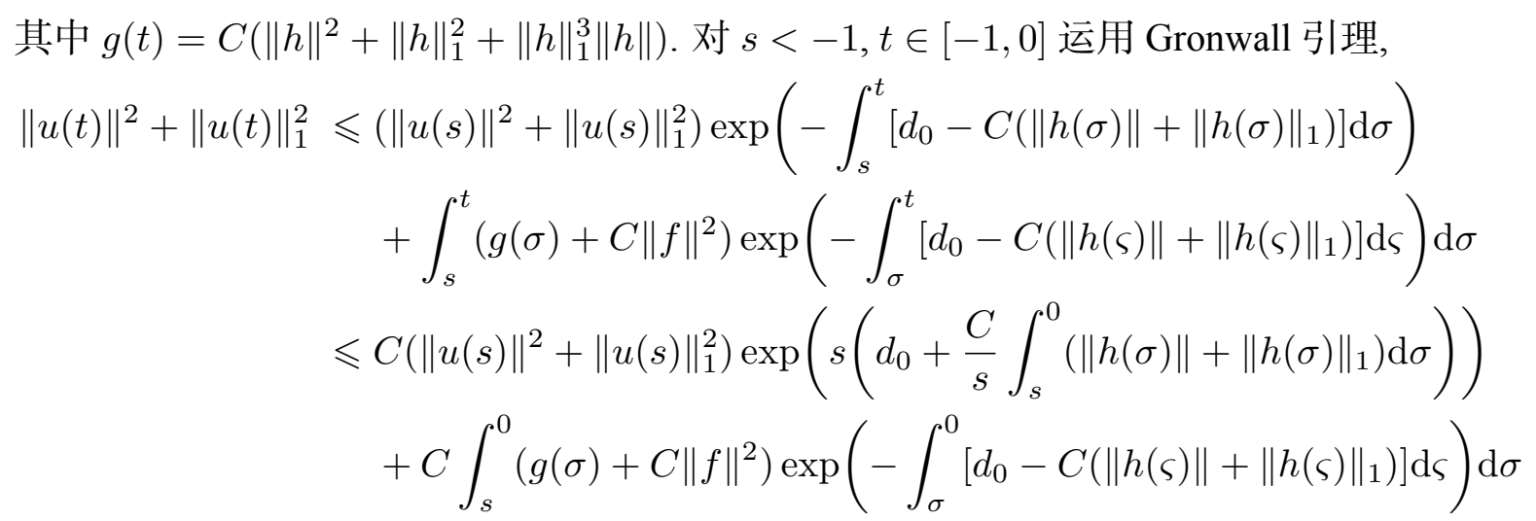
因为h(t)是取值于D(A) ⊂ 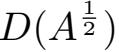⊂ H的遍历过程，当s→−∞时，我们有

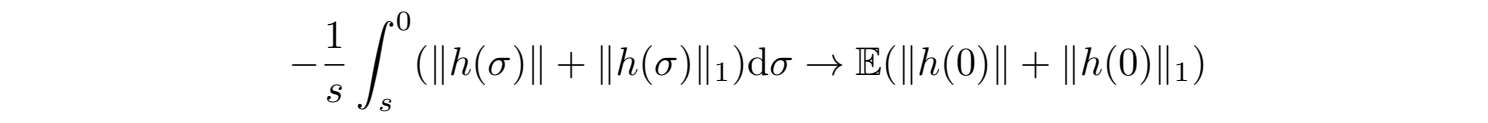
于是存在s ₀ (w)，使得当s < s ₀ (w)时，

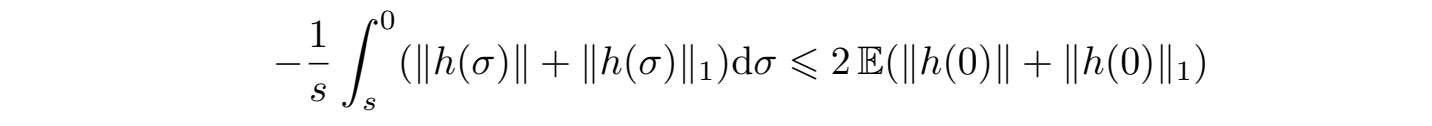
并且当τ足够大时，

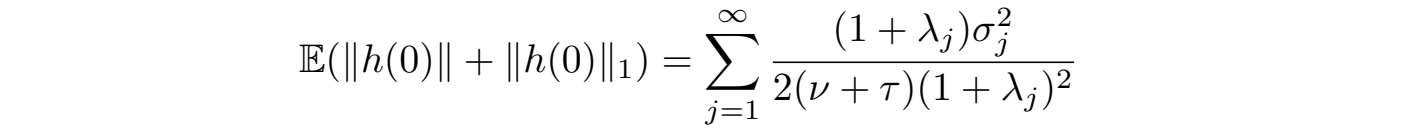
可以任意小，因此

类似文献[88]，我们有g(s)至多按多项式增长，又g(t)与指数衰减的函数相乘，由此可知上式积分存在.我们得到存在依赖B和w的时刻s ₁ (w，B)，满足当s < s ₁ (w，B)，t∈[−1，0]时，下式成立.

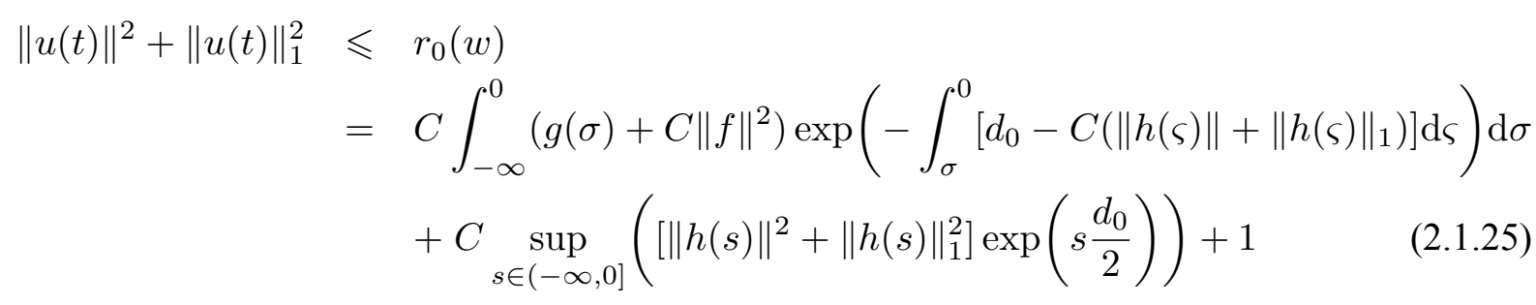
记K(w)是V中半径为 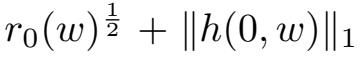的球，我们得到对V中任意有界集B，存在 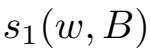，满足当s < 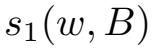时，

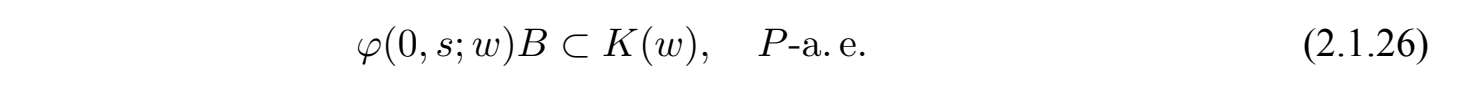
这就意味着在0时刻存在吸收集K(w).为了得到全局随机吸引子，需要对紧性进行研究.

我们有下面渐近紧的一些结论.

定理2.1.2 ^{[8，11，89]} 若半群S(t)：V→V能被分解成

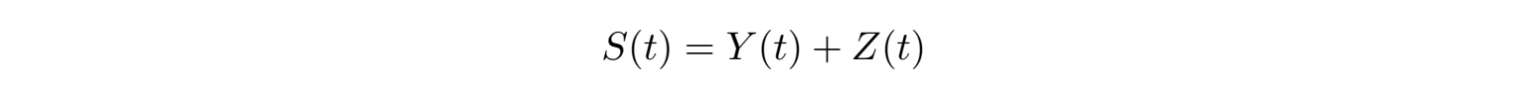
其中Z(t)是V中的紧算子，若存在连续函数k： × 满足R>0，当t→∞时，k(t，R)→0且有

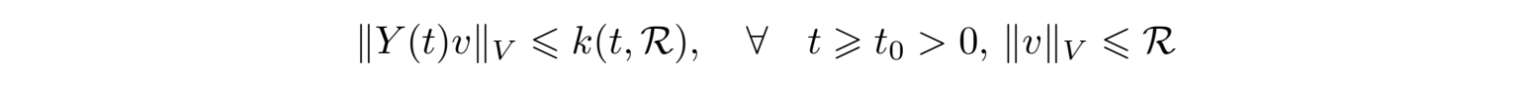
成立，则有S(t)：V→V，t⩾0是渐近紧的.

定理2.1.3 方程(2.1.11)生成的半群S(t)在空间V中渐近紧.

证明 ：令 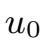∈V .我们首先将S(t)分解成 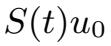= 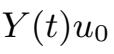+ 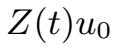，其中Y (t)是由以下方程生成的半群

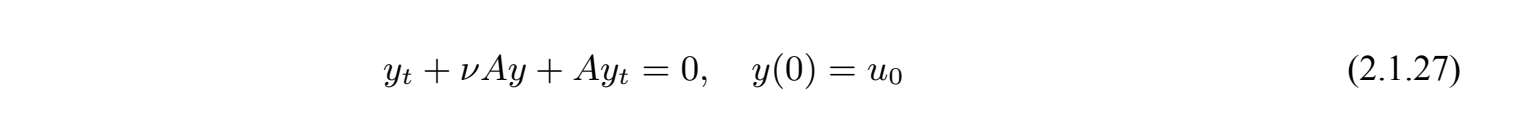
然后有z(t)= 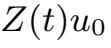是以下方程的解

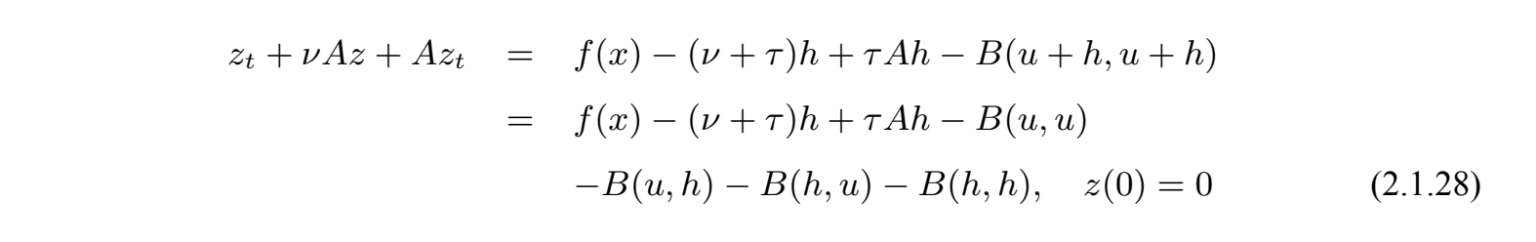
其中u方程(2.1.11)具有初值u ₀ 的解.

对方程(2.1.27)两边关于y做内积，由文献[44]可得半群Y (t)：V→V是指数压缩的.

由Hölder不等式和Sobolev不等式，有 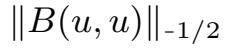⩽ 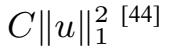和 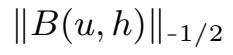⩽ ⩽ 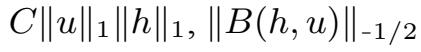⩽ 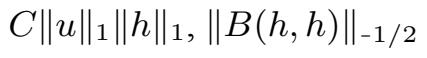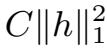.这里我们仅验证 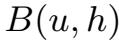，其他类似.

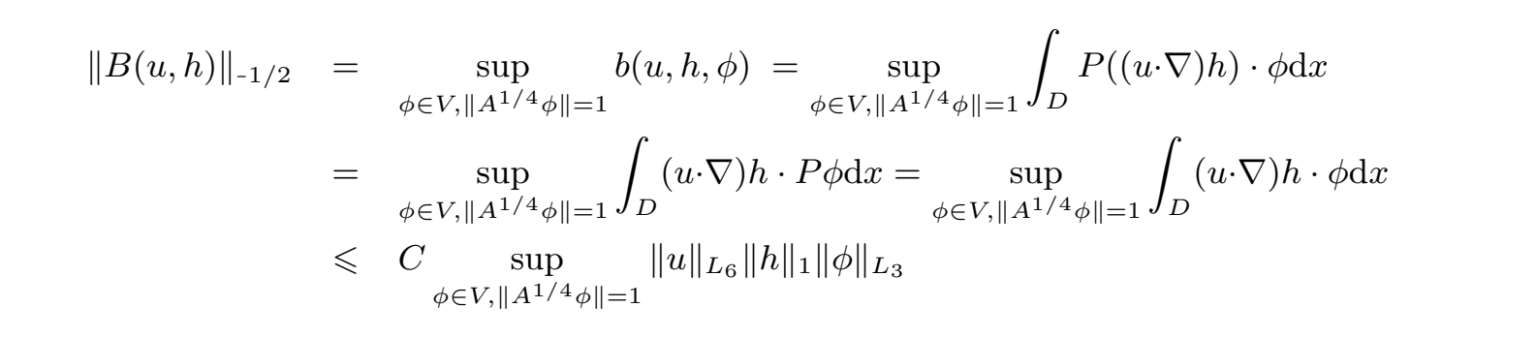
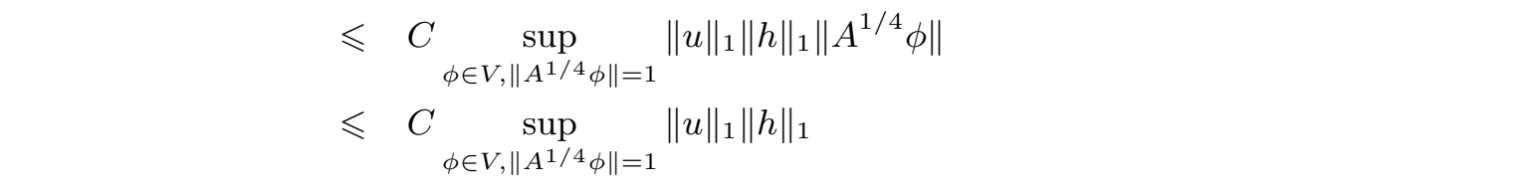
由上述不等式和文献[44]的命题3.1 可知，(2.1.27)的解属于 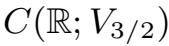，这意味着算子Z(t)映V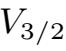入 .又因嵌入 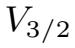⊂ V是紧嵌入，由定理2.1.2 可知S(t)是渐近紧的.

定理2.1.4 三维随机Navier-Stokes-Voight方程(2.1.1)～(2.1.3)具有全局随机吸引子.

证明 ：因h(t)是D(A) ⊂ V值的，由嵌入定理和定理2.1.3 可得随机流φ对P-a. e. w在V中是渐近紧的.由定理1.1.2 我们得到存在全局随机吸引子A(ω)，其吸收任意一个非随机有界集B ⊂ V .

注 2.2： 若进一步假设v0∈D(A)，对方程(2.1.11)两边关于Au(t)做内积，我们也将得到在 空间V ₂ 中存在随机全局吸引子. jCZtbRlxFqknPZKiwpgk5mUWGtZMFbxNdcGPs3znCsjEmGVc20HrVfQ9RU9fu+Rw