




由上一节内容可知,若f(x)在开区间(a,b)上连续,在左端点a处右连续,右端点b处左连续,则称f(x)为闭区间[a,b]上的连续函数.闭区间上的连续函数有很多性质往往是开区间上连续函数所不具备的,这些性质无论在理论研究方面还是实际应用中都有很高的价值,其中不少性质从几何上直观地看是很明显的,但证明却不容易,需要用到实数理论,我们将以定理的形式把这些定理叙述出来,但略去严格的证明.
定义1-19 对于区间I上有定义的函数f(x),如果有x 0 ∈I,使得x∈I,有
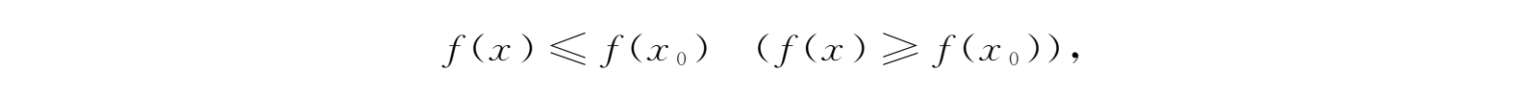
则称f(x 0 )是f(x)在区间I上的最大值(最小值).
例如,f(x)=arcsinx在[-1,1]上有最大值
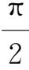 ,最小值
,最小值
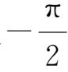 ,在(0,1]上有最大值
,在(0,1]上有最大值
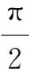 ,没有最小值,在(-1,1)上没有最大值和最小值.
,没有最小值,在(-1,1)上没有最大值和最小值.
若函数f(x)在区间I上有最大值和最小值,则f(x)在区间I上有界,反之不成立.
定理1-14(有界性与最大最小值定理) 在闭区间上连续的函数在该区间上有界且一定能取得它的最大值和最小值.
(1)开区间结论不一定成立,如f(x)=sinx,x∈
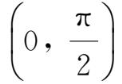 ,见图1-29.
,见图1-29.
(2)区间内有间断点结论不一定成立,见图1-30.
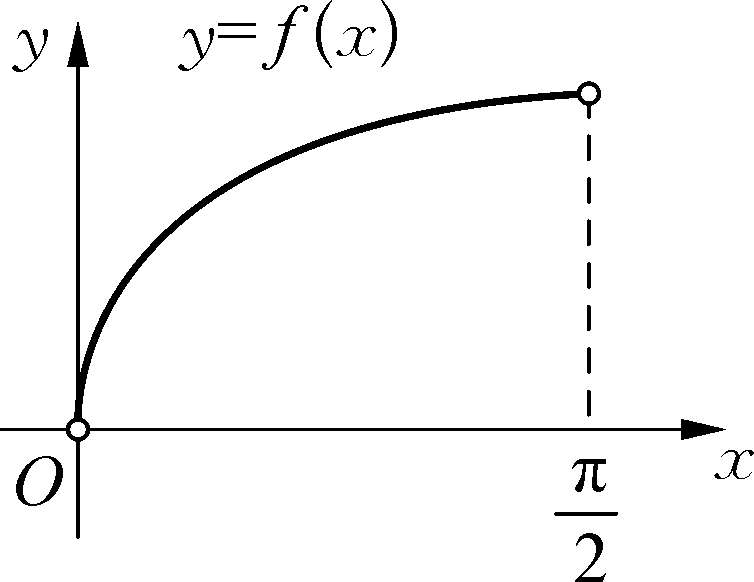
图1-29
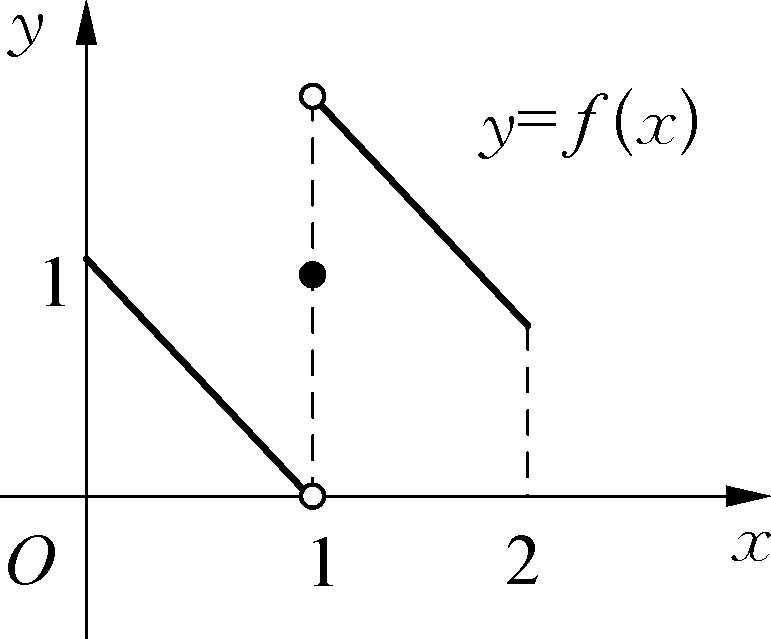
图1-30
定义1-20 若x 0 使f(x 0 )=0,则x 0 称为f(x)的零点.
定理1-15(零点定理) 设函数f(x)在闭区间[a,b]上连续,且f(a)f(b)<0(即f(a)与f(b)异号),那么在开区间(a,b)内至少有一点ξ使f(ξ)=0(如图1-31).
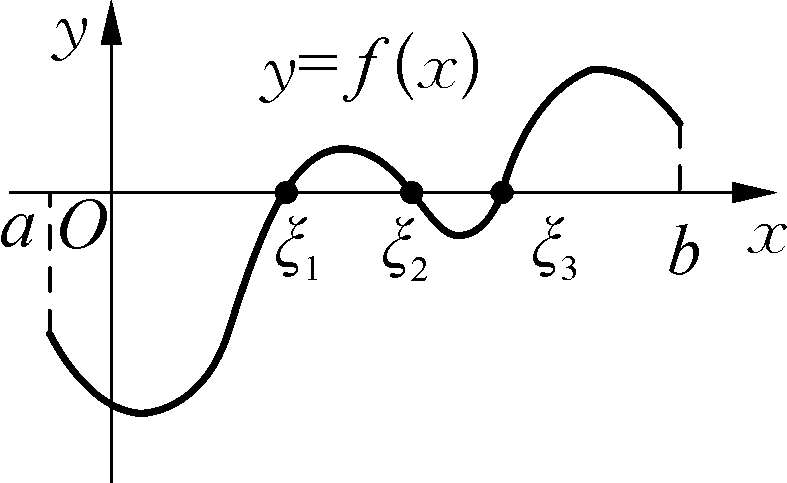
图1-31
若将条件f(a)f(b)<0改为f(a)f(b)≤0,则结论中(a,b)改为[a,b].
【例1-7-1】
证明方程sinx+x+1=0,在
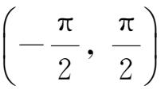 内至少有一个根.
内至少有一个根.
证明
令y=f(x)=sinx+x+1,则f(x)在
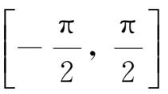 上连续,
上连续,
且
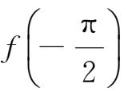 =
=
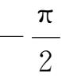
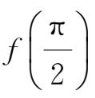 =
=
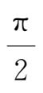 +2>0,由零点定理至少存在ξ∈
+2>0,由零点定理至少存在ξ∈
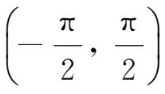 ,使得f(ξ)=0,即方程至少有一个根.
,使得f(ξ)=0,即方程至少有一个根.
【例1-7-2】 证明方程x2 x =1至少有一个小于1 的正根.
证明 令f(x)=x2 x -1,则f(x)在[0,1]上连续,且
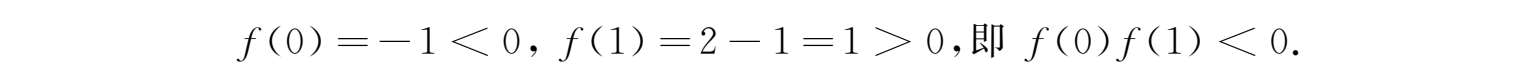
由零点定理ξ∈(0,1),使得f(ξ)=0,即x2 x =1至少有一个小于1 的正根.
【例1-7-3】 设函数f(x)在区间[a,b]上连续,且f(a)<a,f(b)>b,证明存在ξ∈(a,b),使得f(ξ)=ξ.
证明 令F(x)=f(x)-x,则F(x)在[a,b]上连续,且
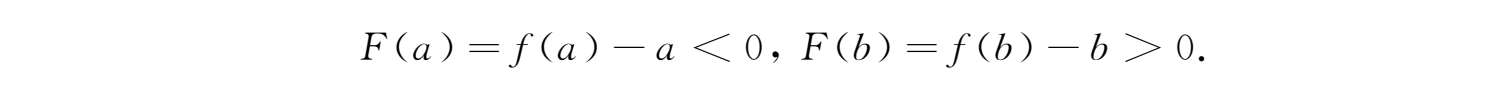
由零点定理存在ξ∈(a,b),使F(ξ)=0,即f(ξ)=ξ.
【例1-7-4】 设f(x),g(x)在[a,b]上连续,f(a)<g(a),f(b)>g(b),证明存在ξ∈(a,b),使
f(ξ)=g(ξ).
证明 令F(x)=f(x)-g(x),x∈[a,b],则F(x)在[a,b]上连续,
F(a)=f(a)-g(a)<0,F(b)=f(b)-g(b)>0.
由零点定理存在ξ∈(a,b)使F(ξ)=0,即 f(ξ)=g(ξ).
定理1-16(介值定理) 设函数f(x)在闭区间[a,b]上连续,f(a)=A及f(b)=B,且A≠B,则对于介于A与B之间的任意一个数C,在开区间(a,b)内至少有一点ξ,使得
f(ξ)=C (a<ξ<b).
证明 设φ(x)=f(x)-C,则φ(x)在闭区间[a,b]上连续,且φ(a)=A-C与φ(b)=B-C异号.
根据零点定理,开区间(a,b)内至少有一点ξ,使得φ(ξ)=f(ξ)-C=0 (a<ξ<b),即
f(ξ)=C (a<ξ<b).
推论1-6 设f(x)在闭区间[a,b]上连续,则f(x)在闭区间[a,b]能取得介于最大、最小值之间的任何值(如图1-32).
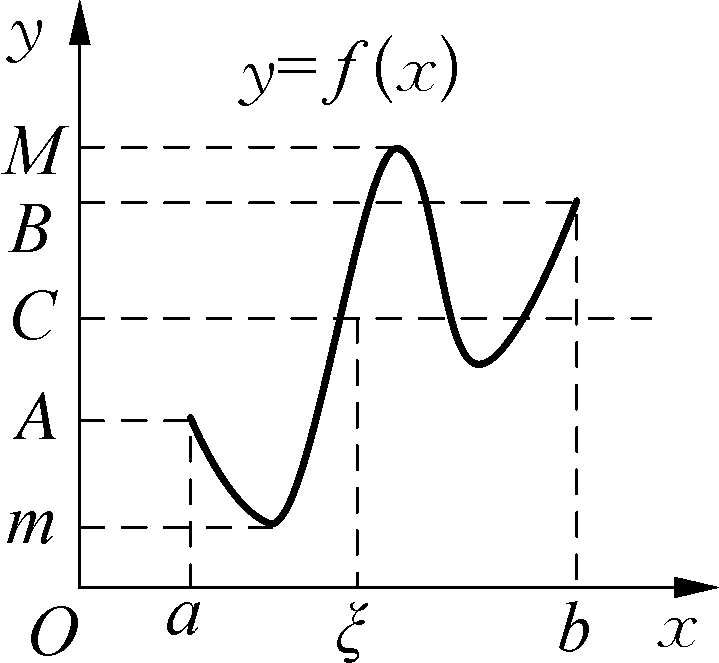
图1-32
【例1-7-5】
设f(x)在闭区间[a,b]上连续,证明∃ξ∈[a,b],使得f(ξ)=
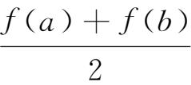 .
.
证明 不妨设f(a)≤f(b),则
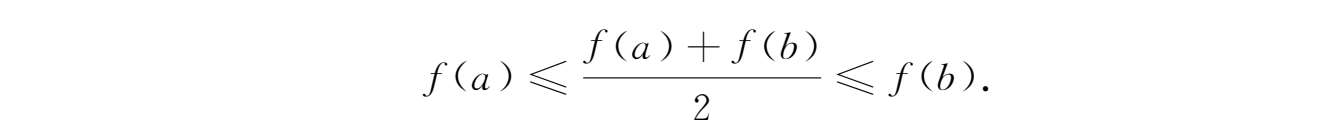
由介值定理存在ξ∈[a,b],使得f(ξ)=
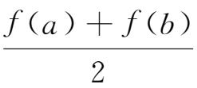 .
.