




由折射定律可知,光路传输需要准确计算光线入射角度的正弦值。一阶近似只适用于近轴光学,本质上是理想光学,因此是没有像差的。如果采用三阶近似,就可以推导出光学系统的像差,对应的这种像差,也被称为初级像差或三阶像差:

因为最早的这些计算公式是由赛德尔(Seidel)推导出来的,所以这些三阶像差也被称为赛德尔像差。赛德尔像差包含5个三阶像差和2个一阶(轴向和垂轴)色差。这些理论有助于进一步理解如何降低或消除几何像差,对于理解光学设计非常重要。赛德尔像差系数按照如下方式进行计算:

通过光线追迹的实现,几何光学可以用不同的形式来进行计算,传统的几何像差最初是以初级像差为主,包括五个单色像差和两个色差,通常以赛德尔像差系数(图2-3)来进行评价。轴外部分则需要以真实光线追迹为基础,以不同形式展现。本质上,赛德尔像差的计算通过追迹近轴光线的主光线和边缘光线,从而获得光线角度和高度就可以完成计算。
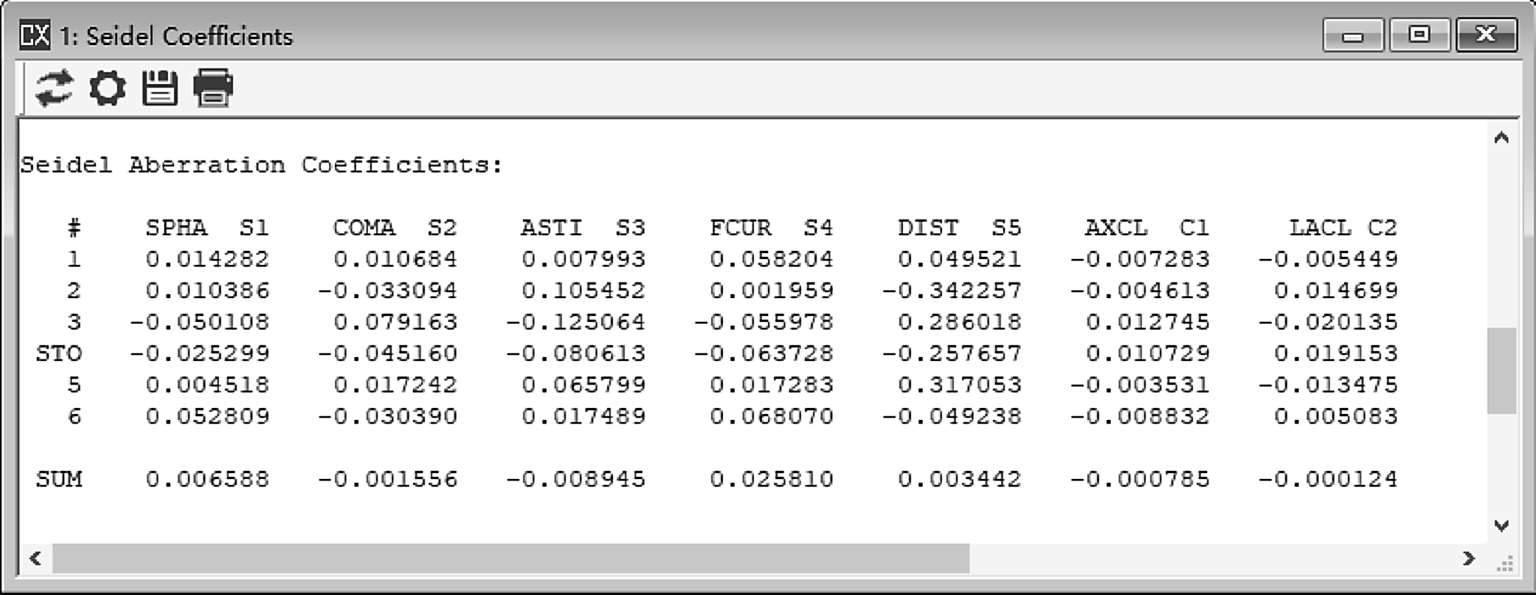
图2-3
以上是光学设计中最常用的像差分析方法,基于近轴光线,所以也是最基本的,这些像差通常适用在分析近轴光学的系统上。
接下来讨论一下5个三阶的赛德尔像差:
将光学系统的波前用赛德尔多项式表示:
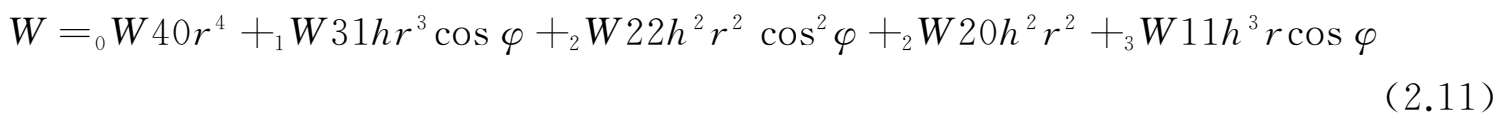
其中r和φ表示光瞳面上的极坐标位置,h表示像高。

由以上公式可知三阶球差和光瞳高度的四次方r 4 成正比,在单色光的情况下,近轴视场就可以产生。
用一个单透镜作为实例(图2-4),这个透镜只有三阶球差,球差玻前和光线扇形图如图2-5,图2-6所示。
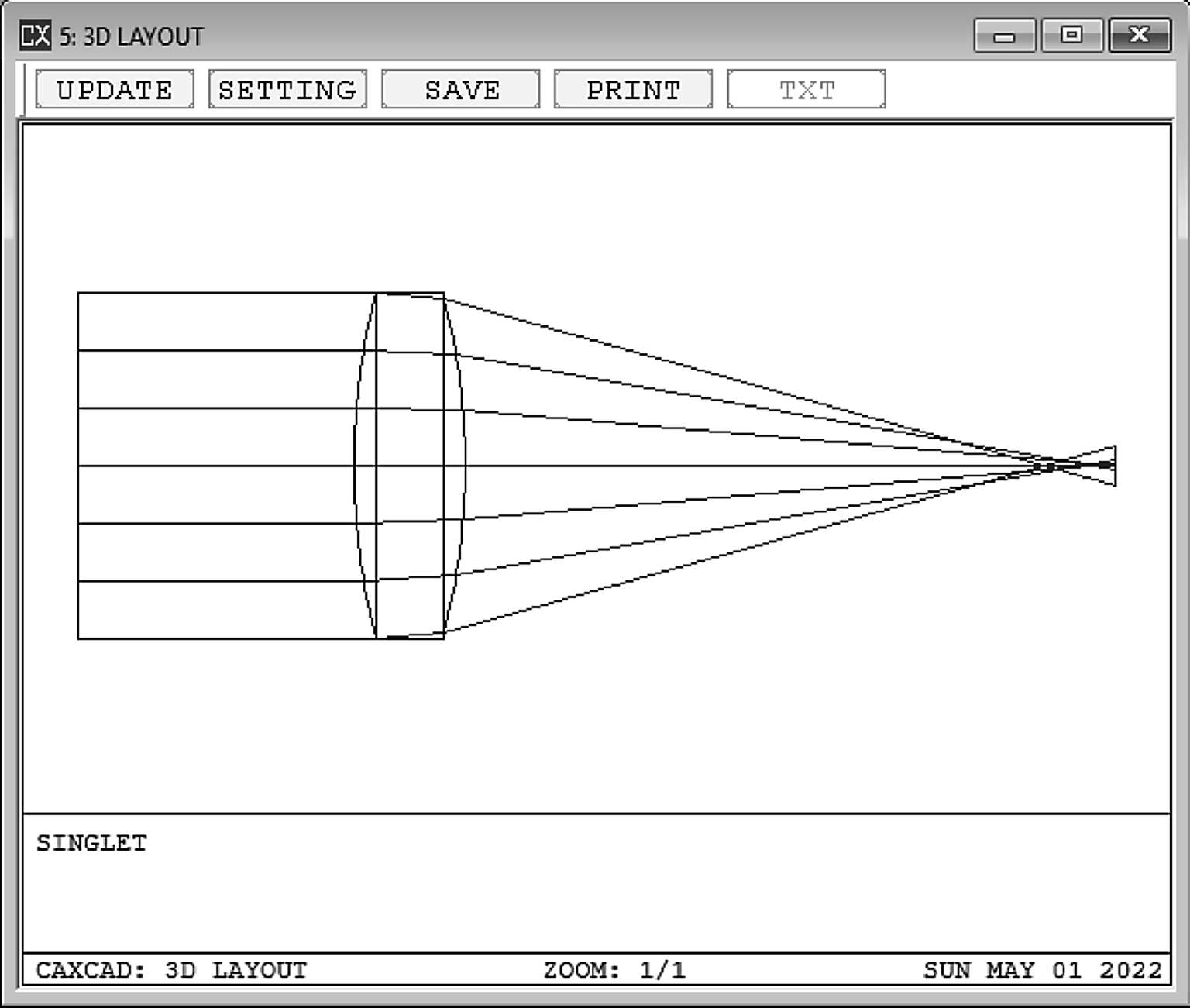
图2-4
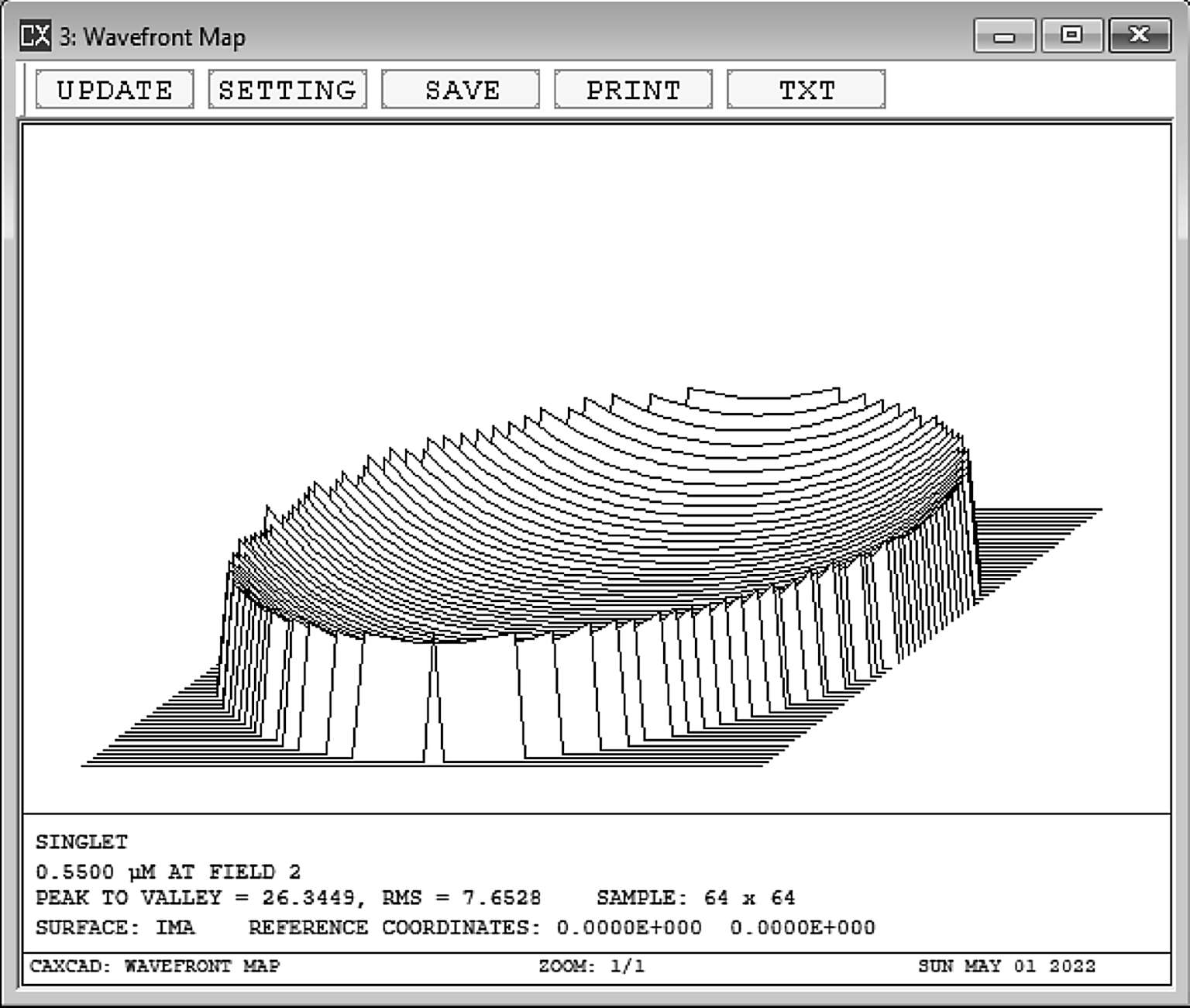
图2-5
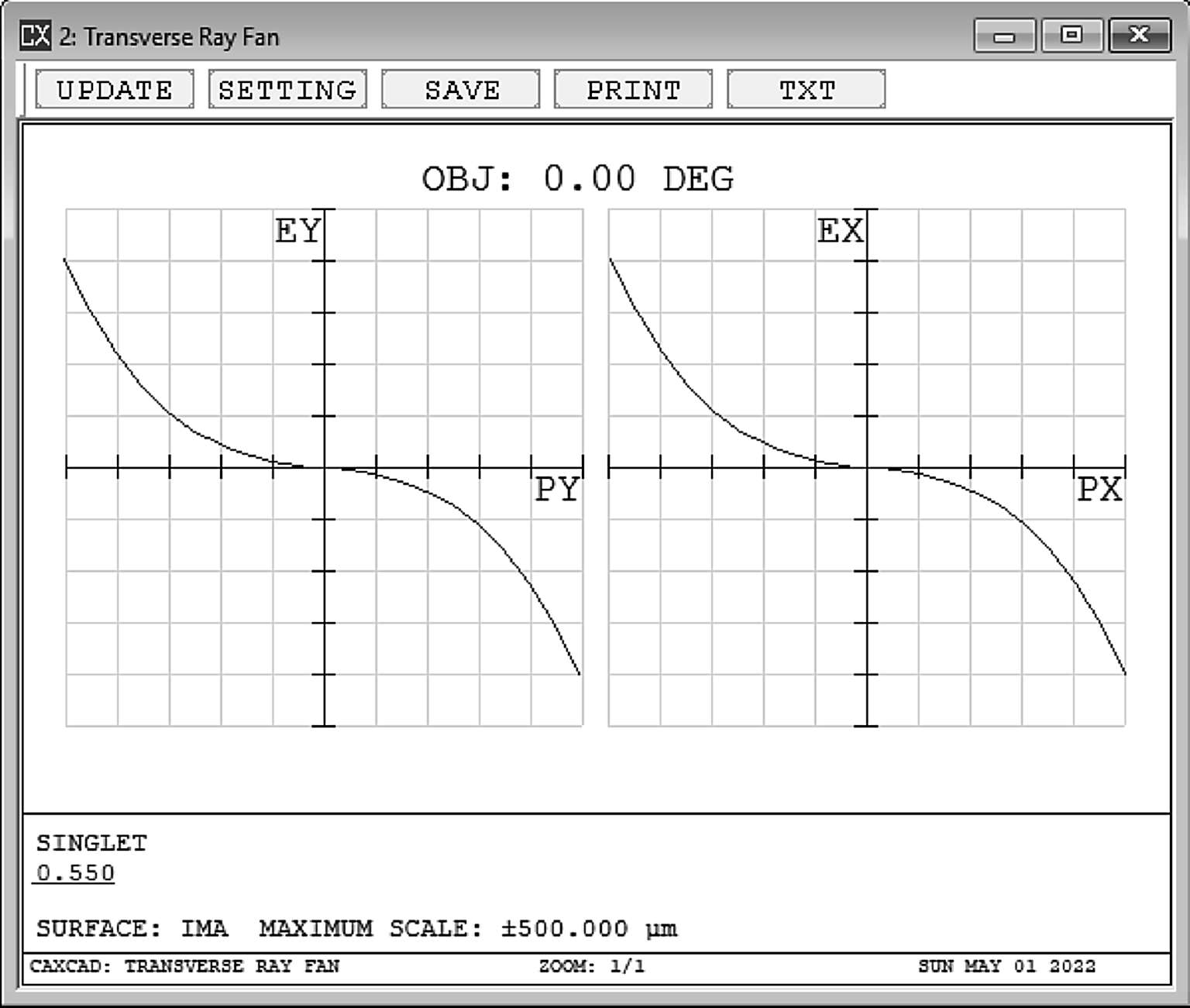
图2-6
这是对球差最容易理解的形式,从左侧来自不同孔径高度的光线在轴上的焦点不同(图2-7),因此在像面上就无法获得完美汇聚的光斑(图2-8)。而且我们也可以看到,这样的镜头,最佳光斑的位置并不会是近轴焦点位置。
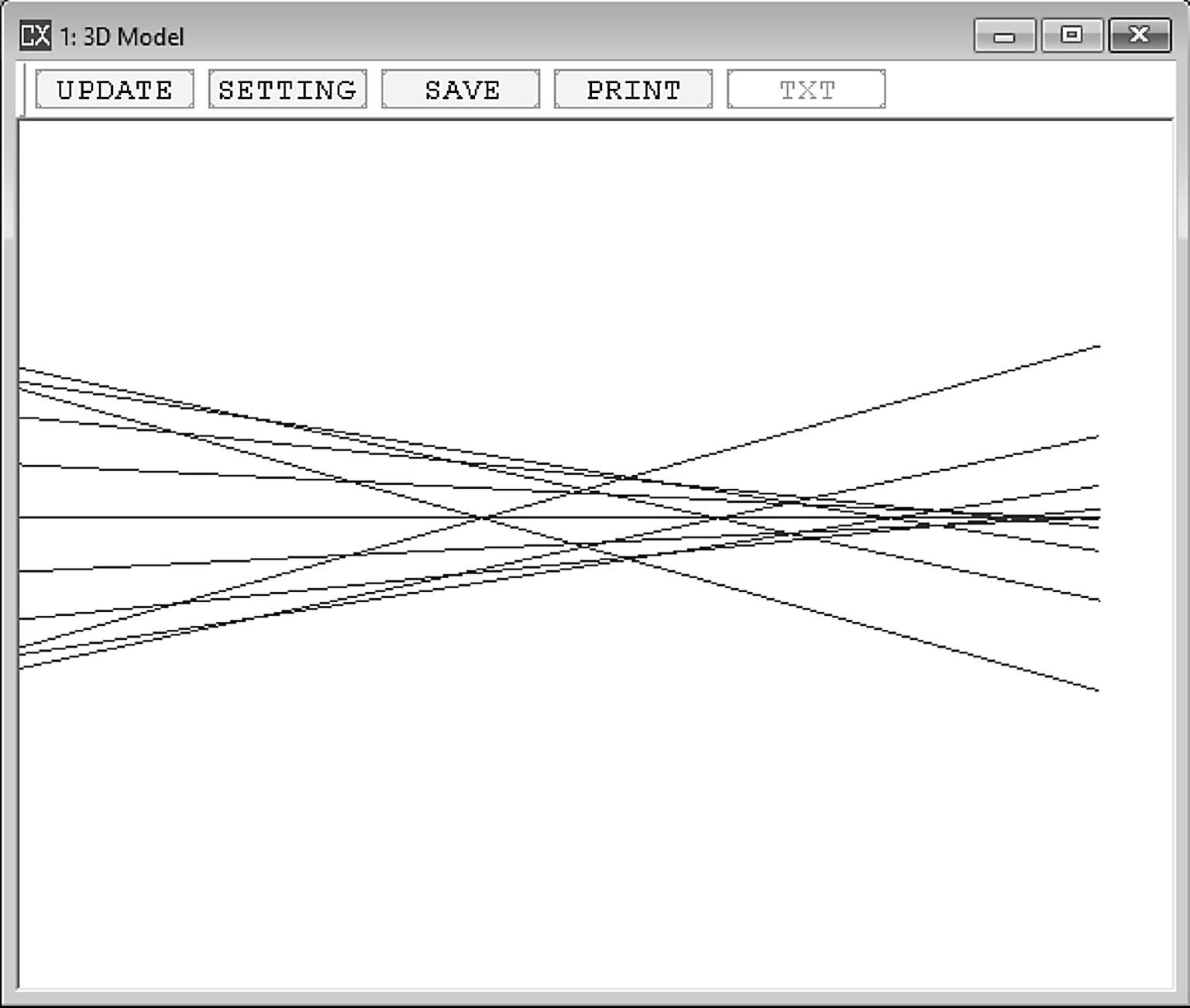
图2-7
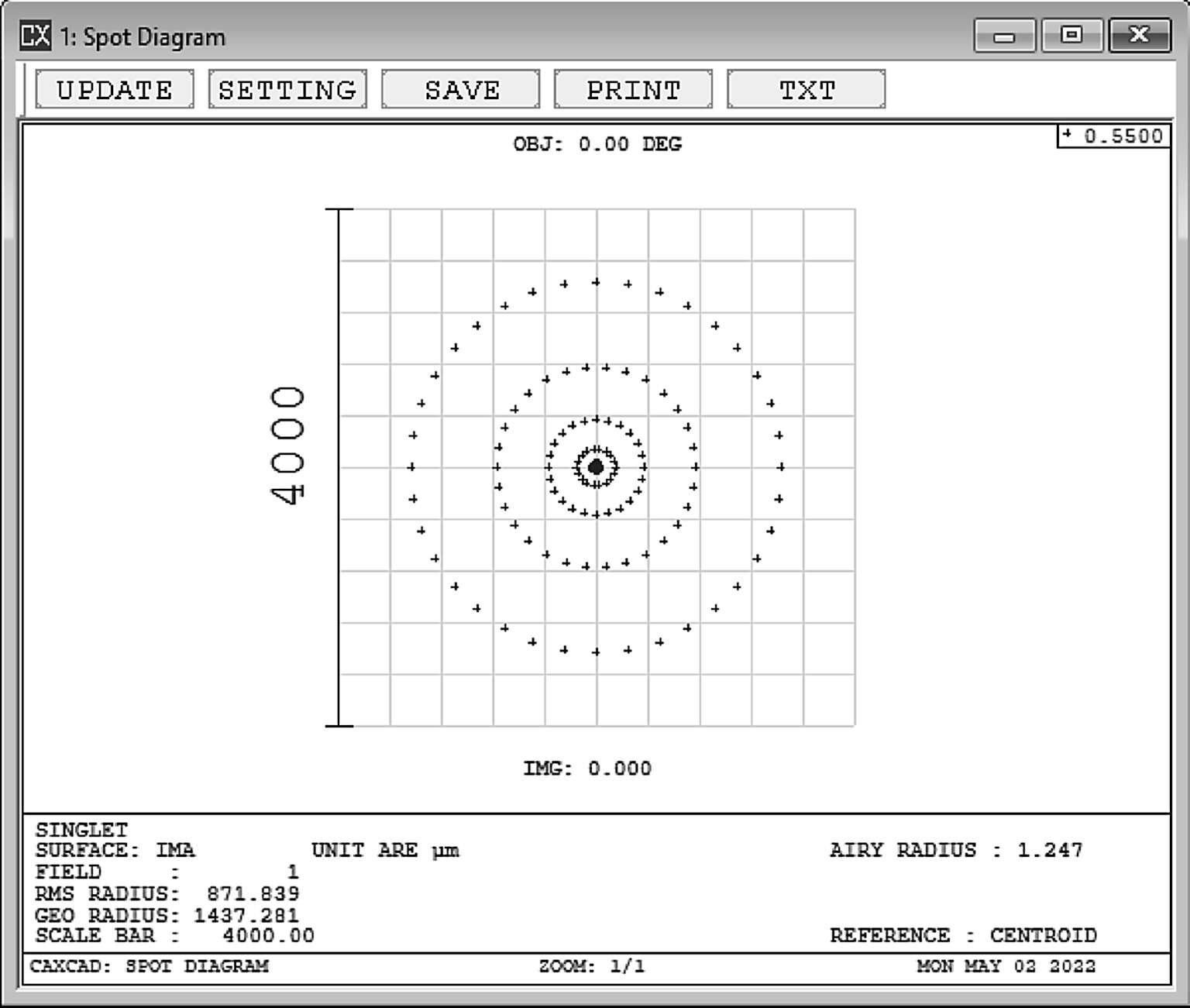
图2-8

相对于中心视场典型的球差,光斑是旋转对称的,而彗差则不同。从上面的公式能够看出有一个y项,所以对于y=0的时候,或者说特定情况下对于子午或弧矢方向(子午和弧矢分别代表垂直和水平方向)彗差会是0。
利用泽尼克多项式面型和理想透镜,可以快速构建一个典型的,具有彗差的系统,如图2-9所示。
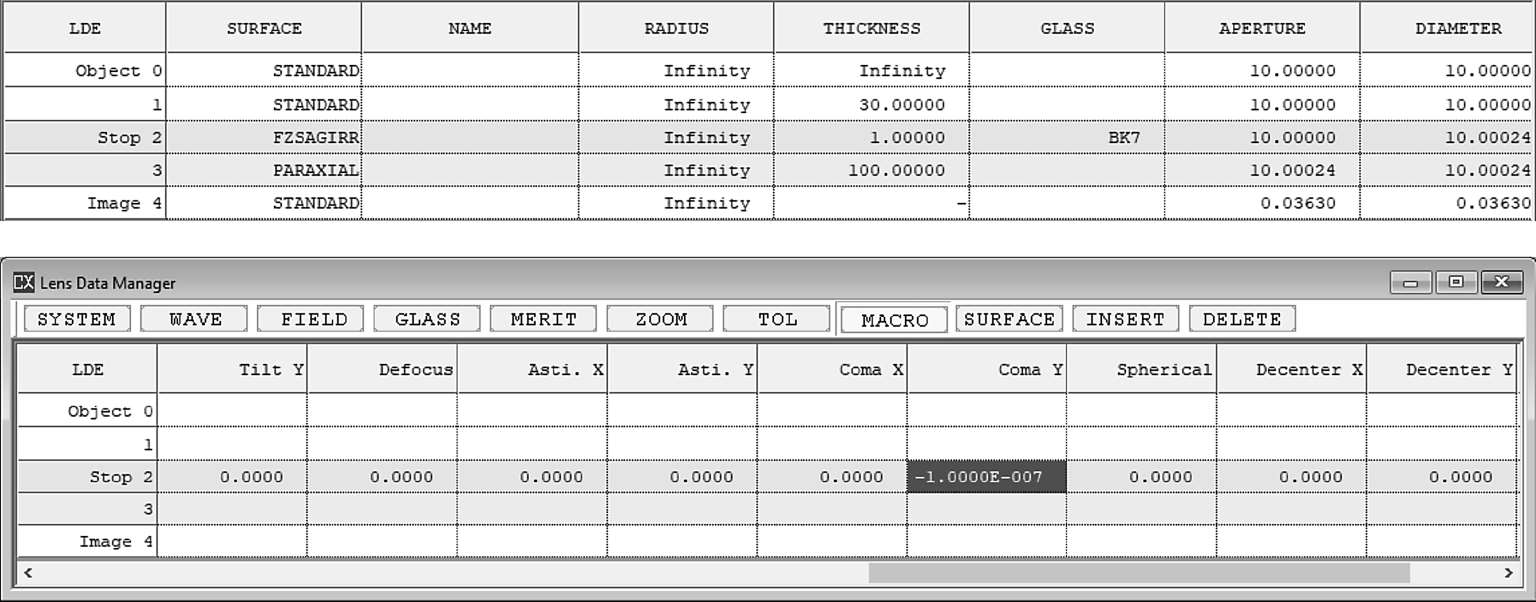
图2-9
彗差的本质是当一束光以倾斜的角度进入光学系统后,来自不同环形区域的光线,放大率不同。同时在倾斜的方向,不同放大率的光线中心都发生了偏移,这样就使光斑形成了一种典型的彗星形状,这是彗差名称的由来。图2-10展示了典型的彗差点列图。从中可以看到,彗差光斑是由很多直径不同的环形光线偏移组合在一起的。
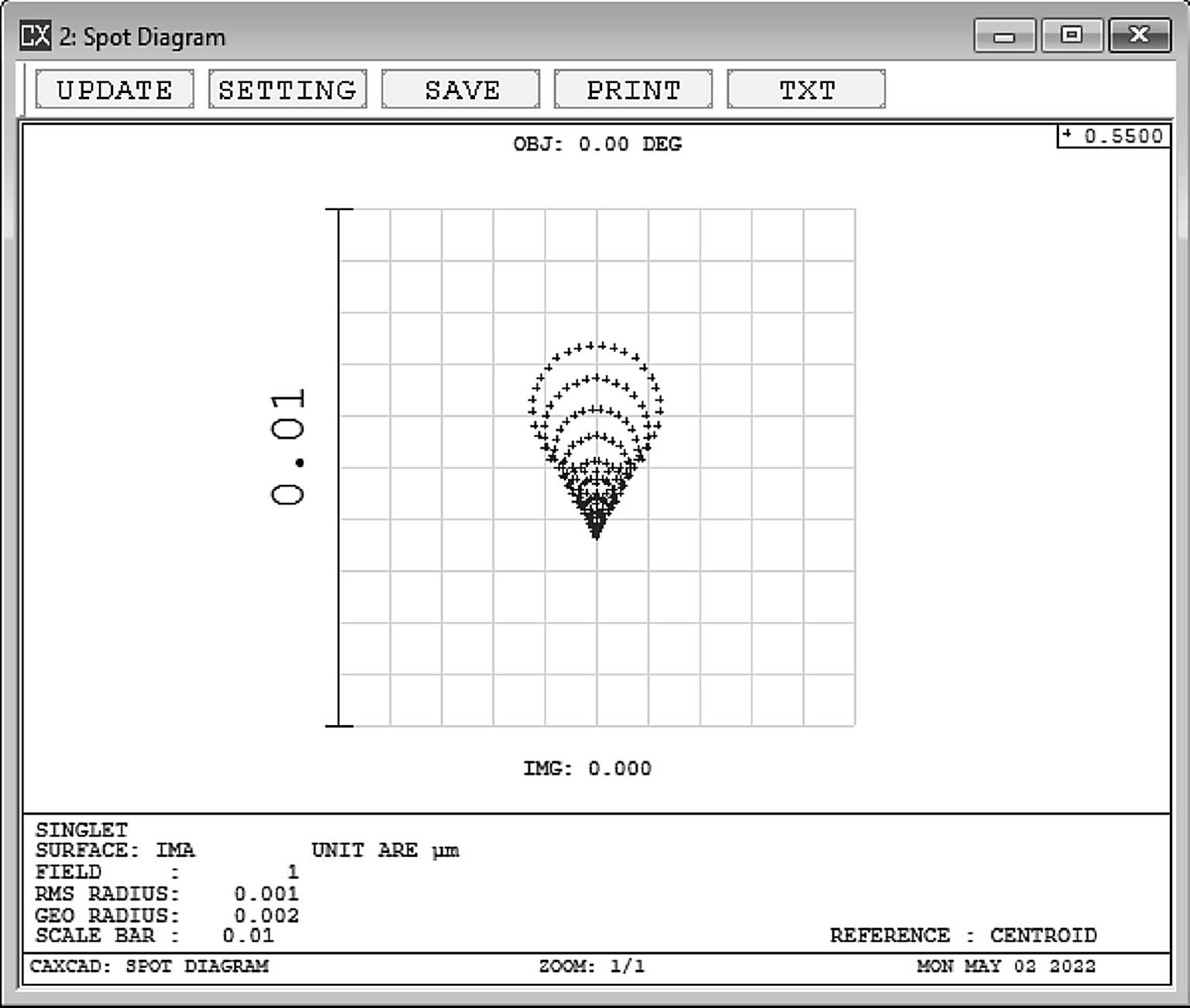
图2-10
图2-11是彗差的光线扇形图:可以看到,子午方向左右对称,弧矢方向数值为0。
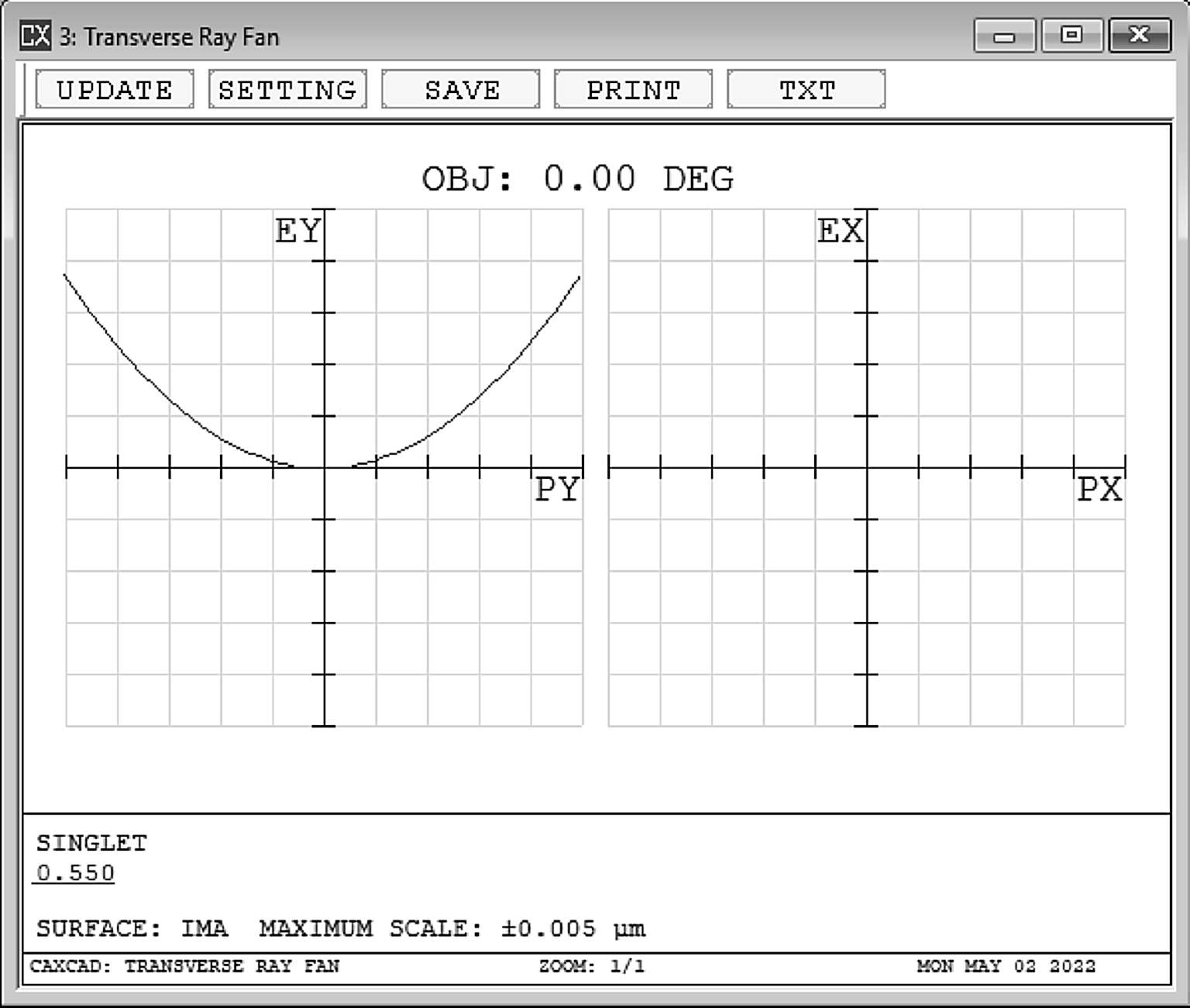
图2-11
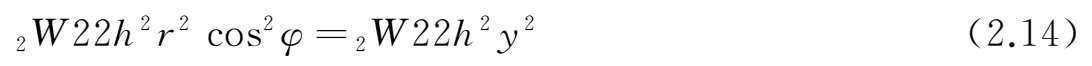
像散的本质是镜头水平方向和垂直方向的焦距或焦点不同,因此主要是光斑在子午方向和弧矢方向的差异。接下来尝试利用一个柱面镜来构建轴上光线的像散作为实例。提到柱面镜和像散就会想到人眼的散光,它表示人眼水平方向和垂直方向的焦距不一致,所以利用柱面镜来消除散光也是矫正像散的方法。
如图2-12所示为利用CYLINDER柱面镜构建像散的初始表面数据。
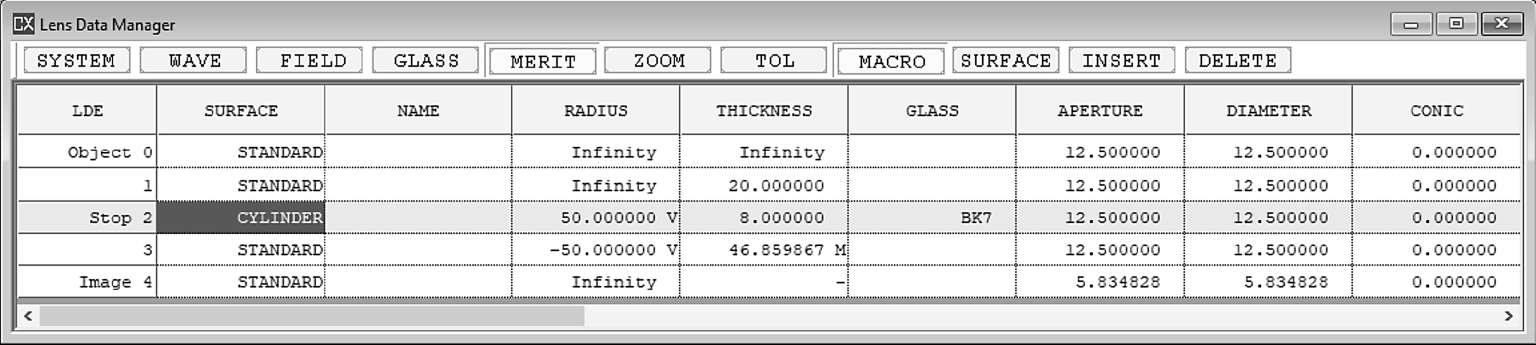
图2-12
如图2-13所示,中心光斑在水平和垂直两个方向存在明显的差别,这是因为这个系统在这两个方向焦距也不一样。
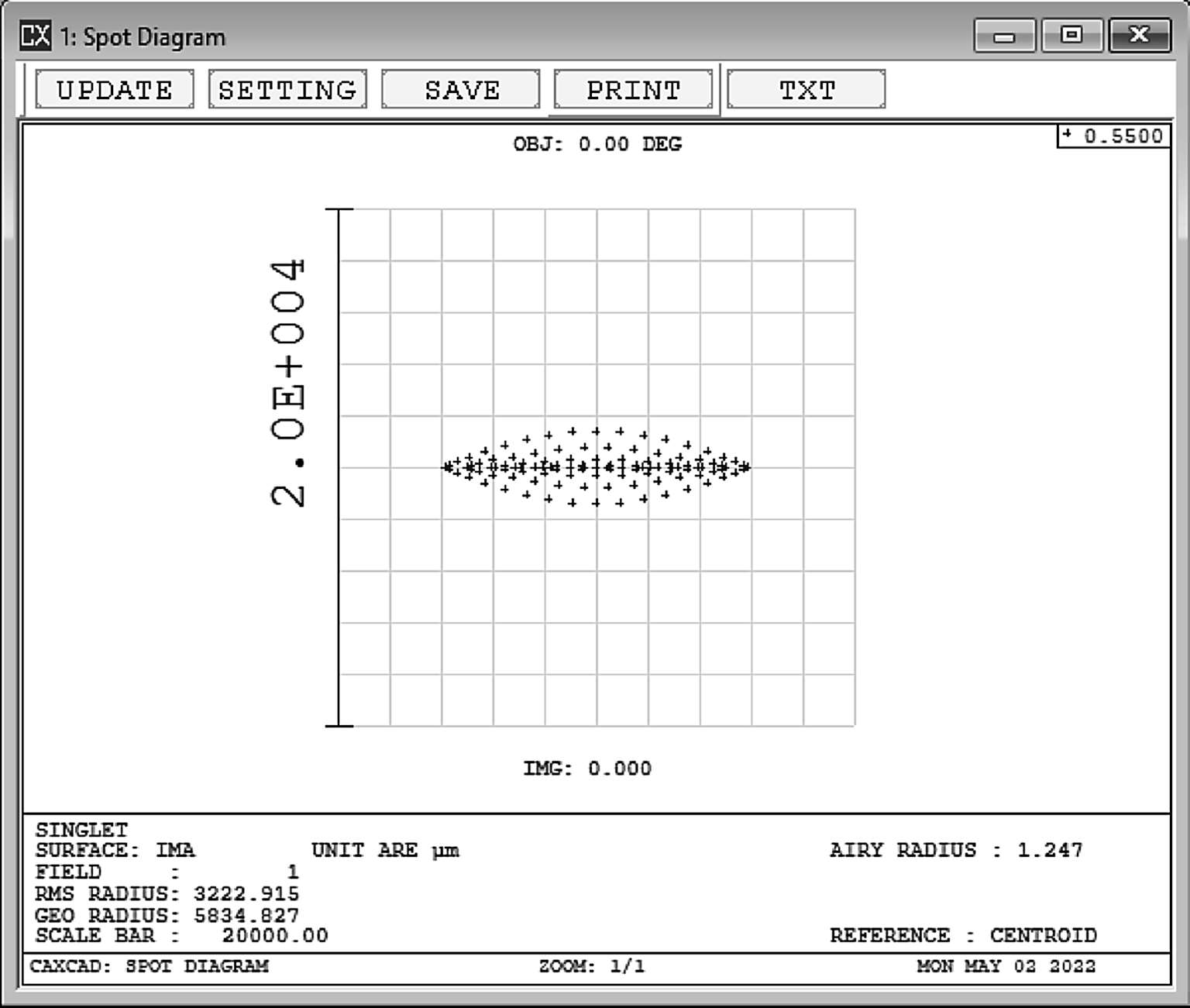
图2-13
如图2-14所示,利用优化操作数EFLX、EFLY来查看和控制x和y方向的焦距。同时这两个操作数还有另外一个功能,就是它们提供了面型的范围设置,可以用来控制指定面形范围或者镜头组的焦距:

图2-14
对于柱面的扩展:可以利用TOROIDAL环形或者轮胎面型,除了在y方向可以指定曲率半径,在x方向也可以定义高次的非球面,因此这个面型就相当于柱面的扩展。
优化控制光斑的像散有很多种,可以使用ASTI,同时也可以使用真实光线追迹,例如针对某一个视场利用REAY、REAX分别抓取光斑的上下和左右光瞳边缘的两根光线,让它们的差值朝着相同的目标进行优化,就可以控制x和y两个方向消除像散。在新版的CAXCAD中直接可以使用ASXY进行像散控制。
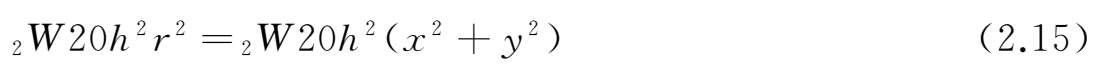
场曲,顾名思义就是视场发生了弯曲,指的是像面的最佳焦点不在一个平面上(平场),而是在一个曲面上。视场越大,场曲的数值也越大,通常倾斜角度的光线到达像面需要传播更长的距离,所以光线就会提前聚焦,如图2-15~图2-16所示:

图2-15
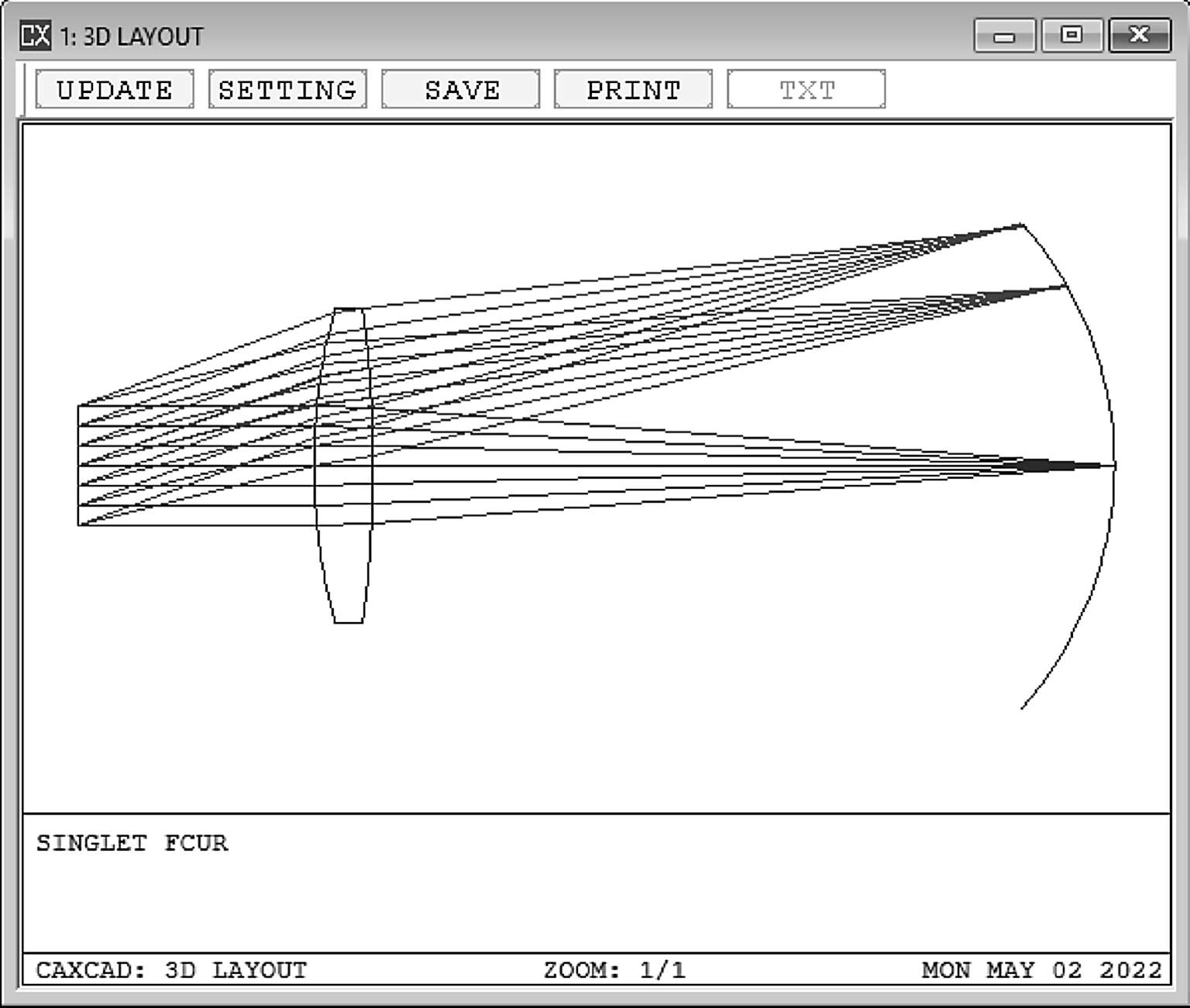
图2-16
控制场曲的方法有两种:
(1)在系统中引入场镜,让其对大视场的光线贡献更多的负焦距,这个场镜通常是一个平凹透镜,如图2-17的镜头是1840年匈牙利数学家、物理学家约瑟夫·佩茨瓦尔(Joseph Petzval)发明的两组双胶合Petzval透镜,其中最后一片凹面镜就是可以很好地矫正场曲的场镜。
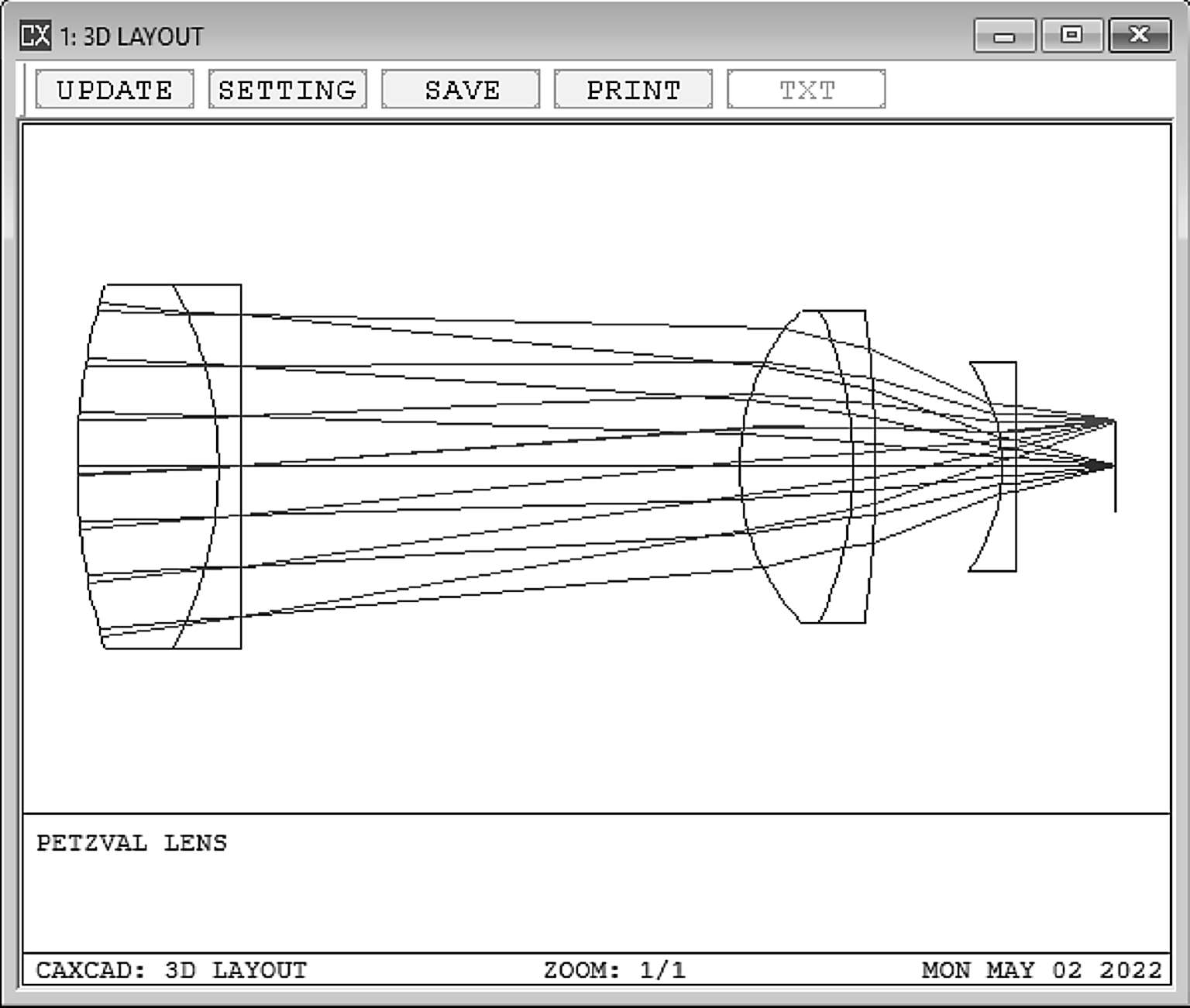
图2-17
提到场曲这种像差,就需要提及天文望远镜。因为很多典型的反射式天文望远镜都是采用场镜来矫正场曲的。例如马可苏托夫望远镜(图2-18):
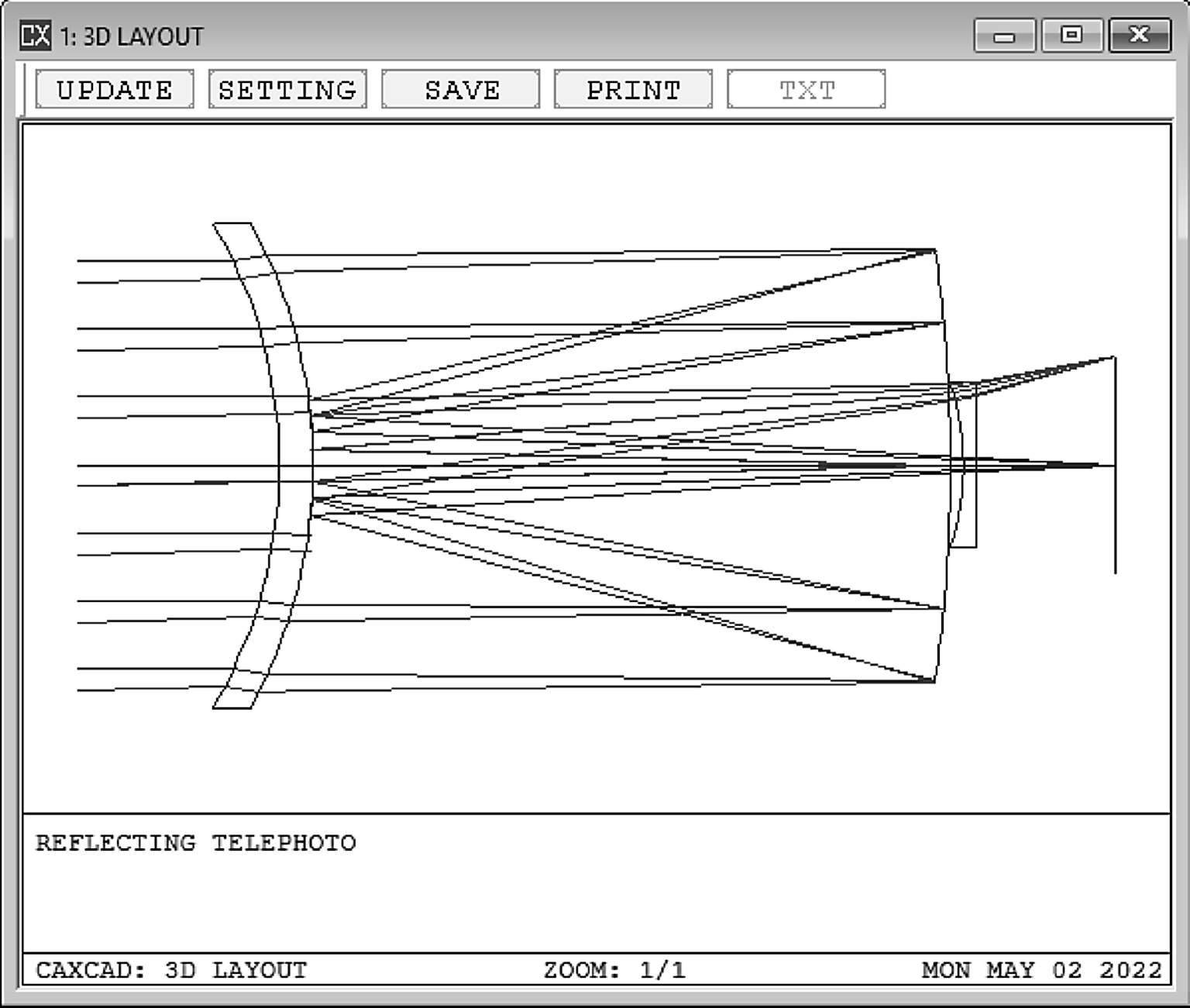
图2-18
折反射望远镜有一个非常大的好处就是可以做到没有色差。利用非球面的面型可以将球差校正的很小,小视场的系统,彗差和像散也不大。但是场曲如果引入一个玻璃材料的场镜,就会存在两个问题,第一个是玻璃材料会引入色差,第二个是紫外或者红外波段的透过率会受到影响。基于这些因素,哈勃望远镜直接用了一个曲面的探测器作为像面(图2-19)。
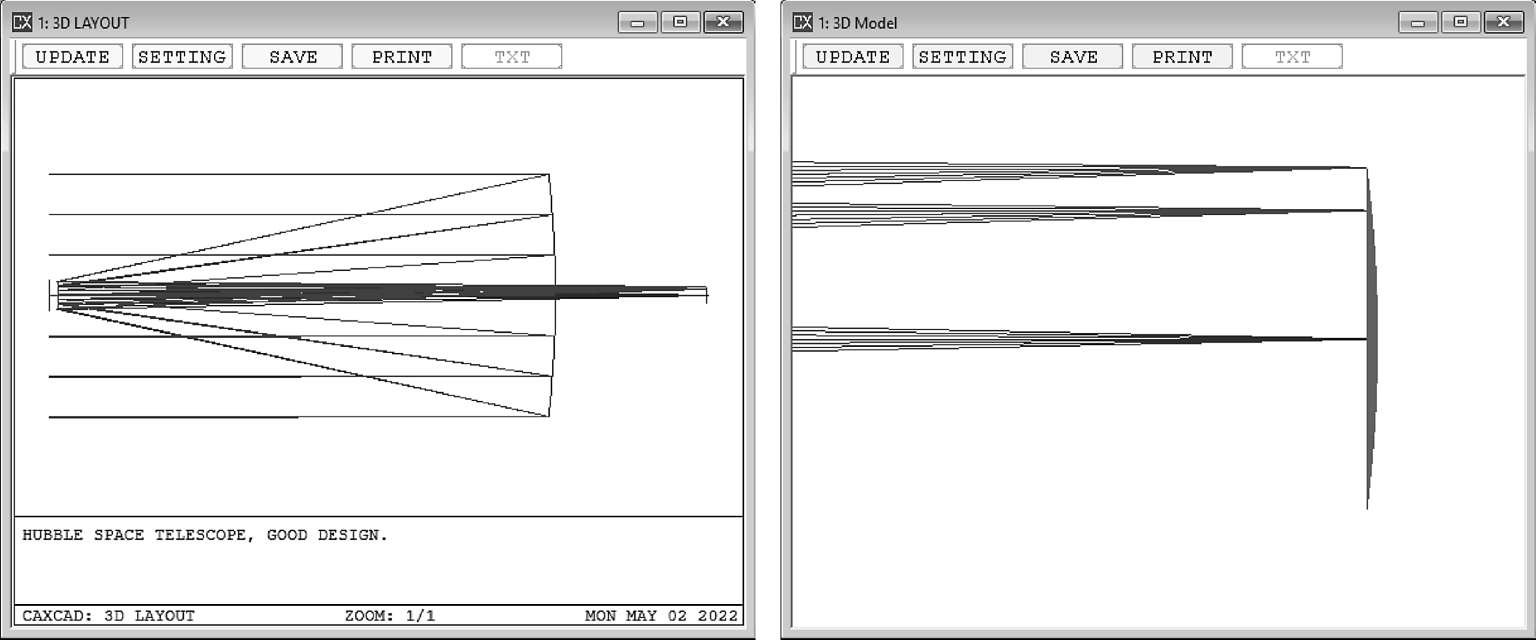
图2-19
对于没有像差的理想光学系统来说,所有的光线都满足F-Theta条件,即像高是焦距和入射角度的乘积:
实际光学系统的像高总是和理想成像存在偏差,这种偏差的百分比,就被定义为畸变(Distortion)。
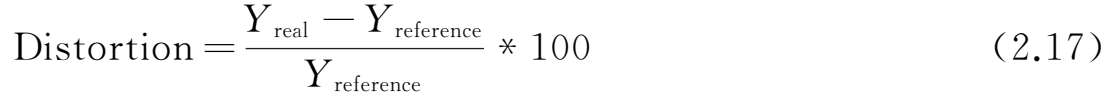
畸变有两种(图2-20):
(1)一种是实际像高大于理想像高,结果为正畸变,网格畸变的形状类似枕头,被称之为枕形畸变。
(2)另外一种是实际像高小于理想像高,结果为负畸变,网格畸变的形状类似水桶,被称为桶形畸变。
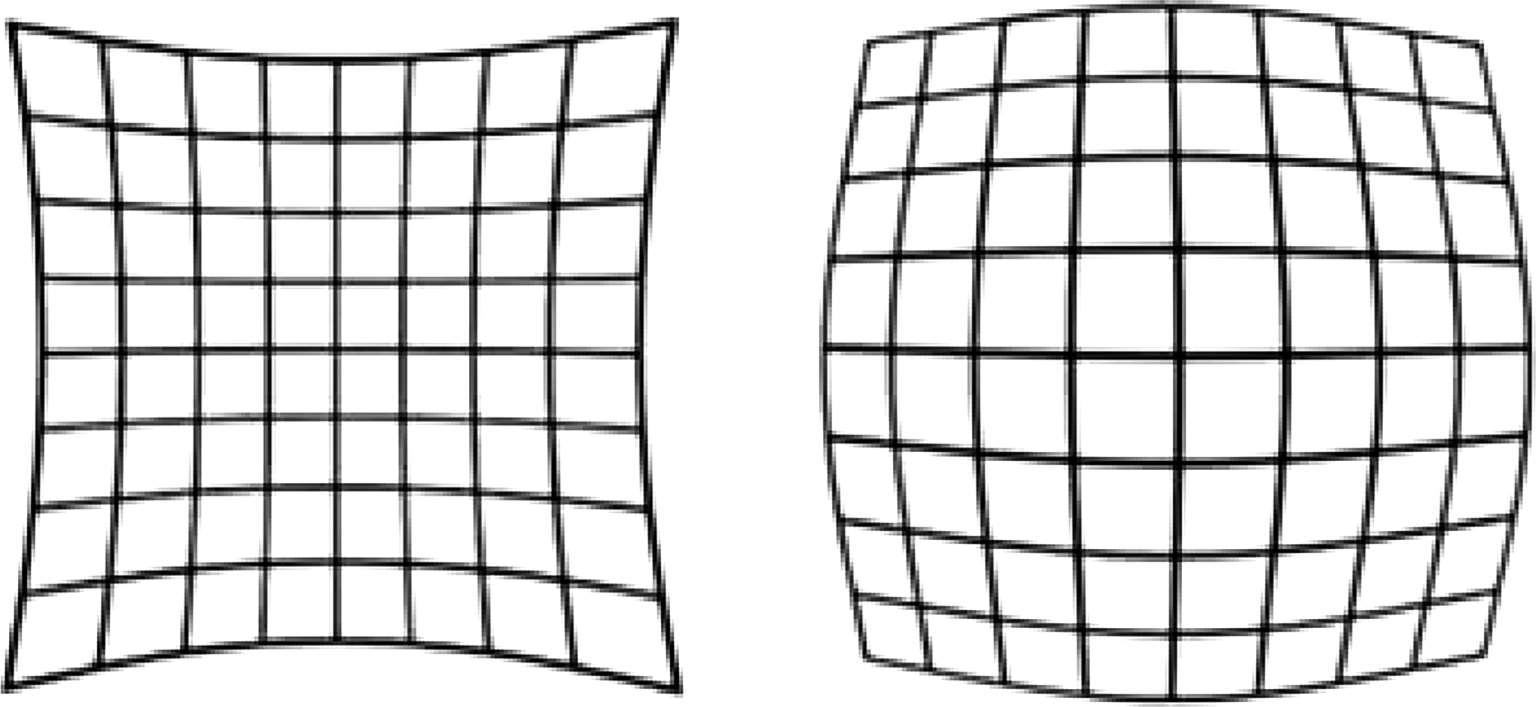
图2-20
在实际的光学镜头中,桶形畸变的情况要更加普遍。对于控制和优化畸变,CAXCAD提供了几种不同的操作数,见表2-1。
表2-1

在激光扫描系统中有一种特殊的透镜,叫做F-Theta透镜,它可以满足像高和入射角成正比:
这里的F'不是系统的焦距,而是对焦距的一种校准或缩放,通过这种校准,就可以满足上面的条件。F-Theta透镜的特点是通过控制光束的角度来线性控制激光雕刻的位置。要控制这种镜头的设计,就需要用到DISC操作数。
在手机镜头设计中,也经常会提到TV畸变,实际上是不用考虑整体几何畸变,而是控制校准的畸变,因此也需要用到DISC。
色差在折射光学系统中,工作波长在多波段情况下都会产生,因为同一种材料对于不同波长的折射率存在差异。在实际光学系统设计中,需要考虑这种像差,因为不同波长代表不同的颜色,所以这种像差被称为色差。
在多波长的光学系统中,都会有一个波长作为主波长。系统的重要参数很多都是以主波长进行计算的,例如有效焦距EFFL等。这样的参数如果采用不同的波长,结果是不同的。
如图2-21所示,在双高斯镜头的评价函数中,输入三个EFFL操作数,并且定义每个操作数的波长分别为三种不同的波长编号,给出不同的结果。这就说明系统不同颜色的光线焦点位置是不同的,这就是轴向色差。

图2-21
通常使用光线扇形图(图2-22)可以直观快速查看色差的大小。
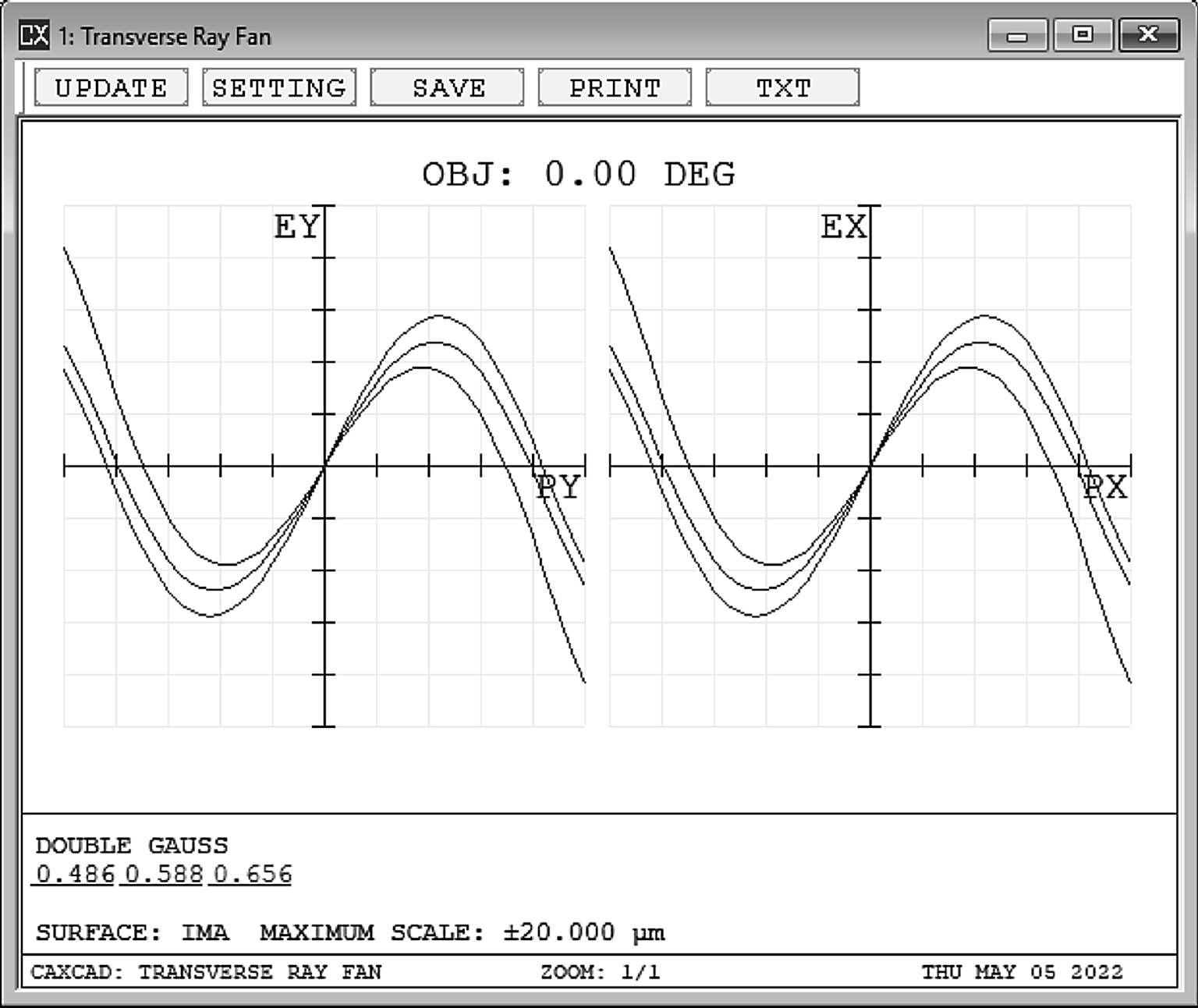
图2-22
在三阶像差中的色差,这里有两个重要的定义:
轴向色差AXCL:不同波长的近轴边缘光线在光轴上的焦距差;
垂轴色差LACL:不同波长的近轴主光线放大率不同。
色差中,除了这两种之外,还包括高级色差,例如随着不同颜色球差改变的像差——色球差等,初级像差在设计初级阶段都是重点考虑的对象。