




有关近轴光学定义,接下来将结合实例和软件来进行讲解,在本书中,通常会使用常用的库克三片式镜头或双高斯镜头作为实例文件。
在CAXCAD软件的底部状态栏上可以看到常用的基本概念,如图1-4所示。
图1-4
如果在命令窗口中,输入FIR,窗口将会快速展示重要的一阶光学数据(图1-5):
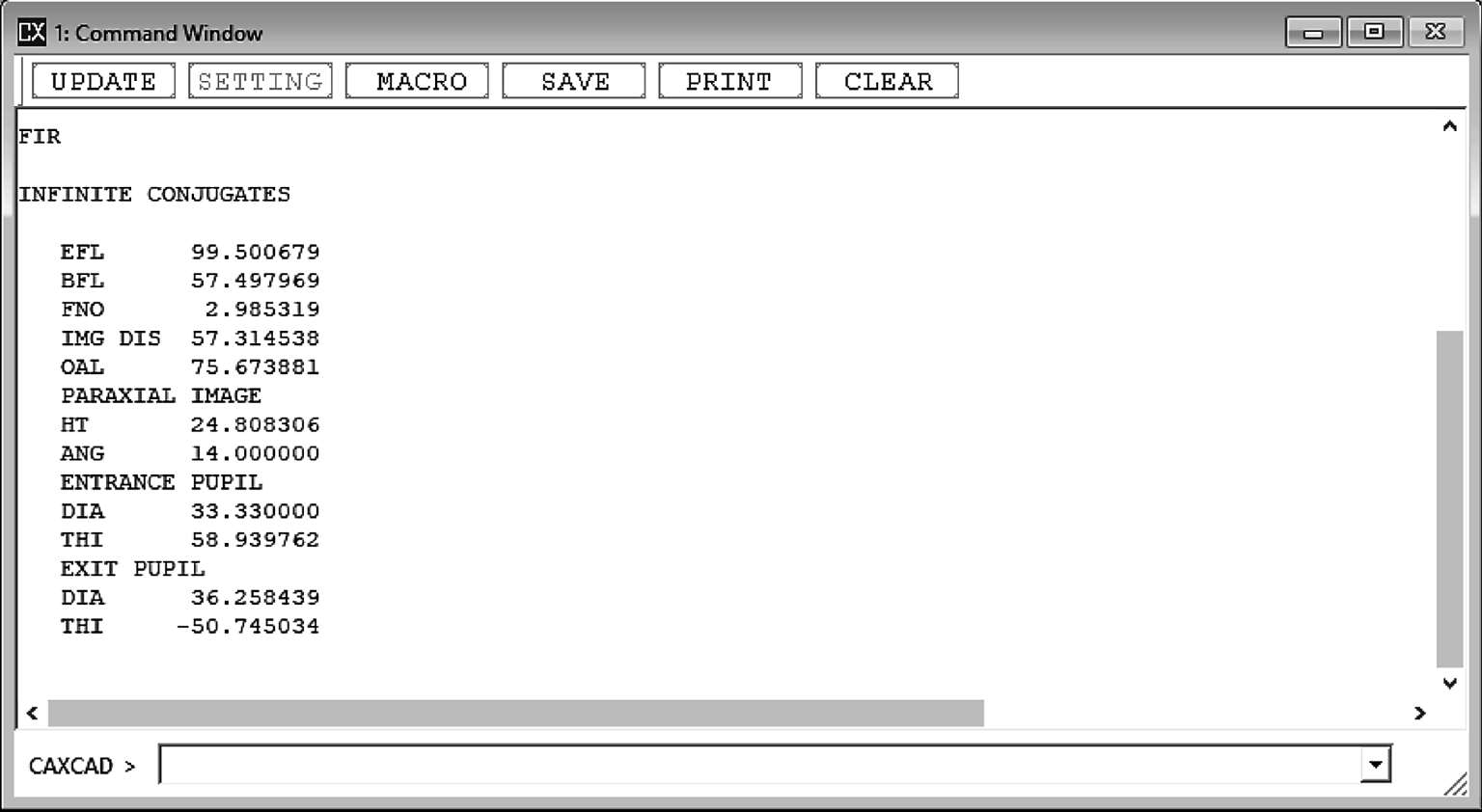
图1-5
报告菜单的系统数据System Data也可以看到一阶光学数据(图1-6):
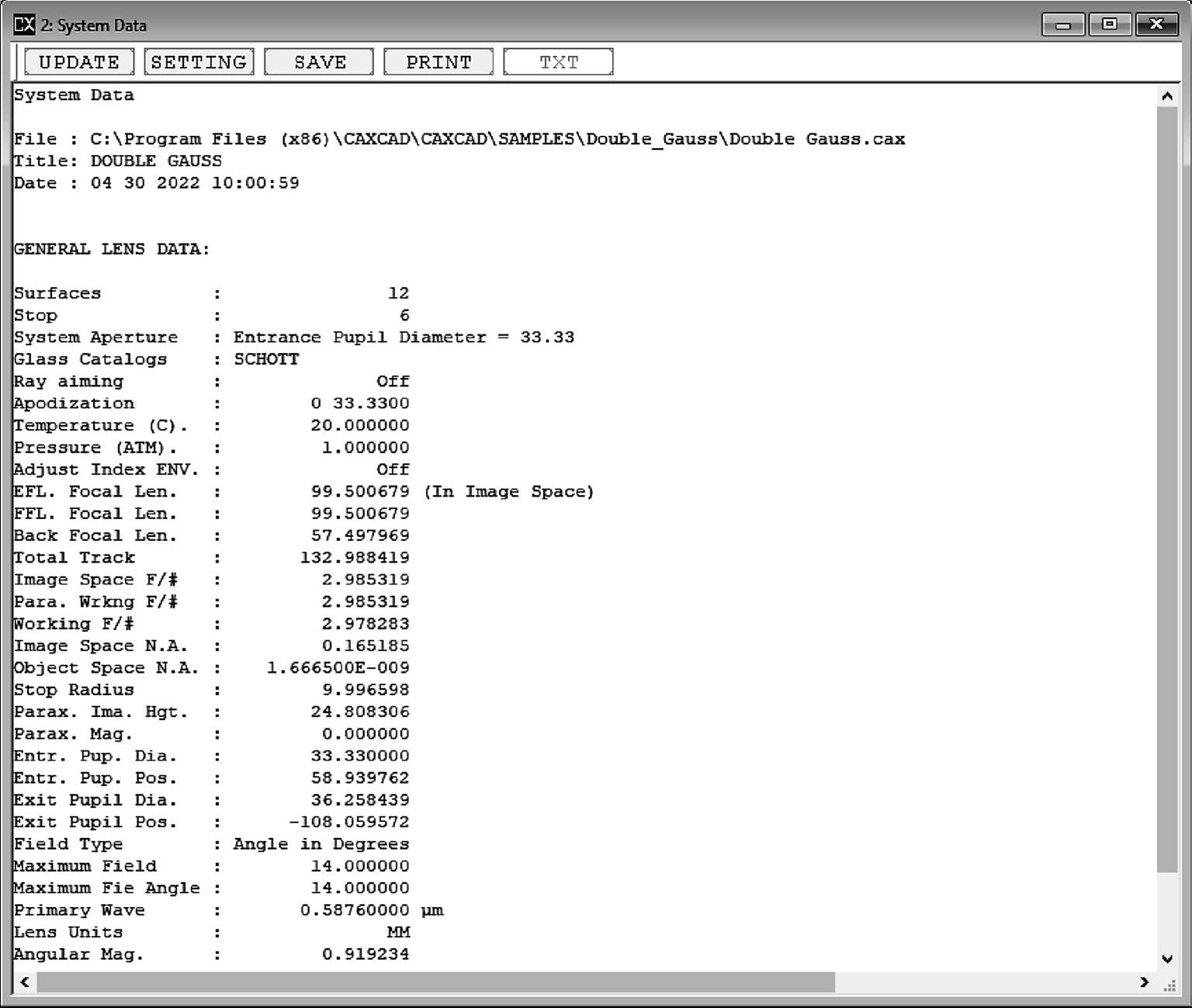
图1-6
一阶光学数据在评价函数中,输入对应的操作数同样可以查看(图1-7):
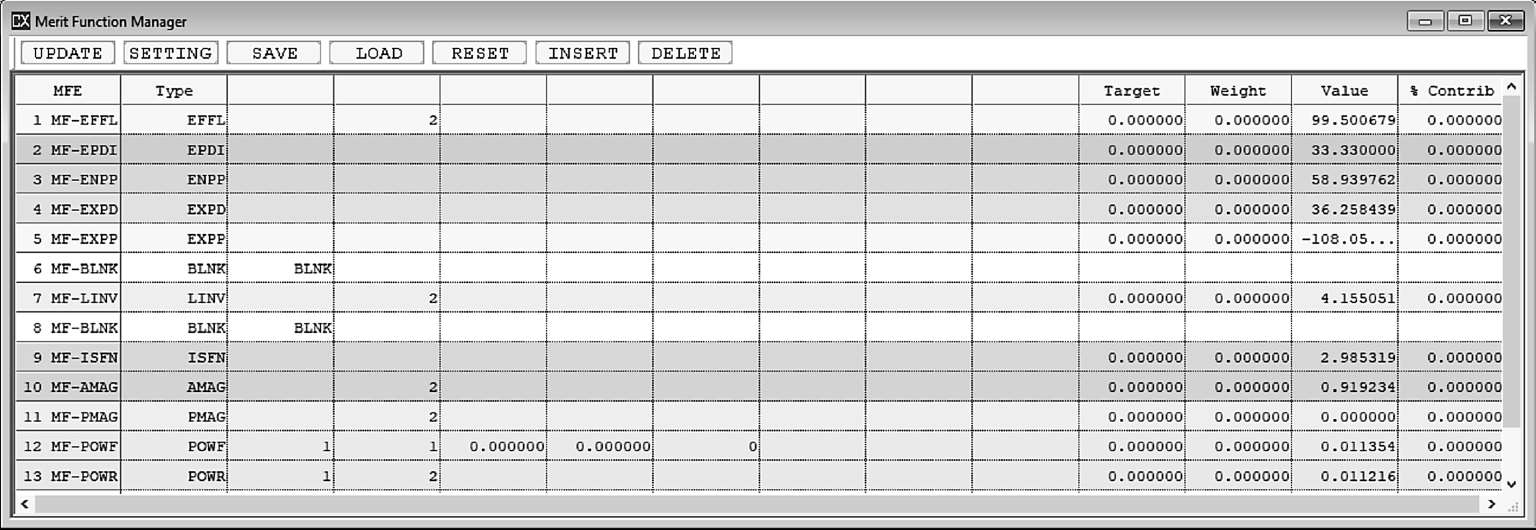
图1-7
以上仅仅是查看这些数据的不同方法,在CAXCAD软件中,对这些概念进行了分类。如图1-8所示,打开自动优化工具,在横向色差列表里可以看到,重要的一阶光学定义都在这里。
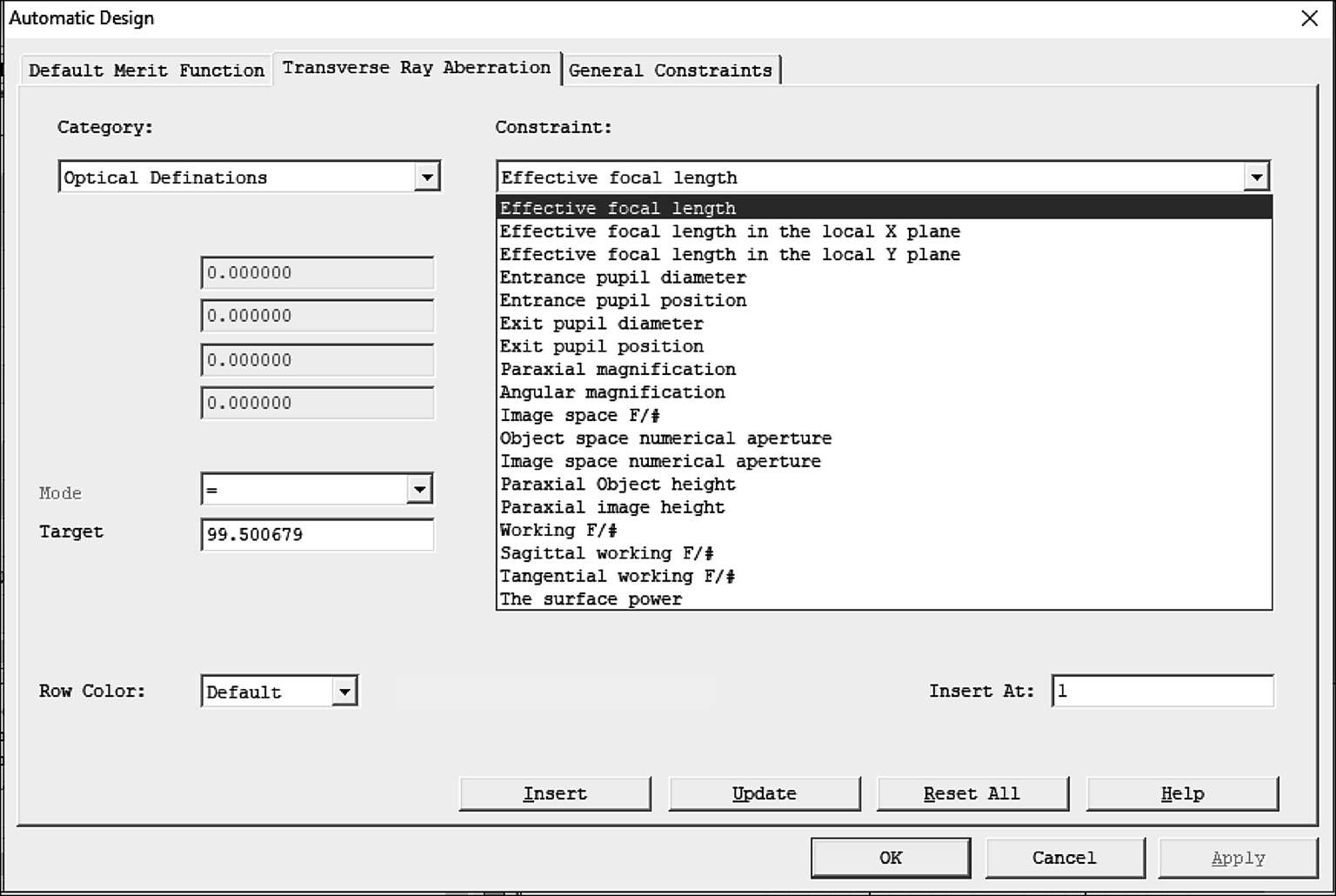
图1-8
利用近轴近似进行光线追迹(图1-9),可以获得近轴光线的角度和位置。
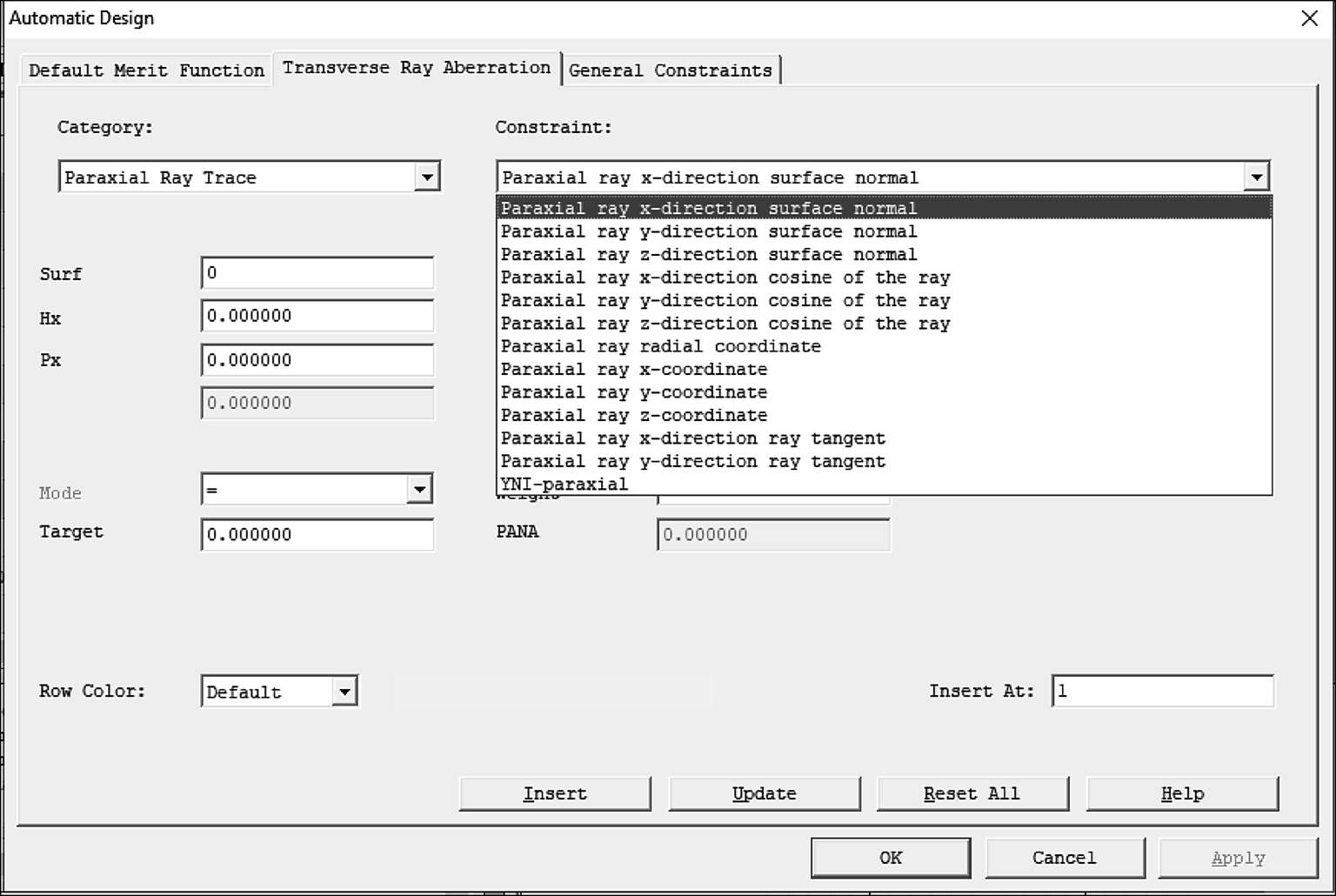
图1-9
通过自动优化工具,列表中每个定义实际上都可以作为一个优化操作数快速插入到评价函数中,同时可以在图上看到这个定义简写的四个英文字母。关于操作数的使用,在优化章节中将会详细说明。
在光学CAD软件中,很多的定义并不会直接使用公式进行计算,而是依赖于光线追迹的结果。这里就需要提到“基础光线”的概念。所谓基础光线本质上是真实光线,只是角度很小,光束传播需要按照真实光线的折射定律进行,而不是采用一阶近似。对于近轴光学的很多定义,要利用基础光线数据而不是近轴光线进行计算。所以下面提到的定义或概念都是光线追迹后的结果。
放弃使用公式,而利用基础光线进行计算有很多好处,因为通常公式的计算只适用于共轴光路或者理想薄透镜。而实际的情况是需要精确地知道整个真实光学系统的参数。
有效焦距是最容易理解的一个概念,它表示如果一束平行光进入光学系统,近轴光线的后主面到达近轴焦点的距离,针对没有像差的理想薄透镜(图1-10)来说,就是透镜到达焦点的距离。
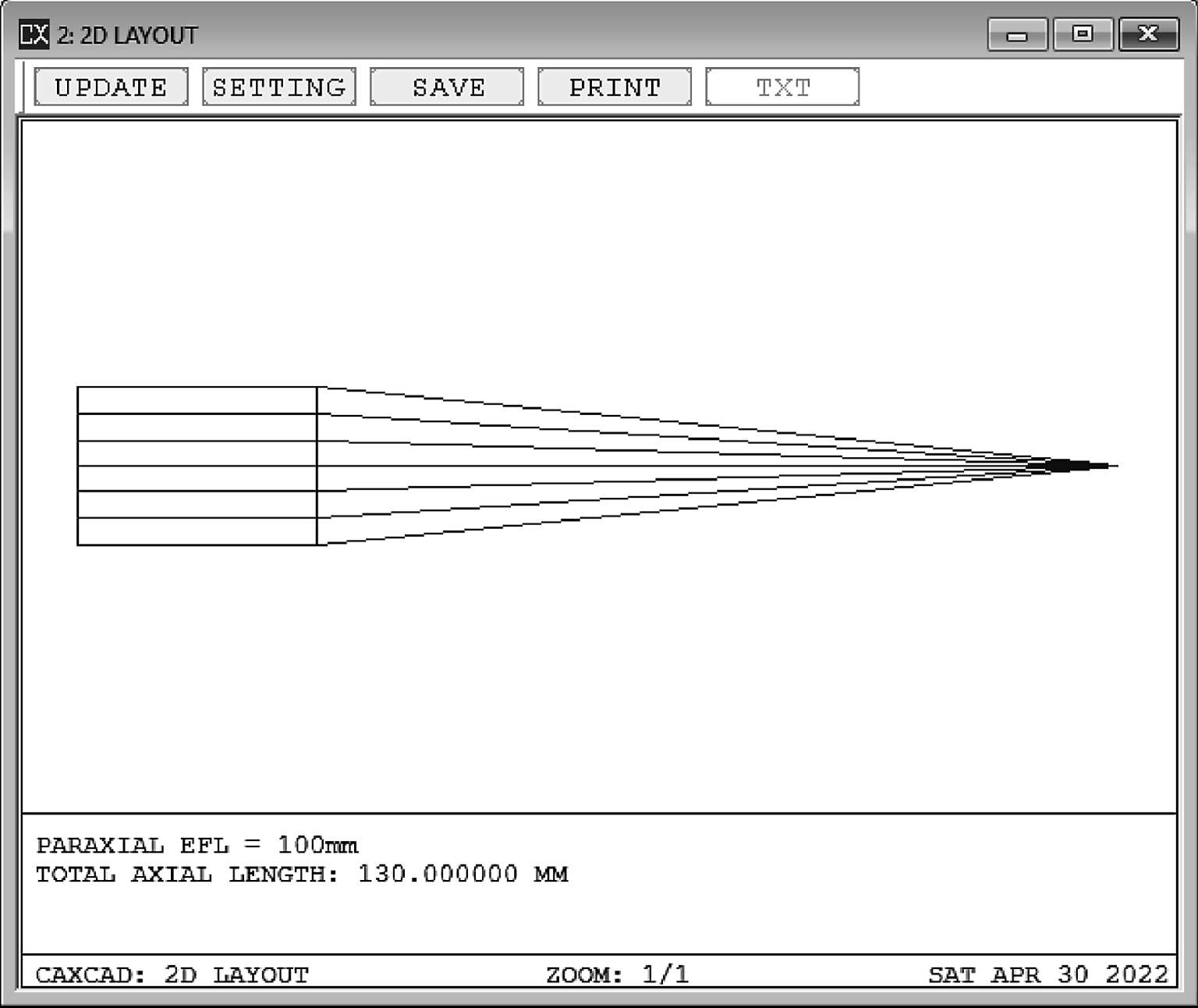
图1-10
在实际的光学系统中,就需要着重强调“近轴”,因为此时计算焦点的位置是以近轴光线为基准的。建立一个焦距100 mm,入瞳为25 mm的单透镜(图1-11~图1-12):

图1-11
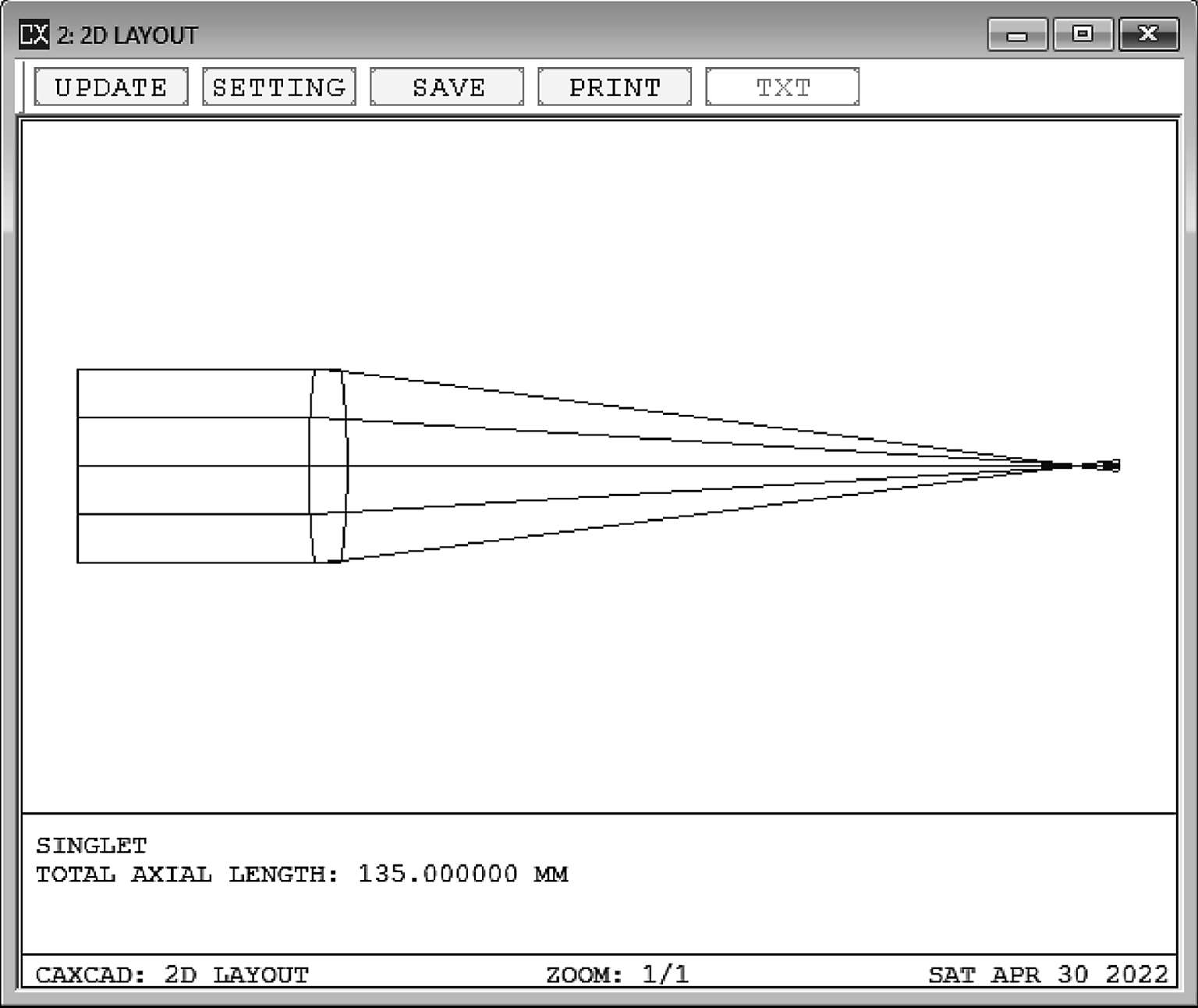
图1-12
实际的透镜光线在焦点处通常存在球差,在光线聚焦附近来自不同孔径的光线具有多个焦点(图1-13),而计算基准是近轴焦点。
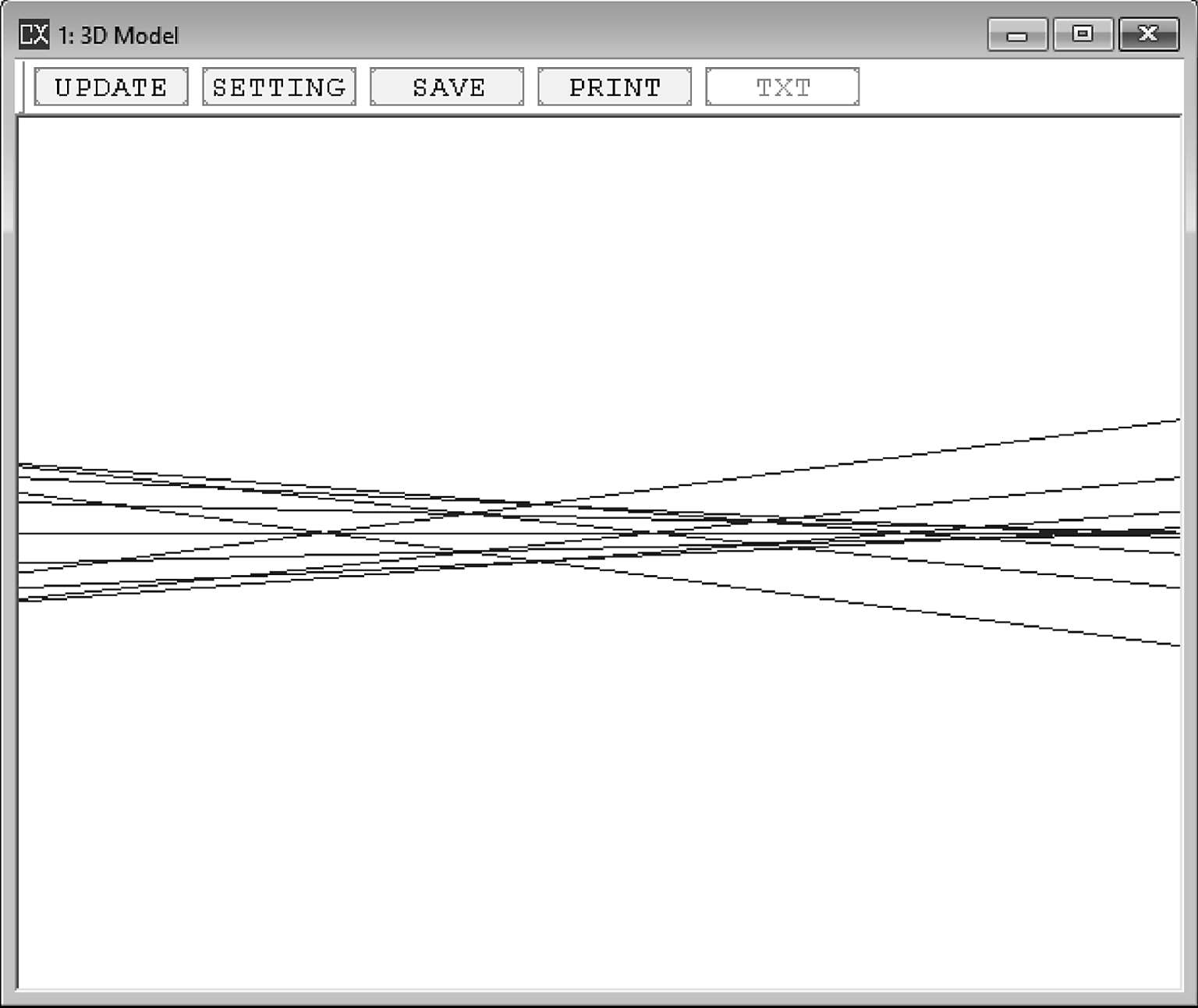
图1-13
如何才能快速找到这个焦点的位置呢?这里可以利用第三个面厚度求解的方法(图1-14):
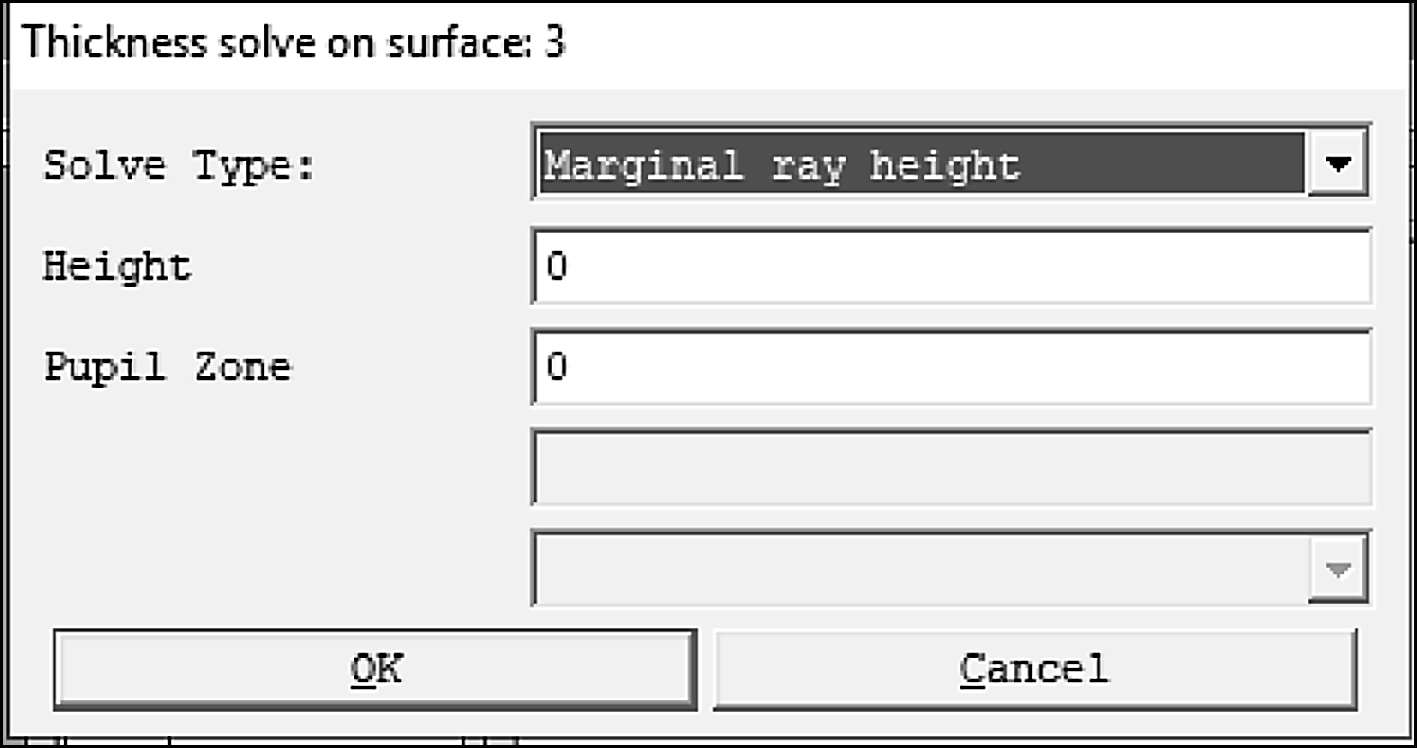
图1-14
光线的Pupil Zone为0就表示是近轴光线,高度Height为0表示聚焦在轴上,由此计算出来的厚度95.597 596就是近轴焦点的位置(图1-15)。

图1-15
可以利用评价函数演示焦距的计算,这里使用基本光线,也就是近轴的真实光线。采用EFFL可以直接读取有效焦距的数值97.258 108,给定光线的高度为0.000 012 5,作为一个近轴的真实光线高度,因为入瞳的直径是25 mm,半高度是12.5 mm,
所以P y 作为归一化光瞳高度为0.000 001(图1-16)。利用RAYB可以获得光线在镜片最后一个面上Y方向的方向余弦为-0.000 000 128 523 989。然后根据三角函数的关系,就可以计算出有效焦距:


图1-16
光阑(STOP)在物空间成的近轴像就是入瞳,它的直径就是入瞳直径。
近轴入瞳相对于第一个面的距离,所谓第一个面指的是编号为1的面。
在实际光学系统中,无论光阑是在物方还是在像方,所成的像都是一个虚像。实际上在光路中是找不到这个器件的,但是仍然有方法在光学软件当中展示它们,这里可以用经典的双高斯镜头作为实例。
打开双高斯镜头如图1-17所示:
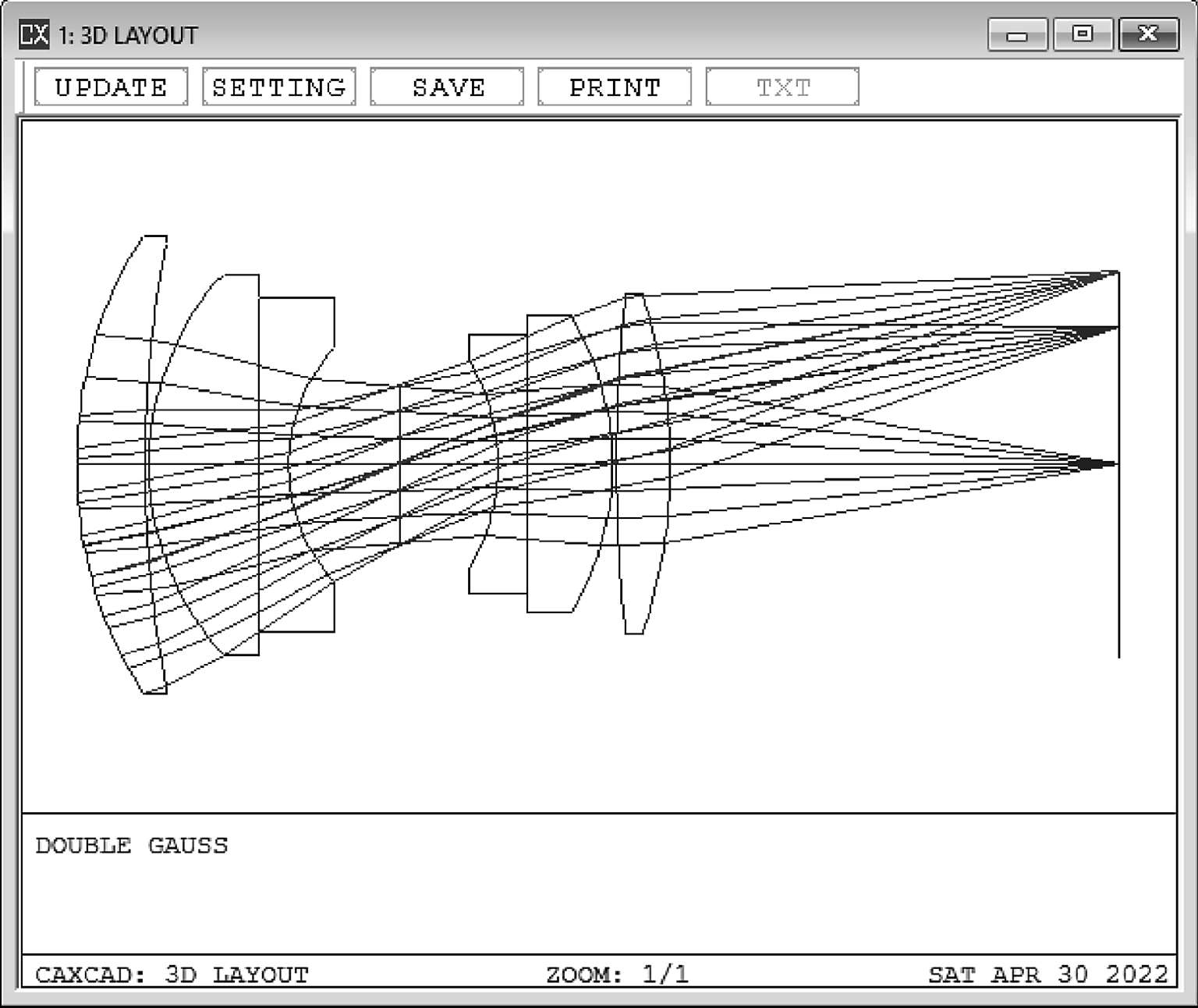
图1-17
可以利用前面提到的任意一种方法来查看一阶光学数据中的入瞳位置,这里选择的FIR命令窗口,并确认数值是58.939 762(图1-18)。接下来要在光学系统中看到它,就需要用到一种方法,这种方法被称之为虚拟传播,所谓虚拟传播言外之意就是可有可无,并且对光学系统最终的成像没有影响。
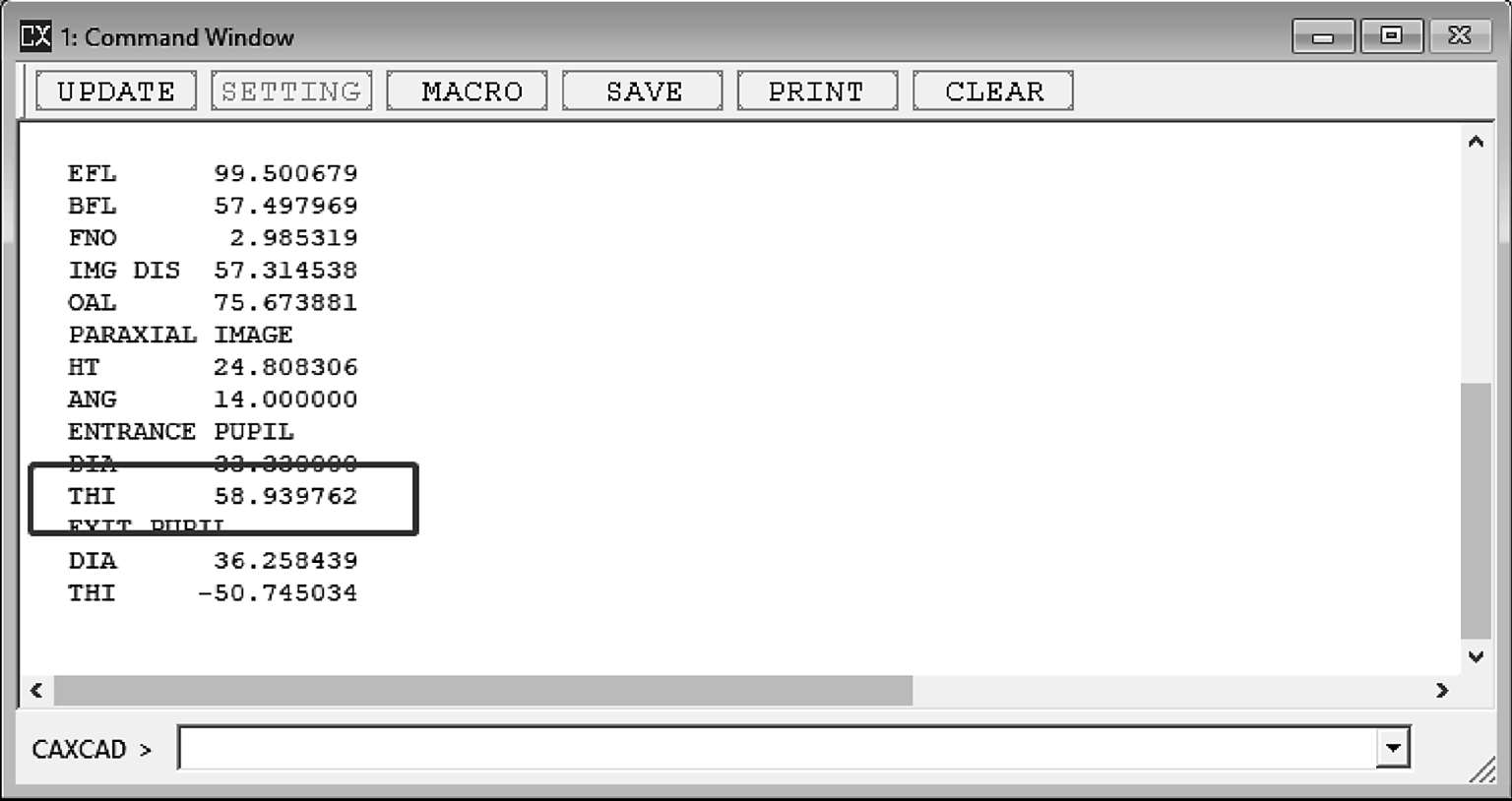
图1-18
修改透镜数据编辑器,只需要在镜头前方插入两个空的面并定义厚度,如图1-19 所示:
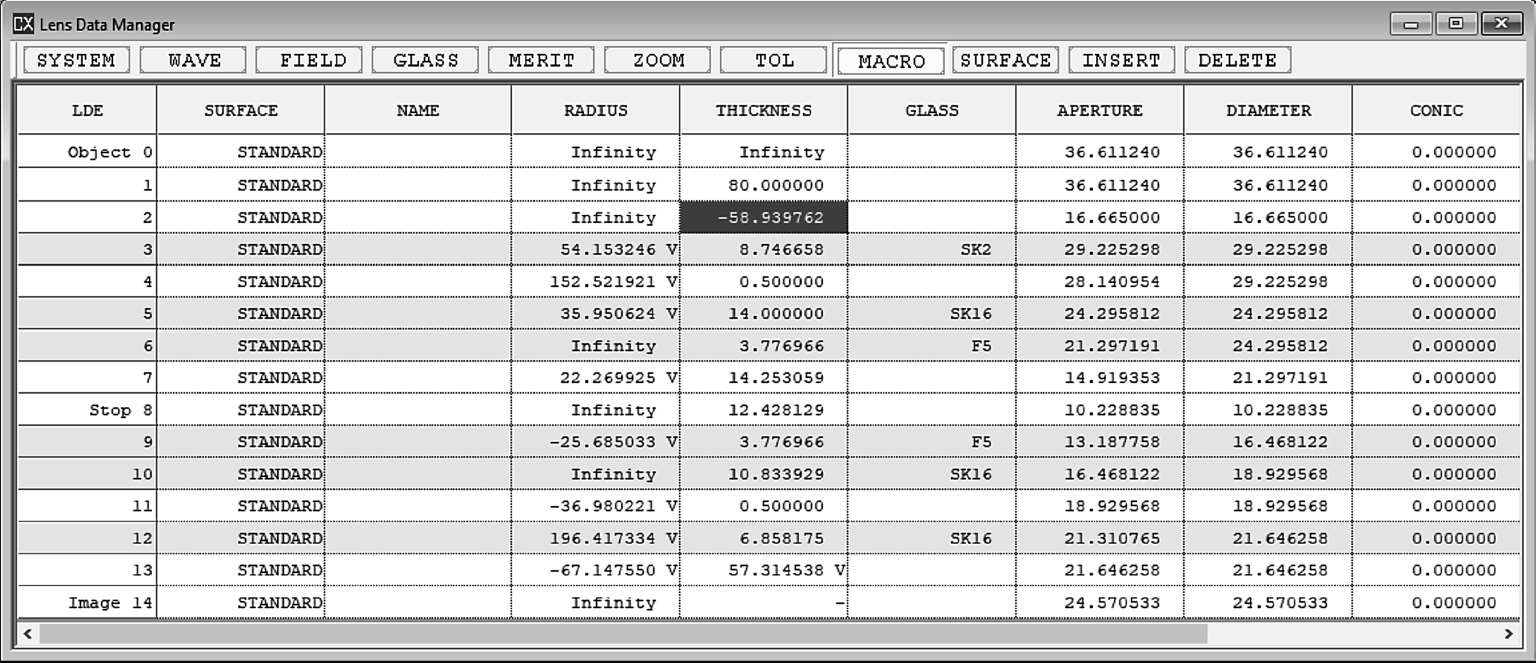
图1-19
上图中80 mm的厚度是为了展示镜头前光线的入射,-58.939 762则是展示出了相对镜头第一个面(此时编号为3)的位置,也就是入瞳位置。
因为光阑面的编号是8,所以在3D Layout外观图形中,将显示范围调整为1-8(图1-20)。
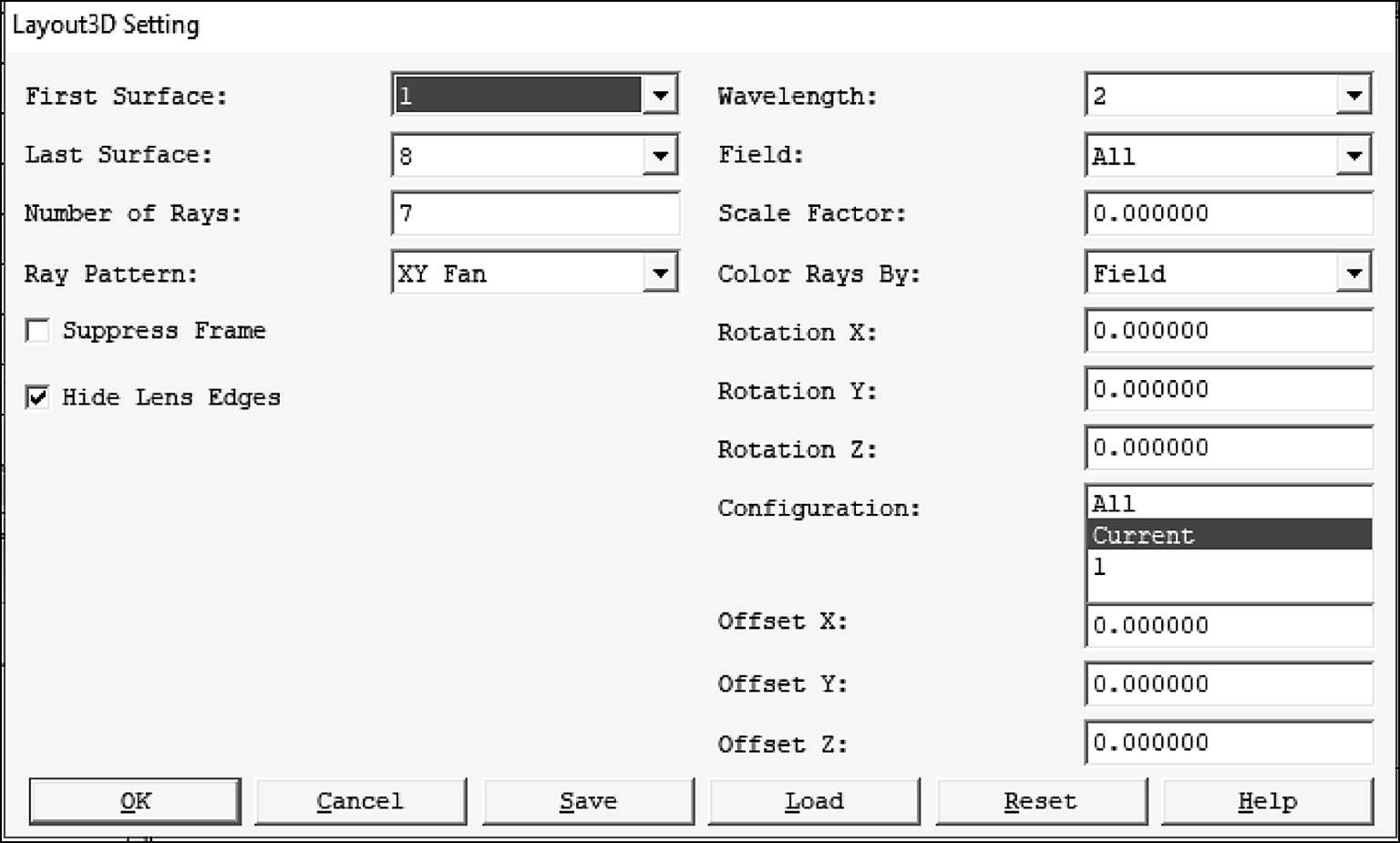
图1-20
于是通过入瞳位置(图1-21),就可以清晰看到不同视场的光线在这个位置交汇,这就是光阑(STOP)面所成的虚像。
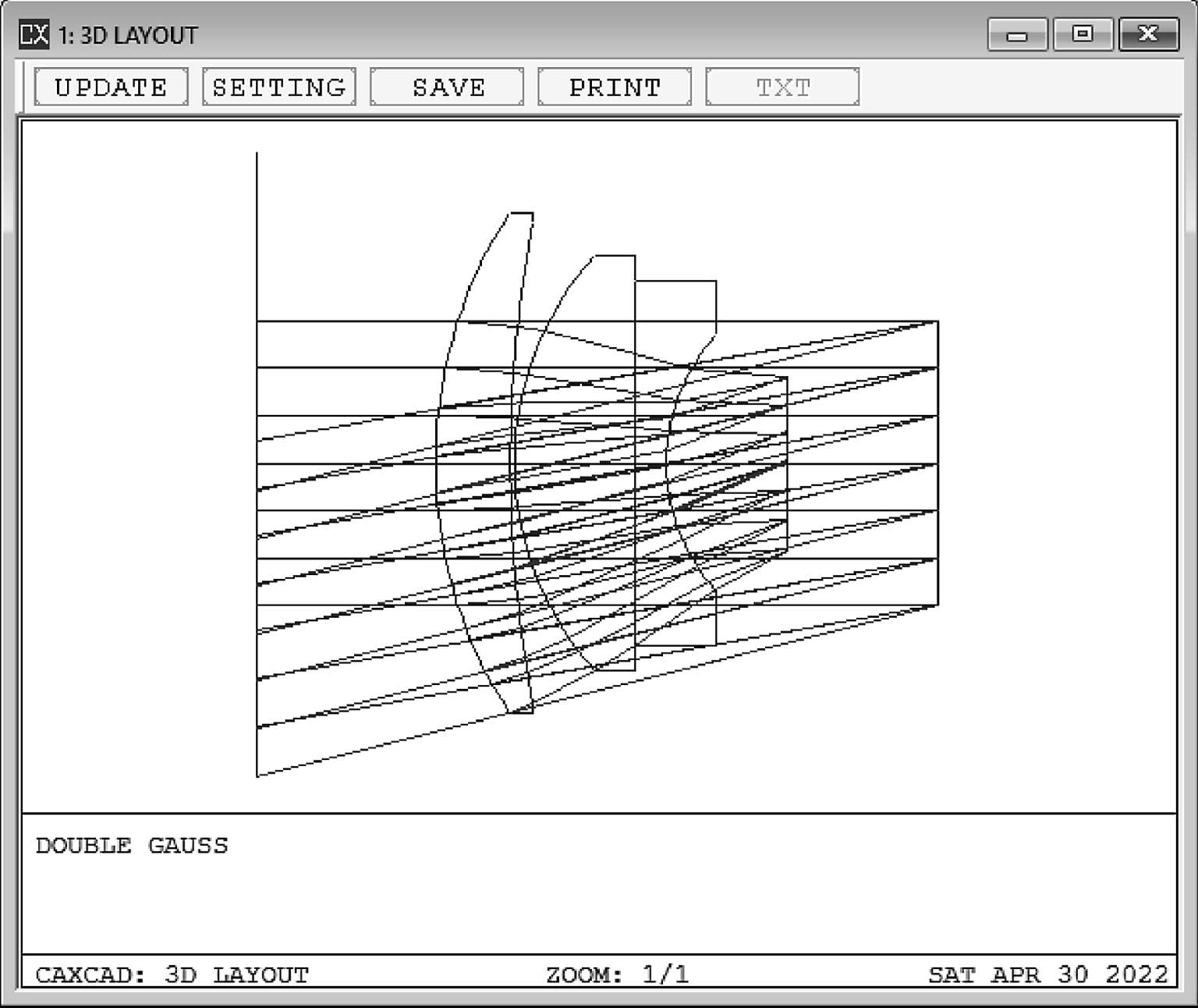
图1-21
光阑(STOP)在像空间成的近轴像就是出瞳,它的直径就是出瞳直径。
近轴出瞳相对于像面的距离就是出瞳位置。
接下来利用同样的双高斯镜头来展示出瞳位置,在一阶光学数据中查找并确定出瞳的数值为108.059 572,这是相对于最后一个面的。在像面前插入一个面,并将厚度设置为出瞳位置,如图1-22所示:
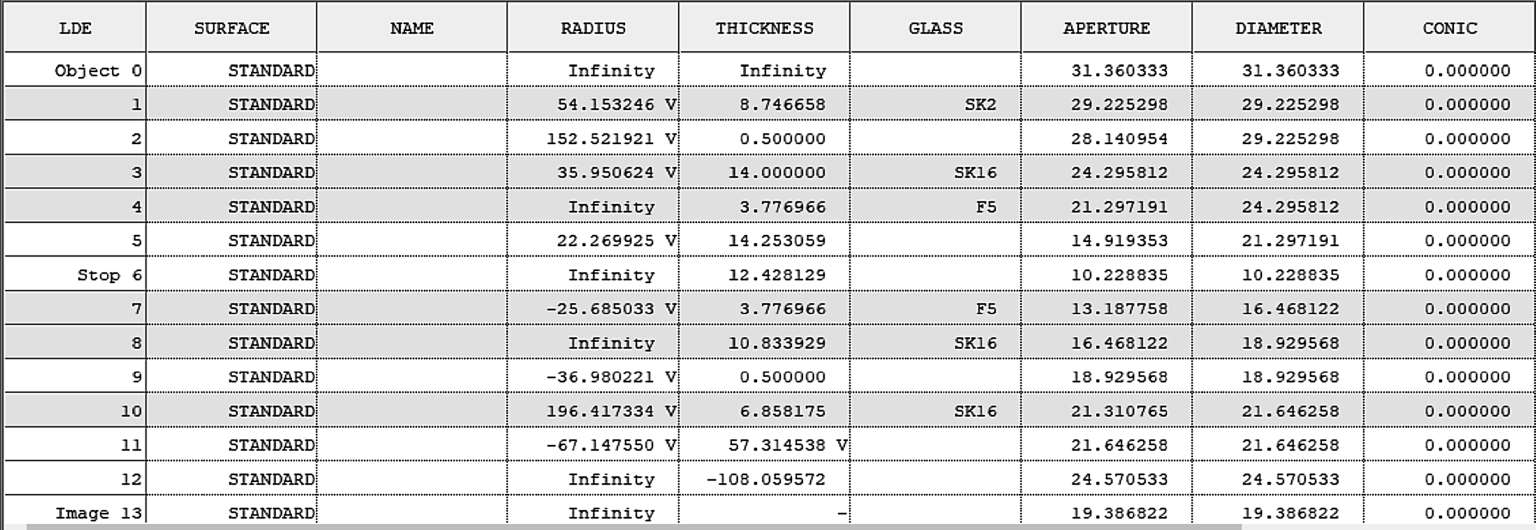
图1-22
此时的光阑面的编号是6,将3D Layout外观图形中的显示范围调整为6~13,光瞳位置就可以看到了(图1-23)。
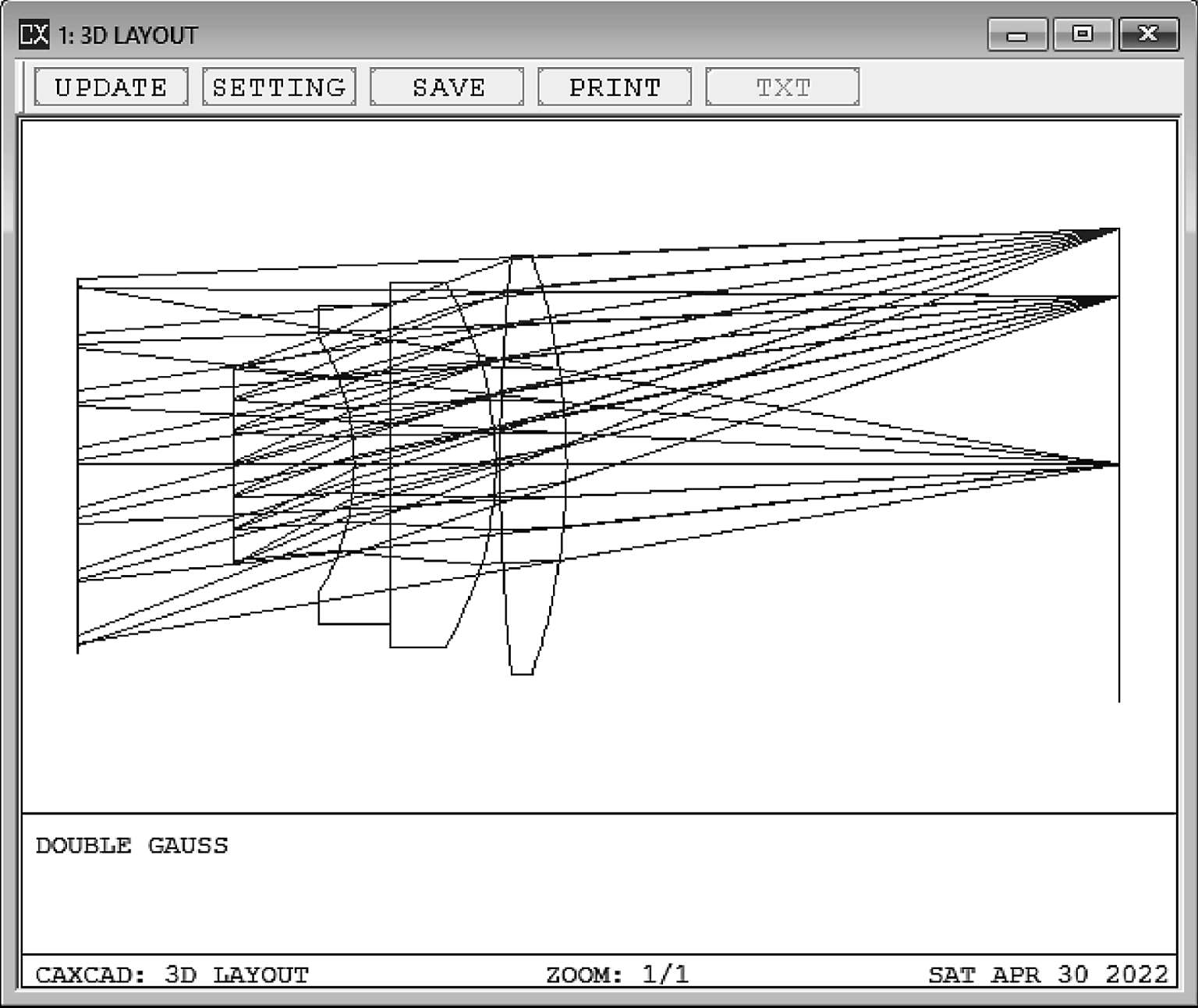
图1-23
在出瞳的展示中(图1-23),会发现一个很明显的问题,代表不同颜色不同视场的光线没有交汇在一起。这是因为出瞳位置是以近轴计算的,在光瞳的中心位置,代表绿色的第2视场要比红色的第3视场的光线更加接近中心。
另外还有一个更快捷的方法——厚度求解,如图1-24所示。将像距的厚度57.314 538进行求解计算,求解算法基于光瞳位置。
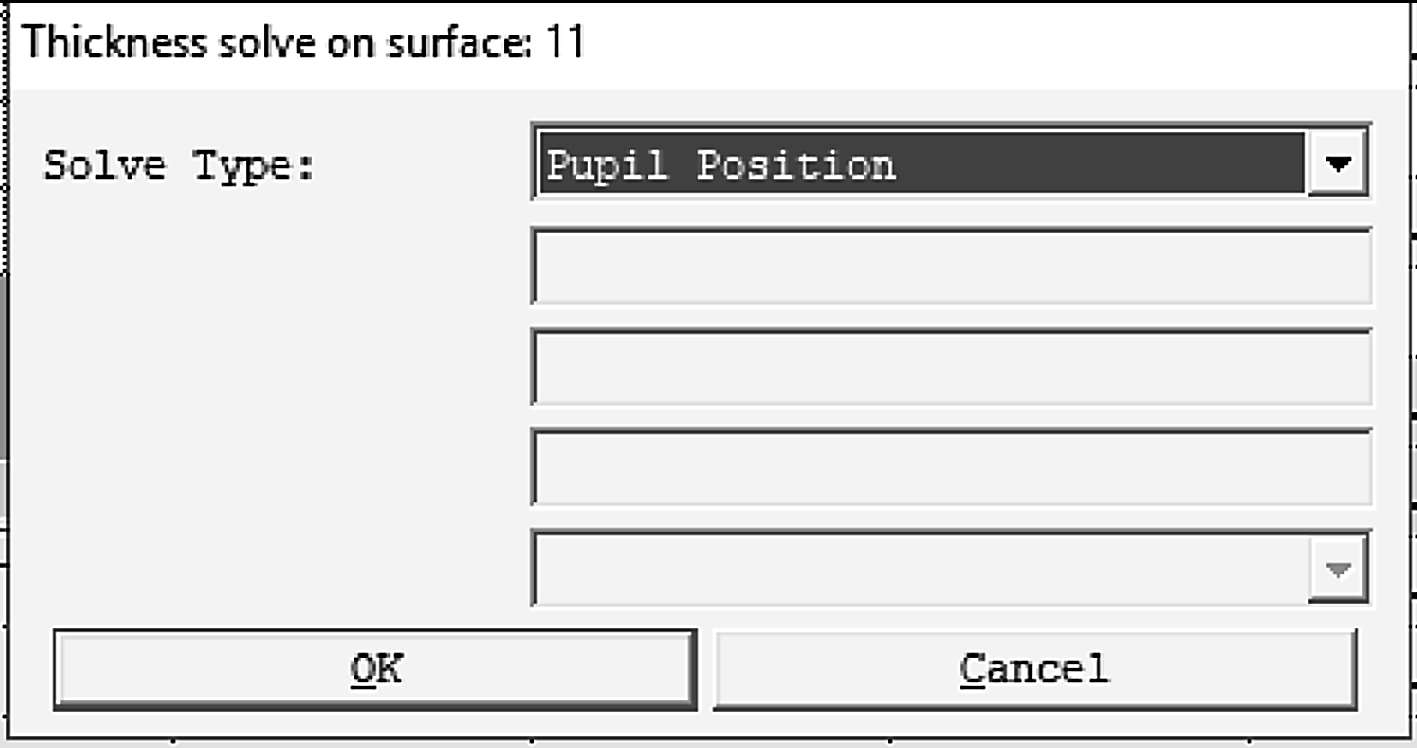
图1-24
这里的光瞳位置指的就是出瞳位置,系统会自动将像面设置在出瞳位置上。当然这种求解也可以直接在新插入的面上进行,获得的结果是一样的。
在物像有限共轭系统中,近轴放大率为近轴像高和近轴物高的比值。
角放大率为近轴像空间主光线角度和近轴物空间主光线角度之比。
这里需要讨论一下关于放大率的知识,近轴放大率属于线性放大率,通常用于快速控制镜头物像高度的比,例如控制显微镜或图像采集镜头的倍率等。在近轴放大率无法计算的情况下,AMAG就可以派上用场,控制无焦光学系统的角放大率,例如伽利略转鼓、枪瞄镜头和望远镜等。可是仍然需要注意的是,这里的计算都是近轴计算,随着视场角度增大,这个计算结果的误差也会加大。
下面把双高斯镜头做一个变换,将物面厚度设置为200(图1-25~图1-26):
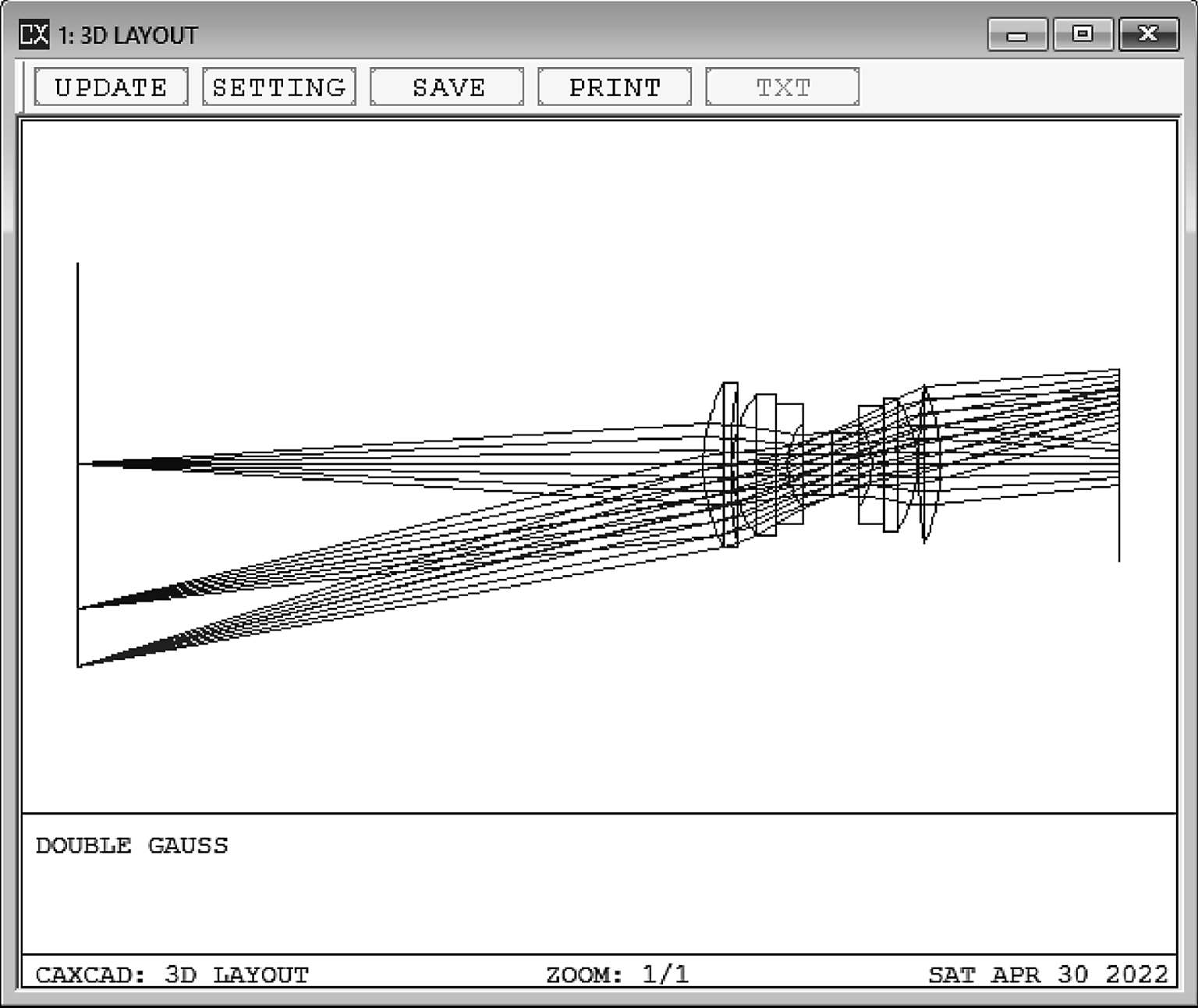
图1-25
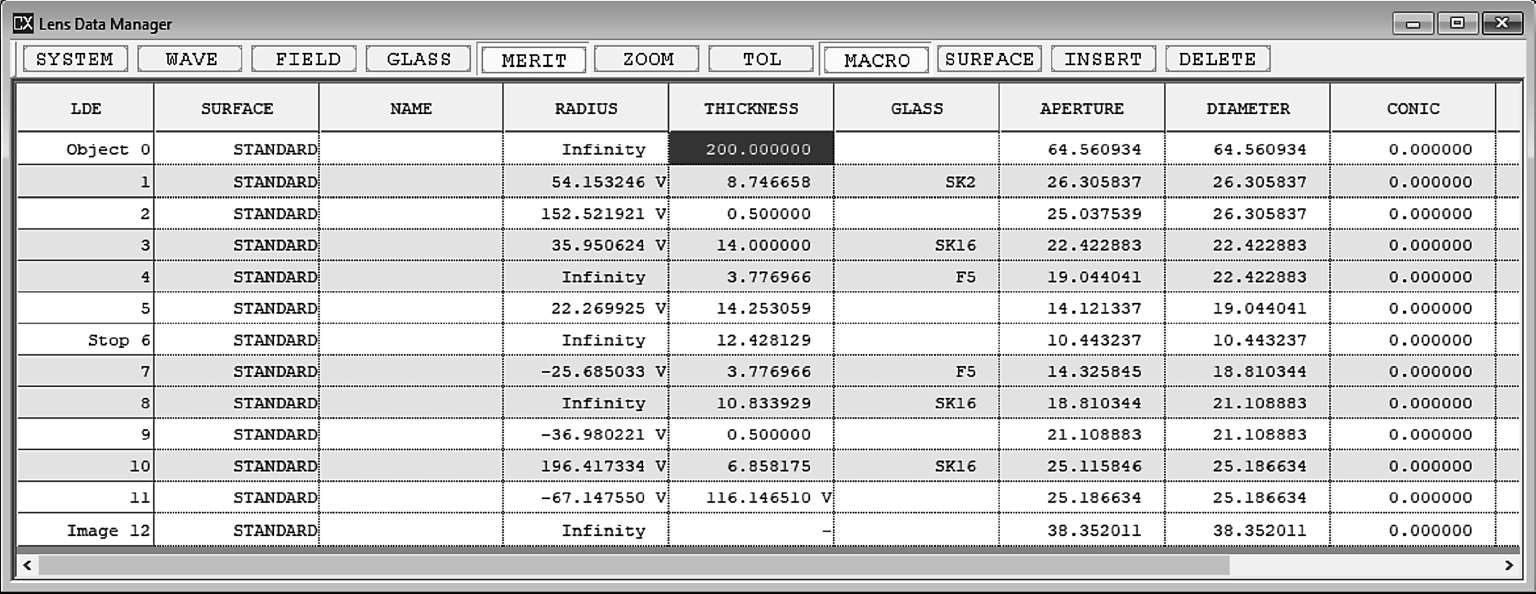
图1-26
优化菜单(Optimization)上找到快速聚焦工具(Quick Focus)并执行,像面的距离会自动被优化到默认的最小光斑。
快速聚焦后获得了一个物像共轭的系统(图 1 27),这时就可以使用近轴放大率PMAG了。在评价函数中输入PMAG,可以看到近轴放大率是-0.594 121(图1-28),负值表示成的是倒像。
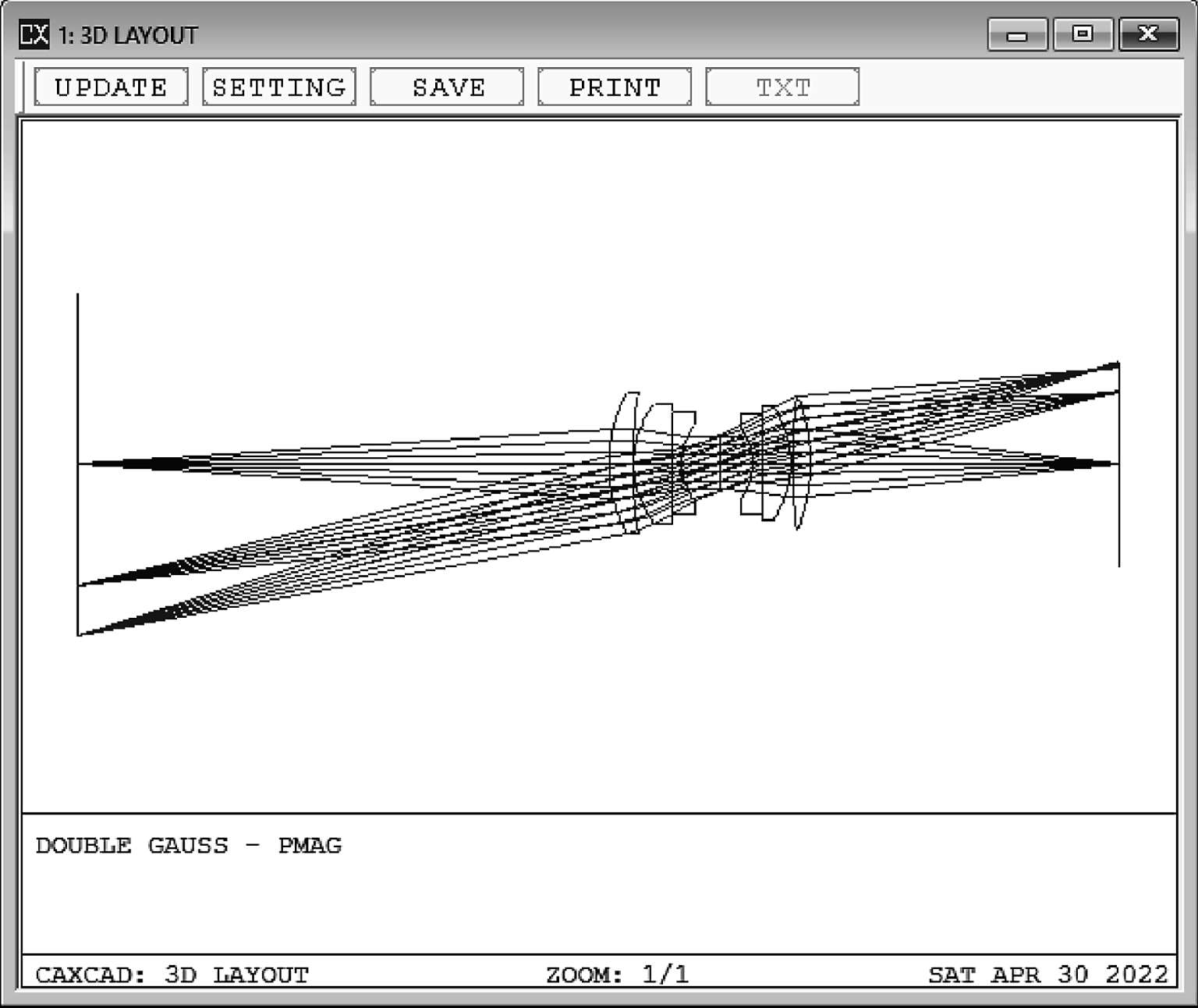
图1-27

图1-28
刚刚讲过,这个数值是近轴计算,所以针对实际的光学系统一定存在误差,真实的放大率是多少呢?下面利用真实光线追迹进行对比和计算(图1-29)。
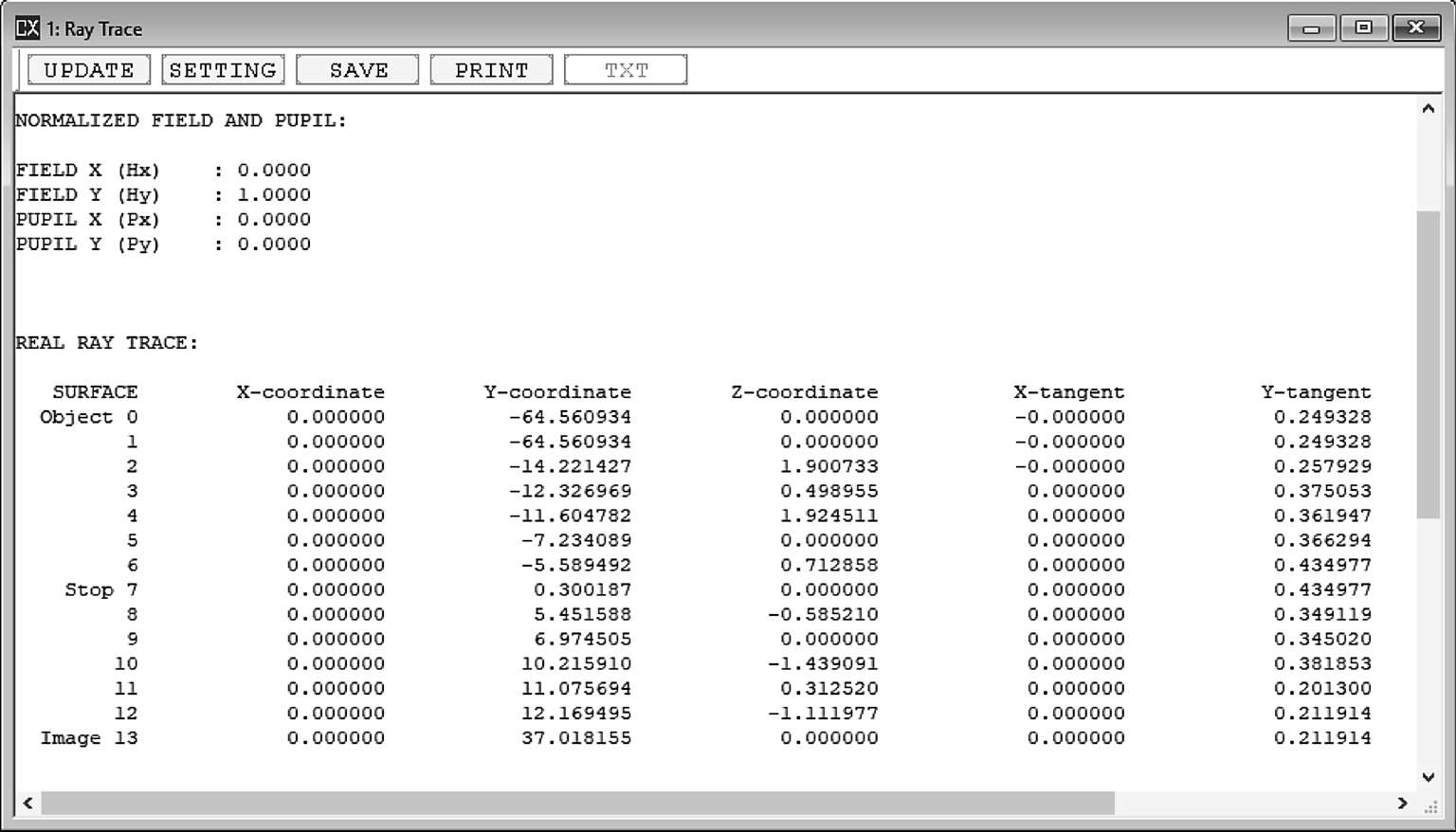
图1-29
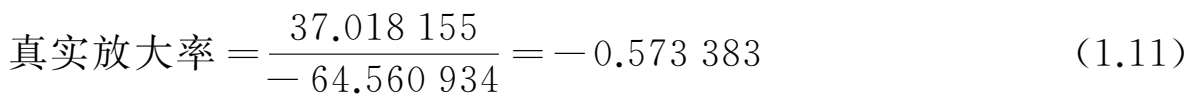
由此可知,近轴放大率可以快速近似获得系统放大率,但是和真实放大率相比,还是具有一定的差别。如图1-30所示,在评价函数中,利用Y方向的真实光线高度操作数RAYY(或REAY)分别获取像高和物高,再用DIVI计算它们的商,可以直接获得真实放大率,并且可以对这个比值进行控制和优化。

图1-30
同样的道理,对于真实的角放大倍率,可以采用物方和像方的操作数RANG的比值来计算和控制。
像空间F/#是有效焦距和入瞳直径的比。这里有一个假设,无论这个镜头工作在什么样的场景,都是以平行光入射为基准进行计算,这是因为作为前提的有效焦距就是这样定义的。

这个参数是镜头设计中通常要求的指标,根据像空间F/#,设计者可以快速判断镜头设计的难易程度。这个数值越大,镜头获得的光照就越小,几何像差就越容易被矫正,受到衍射极限的影响和限制也会越大。这个数值越小,镜头就可以获得越多的光能量入射,但是几何像差就会越大并越难控制。
在系统参数设置中,孔径类型可以直接指定像空间F/#如图1-31所示:
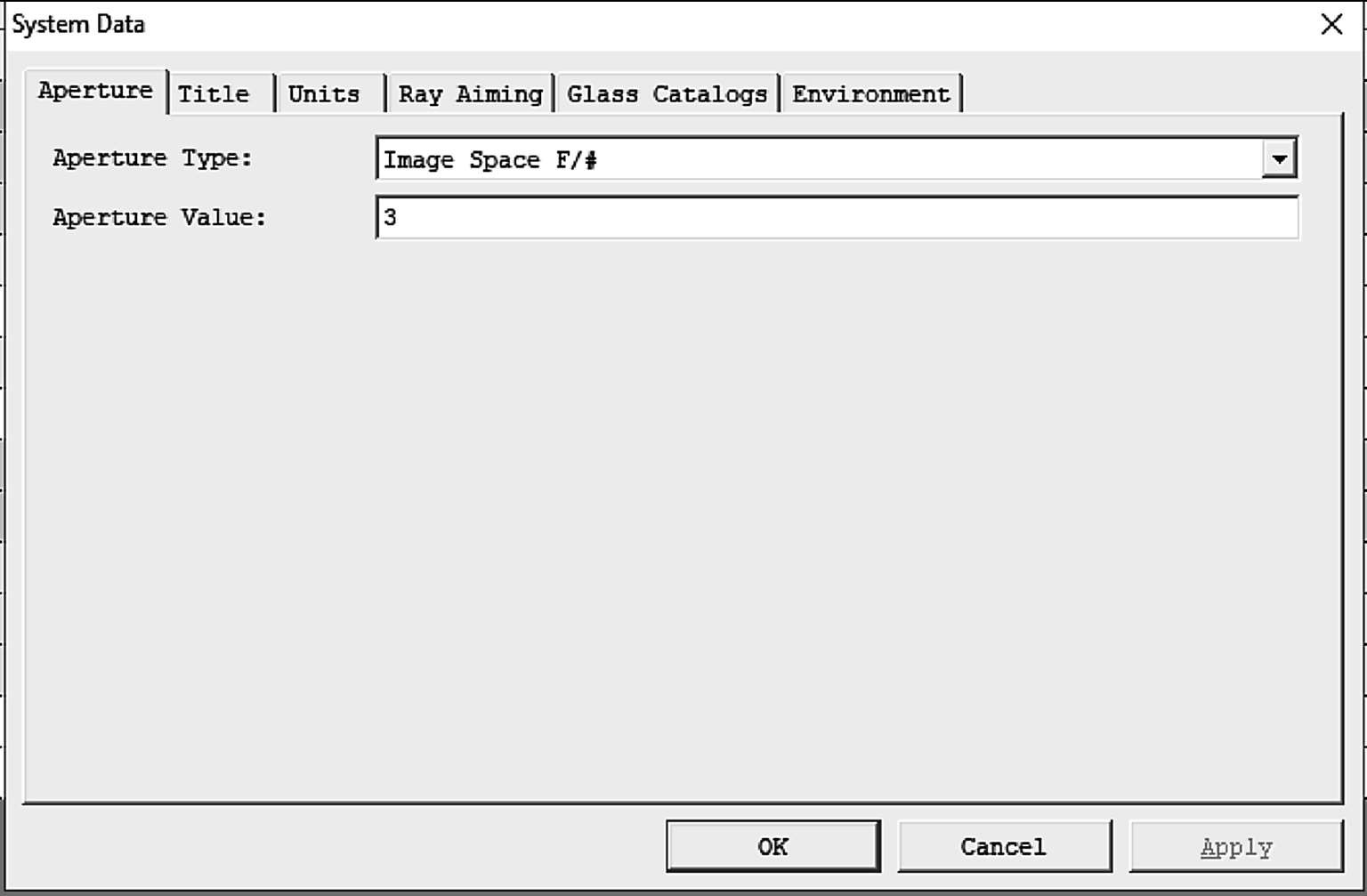
图1-31
其中,使用最多的还是利用最后镜头面上的曲率求解(图1-32),这种方法非常方便,而且配合入瞳直径的设置,控制了镜头的有效焦距。这样的好处是评价函数中少了一个操作数,从而可以将优化的更多权重分配给成像质量操作数。
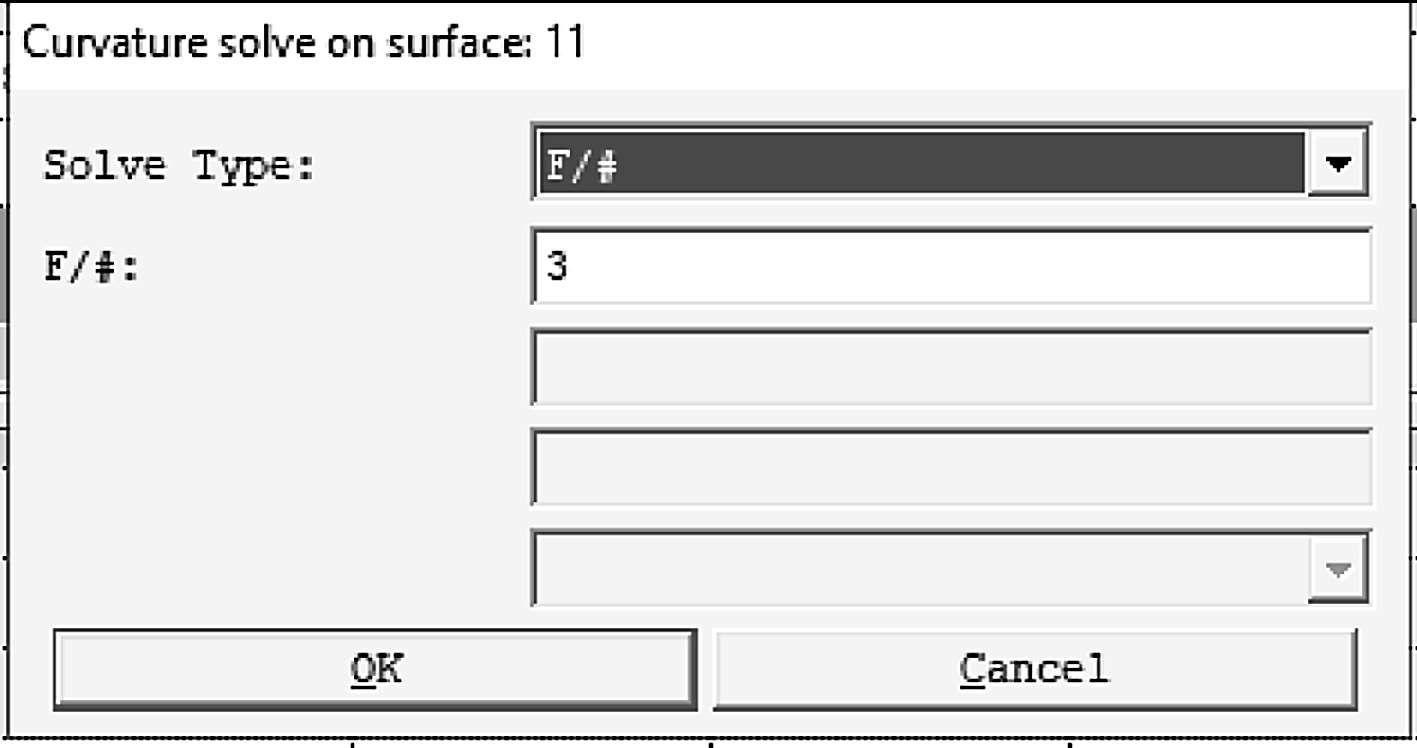
图1-32
近轴工作F/#的定义如下:

其中θ是像空间近轴边缘光线的角度,n是像空间的折射率,对于非轴对称系统,θ是中心光线和不同方向边缘光线的角度平均值。
工作F/#的定义如下:

其中θ是像空间真实边缘光线的角度,很显然如果角度很小,工作F/#值将是一个很大的数,此时默认会给出10 000的数值,在光学系统计算点扩散函数PSF和调制传递函数MTF时也是如此。n是像空间的折射率,对于非轴对称系统,θ是中心光线和不同方向边缘光线的角度平均值。
工作F/#不是近轴计算,而是基于真实光线,所以工作F/#可以体现出光学系统的真实像方工作情况,这个定义放在这里,可以让读者对不同F/#的定义加以区别。
这里有两个数值孔径,分别是物方数值孔径OBNA和像方数值孔径ISNA。它们分别使用近轴边缘光线角度的正弦值乘以对应物空间或像空间的折射率。
物方数值孔径OBNA可以用来控制物方物点的张角。CAXCAD系统孔径的设置中有这个选项(图1-33):

图1-33
已知镜头的像方NA,例如显微物镜,就可以知道放大倍率。但在实际设计中,以上两个数值孔径是无法满足要求的,因此就需要真实的NA值。如图1-34所示,可以采用RAYC(或REAC)获取真实边缘光线的方向余弦,再用ACOS计算角度,用SINE计算正弦值,这样就可以获得真实的像空间NA了。
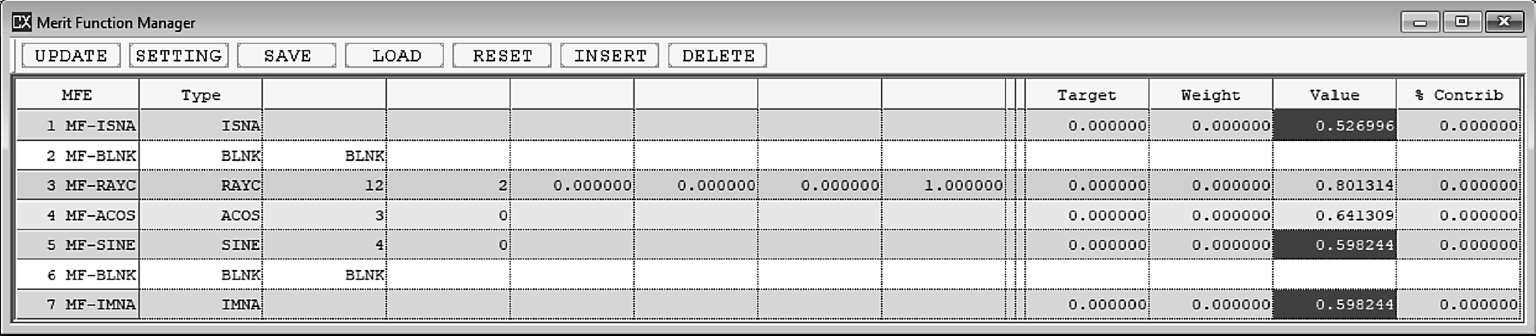
图1-34
从上面的数值可以看到ISNA像空间NA是0.526 996,但真实的NA是0.598 244。CAXCAD提供了一个控制真实数值孔径的操作数IMNA,可以直接控制像方NA。