




如从零开始制作苹果派,唯一的方法是自己创造新的宇宙。
——卡尔·萨根
(译者注:本章出现了大量晦涩的流体动力学的方程,对理解建模与模拟初学者理解溶出过程、文章和商业或学术软件中的溶出方程有一定的帮助。)
100多年前,人们就开始用Noyes–Whitney方程描述溶出现象了。从那时起,溶出科学已取得迅猛的发展。但该学科仍有许多尚未开发的领域,尽管流体动力学理论是溶出现象的基石,但药剂学教科书中一般只是做简单的论述。本章节将详细讨论流体动力学理论是如何影响溶出的。
扩散和对流将控制质量传递现象,从微观角度来看,扩散是随机漫步的过程,例如,将一滴墨滴入一杯水中,墨将在水中逐渐蔓延,见图3.1a。溶液需要经过很长一段时间才能达到均匀,药物溶出后的扩散也由同样的现象决定,见图3.1b。尽管,扩散是随机漫步过程,但分子总是从高浓度区域向低浓度区域移动,因此浓度梯度通常是扩散的驱动力,见图2.8。扩散动力学采用Fick’s扩散定律进行描述。另一方面,液体对流也会引起质量转移。通过搅拌,溶液将更快地获得均匀,流体的运动采用Navier–Stokes方程描述。
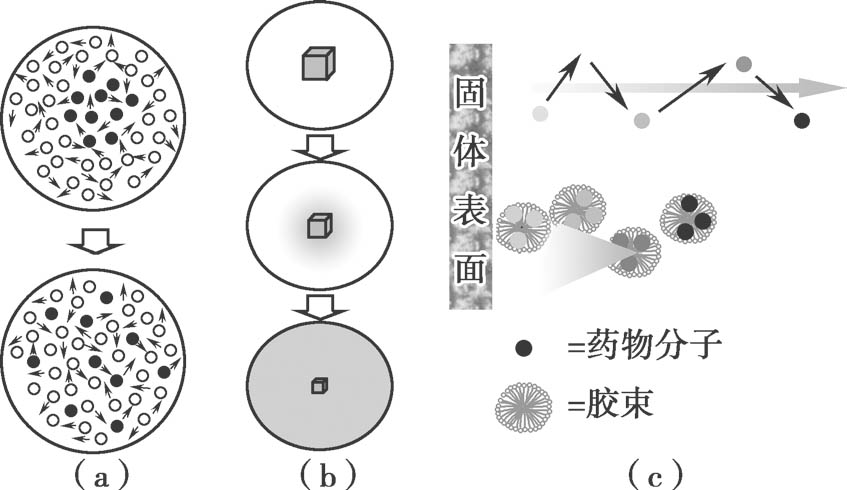
图3.1 药物扩散过程
(a)墨滴在水中的扩散;(b)药物在非搅拌条件下的溶出;(c)药物单体、胆汁胶束-药物结合物的扩散
传质方程由Fick’s扩散定律和Navier–Stokes方程衍生得到,Kohichi Asano写的《质量传递:基础与应用》一书中的第1章到第7章讲述了用这两个方程推导传质方程的过程。本章将讨论如何获得传质方程,以及它在生物药剂学建模中的应用;将先讨论扩散系数,接着讨论对流的过程。