




放射性核素的衰变总体上遵循负指数规律,但在衰变过程中,由于每个核素互不关联,故衰变是独立的随机事件。因此,不同时刻衰变的原子核数目不是一个固定的数值,总是围绕总体期望值上下波动,属于离散型随机变量,服从一定的概率分布。这就是核素衰变过程中的统计涨落特性,即放射性的统计性。放射性的统计性决定了放射性测量的统计误差不可避免,但可以通过提高测量计数、降低本底计数等方法加以控制。
绝对测量(absolute measurement)是指对样品放射性活度进行直接测量的方法,常用方法包括4π立体角法、固定立体角法、符合法和量热法。由于影响测量因素较多,主要用于标准源或校正源测量。相对测量(relative measurement),是指通过仪器测得的脉冲计数多少来反映样品放射性活度大小的测量方法,生物医学实验中,大多采用此方法比较样品间的差异。
衰变率是指单位时间内放射性核素的原子核发生衰变的次数,为放射性活度的物理量,常用每秒衰变数(disintegrations per second,dps)或每分衰变数(disintegrations per minute,dpm)表示。计数率是指放射性测量仪器在单位时间内所测得样品的脉冲数,为相对测量常用的物理量。常用每秒计数(counts per second,CPS)或每分计数(counts per minute,CPM)表示。测量效率是指仪器所测样品的计数率与样品的衰变率之比,是衡量测量仪器质量的重要指标,可用于对相对测量结果进行放射性活度的校正。
本底(background)是指仪器在无放射性样品的条件下所测得的脉冲记数,其主要来源有宇宙射线、环境辐射和仪器本身的电子噪声等。本底计数是衡量仪器质量的重要指标,要求越低越好。
放射性计数测量的统计误差是评价放射性测定值的离散范围或离散程度的物理量,分为标准误差(standard error)σ和相对误差(relative error)
δ
两类。标准误差是反映测量值与真值差别的指标,当样品的总计数为
N
时,根据Poisson 分布规律,其标准误差
 ,表示真值落在
,表示真值落在
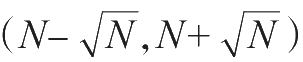 区间内的概率为63.3%,真值落在
区间内的概率为63.3%,真值落在
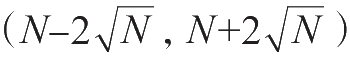 区间内的概率为95%。
区间内的概率为95%。
若计数
N
通过
t
时间获得,则计数率
n
=
N
/
t
,计数率的标准误差
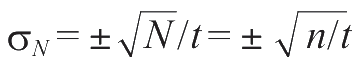 。当多次(
A
次)定时测量,每次计数分别为
N
1
,
N
2
,
N
3
……
N
i
,总计数
N
=∑
N
i
,平均计数
。当多次(
A
次)定时测量,每次计数分别为
N
1
,
N
2
,
N
3
……
N
i
,总计数
N
=∑
N
i
,平均计数
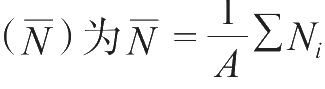 ,总计数为
,总计数为
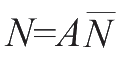 ,其平均计数
,其平均计数
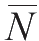 的标准误差
的标准误差
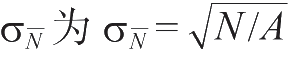 ,多次测量的计数率均值
,多次测量的计数率均值
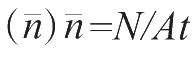 ,其标准误差为
,其标准误差为

相对误差是放射性标准误差与其测量值的百分比,用于鉴别和比较不同计数水平的误差大小。其计算方法即为标准误差除以测量值中的总计数。放射性测量一般要求相对误差控制在5%以内。
相对误差随测量计数
N
的增加而减小。对于计数率确定的样品S,可采用以下方法提高测量计数
N
:延长测量时间
t
,因为
N
=
nt
,故测量时间越长,计数越高;适当增加测量次数(
A
),由于标准误差
 和相对误差
和相对误差
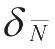 均与
A
的平方根成反比,因此,适当增加
A
可有效减少标准误差和相对误差;保持仪器处于最佳测量效率工作状态。放射活度一定的样品,其计数率随仪器测量效率提高而增加,相对误差越小。
均与
A
的平方根成反比,因此,适当增加
A
可有效减少标准误差和相对误差;保持仪器处于最佳测量效率工作状态。放射活度一定的样品,其计数率随仪器测量效率提高而增加,相对误差越小。
放射性样品测量计数(
N
)是核素衰变产生的计数(净计数)与本底计数之和。若样品计数水平过低,其测定值将明显受本底计数的影响。因此,本底计数决定了探测仪器的灵敏度。控制本底计数影响的方法有两方面,一方面是控制样品最小可测量活度,对于本底计数为
B
的探测仪器,其统计误差为
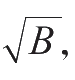 能分辨样品的最小可测量活度应大于
能分辨样品的最小可测量活度应大于
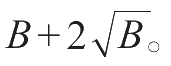 因此,在规定的时间(
t
)内,要将样品测量的相对误差(
δ
ns
)控制在一定范围内,其最小可测量活度为:
因此,在规定的时间(
t
)内,要将样品测量的相对误差(
δ
ns
)控制在一定范围内,其最小可测量活度为:
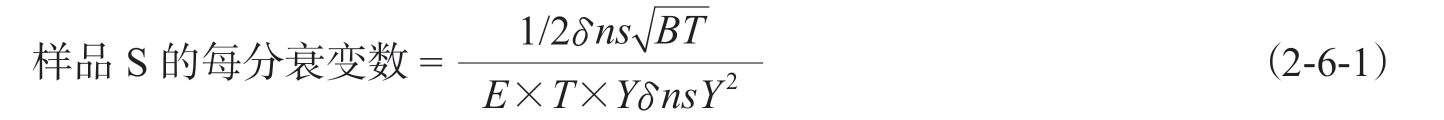
式中
E
为测量效率,
B
为本底。表明通过降低本底计数,提高系统探测效率,对于提高仪器的测量灵敏度极为重要。因此,目前常用品质因子(
Q
=
E
2
/
B
)来评价闪烁探测仪器的质量。另一方面,通过合理分配样品和本底的测量时间,也能够控制和减少低活度样品的放射性测量误差。合理安排测量时间有以下2 种方式:一种是在规定时间(
t
)内,分配样品测量时间(
t
s
)与本底测量时间(
t
b
),将
t
=
t
c
+
t
b
按
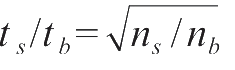 分配,所得测量误差最小。另一种是在限定的相对误差(
δ
ns
)范围内,合理分配样品测量时间(
t
s
)与本底测量时间(
t
b
)。若
n
b
/
n
s
<
δ
ns
时,
分配,所得测量误差最小。另一种是在限定的相对误差(
δ
ns
)范围内,合理分配样品测量时间(
t
s
)与本底测量时间(
t
b
)。若
n
b
/
n
s
<
δ
ns
时,

确定
t
c
后,根据
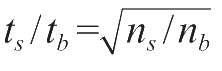 计算
t
b
。
计算
t
b
。
(兰晓莉)