




这一讲已经包罗了很多内容,在继续推进之前,让我们盘点一下已经做过的事情。我们的目标是把自旋和矢量空间结合起来。我们清楚了如何用矢量来代表自旋态,而且在这一过程中得以窥见态矢量所包含的信息(以及没有包含的信息)。下面简要地罗列了我们所做的工作:
· 基于自旋测量的知识,我们选择了3对相互正交的基底,它们分别被命名为
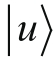 和
和
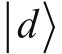 、
、
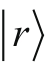 和
和
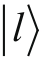 ,
,
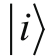 和
和
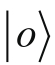 。因为基底矢量
。因为基底矢量
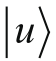 和
和
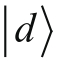 代表着物理上不同的态,所以我们可以断定它们彼此之间是正交的。换言之,
代表着物理上不同的态,所以我们可以断定它们彼此之间是正交的。换言之,
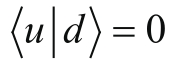 。这对
。这对
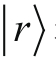 和
和
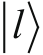 以及
以及
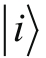 和
和
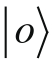 也都成立。
也都成立。
· 我们要使用两个独立的参数去定义自旋态,然后任意选择一对正交矢量作为基底,比如
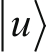 和
和
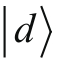 ,从而将所有自旋态都表示出来,虽然描述态矢量的两个复数需要有4个实数,我们依然选择全部表示出来。该如何处理呢?我们相当聪明,发现这4个实数并不完全独立
,从而将所有自旋态都表示出来,虽然描述态矢量的两个复数需要有4个实数,我们依然选择全部表示出来。该如何处理呢?我们相当聪明,发现这4个实数并不完全独立
 。归一化的限制(总概率为1)消除了一个独立的参数,相位无关性(态矢量的物理特性不会受到全局相因子的影响)又消除了一个。
。归一化的限制(总概率为1)消除了一个独立的参数,相位无关性(态矢量的物理特性不会受到全局相因子的影响)又消除了一个。
· 选定
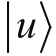 和
和
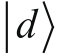 作为主要的基底,在额外的正交和概率基础的限制下,我们解决了另外两对基底如何用
作为主要的基底,在额外的正交和概率基础的限制下,我们解决了另外两对基底如何用
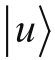 和
和
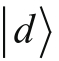 的线性组合来表示的问题。
的线性组合来表示的问题。
· 我们确认了使用列矢量来代表主要基底的方法,这种表示并不唯一。在第3讲中,我们将使用
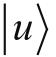 和
和
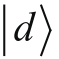 的列矢量去推导另外两个基底的列矢量。
的列矢量去推导另外两个基底的列矢量。
在得到这些具体结果的过程中,我们也顺便练习了态矢量的数学,并学到了这些数学对象是如何对应到物理自旋上的。尽管我们关注的是自旋,但其实同样的概念和技术也能应用到其他量子系统中去。在进入第3讲之前,请花一些时间去消化到目前为止的内容。正如我在本讲开始时说的,你真的会有所收获。