




接下来,我们来看
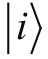 和
和
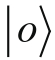 ,这个矢量代表自旋指向
y
轴方向,它需要满足如下条件:
,这个矢量代表自旋指向
y
轴方向,它需要满足如下条件:

这一条件说明入态(in)和出态(out)是正交矢量,就像上态和下态一样。在物理上这意味着如果自旋是入态,它就绝不会是出态。
对于矢量
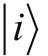 和
和
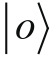 还有其他的限制,使用公式2-1和公式2-2表达的关系,以及我们实验的统计结果,可以写作:
还有其他的限制,使用公式2-1和公式2-2表达的关系,以及我们实验的统计结果,可以写作:
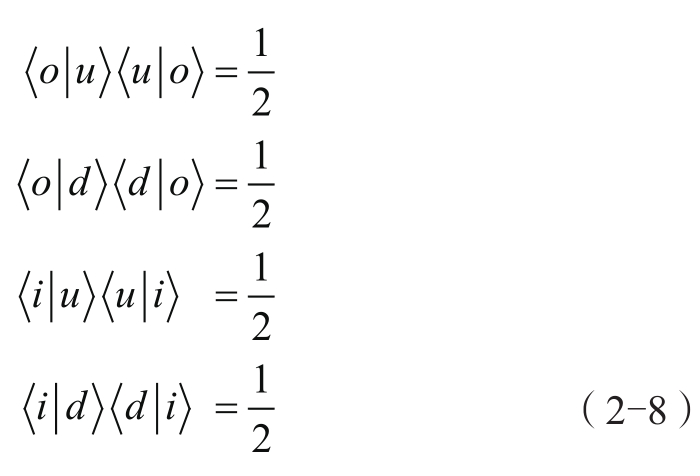
在前两个式子中,
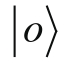 取代了公式2-1和公式2-2中
取代了公式2-1和公式2-2中
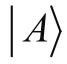 的位置。在后两个式子中,则用
的位置。在后两个式子中,则用
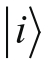 取代。这些条件说明,如果自旋指向
y
轴方向的话,指向
z
轴方向的测量会得出相等的向上或者向下的概率。同样,如果指向
x
轴方向去测量的话,得到向右或者向左的概率相同。这还要求:
取代。这些条件说明,如果自旋指向
y
轴方向的话,指向
z
轴方向的测量会得出相等的向上或者向下的概率。同样,如果指向
x
轴方向去测量的话,得到向右或者向左的概率相同。这还要求:
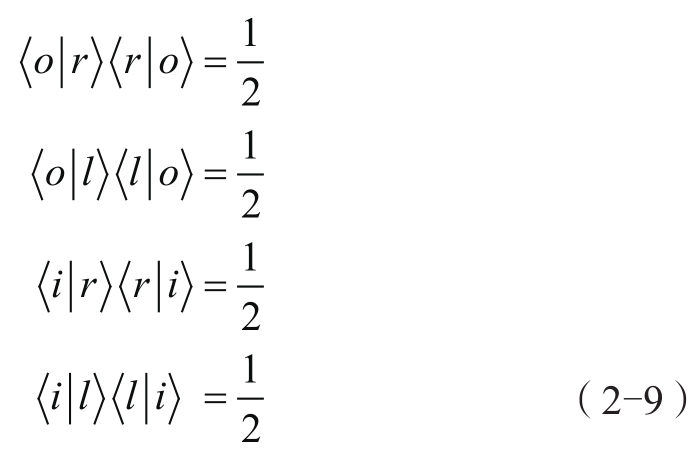
现在这些条件足够决定矢量
 和
和
 的形式了,不考虑相位任意性,结果如下:
的形式了,不考虑相位任意性,结果如下:
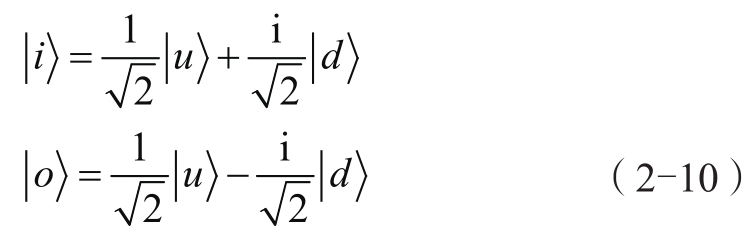
练习2-2:
证明
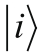 和
和
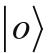 满足公式2-7至公式2-9中的所有条件,以及它们是不是唯一的。
满足公式2-7至公式2-9中的所有条件,以及它们是不是唯一的。
有趣的是,公式2-10中有两个分量是虚的。当然,我们所有的讨论一直都是在复数空间中进行的,但直到现在我们才真正在计算时用上了复数。公式2-10中的复数只是约定的还是必须的呢?给定自旋态的框架,复数就是必须的。证明过程有点乏味,但每一步都很直接,后边的练习题会给出一个大致步骤。使用复数是量子力学中普遍的特征,之后的内容中还会有更多的例子。
练习2-3:
暂时忘掉公式2-10中给出的
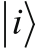 和
和
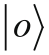 是如何用
是如何用
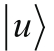 和
和
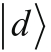 表示的,假设分量
α
、
β
、
γ
和
δ
都是未知的,则下式成立:
表示的,假设分量
α
、
β
、
γ
和
δ
都是未知的,则下式成立:
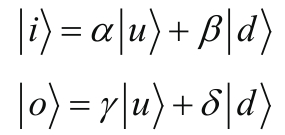
a)使用公式2-8验证
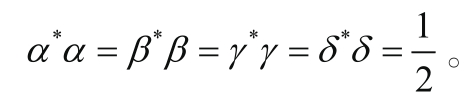
b)使用上面的结果和公式2-9验证
α * β + αβ * = γ * δ + γδ * =0。
c)证明 α * β 与 γ * δ 一定是纯虚数。如果 α * β 是纯虚数,则 α 和 β 不能都是实数, γ * δ 同理。