指向 x 轴方向

前面我们说过，我们能够把任意一个自旋态表示成基底 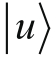和 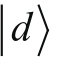的线性组合。现在我们尝试对矢量 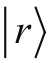和 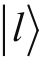做类似的处理，它们代表的是 x 轴的方向。先从 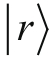开始。在第1讲的内容中，如果装置 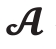初始制备出了一个态 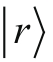，然后旋转去测量 σ _z ，测量结果一定是“向上”和“向下”的概率相等。所以 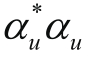和 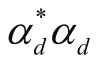都要等于1/2，满足这一点的矢量如下：

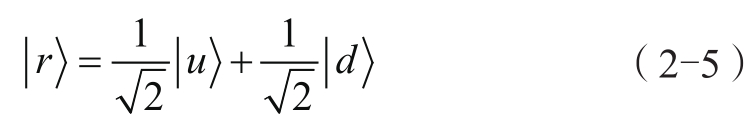
粗看起来，这样的选择有点任意，但后面我们能够看到，其中的任意性不会超过对 x 轴和 y 轴方向选择的任意性。

接着我们来看看矢量 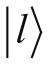。我们知道，当自旋被制备到向左时，测量结果显示， σ _z 向上和向下的概率依然是各为1/2。但这样还不够，还要有额外的条件来决定 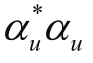和 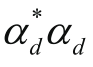的数值。前面我讲过为什么说 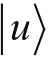和 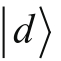是正交的，因为当自旋向上时，它绝对不会同时向下。而所谓向上和向下这个方向并没有什么特殊的，向左和向右也是如此。具体来说，如果自旋是向右的，那么测量到它向左的概率为0。用公式2-3类推可以得到：

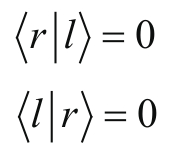
如此就能确定 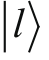的形式为：

Quantum Mechanics　量子力学练习

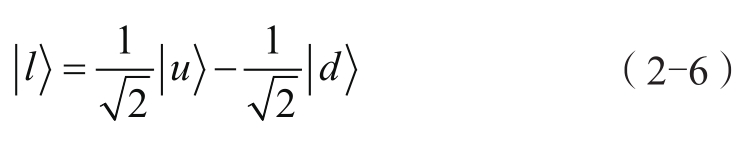
练习2-1： 证明公式2-5中矢量 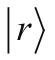与式2-6中的 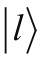正交。

我们对 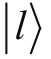的选择依然存不确定性，这叫作相位任意性（phase ambiguity）。假设在 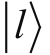上乘以一个任意的复数 z ，这不会影响到它和 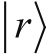的正交关系，但一般来说将破坏归一性（也就是模的长度为1）。但如果选择 z =e ^{i θ} （其中 θ 是任意实数），归一化就不会受到影响了，因为e ^{i θ} 本身具有单位长度，那么 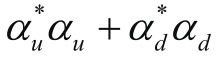依然等于1。由此，具有 z =e ^{i θ} 形式的复数被称为相因子，这种不确定性就叫作相位任意性。后面我们会发现，所有可以测量的物理量对全局的相因子都不敏感，所以我们在描述一个态的时候往往会忽略相因子。 HnBtSXzo35vWnrLHPqiYN8iqXDi3BgM3S4VGi1PylUwL60oF9JG2zwDHS0a9qrkq