




一位名叫山岸(Yamagishi)的教授在日本东京工业大学(Tokyo Institute of Technology)教两个班。他问早上上课的同学:“日本死于癌症、心脏病、谋杀和交通事故的人数比例是多少?”下面是早上上课的同学们给出的答案:
癌症:24%
心脏病:24%
谋杀:14%
交通事故:18%
他又向晚上上课的同学提出了相似的问题,但这次他没有提问百分比,而是问他们在1万起死亡事件中以下每个方面大约有多少起。下面是晚上上课的同学的答案:
癌症:1286(13%)
心脏病:1512(15%)
谋杀:487(5%)
交通事故:893(9%)
晚班的学生的估计大约是早班学生的一半。用百分比进行的估计与用其他方法进行的估计有什么区别吗?
研究表明,当我们基于概率做出决策时,我们倾向于关注分子而忽略分母。例如,大多数人(61%)更喜欢参与这样一种摸奖活动:有一个装有100个球的瓶子,其中9个是白球,摸出白球者即为获奖;而不是从10个球中只有1个是白球的瓶中摸出那个白球。9/100的概率被认为高于1/10的概率。如图5所示。
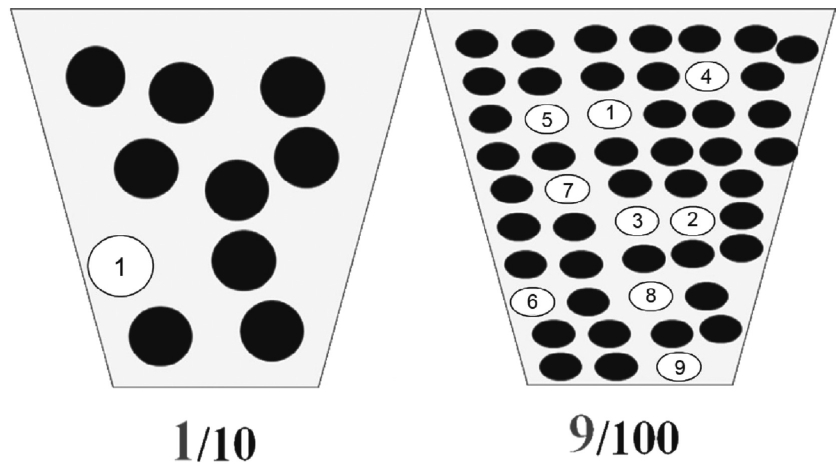
图5
这种现象被称为 比率偏差 (ratio bias),它也存在于受过高等教育以及在其领域有经验的人当中。
关于精神病学家被问及是否应该让某个精神病患者出院的问题,当个体攻击性行为的风险评估为100个此类患者中有20个时,大约40%的精神病医生反对释放,这意味着100个患有类似精神疾病的人中,大约有20个可能有攻击性行为。但只有20%的精神病医生反对释放风险评估为2/10的有攻击性行为的病人,换言之,10个有类似精神疾病的患者中有2个可能会有攻击性行为。而结果却是20/100看起来比2/10高。100个危险的精神病患者中有20个在街上游荡,看起来很多。而10个精神病患者中有2个在街上游荡似乎没那么危险。我在街上遇到他们中的一个的机会看起来很小。
当医生被要求评估一种医疗方案,其死亡率为每1000名患者中有176人死亡,他们会认为该方案的死亡率与100人中有37人死亡的方案相似。也就是说,17.6%等于37%。
研究者对陪审团也进行了类似的研究。他们被告知,某家商店发生了一起谋杀案,在这家商店发现的血迹与一名经常在那里购物的嫌疑人的DNA相吻合。1/3的陪审员被告知血液检测不可靠的概率是0.1%,另一组人被告知的概率是1/1000,而第三组人被告知的概率是2/2000。
表7展示了不同陪审团对犯罪现场发现的血液来源于嫌疑人的概率的估计。
表7
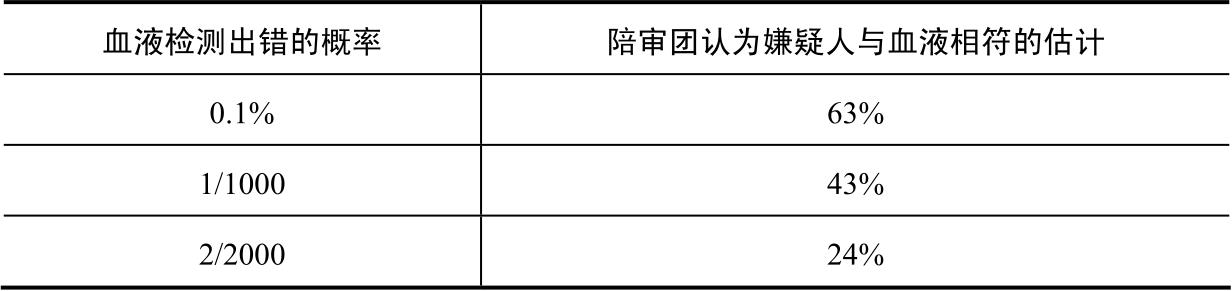
尽管上述三种不同的统计数字在数学上是相同的,但它们以非常不同的方式影响着陪审员。0.1%的概率似乎可以忽略不计。嫌疑人与犯罪现场的血迹不符的可能性是微乎其微的。当我们听到有1/1000的概率时,我们会想到可能是嫌疑犯的那一个人。但是当我们被告知概率是2/2000时,我们会考虑到有两个个体的测试可能是错误的。所以也许第二个就是凶手?
在上面提供的所有例子中,我们可以看到我们的注意力是如何更多地集中在分子上而不是分母上的。统计数据以不同的数学形式呈现,例如1%、1/100、2/200、10/1000或100/10000,这在我们的大脑中形成关于事件概率的不同感觉,尽管所有的值实际上在数学上是相同的。
总结
1.当我们听到用不同的数学形式提供的概率估计时,我们对它们的看法是不同的。
2.当概率以一个有分子和分母的简单分数的形式出现时,分子更能吸引我们的注意力。因此,为了做出明智的决定,我们应该仔细观察数字,把它转换成不同的数学形式,看看我们对风险评估或概率的最初感觉是否会改变。比如:如果有人告诉我们,不做手术就能康复的概率是1/10,在决定是否做手术之前,我们也应该把它看作是1000人中有100人在康复。如果我们对手术的看法前后一致,我们就应该坚持我们最初的决定。然而,如果概率表达方式的改变引起了我们前后不同的感受,我们便应该三思而后行。