




All the mechanical behavior involved in this study are performed in the Largescale Atomic/Molecular Massively Parallel Simulator (LAMMPS) [17] and employs a simulation time step of 0.01 ps. The model is visually analyzed using the Open Visualization Tool (OVITO) [18] . The embedded-atom method, which was developed by Daw and Baskes [19, 20] , is applied to govern the energetics and dynamics of Cu-Cu. The total potential energy E of a single atom i is calculated as follows:
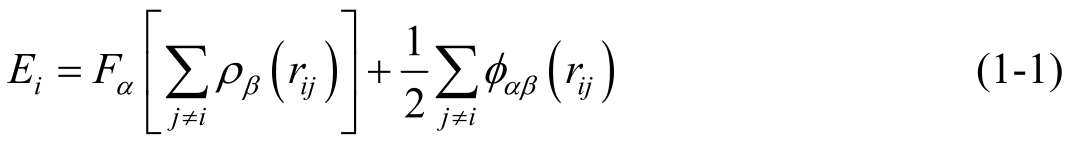
where F is the embedding energy, which is a function of the atomic electron density ρ ; ϕ is a pair potential interaction; α and β are the element types of i and j atoms. Both sums in the formula are over all neighbors of atom i within the cutoff distance.
In this work, a local part of the wire and corresponding local part of the substrate are developed to model the nanoindentation, contact, and separation of the wire and substrate [8] . The basic geometry of the Cu-Cu wire bonding model is shown in Fig. 1-1. There are two parts in the model: Cu wire and Cu substrate. The Cu wire consists of two different layers: a sliding layer and a Newton layer. The Cu substrate consists of three different layers: a sliding layer, a thermo layer, and a Newton layer. The Newton layers perform the contact behavior during the simulation. The sliding layers are used to provide the desired displacements. For the Cu wire, this layer is used to make the indenter move correctly. The thermo layer is used to control the temperature with the NVT ensemble (constant number of atoms, volume, and temperature) [21] . The initial temperature of the thermo layer is set at 0.1 K because the fluctuations of the atomic stress distributions due to the thermal effects can be significantly decreased [22] .
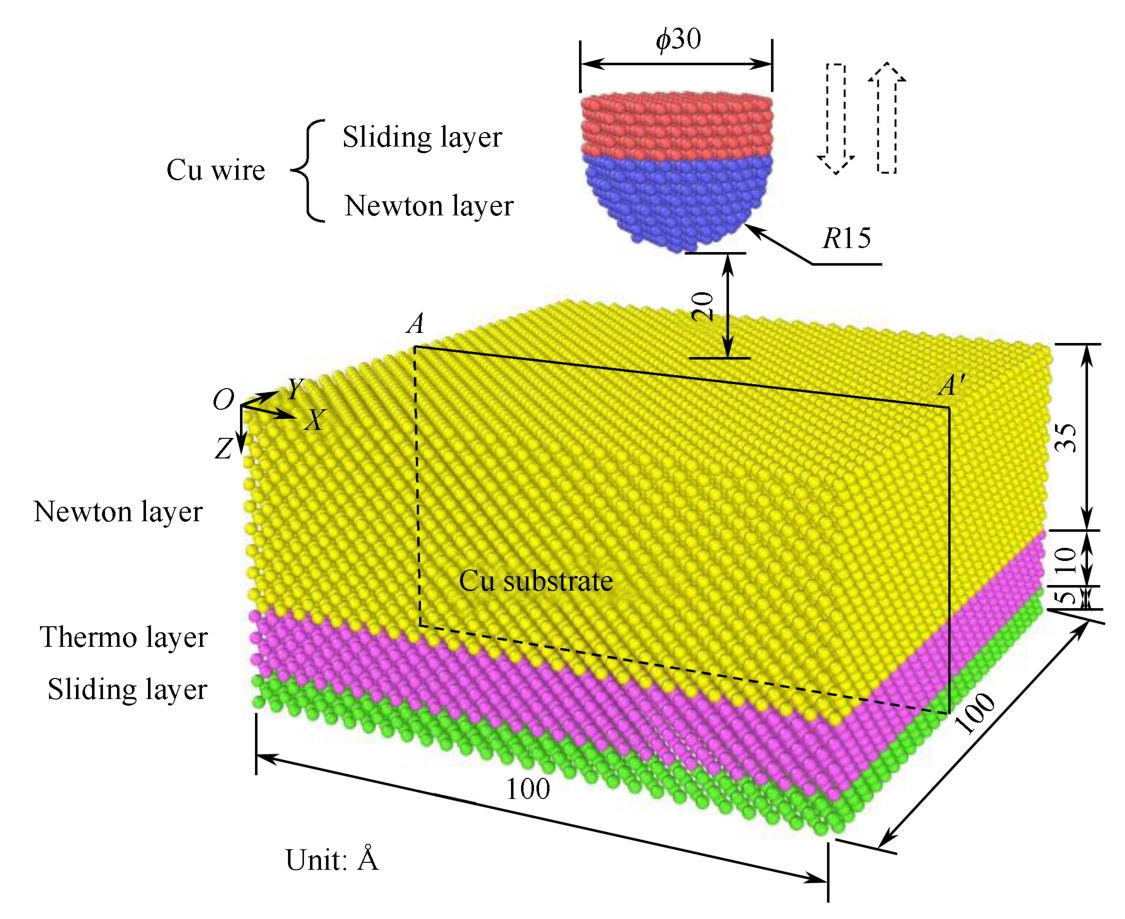
Fig. 1-1 The basic geometry of the Cu-Cu wire bonding model
According to previous studies [23,24] , the indentation speed of 10 m/s is used in this simulation. Prior to the indentation process, the system is allowed to have a relaxation of 100 ps to decrease its energy. The nanoindentation process consists of two steps: the loading and unloading processes. Firstly, during the loading process, a speed of 10 m/s is added to the Cu wire part (indenter) to move it along the negative direction of the Z direction towards the Cu substrate by 30 Å. Secondly, during the unloading process, the Cu wire part (indenter) is added at a speed of 10 m/s to move it along the positive direction of the Z direction and separate it from the Cu substrate by 30 Å. The loading force is calculated by summing the atomic forces of Newton layer atoms of the Cu wire part in the Z direction. The displacement of the indenter in the Z direction is taken as the abscissa of the load-depth curve. For the atomic stress analysis, the six components of the atomic stress tensor are calculated based on the spatial and temporal ensemble averages of the atomic virial stress [8,25] :
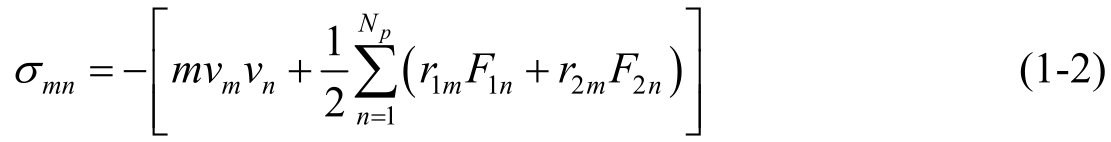
where
σ
mn
is the atomic stress component in the order of
m
,
n
(
x
,
y
, or
z
);
mv
m
v
n
is the kinetic energy contribution;
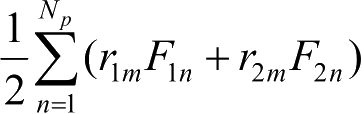 is the pairwise energy contribution, which is associated with the surrounding atoms from
n
=1 to
N
p
. Additionally, the von Mises stress is adopted to show the atomic stress distribution, as shown in Equation (1-3):
is the pairwise energy contribution, which is associated with the surrounding atoms from
n
=1 to
N
p
. Additionally, the von Mises stress is adopted to show the atomic stress distribution, as shown in Equation (1-3):
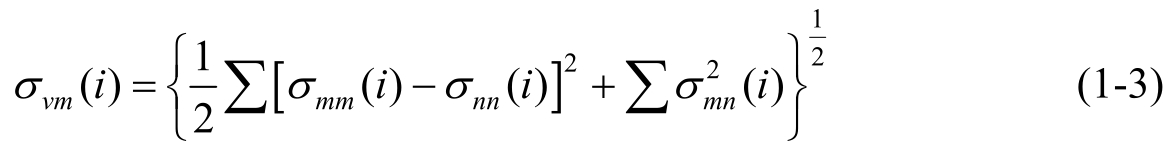
where σ vm ( i ) is the von Mises stress of atom i ; σ mn ( i ) is the atomic stress tensor in the order of m , n ( x , y , or z ).