




在我研究生生涯的最后一段时期,超弦理论风头正劲。爱德华·威滕(Edward Witten)是这个领域的天才,我认识的所有从事理论研究的研究生都在研读他最新的论文。英国理论物理学家保罗·狄拉克(Paul Dirac)对量子理论做出了奠基性贡献,和狄拉克一样,威滕也有着世界一流的数学能力。他获得过菲尔兹奖(Fields Medal),还拥有和爱因斯坦一样的物理直觉。当你刚刚自认为抓住了他一篇论文的要点时,他可能又发表了一篇新的颠覆性的论文——这个理论已经经历了两次革命,第三次革命马上就要到来了。我们不得不逼迫自己努力跟上他的步伐,因为弦理论实在太令人兴奋了。它虽然在理论上是简单的,但在数学的推演上却极为复杂,为新的创造性理念留出了巨大的想象空间。
乍看上去,弦理论似乎是反直觉的。在经典物理学中,一根真实的、正在振动的弦会产生整数频率的驻波。不断靠近弦,观察它的细节,你会发现它其实是由原子构成的。根据弦理论,如果你不断靠近一个基本粒子,观察它的细节,那么你会发现它是一根由能量构成的振动弦。在弦的世界里,弦才是最基本的元素。当你离它们够远时,它们才表现得像粒子。弦理论比量子场论更具音乐性,对此,加来道雄(Michio Kaku)曾做过精妙的描述:“我们在自然界中看到的亚原子粒子、夸克和电子不是别的,正是一根小小的振动弦奏出的音符……物理学就是你可以给出的关于振动弦的和谐定律……宇宙则是由诸多振动弦共同演奏的一首交响乐。” 1
那么,爱因斯坦在他人生的最后30年里慷慨激昂地写下的“上帝的思想”,又是什么呢?现在,历史上首次出现了一个“上帝的思想”的参选者,它就是宇宙之声。
基于弦理论的音乐本质,以及通过对音乐和声音的理解,我能仅凭直觉就迅速地掌握这个理论。此外,它还与我把物理学和音乐结合起来的期望高度契合。如果弦调好了,那就开始演奏吧!基本弦不同的振动方式可以产生不同的音符,这些音符可以转变成不同的粒子性质,譬如电荷、质量和自旋。此外,弦的特定振动方式能产生量子化的引力场,也即引力子(graviton)。至此,我们终于得以把引力引入量子物理。和爱因斯坦一样,许多顶尖的物理学家都曾试图将量子力学与引力统一起来,但他们都失败了。现在,一根简单的振动弦就优美地做到了这一点。
在“振动弦的物理学能给出所有传递作用力的粒子,以及所有基本粒子”的意义上,弦理论很自然地成了万物至理。不过,这种优美是有代价的。当弦理论学家开始探索弦的物理学原理时,他们获得了一些惊人的发现。在小空间中运动的弦与在大空间中运动的弦遵循同一种物理学,我们把这种性质称为T对偶(T-duality)。在弦理论的假设中,我们不是生活在四维空间,而是十维空间。即便在今天,强大的粒子对撞机和多种多样的太空实验仍在寻找这些隐藏的额外维。然而,在如今这个丰富的统一新世界里,似乎并不存在弦理论的唯一解。实际上,弦理论共有5种不同的版本。
在我研究生生涯的最后一年里,布兰登伯格召开了一场组会。20世纪80年代早期,一些理论家致力于推动应用量子场论解决早期宇宙问题,他就是其中之一。在组会上,布兰登伯格告诉我们,他认为弦理论已经发展成熟,可以用来解决一些关于早期宇宙的问题了。我还记得他当时说:“如果我们能通过弦理论找到暴胀理论的机制或者其替代理论,那就再好不过了。”对我来说,在接下来的几年里,我要做的事情已经很清楚了:深入学习弦理论,以探究宇宙暴胀到底是不是一个弦理论现象。
在离开布朗大学之前,我走进弦理论学家安托·杰维奇(Antal Jevicki)的办公室,然后关上门,问他:“杰维奇先生,我想在博士后阶段研究弦理论,您能给我一些建议吗?”杰维奇带着他匈牙利式的笑容,说:“整装待发,开始行动。”这场竞赛的获胜者将得到一份博士后研究员职位的合同,以及永久教职。作为一名博士后,你必须进行独立的研究,并在自己的研究领域取得一定的成就。在理论物理学领域,若想获得教职,必须做过博士后的工作。然而,很多科学家在获得永久教职之前都要经历10年炼狱般的博士后研究员生涯。这些研究职位的竞争极为激烈,而在顶尖的学术机构得到一份博士后研究员职位的机会更是渺茫。不久之后,我发现,在申请伦敦帝国理工学院博士后的300多名候选人中,只有两人最终得到了这份职位。由于我在研究生阶段的最后一年里独立完成的一些工作,我成了幸运儿之一。
因此,我最终还是离开了布兰登伯格,跨过大西洋,来到了伦敦帝国理工学院——欧洲理论物理学的圣地之一。那时,我天真地以为,在物理学领域,布兰登伯格和库珀推崇的“他山之石”与“即兴演奏方法”很普遍。然而,帝国理工学院却截然不同。作为一个新入职的博士后研究员,对失败和被轻视的恐惧在我的潜意识里慢慢滋生。与其他的博士后交流对我并没有什么帮助,尤其是我的舍友尤西·卡克基纳(Jussi Kalkkinen)。卡克基纳是一位优秀而刻苦的芬兰弦理论学家,他能把自己锁在办公室里进行马拉松一般的冗长计算,演算那些十一维的超引力方程。我曾尝试效仿他,但在两个小时的计算之后,我就坐在办公室里昏昏欲睡了。
当开始思考一名成功的博士后必须具备的能力时,我不禁怀疑,这个似乎主要是“闭上嘴,动笔算” 2 的领域是否真的适合我。很快我就感到有点力不从心了,因为其他博士后所掌握的技术与数学能力都比那时的我更强。所以,在理论研究中,什么才是最重要的呢?是技术,还是直觉?现在回想起来,当时困扰着我的是学界正在争辩的问题,即什么是理论物理研究中的“美”,而这是我在课堂上无法学到的东西。
史蒂文·温伯格(Steven Weinberg)是诺贝尔奖获得者、电-弱核力统一理论的先驱,在《终极理论之梦》( Dreams of a Final Theory ) 3 一书中,他提到了狄拉克的一次演讲:
1974年,狄拉克来到哈佛大学,讲述他作为现代量子电动力学的奠基者之一的历史性工作。在演讲快结束时,他向我们研究生致辞,并建议我们关注方程的美,而不是意义。虽然对学生而言这并不是一个好建议,但在狄拉克的工作中,甚至在物理学的大部分历史中,对物理学中的美的追求始终是一个重要的主题。
我们可以理解温伯格部分同意狄拉克的说法的原因。温伯格曾应用纤维丛理论——一个有着极为优美的几何公式的理论,发现了电磁力与弱力实际上是一种统一的力,即电-弱力。他认为,学生不必严格遵循有关“不要回头去关注那些方程的意义”的建议。如果温伯格没有回头去追问他研究的那些方程和所做的计算的意义,那么他就不会获得突破性的发现,也就不可能因此获得诺贝尔奖。原来,温伯格将自己的方程用在了错误的物理学系统(强核力)中。他在诺贝尔奖获奖致辞中说:“1967年秋天的某日,在驾车去麻省理工学院的路上,我突然意识到,我把正确的方程用在了错误的问题上……根据对称性自发破缺(Spontaneous Symmetry Breaking,简称SBB) 4 的理论,弱力与电磁力可以被统一。”
那么,狄拉克所说的物理学中的“数学之美”到底是什么呢?许多物理学家认为,物理学之美是指它看起来有多优美。在词典中查阅“优美”(elegant)一词时,你会发现诸如“精练”(refined)、“高雅”(tasteful)、“雅致”(graceful)、“高级”(superior)等词汇。当一个方程简明扼要、直击本质时,我们就便认为它精练。当一个方程由数字、字母和符号等数学语言构成时,我们就说它高雅。当一个方程具有推导出其他方程的能力时,我们就觉得它高级。一个优美的方程是非常美丽的。
在物理学中,关于优美的一个绝佳例子是描述行星运动的方程。开普勒总结了三条极为精确的定律,可以用来解释行星绕太阳进行的椭圆运动。然而,其中缺少一个关键因素,即引力。于是,牛顿出现了。牛顿的万有引力定律表明,开普勒三定律可以由一个方程推导而来。相似地,在爱因斯坦证明了时间与空间可以统一成四维时空后,另一系列极为精确的方程,即描述电磁现象的麦克斯韦方程组,也可以从一个“母”方程推导而来。这些统一振奋了人心,因为它们简化了方程。
在随后的几年里,人们发现,大多数粒子都有与之对应的反粒子,这个发现催生了现今物理学中最重大的理论之一——弦理论。弦理论的目标是建立一个框架,以容纳自然界中四种已知的基本作用力,它因此被称为“万物至理”。弦理论并不是唯一试图实现这种统一的理论,它虽然来源于基础粒子物理,但是基于狄拉克发现的粒子对称性,它尚未被实验证实。不过,弦理论的成功却凸显了人类对物理学之美的认识所面临的挑战。
具有数学之美的理论是非常迷人的,因为它为研究人员提供了一个舞台,他们可以在这个舞台上探索能够反映真实物理世界的虚拟现实场景。弦理论的优美不仅体现在统一量子力学与引力的目的上,还体现在具体的实现手段上。正所谓“千里之行,始于足下”,从一维振动弦的方程出发,我们可以推导出所有作用力(引力、电磁力、弱力和强力)的方程。此外,弦理论还有一个我认为非常美丽的特征。通过额外维(我们所处的四维时空之外的维度)的几何形状,弦理论为4种基本作用力和物质的存在提供了一种极为有趣的描述。
一个物理学理论无论多么优美,它都必须符合事实,而争论往往会围绕着一个理论做出的不符合预期的预言来展开。为了理论的自洽,充满对称之美的弦理论需要依靠额外维,有人据此认为弦理论预言了一个无限世界的存在。关于这一点,我们将在后面的章节中进行讨论。由于无限世界远远超出了我们的观测能力,也超出了大多数物理学家的常识范围,所以一些物理学家认为弦理论并不优美。尽管如此,这种追求对称性与数学之美的审美倾向,一直影响着现代物理学的发展进程。
作为一个年轻的物理学工作者,我对狄拉克与温伯格的天分以及两人对物理学的贡献无比崇敬,同时也将他们的建议铭记于心。然而,狄拉克为我指引的方向与我博士后工作需要面对的现实,以及我期望能在新的工作环境和同事交好的愿望相悖。总之,在离开了我在普罗维登斯的耗费6年时间建立的交际网后,我必须在帝国理工学院与其他博士后同事建立新的友谊和社交关系。我还记得在亨利·庞加莱研究所(Institut Henri Poincaré)参加一场理论物理研讨会时,一群博士后同事争论着一个弦理论问题,我则在他们周围晃来晃去。我兴奋地试图从一个思辨的角度切入话题,但其他博士后却继续相互讨论,仿佛我不存在一般。这给我上了一课:若想加入他们的讨论,我就必须拿出自己的真本事。你的方程呢?要想在这个球场上打球,我必须学会各种动作——这意味着我要进行一些数学方面的训练。这一切让我回想起了我参加过的爵士乐聚会,在那些聚会上,每个人的关注点都在于谁能完美地“演奏”出和弦的变化。
狄拉克想表达的意思非常清楚:“工欲善其事,必先利其器”,闭上嘴,动笔算,你终将在这个领域取得成功。因此,我打算收起天马行空般的即兴演奏和类比思维,并尝试狄拉克的方法,看看从这些方程中能获得什么样的物理学发现——优美的数学到底预言了什么现实。我并不是一个人在战斗,实际上,我大部分同事都严格地遵循着这种狄拉克式的科研方法。博士后们紧闭房门,趴在桌上夜以继日地工作。我们在计算上花费了大量的时间,希望能解开一个通向颠覆性发现的谜题,或者至少得到一篇值得发表的论文。
我经常端着双倍浓缩咖啡走进办公室,继续计算超引力。在我博士后生涯的几年里,宇宙学研究的主要目标遵循着布兰登伯格所指示的方向,即找到早期宇宙中物理学运作机制之间的深层联系,以解释宇宙中的大尺度结构是如何演化而来的。科学家认为超引力就是这种理论,尤其是它的十一维版本,这个版本被称为十一维超引力。超引力有可能就是狄拉克梦想中的理论,因为它非常优美,仅一行方程就将曾经分离的引力方程和电-弱统一理论结合起来,后者是温伯格关于电-弱力的理论。大家都认为,沿着十一维超引力深入探索,就能找到更多隐藏着的具有简洁美的数学公式。当时我正在寻找超引力微观世界的一种隐藏形式,它关乎宇宙中的大尺度结构的形成。
超引力其实是爱因斯坦的广义相对论的一个版本,只不过它披着超对称的外衣。超对称把费米子与玻色子联系在一起,并把每个玻色子与费米子配对成“超对称粒子”。玻色子是传递作用力的粒子,比如传递电磁力的光子。而费米子既是构成物质的粒子(比如电子和夸克),又是这些亚原子粒子的反粒子。只要照照镜子,你就能明白超对称的运作机制了。由于你的身体是左右对称的,所以即便镜子把你的左半身与右半身颠倒了,镜中的你与他人眼中的你仍是相似的。在不影响物理系统行为的前提下,超对称就像一面镜子,把玻色子与费米子对调了。
从理论上讲,超引力不仅令人着迷,而且意义深远,不过我却被计算本身深深吸引,那些符号自带美感的同时,又共同呈现出震撼的视觉效果。那一刻,我的敬畏之情油然而生,时间仿佛回到了20年前,我又变成了那个站在自然博物馆里盯着爱因斯坦写下的符号的小男孩。只需提高或者降低某个变量的值,我的笔尖就可以操纵虚拟的几何世界。如果能得到一个偶然的发现,付出再多的努力似乎也是值得的。大量的项会相互抵消,方程因此变得更简单,纸上的方程和我的思维也瞬间变得更清晰了。有些时候,某个方程的形式会出乎预料地与某个已知的宇宙事实相对应,而我知道,在这种狄拉克式的努力之下,这些方程终将指向我们的宇宙。虽然偶尔能获得巨大的满足感,但这终究是一项艰苦的工作。在工作间隙,博士后们会边喝咖啡边抱怨自己的徒劳努力,有时也会兴奋地分享自己的“神恩时刻”,或者只是想喝点咖啡,以便让大脑满载着能量继续做计算。
我的目标是熟练掌握超引力,那种操纵方程的感觉总是让我感到很愉悦。时光飞逝,转眼之间,两年博士后时光马上就要结束了。在探究超引力和超弦理论如何揭示宇宙结构的秘密方面,我觉得自己并没有取得进展。虽然我在超引力计算上遇到了困难,但其他人似乎都在发表揭示超级世界中隐藏的数学结构的精彩论文。即便我很努力,但我还是陷入了自我怀疑的深渊。也许布兰登伯格和库珀会为有意阻止我进入数学的迷宫而感到抱歉,因为只有精通数学,我才能掌握在研究中取得进展所必需的技能。
一天下午,在一次休息时间过后,我收到了理论组行政人员格拉济耶拉(Graziela)的一封电子邮件。邮件中说,理论组的组长克里斯·艾沙姆(Chris Isham)博士想和我谈谈。我被吓到了,心想:“他终于发现了,我就是个骗子。”我丢下正在进行的计算,慢慢地站起来,朝艾沙姆的办公室走去。一路上我都在嘀咕,他会不会把我看作小丑,并要求我离开他那声誉卓著的研究小组。
我第一次知道艾沙姆是在霍金的《时间简史》一书中,他是与罗杰·彭罗斯(Roger Penrose)一同出现的。艾沙姆、彭罗斯和霍金是同事,他们都是世界级的数学物理学家。艾沙姆身上笼罩着一层神秘的光环,并集合了独立、创造性的思维和超人类的数学能力,魅力十足。他在量子引力理论方面取得了关键性的突破,而量子引力理论试图统一量子力学与引力,也即“万物至理”。在20世纪60年代,艾沙姆是一位年轻的奇才,也是诺贝尔奖获得者阿卜杜勒·萨拉姆(Abdus Salam)的博士生。萨拉姆的突出贡献是提出了关于两种基本作用力的大统一理论,但这两种力不包括引力。
与霍金一样,艾沙姆也患有一种罕见的神经系统疾病,这使得他在一生中的大部分时间里都要承受难以忍受的痛苦。他非常高,在帝国理工学院的长廊里,你可以越过如潮水般涌出教室的学生,远远地看到他。他走起路来一瘸一拐的,身体微微斜向一方,有点儿像舞台剧中演员的动作。他在许多方面都令人钦佩,比如他很爱笑,风趣而幽默,经常提出建设性意见。一个帝国理工学院的学生与我分享了一个关于艾沙姆的故事。
在一个潮湿的冬日清晨,伦敦阴沉的天气让你一点儿也不想起床时,艾沙姆的举动却震惊了昏昏欲睡的学生,让他们亢奋起来。他突然宣布,要把推导了一半的公式倒着推回去。“这只是一个惯例而已。如果你能从右往左读,那为什么还要坚持从左往右读呢?”他狡黠一笑,如此问道。学生们从震惊中回过神来,也不再浪费时间做笔记了,都专注地看着他倒推公式。那天的课程内容是关于纤维丛的,那是艾沙姆当时最喜欢的课题之一。他总是能在课堂上深入浅出地讲解纤维丛。他身体里的每个细胞都装着数学,所以无论它朝向哪个方向——无论是朝前还是朝后、朝上还是朝下,对他来说都无所谓。
我走进艾沙姆博士宽敞的办公室,看到他正坐在一张倾斜着的扶手椅上休息,双脚翘在桌子上。他的双臂微微颤抖着,身后的黑板上写满了对拓扑理论(关于拓扑空间规则的极为复杂的代数操作)的说明。这些内容极多,一张A4纸是写不下的。看到我时,他微微一笑,也不浪费时间,直截了当地切入正题。“你为什么要来这里?”他问。我有些紧张地回答:“我想成为一位优秀的物理学家。”艾沙姆接下来的话令我惊讶不已:“那就别再读那些物理书了。你需要培养你的直觉,因为它是伟大的理论物理学家的灵感源泉。”仿佛他的科研能力还不够令人印象深刻一般,接着,他平静而认真地告诉我,他曾在梦中训练自己的大脑进行冗长的计算。那时的我还不知道他在对待精神和哲学方面的问题时态度非常认真。在告诉了我他的秘密之后,他又问我:“你有什么爱好?”他在睡梦中(我只在晚上睡觉)施展的技艺让我目瞪口呆,我神思恍惚地答道:“我会在晚上演奏爵士乐。”他沉默了一会儿,才道:“你应该多多演奏音乐。我也唱歌,我发现音乐对激起直觉而言是一项很理想的活动。”说到这里,他停顿了一下。“看到这些书了吗?”他指着分析心理学创始人卡尔·荣格(Carl Jung)的著作全集问,“15年来,我一直在学习荣格学派的精神分析学。你可以看看第九卷第二部分《伊雍:自性现象学研究》( Aion: Researches into the Phenomenology of the Self )。物理学研究自有其神秘的一面。你知道沃尔夫冈·泡利(Wolfgang Pauli)与荣格共事过吗?”
我并不知道,所以感到很吃惊。作为量子力学的奠基人之一,泡利被爱因斯坦亲自提名诺贝尔奖。泡利能迅速发现数学错误,且无法容忍毫无条理的理论,他的名言是:“你的理论连错误都算不上。”他是狄拉克的忠实拥护者,且预言了一种难以捉摸的粒子——中微子的存在,而中微子被认为是一种不可忽视的技术力。我很难相信,泡利竟然会与心理学扯上关系,但我的想法很快就发生了转变。艾沙姆指着另一本书《从原子到原始型》( From Atom to Archetype ),那是泡利与荣格在20年间的书信集。“书中提到,泡利从出现在梦中的一个符号得到启发,提出了泡利自旋矩阵。你想把这本书借去看看吗?”我不仅借走了那本书,还视它为珍宝,因为我刚刚获得了深刻的领悟。这是一个有待开发的新领域。我不再和理论组的同事一起在工作间隙喝着咖啡抱怨冗繁的计算,而是在波多贝罗路(Portobello Road)上的一家酒吧里一边小酌,一边阅读那些书信。
凭借艾沙姆给我的特权,我每星期都能与他讨论理论物理中的基本问题,我像他的弟子一般遵循着他的指示。我加入了一支爵士三重奏乐队,并在诺丁山(Notting Hill)的剧场里做了两场演出。我阅读了荣格的著作,并且告诉了艾沙姆我的想法。几个月后,我的新爱好就收到了成效。当时,我在一个项目上卡了很久。我试图把弦理论与宇宙膨胀联系在一起,也即宇宙在诞生后经历了一个快速膨胀(或暴胀)的阶段这一理念。一天晚上,我来了段萨克斯独奏,演奏曲目是约翰·柯川的《PC先生》( Mr . PC )。中场休息时,我的脑海中出现了一幅图像,我知道它一定有助于解决我在项目中遇到的问题。第二天,我带着这个新发现醒来,匆匆跑到办公桌前,草草写下一些方程。这些方程与一个叫非对易几何(noncommutative geometry)的数学分支相关,而后者提出,早期宇宙中的光速是可变的。我与宇宙学家若昂·马盖若(Joäo Magueijo)就这种新联系共同发表了一篇文章,后来这篇文章被引用了100多次。这虽然并没有让我离自己的超引力宇宙结构之梦更近一步,却证明了艾沙姆的方法对我来说是有用的。
在艾沙姆与布兰登伯格对我演奏音乐的鼓励之下,以及出于对他们追求数学的卓越与优雅的敬佩,我的狄拉克方法开始发生变化。与方程“共舞”变成了一个多层次的任务。在学习爵士乐的过程中,练习音阶和技术固然很重要,但走出去并与他人合奏也十分重要。即兴演奏是一种即时行为,练习它的唯一方式就是去公开场合演奏。我慢慢意识到,我在科研过程中忽略了这一点。我对狄拉克方法的理解太流于表面了。通过把我研究的问题和面对的挑战带入爵士乐演奏中,我发现自己就像一个正在玩沙盒游戏的小孩,丝毫不担心有没有犯错,或是显得傻不傻。在多年保有对物理学与音乐的热爱,却一直把它们限制在两个不同的领域之后,突然之间,音乐就激发出了我的数学直觉。我第一次发现,直觉也是一条通向新发现的大道。最终,泡利与荣格的交流使得泡利发现了物质的新性质和自然的新法则。自从进入大学以来,将音乐与宇宙学结合起来的想法就一直萦绕在我脑海里,而现在,我把它们从我的直觉中挖掘出来,直面它们,我发现它们并没有我想象中那么古怪。
与他人一起演奏音乐成为我科学实践的一部分,它也是一种研究方法,而且非常有趣。在夏日纽约的通宵爵士乐晚会上,我会随时进行物理计算。每到中场休息时间,当爵士乐迷们热烈地讨论音乐时,我会提到我的物理学研究,并且把它们与爵士乐联系起来。我采用的依旧是狄拉克方法,只是换了个环境而已。在这些音乐会上,我找到了一种做研究的新形式,我也因此变得玩心十足。我凝视着小号手与爵士乐独奏手换场,就像在看两个超对称粒子进行超对称反演。我永远不会忘记我曾告诉一位现在很有名的钢琴家他的演奏是几何的。一位次中音演奏者加入了我们的讨论,他说:“虽然我听不懂你在说什么,但他的演奏真美!”
这里面有一个关键的几何概念,即等距,也就是一个点集中的任意两点之间的距离保持恒定不变。我所谓的钢琴独奏是“几何的”的一个简单例子,类似于在二维平面上取一个正方形,并滑动它。这个滑动的正方形与原来的正方形是等距的,因为四条边上任意两点之间的距离保持不变。而有些曲面是弯曲的,那么在这种曲面上移动正方形,即使再怎么做也无法保持它的四边之间的距离不变。通常,一位爵士乐独奏者会重复一段有旋律与节奏的组合,或是反复演奏即兴段,并且在全部12个调上演奏它——在旋律组合的音符之间,组合在不同调上的变换不会改变音符之间的距离。
几年之后我发现,当年在斯莫斯时,我试图在几何推理、对称性和音乐之间建立联系的想法并不疯狂。值得一提的是,在音乐和即兴演奏中,对称性与几何推理功能的使用有着惊人的相似之处。我们来看看史提夫·汪达(Stevie Wonder)的《你是我生命中的阳光》( You Are the Sunshine of My Life ),以及德彪西(Debussy)的《帆》( Voiles )。这两首歌曲都展现了人类的共同情感中一些强有力的东西,当然,音乐本身也很美妙。两首歌曲都使用了对称的音阶,之所以这么说,是因为当你把它们画出来时,它们看起来是对称的。想象一下把12个音符写在圆周里:如果我们从C音开始,按顺序逐次向上走半步,持续12次,我们就又回到了C音。这就是12个音符的几何表示(一个其上分布着离散点的圆周)。
我们可以用线把这些音符连在一起。等边三角形是二维三边图形中对称性最高的,正六边形是二维六边图形中对称性最高的。在图4-1中,六边形上的音符为C音、D音、E音、升F音、降A音和降B音,它们共同组成了一个被称为“全音音阶”的对称音阶。它听起来像什么呢?你可以在《你是我生命中的阳光》的开头听到它,在歌唱部分开始之前,电子键盘会演奏出一些欢快的上行音符。在德彪西的《帆》中,全音音阶则是下行的。

图4-1 全音音阶的六边形对称性
我们可以创造诸如减音阶(一个正方形)等其他对称音阶。派特·马蒂诺(Pat Martino)是当今最伟大的爵士乐吉他手之一,他于1980年患上了致命的脑动脉瘤。手术拯救了他的生命,却让他患上了失忆症,他不得不重新开始学习吉他。巧合的是,他开发了一套基于两种“亲本类型”对称性的新系统,它们与吉他指板的几何结构天生相合。这些亲本类型或者说和弦仅仅是对称的增三和弦与减七和弦。马蒂诺做过许多演示,展示了母和弦生成一系列次级和弦的力量。
与之类似的是,柯川也使用对称音阶作为他的专辑《巨人的步伐》的基础,关于这一点,我们很快就会进行详细讨论。柯川告诉戴维·阿姆兰(David Amran),他的一个关于音乐的简单理念是受到爱因斯坦关于相对论的著作的启发,这个理念就是对称性。我研究了柯川的曼荼罗,发现它具有强烈的对称性。基于惯性参考系之间的时空对称性,爱因斯坦提出了狭义相对论和四维形式的电动力学。此外,他还利用卷曲时空的对称性,证明了加速观察者与静止观察者之间的等价性。在统一且简化的对称性理念的基础上,爱因斯坦才得以成功表述那些复杂的、截然不同的物理学理念。
我曾有幸与马蒂诺交谈,他是一个慈祥的人,言语之间带着缜密的逻辑。他告诉我,他希望找到一个能迅速地执行他的即兴演奏理念和技术的系统。我露出了会心的微笑。“很多物理学家都渴望找到一种能解释众多现象的最有效的理论。”我说。马蒂诺和柯川都受教于已故的费城爵士乐吉他手丹尼斯·萨多拉(Dennis Sandole),萨多拉把对称音阶称为“八度音阶与三度音阶之间的等分” 5 ,并将这个概念传授给了马蒂诺和柯川。然而,柯川和马蒂诺并没有意识到,对称音阶及其对称性破缺与物理学之间存在着深层联系。从对称音阶的对称性破缺中,我们可以一窥物理学的对称性破缺。
和弦往往涉及一个主音。例如,由音符C、E和G构成的C大调和弦,其主音为C。如果你演奏这个和弦,那么C音就将是你听到的最明显的音符,而G音与E音将会起到为C音增添和声并润色的作用。不过,对称和弦有多个主音,所以它听起来非常模糊,那些音符均匀地展开,并且归入不同的音调。例如,C全音和弦的5个音调:C音、D音、E音、升F音、降A音和降B音都是它的主音。由于存在这种不确定性,所以对称音阶在音乐中扮演着极为特殊的角色。几百年来,诸如拉威尔和巴赫等作曲家都用它来制造张力或矛盾感,通常出现在和弦转换的乐段。减音阶也是一种很常见的对称音阶,广泛存在于爵士乐,以及乔治·格什温(George Gershwin)和科尔·波特的作品中,它能创造两个具有主音的和弦之间的移动。
在图4-2中,左图展示了对称减音阶,右图展示了主音阶。如果你仔细观察,就会发现只要改变4个音符中的2个,减音阶就可以变成主音阶。在对称音阶中,不同的主音之间并没有层级之分。相比之下,非对称主音阶破坏了对称性,而且产生了层级,这就导致了主音的出现,也即大调和弦,其重要性高于音阶中的所有音符。早期宇宙中的非对称性就是通过类似的机制使早期宇宙结构产生层级的,我们在后面的章节中讨论这一点时,会回到这个重要的音乐类比上来。
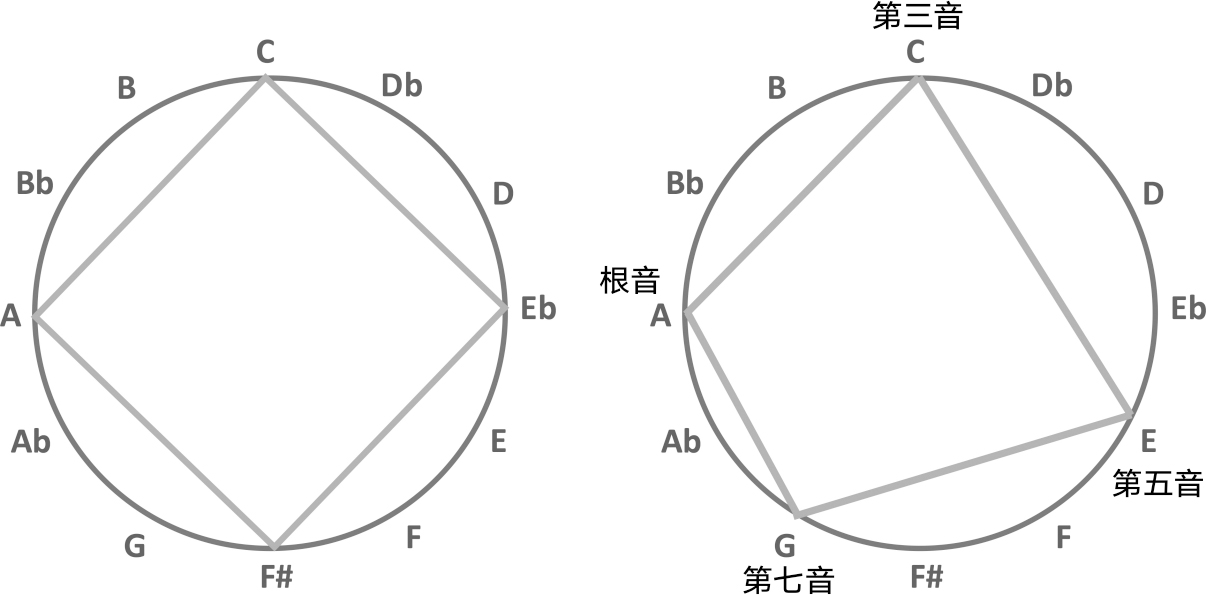
图4-2 对称减音阶(左图)与主音阶(右图)的对称性破缺示例
在我读博士、做博士后,接着成为独立开展研究的教授的那些年里,爵士乐音乐家待在音乐学院里,花了上千个小时的时间来学习音乐理论和乐器。和其他物理学家在一起时,我通常会藏起自己对物理学与音乐之间的联系的好奇。然而,这并没有动摇我的信念。毕竟,狄拉克方法认为,数学(尤其是对称性的应用)促进了基础物理学的发展,而我则在斯莫斯的音乐晚会上亲身体验了音乐中的几何结构和对称性。此外,当我进行次中音独奏时,我的脑海中经常会闪现物理上的灵感火花。几年后,我欣慰地发现,那些致力于寻找美的人推动了物理学的形成,他们在音乐和数学的结合中发现了美,后人称他们为毕达哥拉斯学派。看上去,我已经远远落后于毕达哥拉斯学派了。