




既然我们知道质数有无穷多个,那么不妨问问自己:有没有什么简单的办法能将所有质数按照顺序一个不漏地列出来呢?古希腊哲学家、数学家埃拉托斯特尼首次提出了解决这个问题的办法,我们称之为“筛选法”。你只需要写下所有整数:1,2,3,4……然后筛出2的所有倍数,再筛出3和5的所有倍数,以此类推,继续筛出所有质数的倍数。埃拉托斯特尼筛选100以内所有质数的示意图请见图1,这些数字共有26个。利用这种简单的筛选法,我们已经列出了10亿以内的质数表。
要是能列出一个公式来自动寻找所有质数(而且只有质数),那岂不是更快、更简单?然而数学家琢磨了十几个世纪,依然没有找到这样的公式。1640年,法国著名数学家费马提出了一个公式,他认为用这个式子算出的结果都是质数。
费马的公式是这样的:
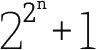 ,其中n代表自然数,例如1、2、3、4等等。
,其中n代表自然数,例如1、2、3、4等等。
利用这个公式,我们可以得出如下结果:
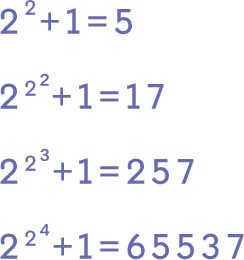
事实上,这几个数的确都是质数。不过大约一个世纪以后,德国数学家欧拉却发现,按照费马的公式得出的第五个数(
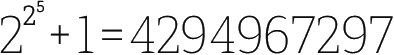 )不是质数,事实上,这个数等于6700417和641的乘积,费马计算质数的经验公式也因此被证伪了。
)不是质数,事实上,这个数等于6700417和641的乘积,费马计算质数的经验公式也因此被证伪了。
另一个能够算出大量质数的重要公式如下:
n 2 -n+41
这个公式中的n同样是自然数。我们将1到40的自然数代入这个公式,得到的结果都是质数,但不幸的是,这个式子走到第41步的时候栽了个跟头。
事实上,
41 2 -41+41=41 2 =41×41
这是一个平方数,不是质数。
我们再介绍一个试图寻找质数的公式:
n 2 -79n+1601
这个质数公式适用于79以内的自然数,但被80打败了!
所以我们直到现在都没能列出一个只能算出质数的通用公式。
数论中还有一个既没被证明也没被证伪的有趣问题,人称“哥德巴赫猜想”。这个猜想是在1742年被提出的,它宣称任何一个偶数都能表示为两个质数之和。不用费多少力气你就会发现,对于一些简单的数字,这个猜想完全成立,比如说,12=7+5,24=17+7,32=29+3。然而数学家耗费了无数心血,却依然无法完全证实这个猜想,与此同时,他们也找不出任何一个反例。1931年,苏联数学家施尼雷尔曼朝验证哥德巴赫猜想的目标迈出了建设性的一步。他证明了任何一个偶数都能表示为不多于300000个质数之和。30万个质数和2个质数之间的确存在巨大的鸿沟,另一位苏联数学家维诺格拉多夫又将证明的结果进一步推进到了“4个质数之和”。但是,维格拉多夫的“4个质数”离哥德巴赫的“2个质数”还有最后的两步,看来这两步才最难走,要最终证明或证伪这个难题,谁也说不清到底需要多少年或者多少个世纪。
如此说来,要得出一个能够自动推出任意大质数的公式,我们距离这个目标似乎还很遥远,确切地说,我们甚至无法确定这样的公式是否存在。
所以现在,我们或许可以转而思考另一个谦逊一点的问题:在某个给定的数字区间内,质数所占的百分比是多少?随着数字的增大,这个百分比是否大致保持恒定?如果不是的话,那么它是上升还是下降?为了回答这个问题,我们不妨试着数一数质数表中的数字。通过这种方式,我们发现100以下的质数共有26个,1000以下的质数有168个,1000000以下的有78498个,1000000000以下的有50847478个。我们可以将相应区间内的质数个数列成下表:
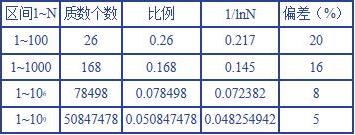
根据这张表格,首先我们可以看出,随着整数越来越多,质数在所有数字中所占的比例越来越小,但并不存在所谓的最大质数。
数字越大,质数出现的频率就越低,我们能不能用一个简单的数学式来表达这样的趋势呢?答案是肯定的,描述质数平均分布的定理是整个数学领域最重要的发现之一,它可以简单地表达为:从1到大于1的任意自然数N的区间内,质数所占的百分比约等于N的自然对数的倒数。N越大,这个式子得出的结果就越精确。
你可以在上页这张表格的第四列找到N的自然对数。比较一下第三列和第四列的数字,你会发现二者的确十分相近,而且N越大,两列数字的偏差就越小。
和数论领域的其他很多命题一样,质数定理最初是在实践中被发现的,而且在很长一段时间里,我们并没有找到任何可以支持它的严格的数学证据。直到19世纪末,法国数学家阿达马和比利时数学家德拉瓦莱·普森才终于成功地证明了这一定理,不过他们采用的方法过于繁难,我们在此暂且略过。