




你大概还记得课本上的几何学,根据你的记忆,这是一门度量空间的科学,它的主要内容是一大堆定理,分别描述各种各样的距离和角度的数值关系(比如说著名的毕达哥拉斯定理,它描述的就是直角三角形边长的数值关系);但事实上,要研究空间最基本的特性,很多时候你根本不必测量任何长度和角度。几何学的这个分支被称为位相几何学或者拓扑学,它是数学中最困难也最刺激的一个部分。
我们不妨举一个简单的例子,看看典型的拓扑问题是什么样子。请设想一个封闭的几何面,比如说一个球,球面上的线条将它分割成了多个区域;要画出这样的图形,我们可以在球面上选择任意多个点,然后用不相交的线将这些点连接起来。接下来我们要问,初始点的数量、划分相邻区域的线的数量和区域的数量之间有何关系?
首先我们可以清晰地看到,如果把这个球压扁,比如说变成南瓜的形状,或者拉伸变成黄瓜,球面上点、线和区域的数量都将保持不变,和原来的完美球面一模一样。事实上,同样的命题适用于任意形状的封闭面,这就像一个气球,无论你怎么挤压、拉伸、扭转,只要别把它切开或者撕碎,它的形状都不会影响我们的推想和问题的答案。拓扑几何的这一特性和以数值关系为主(譬如长度、面积和体积之类的关系)的普通几何学很不一样。事实上,如果我们将立方体拉伸成平行六面体,或者将球体压成煎饼,它的各项数值必然发生巨大的变化。
对于这个划分成若干区域的球,我们可以将它的每个区域分别压平,于是球变成了多面体,不同区域之间的边线也变成了多面体的棱线,初始的那些点现在是多面体的顶点。
于是,我们最初的问题也就顺理成章地变成了本质上完全相同的另一个问题:任意形状的多面体顶点、棱和面的数量之间有何关系?
我们在图3中画出了五个正多面体(每个面所拥有的棱和顶点数量完全相同的多面体)和一个随心所欲的不规则多面体。
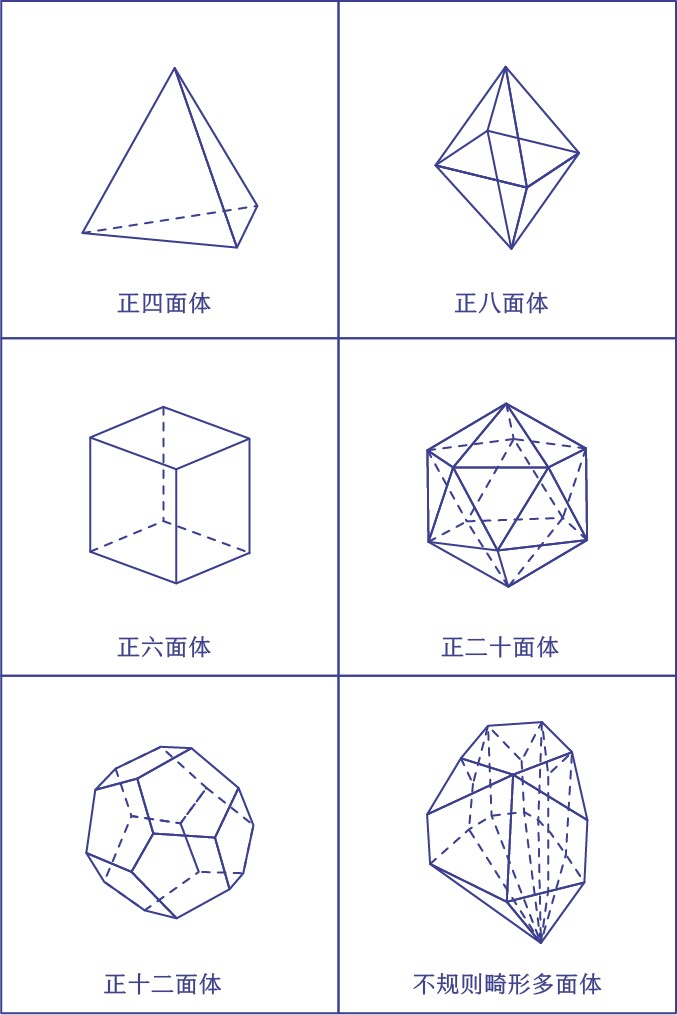
图3
我们可以数出每个几何体顶点、棱和面的数量,看看这三个数字之间有何关系。
亲手数过之后,我们画出了下面这张表格。
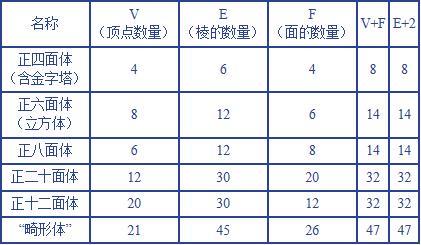
首先,前三列数字(V、E和F)之间似乎没有任何关系,但只要稍加研究你就会发现,V和F两列数字之和总是等于E加2。因此,我们可以写出三者之间的数学关系:
V+F=E+2
这个等式是只适用于图3中的五种多面体,还是适用于任意多面体?你可以试着画几个不同于图3的其他多面体,再数一数它们的顶点、棱和面,然后你会发现,上述等式适用于任何情况。那么显然,V+F=E+2是拓扑学中的一个通用数学定理,因为这个等式不需要测量棱的长度或者面的大小,它只和几个不同的几何单元(即顶点、棱和面)的数量有关。
我们刚才发现的多面体顶点、棱和面之间的数量关系是由17世纪的法国著名数学家勒内·笛卡尔首先注意到的,后来另一位数学天才莱昂哈德·欧拉严格证明了这个定理,因此它被称为“多面体欧拉定理”。欧拉的公式还证明了一个有趣的推论:正多面体只可能有五种,也就是图3中的那五个。