




根据前述,分子光谱分析是基于光与物质分子作用时,分子发生了量子化的能级跃迁,测量由此产生的吸收或发射的光谱的波长和强度等而进行分析的方法。本节简要概述常见分子光谱分析方法:紫外可见分光光度法(比色/显色法)、红外光谱法、拉曼光谱法、分子荧光光谱法与分子磷光光谱法,并结合研究经历,重点介绍基于小分子光学(显色﹑荧光/磷光)探针的分子光谱分析(包括核酸荧光探针和纳米光学探针)方面的一些新研究进展。
紫外可见分光光度法是典型的吸收光谱法,在190~800 nm波长内测定物质的吸光度等,其可用于各种物质的鉴别、检测以及定量测定研究。检测仪器为紫外可见分光光度计。
由表2-1可知,分子的紫外可见吸收光谱是由价电子能级跃迁产生的。通常电子能级间隔为1~20 eV,这一能量恰好落于紫外与可见光区(200~800 nm)。每一个电子能级之间的跃迁,都伴随分子的振动和转动能级的变化,因此,电子跃迁的吸收线就变成了内含分子振动和转动精细结构的较宽的谱带。
紫外可见光谱主要反映了分子中某些基团的信息。有机化合物分子中与紫外可见吸收光谱有关的价电子有三种:形成单键的σ电子、形成双键的π电子和分子中未成键的孤对电子(n电子)。当分子吸收一定能量的光时,这些电子就会跃迁到较高的能级,此时电子所占的轨道称为反键轨道。有机化合物最主要的电子跃迁类型有以下3种:(1)成键轨道与反键轨道之间的跃迁(即σ→σ * ,π→π * );(2)非键电子激发到反键轨道(即n→σ * ,n→π * ),其中各种跃迁所需能量大小为σ→σ * >n→σ * >π→π * >n→π * ;(3)电荷迁移跃迁,即在光能激发下,导致电荷从化合物的一部分迁移至另一部分。金属配合物的主要电子跃迁类型有以下3种:(1)配位体围绕的金属离子d-d电子跃迁和f-f电子跃迁;(2)配合物的电荷迁移跃迁(包括:配位体→金属的电荷转移;金属→配位体的电荷转移;金属→金属间的电荷转移);(3)金属离子微扰的配位体内电子跃迁。图2-2为常见电子跃迁所处的波长范围及强度 [7] 。饱和碳氢化合物的σ→σ * 跃迁一般发生在真空紫外区,而在近紫外无吸收。例如,乙烷的最大吸收波长在135 nm。
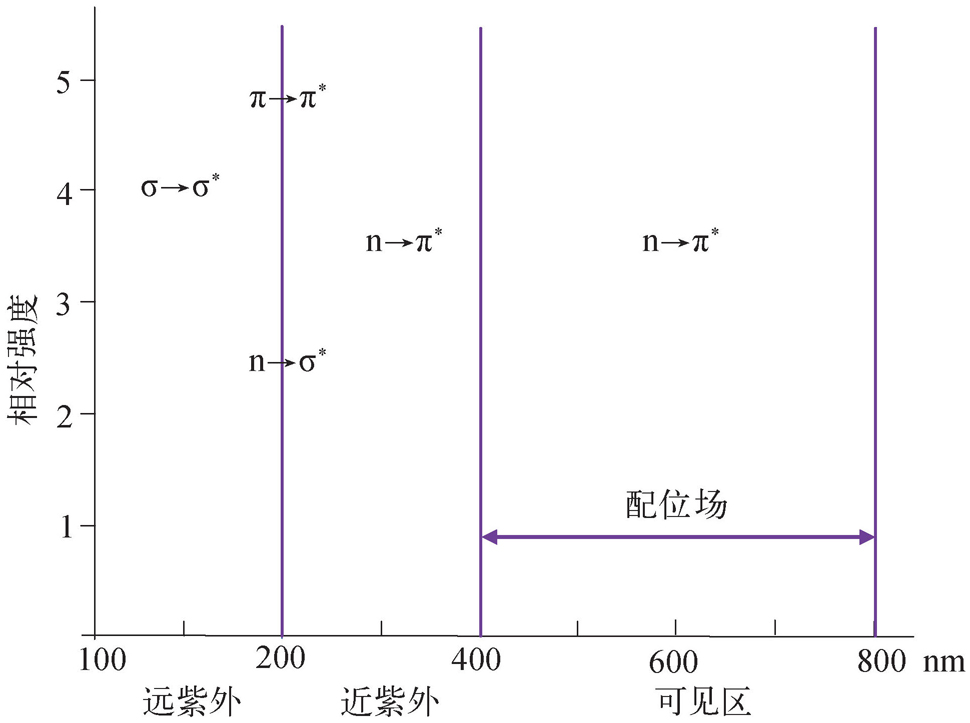
图2-2 常见电子跃迁所处的波长范围及强度
紫外可见吸收光谱的定性分析主要通过吸收波长的位置与强度进行,其定量分析则是基于朗伯-比尔(Lambert-Beer)定律:
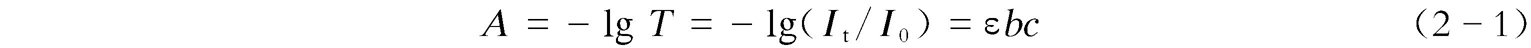
式中, A 为吸光度; T 为透射率; I t 为透射光强度; I 0 为入射光强度; b 为光程,cm; c 为分析物浓度,mol/L;ɛ为摩尔吸光系数,L/(mol·cm),与物质的性质、入射光波长、温度、溶剂等因素有关。朗伯-比尔定律表明:当一束单色光通过含有吸光物质的溶液后,溶液的吸光度与吸光物质的浓度及溶液的厚度成正比。在同一波长处,溶液中不同组分的吸收行为互不相干,且吸光度具有加和性。在吸收光谱法中,光源、样品、检测器一般在同一直线上。通常,吸光度在0.2~0.8时测量较为准确;吸收光谱法重复性好、准确度高,相对误差为2%~5%,较适用于微量物质的定量测定(微摩尔浓度水平)以及标准方法的制定 [2] 。图2-3是甲酚紫染料及其衍生物的紫外可见吸收光谱图。
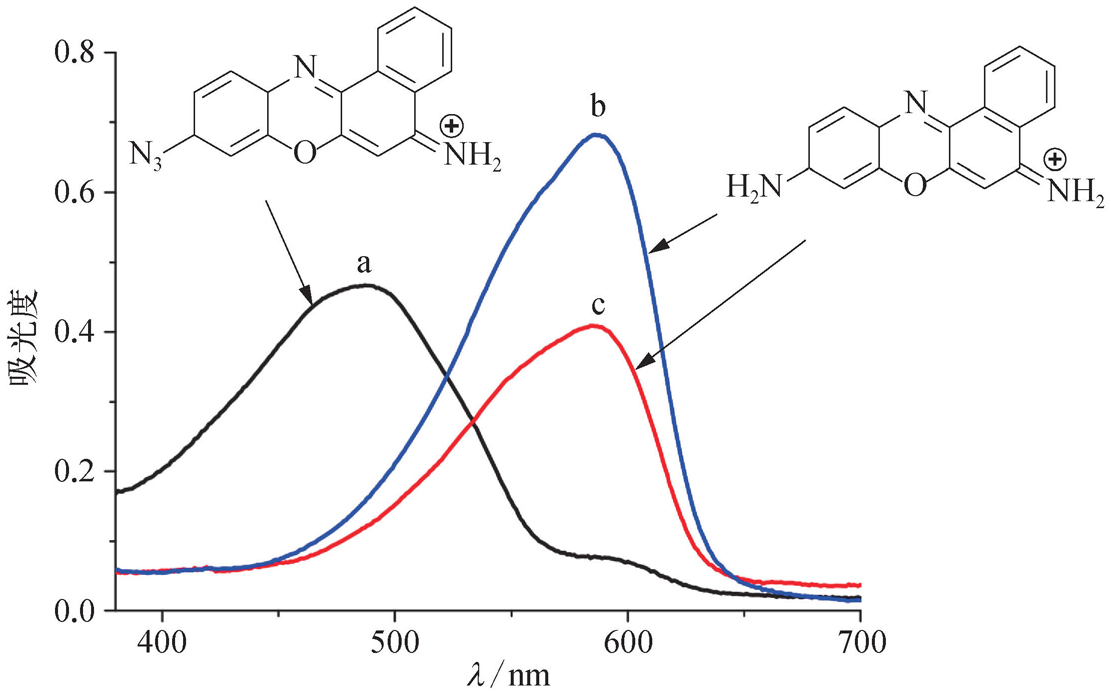
图2-3 甲酚紫染料及其衍生物的紫外可见吸收光谱图 [8]
曲线a:叠氮化的甲酚紫(25μmol/L)吸收光谱(最大吸收波长 λ max =488 nm);曲线b和c:浓度分别为25μmol/L和15μmol/L的甲酚紫吸收光谱(最大吸收波长 λ max =588 nm)。介质均为60 mmol/L的磷酸盐缓冲溶液(pH=7.4)
待测物本身在紫外可见光区没有强吸收,或在紫外光区虽有吸收但为了避免干扰或提高灵敏度,可加入适当的显色剂,使反应产物的最大吸收移至可见光区,这种测定方法称为比色法。将待测组分转变成有色化合物的反应叫显色反应,与待测组分形成有色化合物的试剂称为显色剂或比色探针。显色剂一般分为无机显色剂和有机显色剂两大类。常用的无机显色剂有硫氰酸盐、钼酸盐、过氧化氢、卤素离子等。有机显色剂的种类和数量繁多,在反应的灵敏性和选择性方面一般优于无机显色剂,常见的有机显色剂有偶氮类、三氮烯类、苯基荧光酮类、卟啉类、环状低聚物类、水溶性高分子类等。
显色试剂在20世纪一直是分子光谱分析的前沿领域,其发展为各种金属离子的快速检测提供了有效的手段。例如,偶氮胂Ⅰ可用于稀土元素、钙等检测;高分子显色剂壳聚糖缩7-(对甲酰基苯偶氮)-8-羟基喹啉-5-磺酸、聚乙烯醇缩3-(对甲酰基苯偶氮)-4,5-二羟基-2,7-萘二磺酸、聚2-丙烯胺缩5-(对甲酰基苯偶氮)-8-氨基喹啉可用于不同样品中铁、镁与铜 [9,10] 的测定等。
红外光谱法又称红外分光光度分析法,是分子吸收光谱的一种,主要应用于分子结构的表征与分析。由于各个物质的含量也将反映在红外吸收光谱上,可根据峰位置、吸收强度进行定量分析。
红外光的辐射能量为1.7 eV~1.24 meV,此辐射不足以引起分子中电子能级的跃迁,但可以被分子吸收,从而引起振动和转动能级的跃迁。在红外光谱区实际所测得的谱图是分子的振动运动与转动运动的加和表现,故红外光谱亦称为振转光谱。按红外光波长不同,往往将红外吸收光谱划分为三个区域(表2-1)。红外光谱主要用红外光谱仪进行分析,有些傅里叶变换红外光谱仪可实现近红外、中红外及远红外等多种分析模式。
在 n 个原子组成的分子中,非线性分子具有3 n -6种基本振动状态,而线性分子则有3 n -5种。在振动过程中,虽然不改变极性分子中正负电荷的电荷量,却改变正负电荷中心间的距离,导致分子偶极矩的变化。分子中不同的振动状态与不同的振动频率相对应,因而形成不同的振动能级。能级间的能量差与红外光子的能量相当。当一束连续波长的红外光透过极性分子时,某一波长的红外光的频率若与分子中某一基团的振动频率相同,即发生共振。这时,光子的能量通过分子偶极矩的变化传递给分子,导致分子对这一频率的光子的吸收,从振动基态激发到振动激发态,产生振动能级的跃迁。因此物质分子吸收红外光发生振动和转动能级跃迁,必须满足以下两个条件:(1)红外辐射光具有的能量等于分子振动能级的能量差Δ E ;(2)分子振动时必须伴随偶极矩的变化(具有偶极矩变化的分子振动是红外活性振动,否则为非红外活性振动)。例如,对称原子组成的分子H 2 、O 2 、N 2 等振动不会改变偶极矩,自然也就不会产生红外吸收,对这类分子进行分析时,使用拉曼光谱分析会更有效。
红外吸收光谱多用透过率
T
(%)与波数
σ
表示(图2-4)。双原子分子振动频率
ν
(Hz)的计算公式为
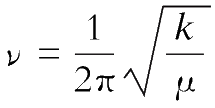 。用波数
σ
(cm
-1
)作单位时,即
。用波数
σ
(cm
-1
)作单位时,即
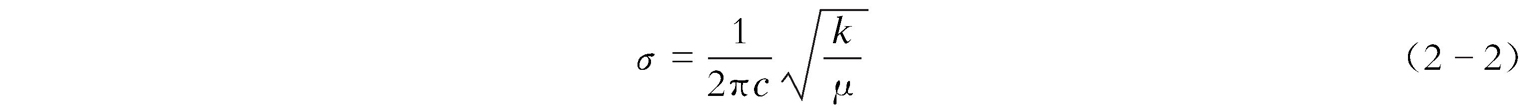
式中,
k
为化学键力常数,dyn/cm;
μ
为折合质量,g,
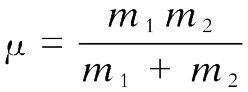 ,其中
m
1
、
m
2
分别为两原子质量;
c
为光速。若化学键力常数
k
单位使用N·cm
-1
,折合质量μ采用原子质量单位
m
=1.65×10
-24
g,则上式可简化为
,其中
m
1
、
m
2
分别为两原子质量;
c
为光速。若化学键力常数
k
单位使用N·cm
-1
,折合质量μ采用原子质量单位
m
=1.65×10
-24
g,则上式可简化为
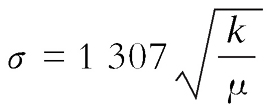 。
。
现在红外光谱法所沿用的有关分子结构与特征频率的规律,不是通过数学模型计算导出的,而是在大量实验数据的基础上加以归纳和总结出来的。目前有大量的标准红外光谱图(如Sadtler标准红外光谱集)可供查阅。红外光谱法的主要特点是特征性强、测定速度快、不破坏试样、样品用量少、操作简便、分析灵敏度较高,能分析各种状态的试样;然而,该方法对样品的纯度要求高(>98%),且定量分析误差较大。关于红外光谱的详细解析在此不作详述,仅附部分官能团的特征频率供参考(表2-3) [3] 。图2-4为己酸的红外光谱图,实际化合物解析时需要考虑诱导效应、共轭效应和偶极场效应等内部因素的影响,同时还需要考虑溶剂、测试条件等外部因素的影响。
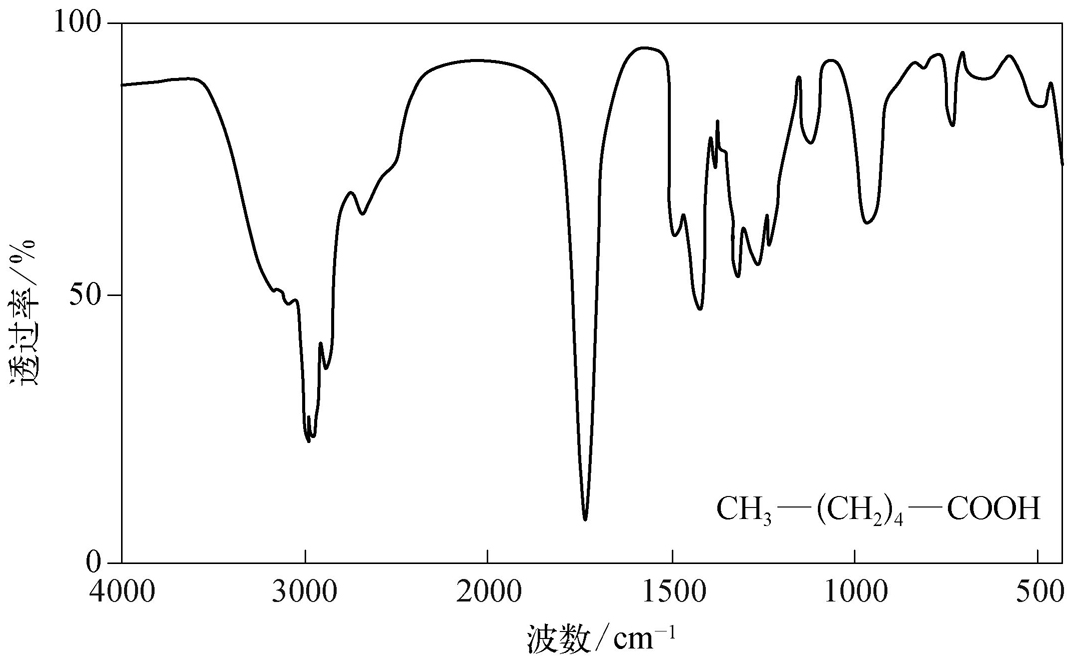
图2-4 典型的红外光谱图(己酸)
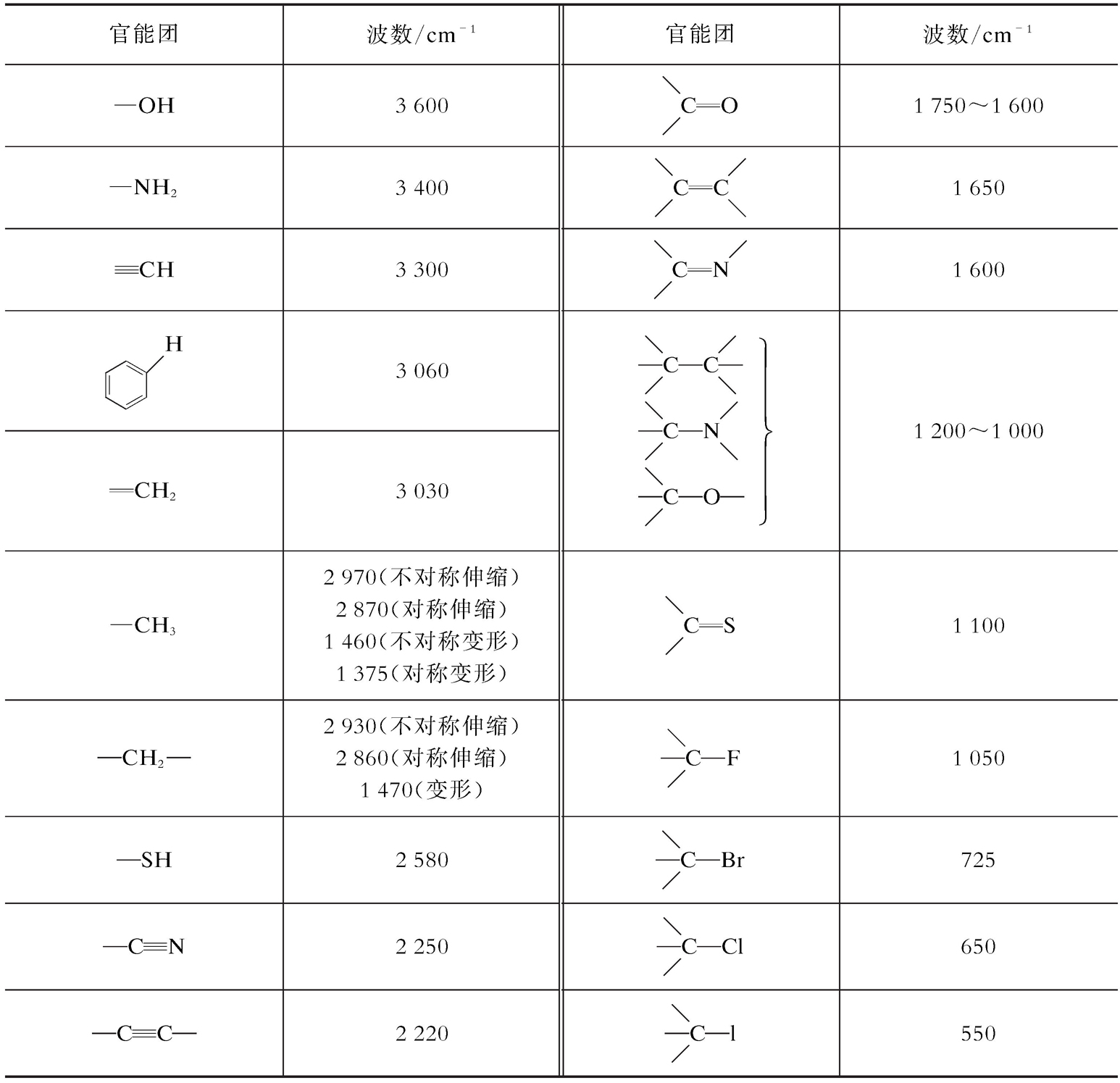
表2-3 部分官能团的特征伸缩频率
拉曼光谱是一种散射光谱。1928年,印度物理学家拉曼(C.V.Raman)首次观察到了拉曼散射效应,即当光穿过透明介质被分子散射的光发生了频率的改变,这一现象称为拉曼散射。拉曼光谱分析法可以获得分子振动、转动方面的信息,因此,适用于物质鉴定以及分子结构分析。在一定条件或状态下,不同的分子拥有独一无二的分子结构,使得拉曼光谱成为物质鉴定的“指纹”。此外,拉曼信号强度正比于样品的浓度,所以也可以作定量分析。相应的分析仪器主要是拉曼光谱仪和拉曼显微镜。
拉曼散射的发生也可以用辐射的量子理论来解释 [3] 。一束具有能量( hν )的光子与分子发生碰撞,如果碰撞是弹性的,光子与分子之间不发生能量交换,光子只改变运动方向而不改变频率 ν ,这种散射叫弹性散射(亦称瑞利散射,Rayleigh scattering)。只有一小部分光子在与分子相互作用时能够交换能量,从而改变了光子的频率,称为非弹性散射(拉曼散射)。分子只有根据量子定律才能获得或失去一定的能量,例如,它的能量变化Δ E ,即分子的振动或/和旋转能量的变化。如果分子获得能量Δ E ,散射光子的能量为 hν -Δ E ,散射光子频率为 ν -Δ E/h ;相反地,如果分子失去能量Δ E ,散射光子的频率为 ν +Δ E/h 。测得的比入射频率低的散射线称为斯托克斯线(Stokes line),高于入射频率的散射线称为反斯托克斯线(anti-Stokes line)(图2-5)。斯托克斯线与反斯托克斯线统称为拉曼谱线,且前者强度通常大于后者。斯托克斯线、反斯托克斯线与入射辐射间的频率差(Δ E / h )称为拉曼位移(Raman shift)。
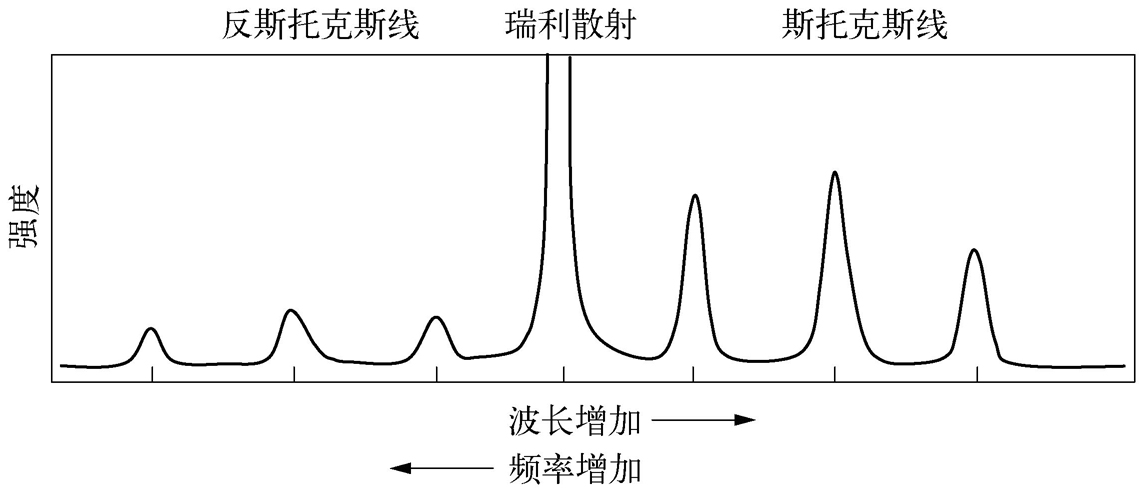
图2-5 拉曼光谱示意图
拉曼效应的经典理论虽然并不完全充分,但值得考虑,因为它引出了对光谱形式基本概念的理解——分子的极化率。当一个分子被置于静电场中时,它会受到某种扭曲,带正电荷的原子核被吸引到电场的负极,电子被吸引到正极。带电中心的分离使分子中产生诱导电偶极矩,从而使分子极化。诱导偶极子的大小可用 μ 表示,即
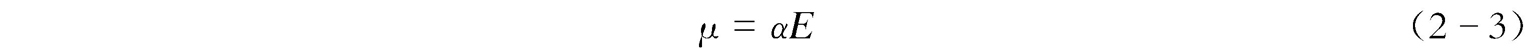
式中, E 为所加电场; α 为极化率(单位电场强度所感应的电偶极矩)。
μ 既取决于电场 E 的大小,也取决于分子被扭曲的容易程度。为了使拉曼激活,分子的跃迁或振动必须引起分子极化率组分的某些变化。若振动未引起分子极化率的改变,无诱导偶极矩,则没有产生拉曼散射,只有瑞利散射。
拉曼谱带的退偏度( ρ )是拉曼光谱的重要参数。激光具有线偏振性,将偏振器放在垂直于激光电矢量的方向上,并分别测定垂直于和平行于入射光方向的散射光谱线强度(分别用 I ⊥ 和 I ∥ 表示),那么两种方向上的谱线强度比称为退偏度。 ρ 的表达式为
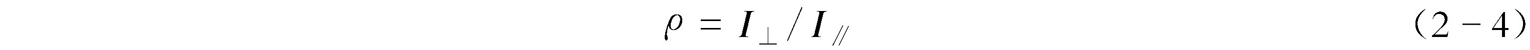
设定入射光为平面偏振光时的退偏度为 ρ p ,入射光为自然光时的退偏度为 ρ n ,对于非全对称振动, ρ p =6/7, ρ n =3/4;若0≤ ρ p <3/4,0≤ ρ n <6/7,该谱带是偏振的,即分子的振动含有非对称振动成分较多。
拉曼光谱被广泛应用于化学、生物以及材料等研究领域。利用拉曼光谱法的偏振特性,可以对顺反异构体进行鉴定。在高聚物的研究中,拉曼光谱还可以提供关于碳链或环的结构信息。在确定异构体(单体异构、位置异构、几何异构和空间异构等)的研究中,拉曼光谱也可以发挥其独特作用。同时,拉曼光谱还是研究生物大分子的有力手段。由于水的拉曼光谱很弱,谱图简单,故拉曼光谱可以在接近自然状态、活性状态下来研究生物大分子的结构及其变化。另外,拉曼光谱广泛应用于表面薄膜(如金刚石、SiO 2 等)的分析与鉴定。
荧光和磷光是两种重要的光致发光形式。光致发光是指物质吸收光子(或电磁波)后,从激发态自发辐射出光子(或电磁波)的过程。荧光与磷光的区分主要根据荧光寿命。磷光的寿命通常比荧光长,但也有例外,有些长寿命的荧光体(如二价铕盐)和短寿命的磷光体(如硫化锌),其持续时间相当(数百纳秒)。与白炽光相比,光致发光不需要很高的温度,而且通常不会产生明显的热量,是冷发光的一种。
前已述及,荧光现象发现得很早,但其合理的解释却较晚,并经历了较长时间。在1819年,克拉克(E.D. Clarke)发现了达勒姆萤石晶体(氟化钙)具有特殊的双色性,反射光的颜色为深蓝色,而透射光的颜色却是强烈的翠绿色,这些观察促进了对荧光概念的发展。1822年,法国矿物学家沃克兰(R.J. Haüy)也观察到了萤石晶体的双色性,并认为这是一种光的散射现象。1833年,布儒斯特(D. Brewster)描述了叶绿素美丽的红色荧光,当用一束光穿过叶子的绿色酒精提取物(主要是叶绿素溶液)时,从侧面可以观察到红色,他认为这与萤石中观测到的现象类似,是一种光的散射。1845年,赫歇尔(J. Herschel)制备了硫酸奎宁溶液,看起来完全透明和无色的溶液,在某些特定的光线照射下,却会呈现出一种极其鲜艳美丽的天蓝色,他提出不同的解释,认为这是一种光的色散现象。直到1852年,斯托克斯(G.G. Stokes)在观察奎宁和叶绿素的荧光发射时发现,它们的发射波长要比入射光的波长更长(此后演变成了“斯托克斯位移”),第一次阐明这种现象是物质吸收了光后重新发出不同波长的光,并于次年首次定义其为荧光(fluorescence) [1] 。然而,需要指出的是,在斯托克斯发表荧光论文的十年前,法国物理学家贝克勒尔(E. Becquerel)在研究硫化钙时就已提出了发射光的波长比入射光的波长长。斯托克斯实验和贝克勒尔实验的区别在于奎宁是荧光,而硫化钙是磷光,但这两种物质都与光致发光有关。由此可见,理论的发展也是逐渐增长和逐步完善的过程。
荧光与磷光的产生过程包括分子的激发和去活化两个阶段。在物质吸收了一定频率的辐射能之后,分子中的电子由原来的基态跃迁至激发态的不同振动能级,这一过程称为激发。大多数分子在室温下处于基态的最低振动能级。通常分子里的价电子数目是偶数,若一半的自旋方向正好和另一半的自旋相反,价电子自旋量子数的总和为零,即 S =0,自旋的多重态 M =2 S +1=1,这类分子我们称它处于单重态,用 S 表示。有些物质的分子正向自旋和反向自旋电子数不等,两者相差为2, S =1, M =3,我们称这类分子处于三重态,用T表示。基态分子和激发态分子都有单重态和三重态两类。单重态的电子基态(S 0 )的分子被激发时,容易跃迁到单重态的电子激发态(S 1 ,S 2 ,…),而不易跃迁到三重态的电子激发态(T 1 ,T 2 ,…),后一种为电子自旋不允许的禁止跃迁。同样,T 0 →T 1 或T 1 →T 0 容易,T 1 →S 0 或S 1 →T 0 难。荧光与磷光所涉及的分子,其基态都处于单重态,具有最低的电子能 [11,12] 。
处于激发态的分子不稳定,它可能通过辐射跃迁和非辐射跃迁的衰变过程而返回基态,也可能经由分子间的作用过程而失活。辐射跃迁的衰变过程伴随着光子的发射,即产生荧光或磷光。非辐射跃迁的衰变过程包括振动弛豫、内转换和系间跨越,这些衰变过程导致激发能转换为热能传递给介质。振动弛豫是指分子将多余的振动能量传递给介质而衰变到同一电子态的最低振动能级的过程;内转换指相同多重态的两个电子态间的非辐射跃迁过程(如
 ,
,
 );系间跨越则指不同多重态的两个电子态间的非辐射跃迁过程(如
);系间跨越则指不同多重态的两个电子态间的非辐射跃迁过程(如
 ,
,
 )。图2-6为分子内发生的激发过程、辐射跃迁和非辐射跃迁衰变过程的示意图。
)。图2-6为分子内发生的激发过程、辐射跃迁和非辐射跃迁衰变过程的示意图。
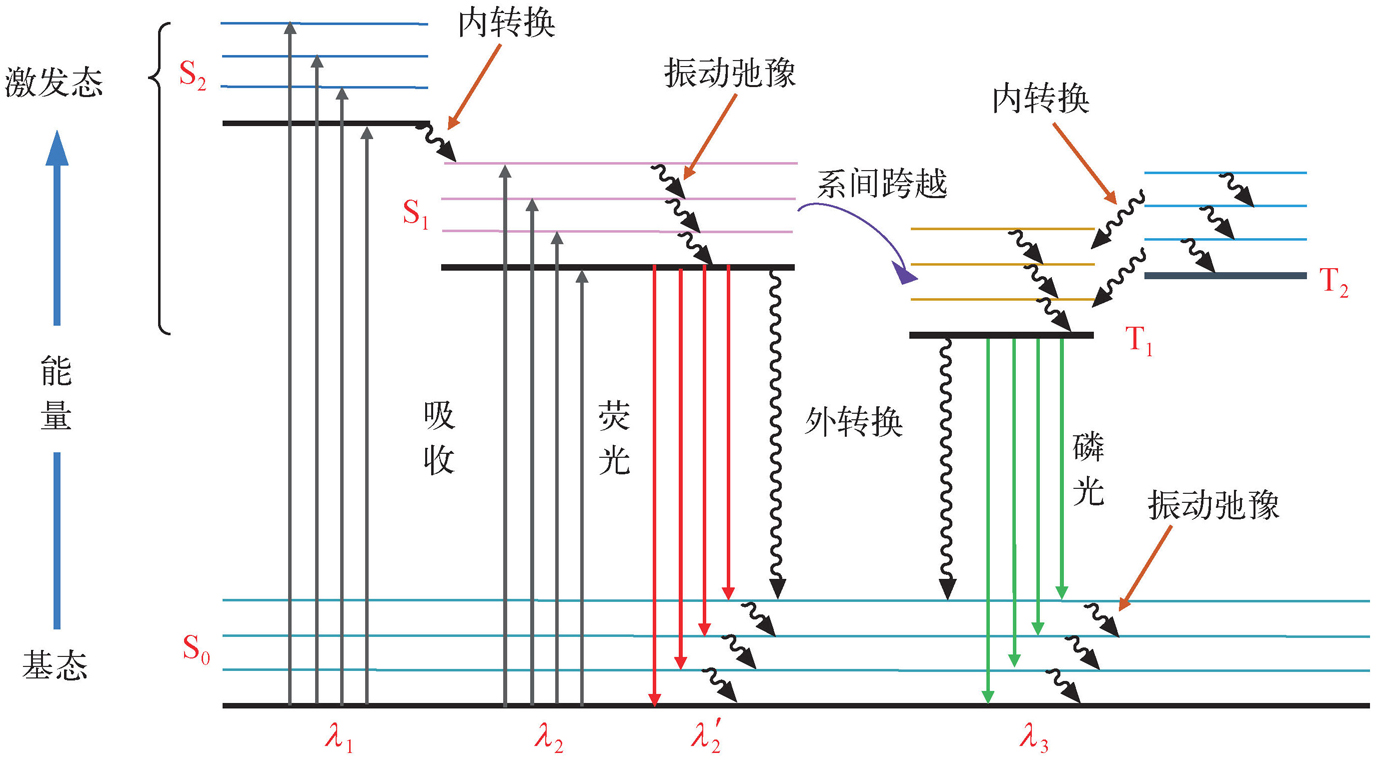
图2-6 分子内发生的激发过程、辐射跃迁和非辐射跃迁衰变过程的示意图
假如分子被激发到S
2
以上的某个电子激发单重态的不同振动能级上,处于这种激发态的分子很快(约10
-14
~10
-12
s)发生振动弛豫而衰变到该电子态的最低振动能级,然后又经由内转换及振动弛豫而衰变到S
1
态的最低振动能级。接着,有如下几种衰变到基态的途径:(1)S
1
→S
0
的辐射跃迁而发射荧光;(2)
 外转换;(3)
外转换;(3)
 系间跨越。而处于T
1
态的最低振动能级的分子,则可能发生
系间跨越。而处于T
1
态的最低振动能级的分子,则可能发生
 的辐射跃迁,从而发射磷光,也可发生
的辐射跃迁,从而发射磷光,也可发生
 的系间跨越或外转换。
的系间跨越或外转换。
按分子激发态的类型分类时,由第一电子激发单重态所产生的辐射跃迁而伴随的发光现象称为荧光;由最低的电子激发三重态发生的辐射跃迁所伴随的发光现象则称为磷光。既然荧光是一种光致发光现象,那么,由于分子对光的选择性吸收,不同波长的入射光便具有不同的激发能或频率。如果固定荧光的发射波长(即测定波长)而不断改变激发光(即入射光)的波长,并记录相应的荧光强度,所得到的荧光强度对激发波长的谱图称为荧光的激发光谱(简称激发光谱)。如果使激发光的波长和强度保持不变,而不断改变荧光的测定波长(即发射波长)并记录相应的荧光强度,所得到的荧光强度对发射波长的谱图则称为荧光的发射光谱(简称发射光谱)。
荧光的激发光谱和发射光谱具有如下特征:①发射光谱的形状通常与激发波长无关,但其强度与激发波长有关;②激发光谱和发射光谱的轮廓呈镜像关系;③发射峰位总是大于激发峰位,这种峰位之间的波长差称为斯托克斯位移(Stokes shift)。斯托克斯位移的存在说明激发态分子在返回到基态之前经历了振动弛豫、内转换等过程而消耗了部分激发能。图2-7为苝的苯溶液和奎宁的稀硫酸溶液的激发光谱和发射光谱,可以看出,它们的激发光谱和发射光谱之间大致存在着镜像对称的关系。
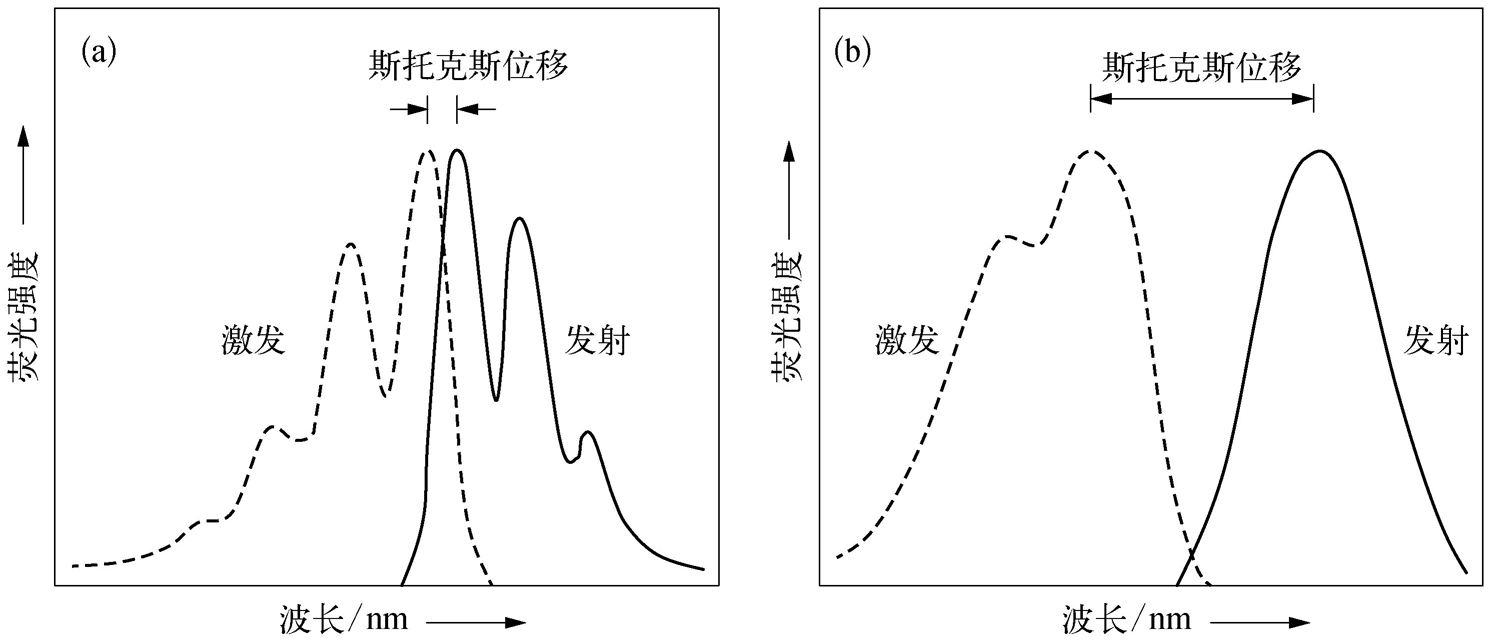
图2-7 苝的苯溶液(a)和奎宁的稀硫酸溶液(b)的激发光谱和发射光谱 [11]
荧光既然是物质在吸收光子之后所发射的辐射,因而溶液的荧光强度( I f )与该溶液吸收的光强度( I n )及物质的荧光量子产率( Φ )有关,即
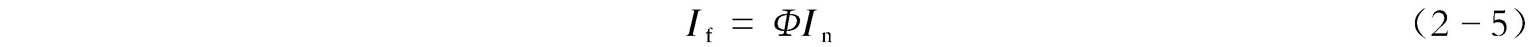
荧光量子产率 Φ 的定义是:荧光物质所发射的荧光的光子数与其所吸收的激发光的光子数之比值。而吸收的光强度等于入射光的光强度( I 0 )减去透射的光强度( I t ),即
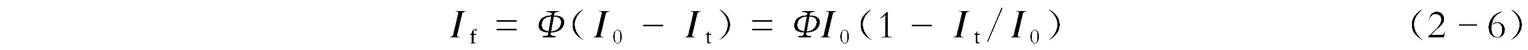
由朗伯-比尔定律可知: A =-lg( I t / I 0 )= εbc ,即 I t / I 0 =10 - εbc =e - abc ( a 为待定数),于是 I f = ΦI 0 (1--e - abc )。而e - abc 可表示为
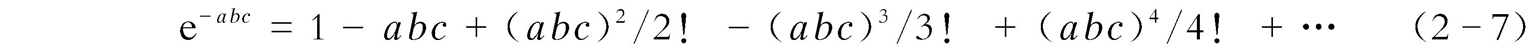
当 abc 非常小(≪0.05)时,e - abc ≈1- abc ,代入上述相关方程式之后,可得:
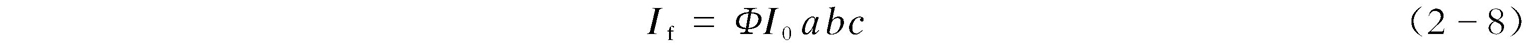
又由10 - εbc =e - abc 得:lg(10 - εbc )=lg(e - abc ),即 a = ε /lge= ε /lg2.718=2.303 ε ;当与摩尔吸光系数 ε 关联时,则有:
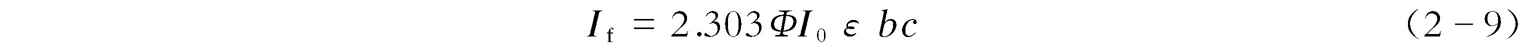
式(2-9)即荧光定量分析的依据和公式。可以看出,在一定的波长及强度的激发光照射下,当某种荧光物质的浓度足够低使得其对激发光的吸光度很小时,所测溶液的荧光强度才与该荧光物质的浓度成正比。如果 εbc ≥0.05时,则荧光强度和溶液的浓度不一定呈线性关系,此时应考虑幂级数中的二次方甚至三次方项。
荧光光谱分析具有很高的灵敏度,通常比吸收光谱分析高两个数量级,适用于痕量物质的测定(纳摩尔浓度水平),相对误差为5%~10%。与吸收光谱法不同,荧光分析中激发光源、检测器通常彼此垂直,不在同一直线上。荧光分析在测试中需要考虑多种因素的影响,如荧光探针本身的特性、仪器与环境等因素 [2] 。
荧光光谱法由于其具备高灵敏度、高时空分辨率等优势,且在许多情况下克服了放射性示踪剂所造成的环境污染与费用高的问题,近年来已成为化学、环境、材料、生物、医学、物理学等众多学科领域,特别是生命科学领域中最重要的研究与分析工具之一,并广泛应用于医学诊断、流式细胞术、法医鉴定和遗传分析、安全标志、防伪检测(防伪文件、钞票、艺术品)等方面。而且,荧光光谱分析在细胞和分子成像方面的应用更是取得了显著的发展,如荧光成像可以揭示细胞内分子的分布与变化,甚至可以达到单分子检测水平。