下载掌阅APP，畅读海量书库
立即打开
随着时间的变化，交通流呈现出不同的波动特性，反映在交叉口上即出现不同交通状态交替的现象。随着汽车保有量的不断攀升，城市交叉口交通状态变化日趋明显。因此，城市交叉口不同状态下的交通控制理论与方法的研究有其特殊性。
研究不同交通状态下交叉口交通流特性和信号控制，首先应从交叉口交通状态的界定入手，对此国外的相关研究开展较早。本章参考文献［1］认为过饱和状态是当一个交叉口所有进口道的到达流量大于交叉口的通行能力，即在绿灯放行时间排队的车辆无法全部释放，排队不断增加。本章参考文献［2］将无排队溢出作为交叉口是否处于过饱和状态的关键判别指标。
国内对于交通状态判别的研究则相对起步较晚。林瑜等 ［3］ 采用行车速度与排队长度的空间占有比例作为拥挤程度的判别指标，并应用模糊算法对拥挤程度进行量化，从而设计了隶属度函数和判断规则的形式，形成了过饱和交通的状态量化方法。王殿海等 ［4］ 提出了路网宏观交通状态参数的选取原则，并通过二流理论给出宏观交通流参数之间的数学关系，从而建立了路网宏观交通流状态判别模型。
综上所述，现有研究多是从车辆排队溢出、交通供需或交叉口饱和度等角度对交叉口交通状态进行界定的，并未深入考虑信号控制本身对交叉口交通状态的影响。本节则选择从交叉口相位的流量和所获绿信比之间的关系入手，采用综合投影的方法对交叉口的交通状态进行界定，同时该方法还能给出绿信比的取值范围，能为交通控制提供更便利的条件。
1.流量-绿信比三维关系
选取典型两相位控制的单交叉口进行建模研究，交叉口的相位分别为“东西直行”和“南北直行”，如图2-1所示。
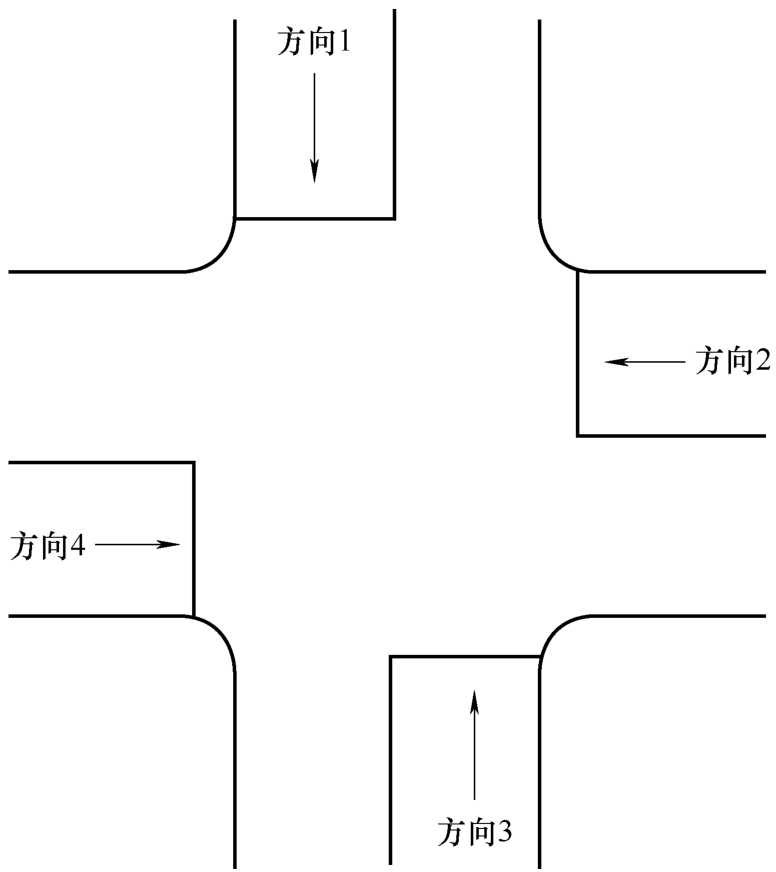
图2-1 交叉口相位图
其中各方向的排队长度定义如下：
相位1 北直行和南直行的排队长度分别为 x 1，3 （ k ）和 x 3，1 （ k ）。
相位2 东直行和西直行的排队长度分别为 x 2，4 （ k ）和 x 4，2 （ k ）。
为了便于简化系统分析和控制策略的设计，选择相向而行的两个行驶方向中排队长度较长的作为相位排队长度变量 x i （ k ），具体定义为
x i （ k ）=max{ x i ， i +2 （ k ）， x i +2， i （ k ）}， i =1，2
交叉口各相位之间由于切换序列的存在是离散的，但各相位的排队长度在采样周期内是连续变化的。因此可建立以下模型：
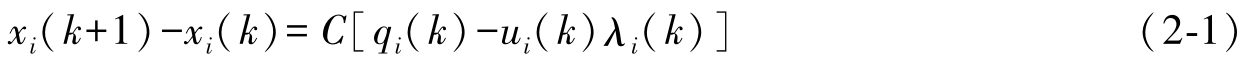
式中， x i （ k ）为相位 i 的排队长度； C 为信号周期； q i （ k ）为相位 i 的流入率； u i （ k ）为相位 i 的流出率； λ i （ k ）为相位 i 的绿信比。
由式（2-1）所示的相位到达流量、离开流量和绿信比之间的关系，可以建立流量-绿信比关系图，如图2-2所示。图2-2中，
λ
1
为相位1的绿信比；
N
1
为相位1的流量；
N
2
为相位2的流量；为表达完整性，
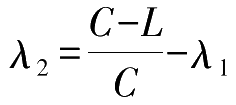，为相位2的绿信比；
L
表示总的损失时间。
如图2-2所示，在Δ OYW 中，边 OW 所在平面由 N 1 和 λ 1 组成，表示相位1流量 N 1 所对应的最小绿信比 λ 1 的集合。即，当相位1流量为 N 1 时，为保证相位1车辆能完全清空的最小绿信比为 λ 1 。边 YW 在平面 N 1 —N 2 上的投影为 YX 。 YX 表示相位1和相位2最大流量的连线，即交叉口各相位所能获得流量的集合。因此， YW 由 N 1 、 N 2 和 λ 1 组成，表示各相位在临界流量上所获得绿信比集合。因此，Δ OYW 围成的区域表示相位1不同流量所获最小绿信比的集合。在Δ YZW 中，边 YZ 所在平面由 N 2 和 λ 1 组成，表示相位2流量所对应的最小绿信比 λ 2 ，也代表了相位1所对应的最大绿信比 λ 1 。因此，Δ YZW 围成的区域表示相位1不同流量所获最大绿信比的集合。则有，相位1的流量的变化，其绿信比取值范围为［Δ OYW ，Δ YZW ］。
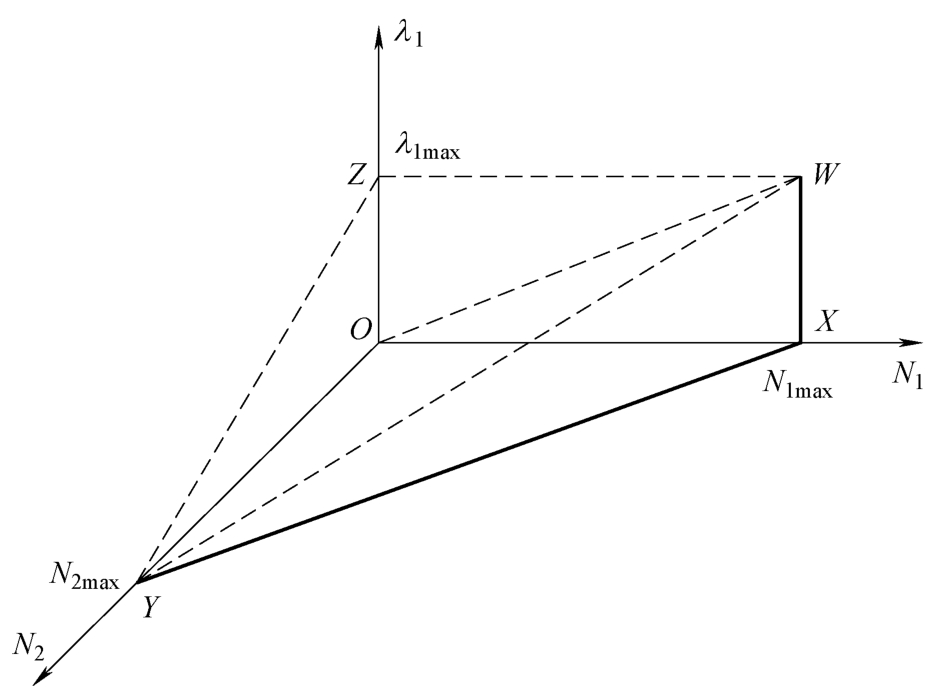
图2-2 流量-绿信比关系图
Δ OWX 为锥体 OWXY 在 N 1 —λ 1 平面上的投影。其表示，当相位1流量固定，随着绿信比 λ 1 增加，相位1的通行能力增加。边 OW 为对应流量随绿信比最小值所形成的边。那么，有
Δ OYZ 为锥体 OWYZ 在 N 2 —λ 1 平面上的投影。当相位2流量固定，随着绿信比 λ 1 增加，相位2的通行能力减小。边 YZ 为对应流量随绿信比最小值所形成的边。那么，有
Δ
OYX
为锥体
OWYZ
在
N
1
—N
2
平面上的投影。其表示相位1和相位2之间在
λ
1
+
λ
2
=
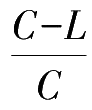条件下的约束关系。那么，有
2.两相位控制交叉口交通状态分析
采用三维关系图和排队时间图对交叉口欠饱和、临界饱和与过饱和三种状态进行详细分析。如图2-3所示，当交叉口流量点{ N 1 ， N 2 ， λ 1 }处于锥体 OYXW 在 N 1 N 2 平面的投影内部时，即点 A 位置，随着相位1的流量 N 1 减小，其获得的绿信比 λ 1 也在减小；相位2所容纳的流量也会增加，其获得的绿信比1 -λ 1 也会增大，并且在相位绿灯时间内周期积累的车辆能完全消散。同理，可以点 B 为例对临界饱和状态进行说明，以点 C 为例对过饱和状态进行说明。
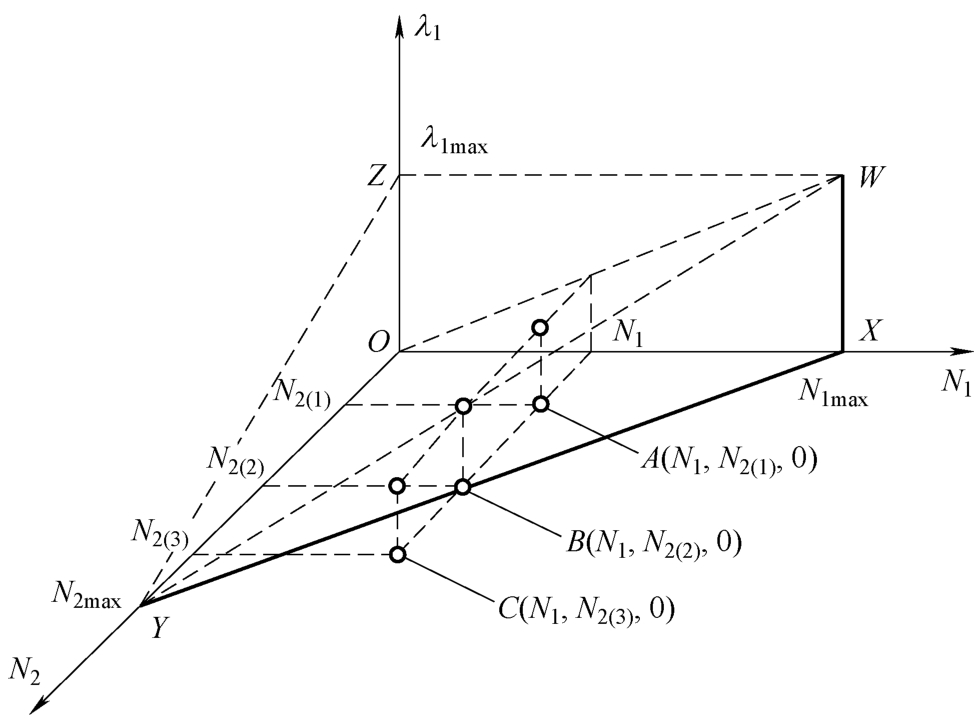
图2-3 固定相位1的三维关系图
如图2-3所示，固定相位1的流量为 N 1 ，改变相位2的流量为 N 2（1） 、 N 2（2） 和 N 2（3） ，分别得到坐标点 A { N 1 ， N 2（1） ，0}、 B { N 1 ， N 2（2） ，0}和 C { N 1 ， N 2（3） ，0}。
（1）对点 A 的分析
如图2-4所示，当相位1和相位2的流量为{ N 1 ， N 2（1） }时，相位1存在绿信比 λ 1 ∈［ λ 1min（1） ， λ 1max（1） ］使得各相位所有到达车辆均能在相位绿灯时间内通过交叉口。
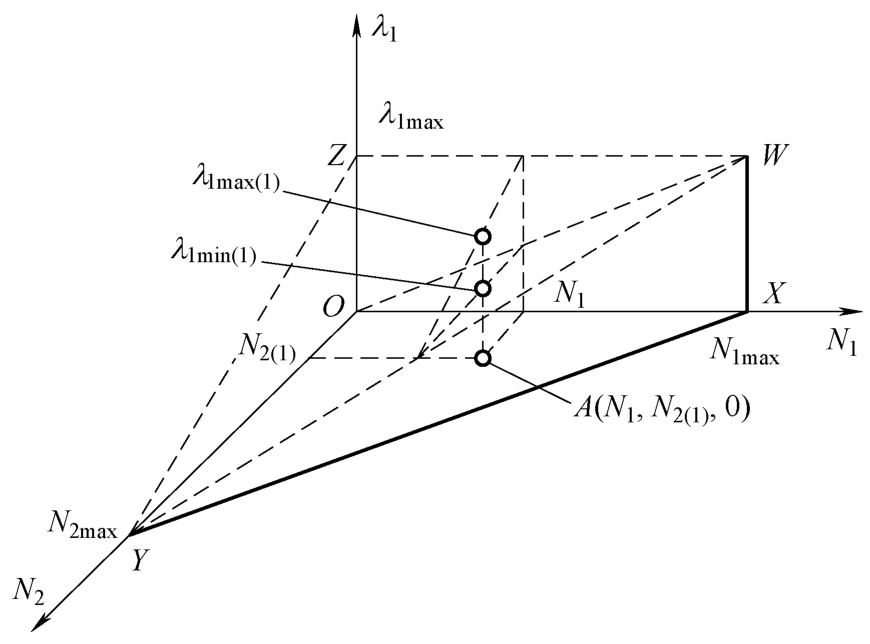
图2-4 欠饱和三维关系图
图2-5所示的排队-时间图为相位1的欠饱和排队-时间图。可以看出，若交叉口无初始排队，当相位1和相位2的流量为{ N 1 ， N 2（1） }时，在各自的绿灯时间能完全清空到达的车辆，并且相位1的绿灯时间值为 g 1 =［ g 1min（1） ， g 1max（1） ］。
（2）对点 B 的分析
如图2-6所示，当相位1和相位2的流量为{ N 1 ， N 2（2） }时，相位1存在绿信比 λ 1 = λ 1min（2） = λ 1max（2） 使得各相位所有到达车辆均能在相位绿灯时间内通过交叉口。
如图2-7所示，若交叉口无初始排队，当相位1和相位2的流量为{ N 1 ， N 2（2） }时，在各自的绿灯时间刚好完全清空到达的车辆，并且相位1的绿灯时间值为 g 1 = g 1min（2） = g 1max（2） 。
（3）对点 C 的分析
如图2-8所示，当相位1和相位2的流量为{ N 1 ， N 2（3） }时，相位1不存在绿信比 λ 1 ≥ λ 1min（3） 使得各相位所有到达车辆均能在相位绿灯时间内通过交叉口。
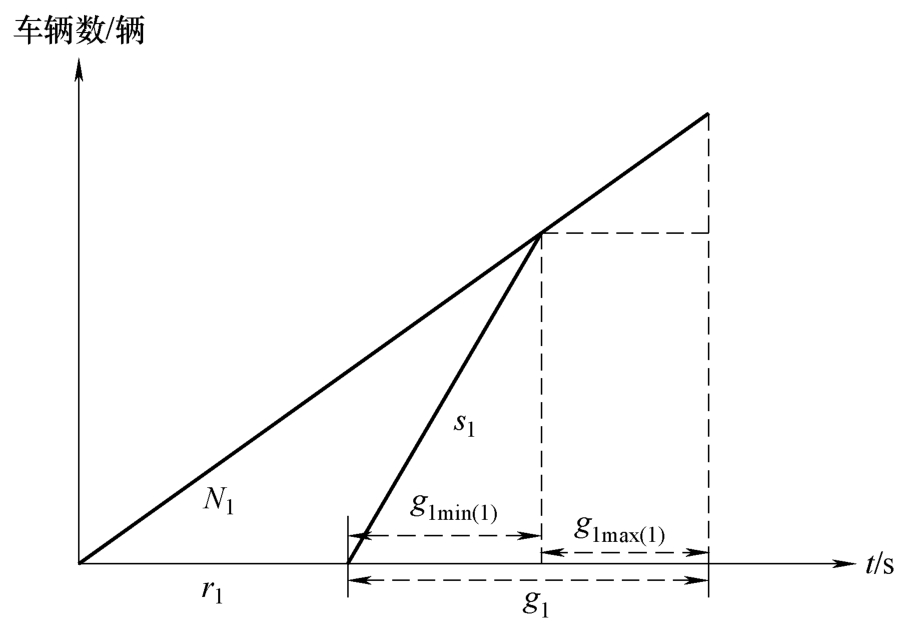
图2-5 相位1的欠饱和排队-时间图
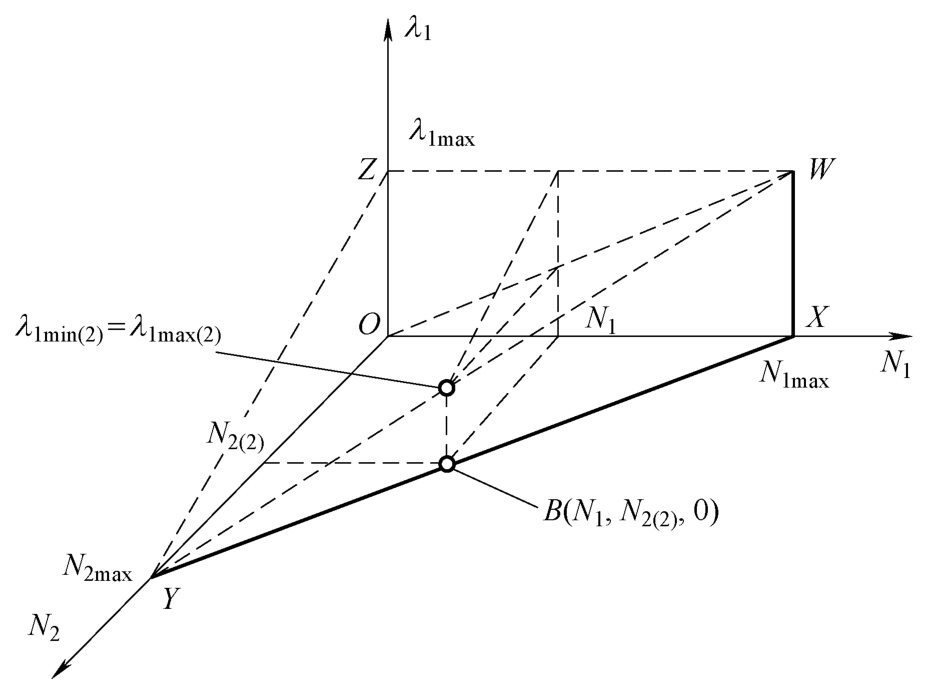
图2-6 临界饱和三维关系图
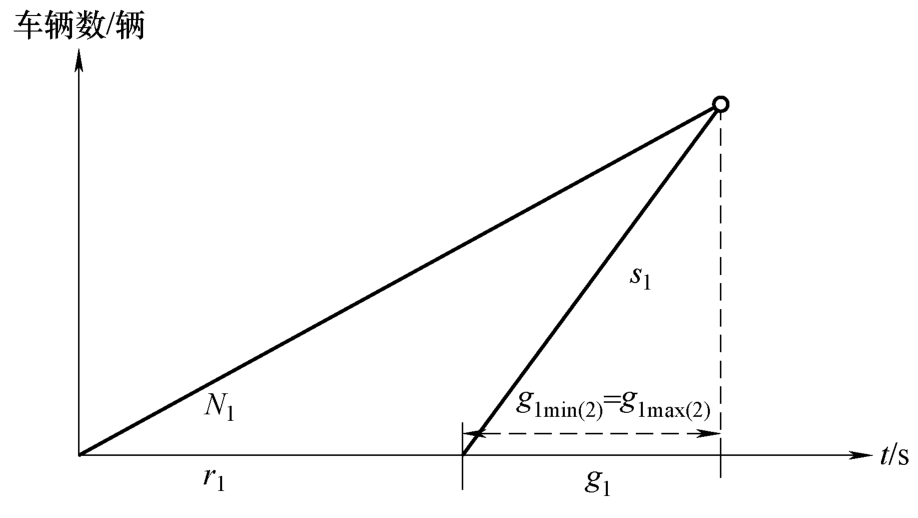
图2-7 临界饱和排队-时间图
如图2-9所示，若交叉口无初始排队，当相位1和相位2的流量为{ N 1 ， N 2（3） }时，相位1在绿灯时间为 g 1 = g 1min（3） = g 1max（3） 可以完全清空到达的车辆，但相位2在绿灯时间为 g 2 =［0， C-L-g 1 ］的范围内取任何值均不能清空到达的车辆。
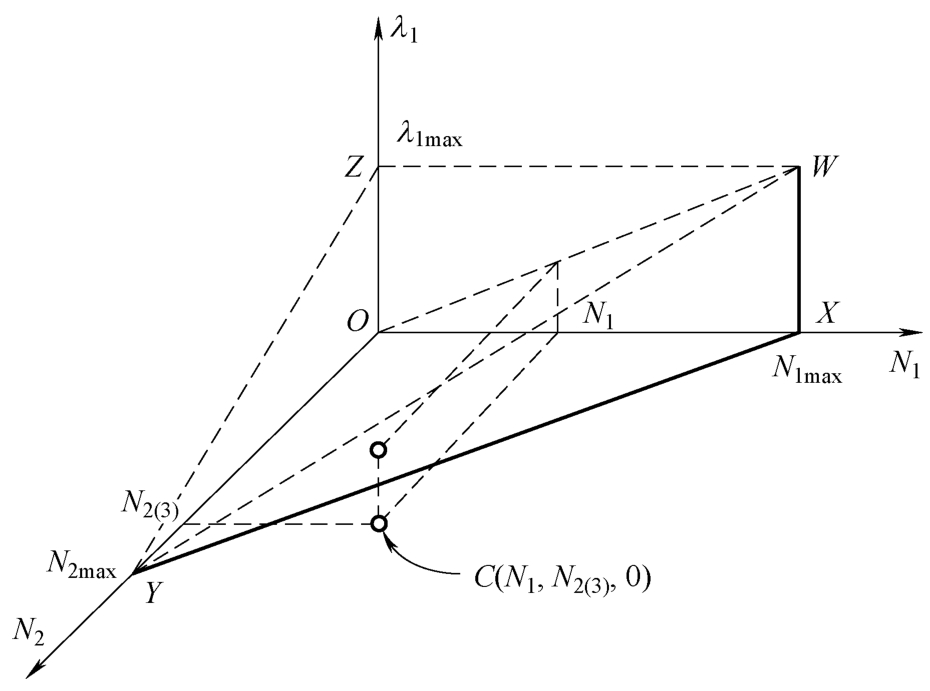
图2-8 过饱和三维关系图
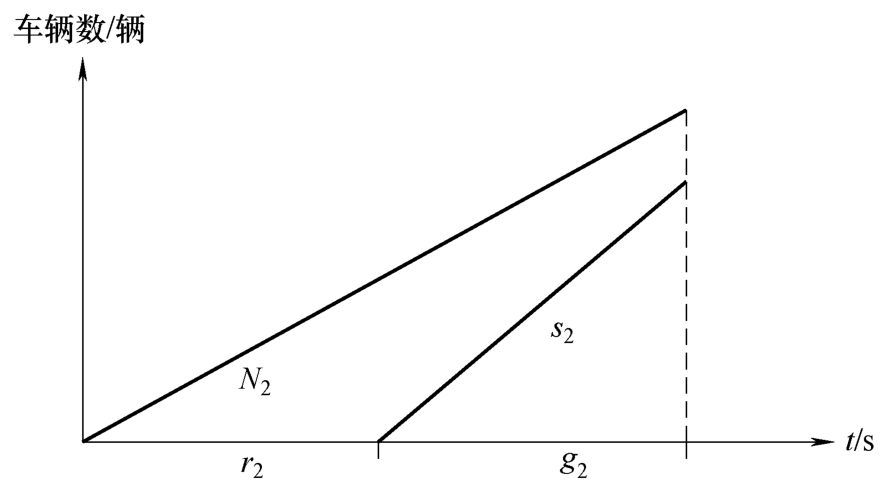
图2-9 过饱和排队-时间图
同理，固定相位2可得到类似结论，此处不予重复。
1.多相位控制交叉口维度确定
由2.2.1节可知，将相位流量 N 1 、 N 2 和相位1的绿信比 λ 1 组成为一个具有三维关系的流量-绿信比图，如图2-10所示。
令 N 1 = x 、 N 2 = y 、 λ 1 = z ，将“流量-绿信比三维关系图”等同于三维空间坐标图。对于一个三维空间坐标点{ x ， y ， z }必在该坐标图内，可知三维关系坐标点{ N 1 ， N 2 ， λ 1 }也必在流量-绿信比三维关系图内。因此，可以进行以下描述：一个典型的2相位控制交叉口可用“流量-绿信比三维关系图”进行分析，内部点坐标为{ N 1 ， N 2 ， λ 1 }。
对于一个3相位控制交叉口，其相位流量为
N
1
、
N
2
、
N
3
，相位绿信比为
λ
1
、
λ
2
、
λ
3
。令
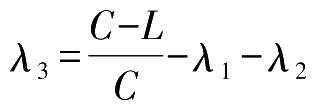，则3相位控制交叉口构成的“流量-绿信比关系图”应该由
N
1
、
N
2
、
N
3
、
λ
1
和
λ
2
组成，则应是一个五维关系图，其内部坐标点为{
N
1
，
N
2
，
N
3
，
λ
1
，
λ
2
}。同理，对于一个4相位控制交叉口的“流量-绿信比关系图”应该由
N
1
、
N
2
、
N
3
、
N
4
、
λ
1
、
λ
2
和
λ
3
组成，是一个七维关系图，内部坐标点为{
N
1
，
N
2
，
N
3
，
N
4
，
λ
1
，
λ
2
，
λ
3
}。由此可以知道，交叉口相位数量与维度的关系由{
N
i
，
λ
i
-1
}决定，因此
n
相位控制交叉口“流量-绿信比关系图”为一个2
n
-1维关系图。
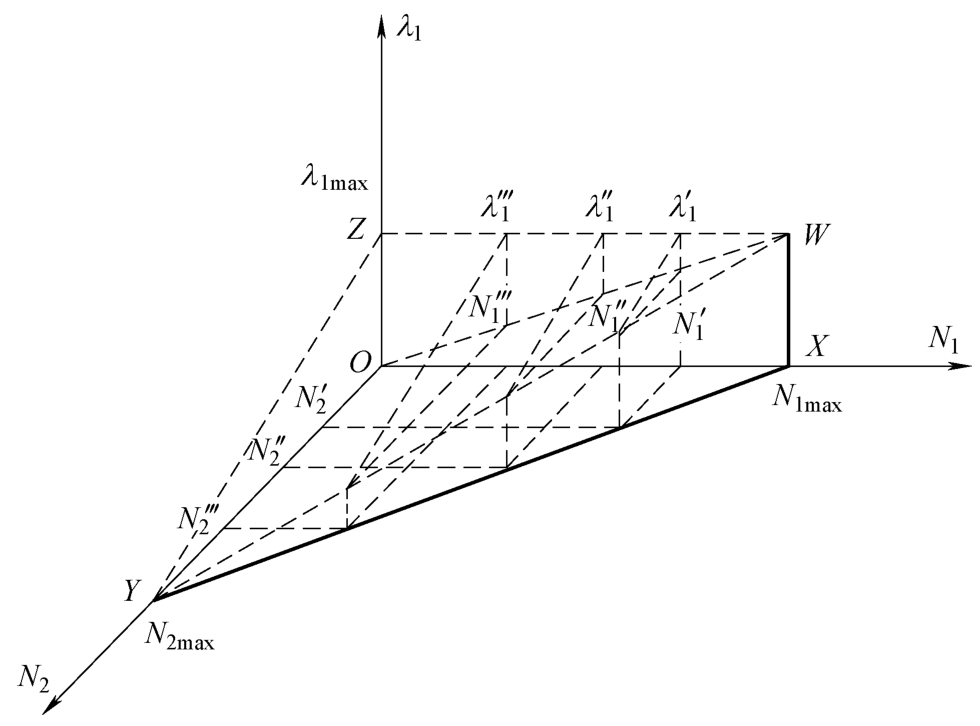
图2-10 流量-绿信比三维关系全景图
2.多维关系分解及投影
详细分析了典型两相位交叉口下相位和绿信比之间的关系，就可得出不同流量下相位绿信比的设置范围，如图2-10所示，并基于此对交叉口交通状态进行重新界定。
然而，对于超过三维关系的多相位控制交叉口，无法采用2.2.2节的方法对交叉口进行分析。但通过研究发现，多维关系可以被适当分解为若干个三维关系，并表示为“三维关系集合”。将所得的三维关系集合在一个标准三维关系坐标内进行投影，投影所得的多面体的面便是交叉口饱和度的临界面。
3.多维关系分解
多维关系分解是分析多相位交叉口交通状态的关键，利用相位之间的排列组合，可形成多种三维关系。
假设交叉口相位顺序一定，周期循环从相位1到相位1。对于2相位交叉口，其流量和绿信比组成为{ N 1 ， N 2 ， λ 1 }，则可以形成一个三维关系空间，所以可分解的三维关系空间数为1；对于3相位控制交叉口，其流量和绿信比组成为{ N 1 ， N 2 ， N 3 ， λ 1 ， λ 2 }，则可以形成一个五维关系空间，所以可分解的三维关系空间数为3，分别为{ N 1 ， N 2 ， λ 1 }、{ N 1 ， N 3 ， λ 1 }、{ N 2 ， N 3 ， λ 2 }；对于4相位控制交叉口，其流量和绿信比组成为{ N 1 ， N 2 ， N 3 ， N 4 ， λ 1 ， λ 2 ， λ 3 }，则可以形成一个七维关系空间，所以可分解的三维关系空间数为4，分别为{ N 1 ， N 2 ， λ 1 }、{ N 2 ， N 3 ， λ 2 }、{ N 3 ， N 4 ， λ 3 }、{ N 4 ， N 1 ， λ 1 }，由此可知一个4相位七维关系空间能分解的三维关系空间的个数等于其相位的个数。因此，可得到 n 相位形成的2 n -1维关系空间能分解成三维关系空间的个数为 n 。
4.分解后投影及反投影
多维关系空间分解原则：分解出来的每个三维关系空间称为一个子交叉口；被分解的交叉口称为父交叉口；对每个子交叉口进行分析，则假设不包含的相位为空相位。
如图2-11所示，以三相位五维关系空间为例。子交叉口为①、②、③，即分解出来的3个三维关系空间。图中，子交叉口①描述的是相位1流量
N
1
、相位2流量
N
2
和相位1绿信比
λ
1
之间的关系。假设该交叉口是典型的2相位交叉口，即相位3为空相位，有
λ
1
+
λ
2
=
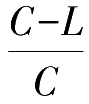。同理，子交叉口②中，相位1为空相位，有
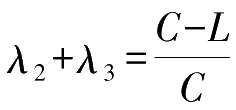；子交叉口③中，相位2为空相位，有
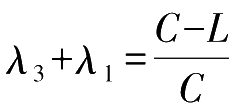。这样可避免统一分析三者之间的关系带来的复杂性。
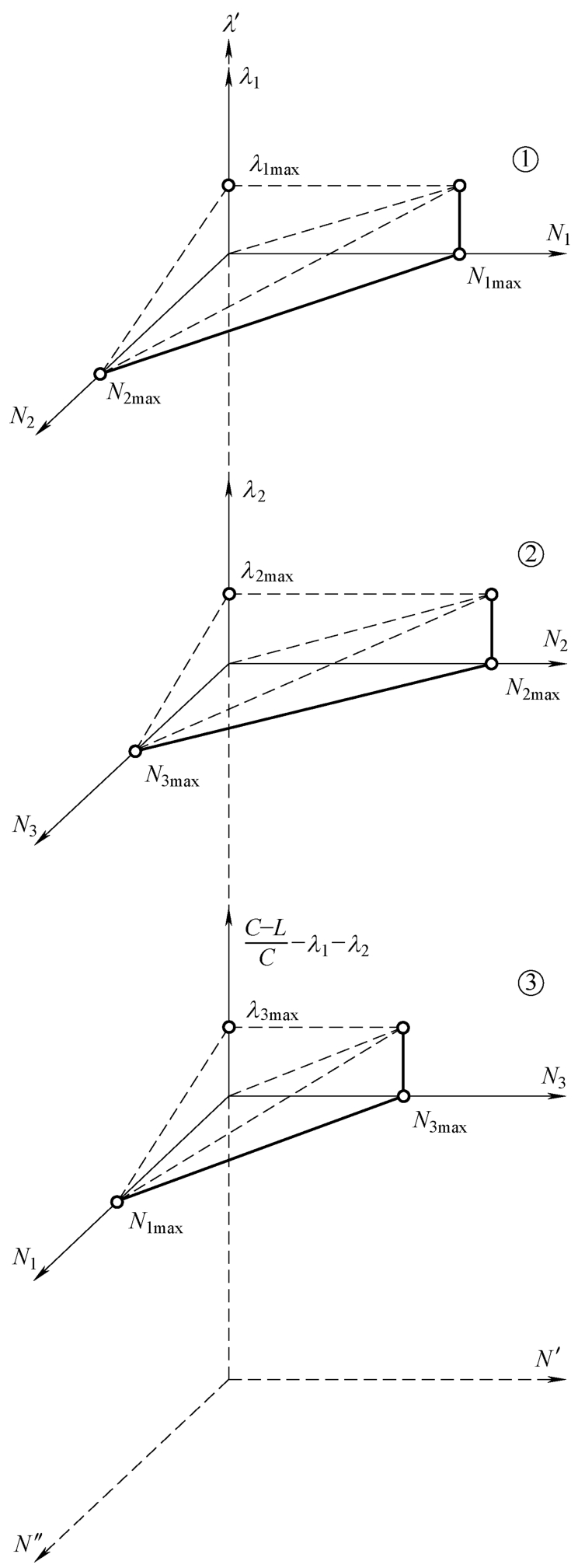
图2-11 三相五维关系空间图
（1）分解后投影
将多相位交叉口分解所得到的三维关系空间按照 N i = N ′、 N j = N ″、 λ n = λ ′对应投影到一个标准三维坐标空间内，可以形成一个投影空间的集合，该集合便是多相位交叉口欠饱和交通状态的集合。两相位控制交叉口所能分解的三维关系空间只有一个，就是其所形成的流量-绿信比三维关系图，因此无须投影。下面以三相五维关系空间为例进行详细描述。
如图2-12所示，通过上述分析三相五维关系空间可以分解为3个三维关系空间，得到三维关系空间集合{①，②，③}，将该集合在标准三维坐标空间上进行投影，可得到用于分析交叉口饱和状态的多面体。
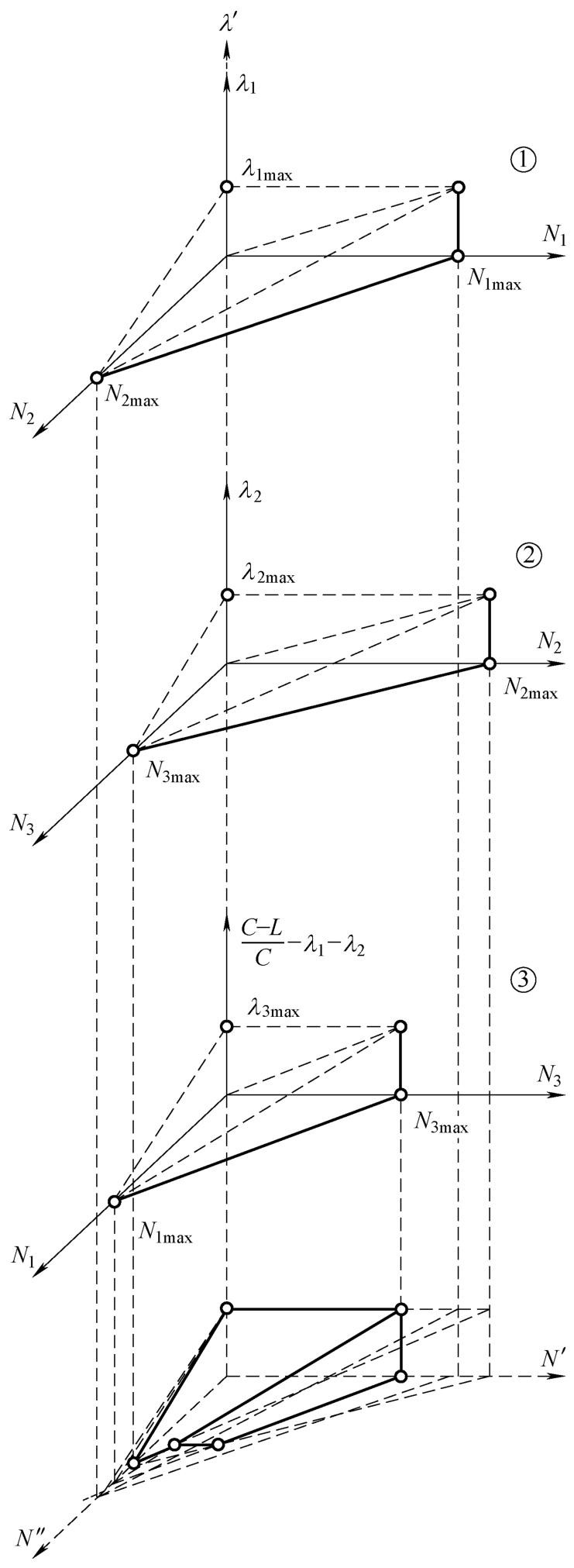
图2-12 三相五维关系空间投影
将图2-12所示的投影多面体 ABFEOCD 进行局部放大，如图2-13所示。
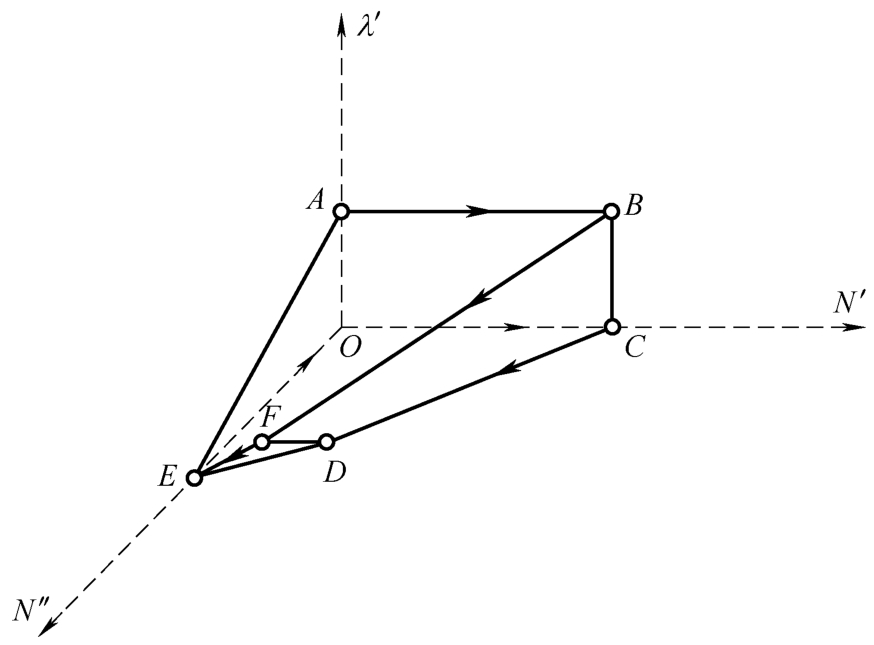
图2-13 投影局部放大
（2）反投影
如图2-14所示，在投影形成的多面体内部 ABFEDCO 取一个点的集合{ N ′， N ″， λ ′}，反投影到三维关系空间集合体{①，②，③}中，如图2-15所示。
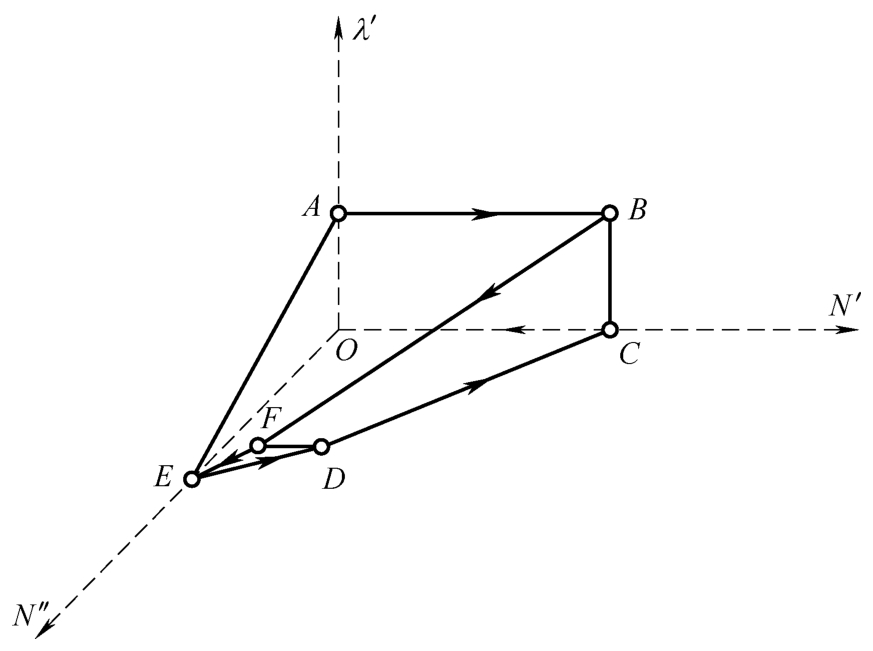
图2-14 反投影
通过反投影，在每个三维关系空间内部都能得到一个投影点，进而能得到每个点的三维关系坐标 a :{ N 1 ， N 2 ， λ 1 }、 b :{ N 2 ， N 3 ， λ 2 }、 c :{ N 3 ， N 1 ， λ 1 }，从而便得到了五维关系空间内的点的坐标{ N 1 ， N 2 ， N 3 ， λ 1 ， λ 2 }。
在进行饱和状态判断时，要将交叉口流量{ N 1 ， N 2 ， N 3 ， λ 1 ， λ 2 }，分成三维关系坐标点{ N 1 ， N 2 ， λ 1 }、{ N 2 ， N 3 ， λ 2 }、{ N 3 ， N 1 ， λ 1 }，组成坐标点集合{{ N 1 ， N 2 ， λ 1 }，{ N 2 ， N 3 ， λ 2 }，{ N 3 ， N 1 ， λ 1 }}进行判断，才能得出交叉口的饱和状态。其中每个坐标点首先必须满足2相位的三维关系空间的要求。
5.多相位控制交叉口交通状态判别
综合上述分析，给出如下多相位控制交叉口的交通状态判别方法：
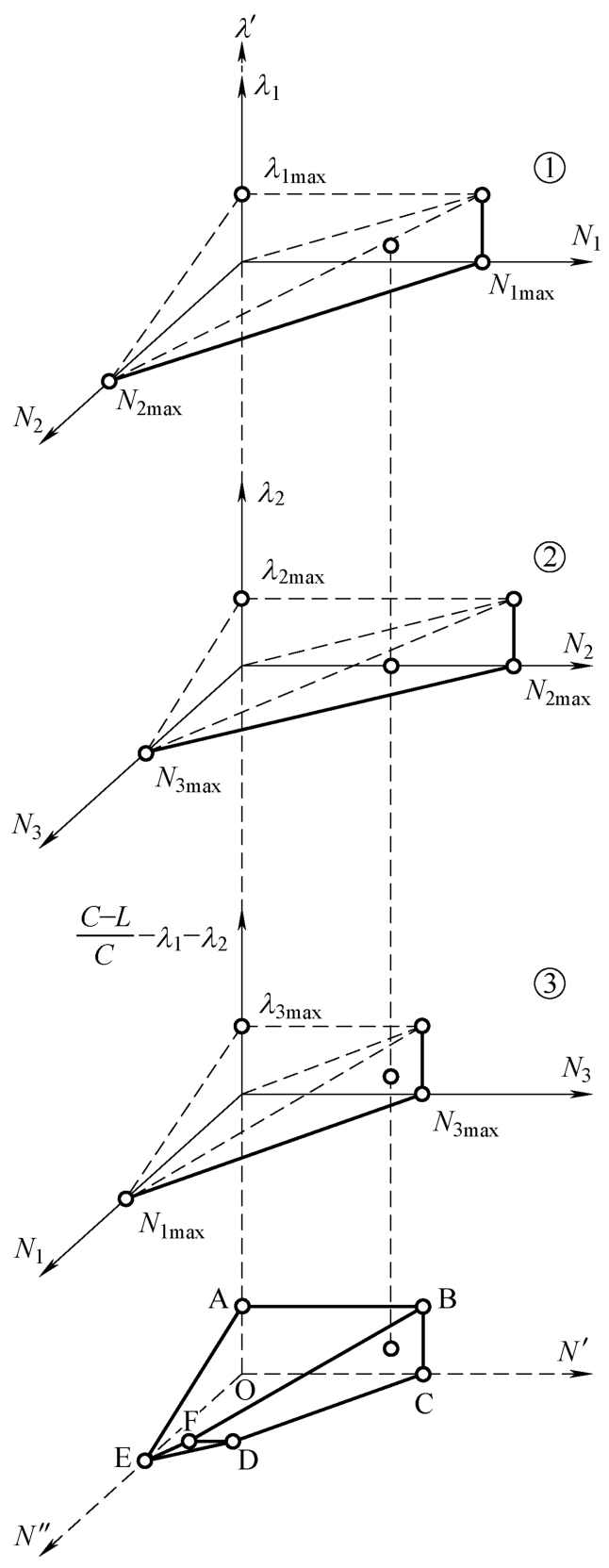
图2-15 三相五维关系空间反投影
1）如果存在一组绿信比区间使得各相位在周期内积累的车辆能完全消散，这种情况称为欠饱和状态，且该状态下可计算得到该组绿信比区间。
2）如果存在唯一的一组绿信比使得各相位在周期内积累的车辆恰好完全消散，这种情况称为临界饱和状态，且该状态下可计算得到该组的绿信比。
3）如果不存在任何一个绿信比使得各相位在周期内积累的车辆能完全消散，这种情况称为过饱和状态，且该状态下不可计算得到任何组的绿信比。
为了验证本节所提出的交叉口交通状态判别方法的准确性，选取北京市学院南路和交大东路交叉口东西和南北两相位的交通数据进行仿真验证。该交叉口两个方向5:00～21:00的交通流数据如图2-16所示［（每15min采集一次，折合成标准车当量数（pcu）］。
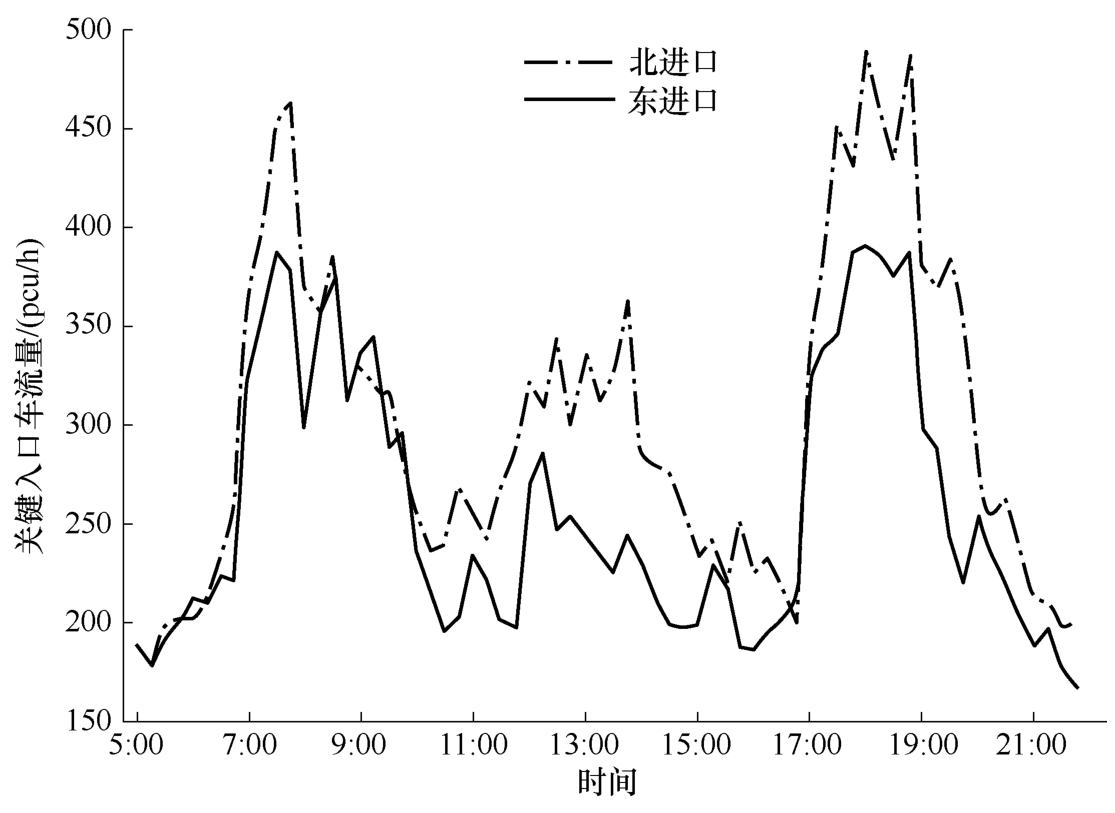
图2-16 学院南路和交大东路交叉口两个方向5:00~21:00的交通流数据
利用所提方法对学院南路和交大东路交叉口的交通状态进行界定，其中该交叉口周期 C =70，南北方向的绿信比 λ 1 =0.44，饱和流量 N 1 =1025pcu/h，东西方向的饱和流量 N 2 =712pcu/h，如图2-17所示。图中，黑色点位表示交叉口处于欠饱和状态下的北进口和东进口流量，其余部分为交叉口处于过饱和状态。
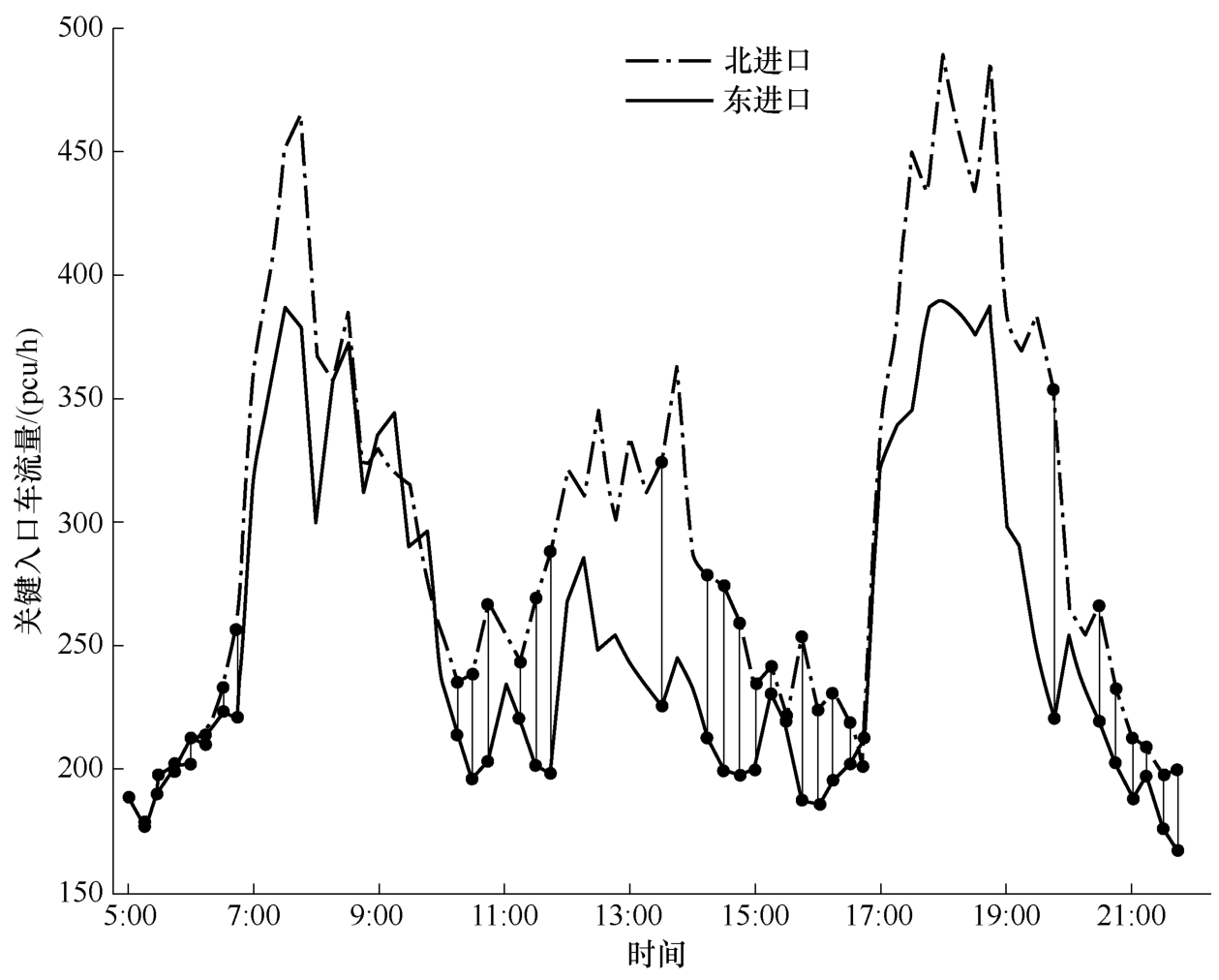
图2-17 学院南路和交大东路交叉口交通状态变化
利用所提方法对学院南路和交大东路交叉口的交通状态进行界定，同时不限定各关键方向的绿信比，可得图2-18～图2-20所示的流量分布。
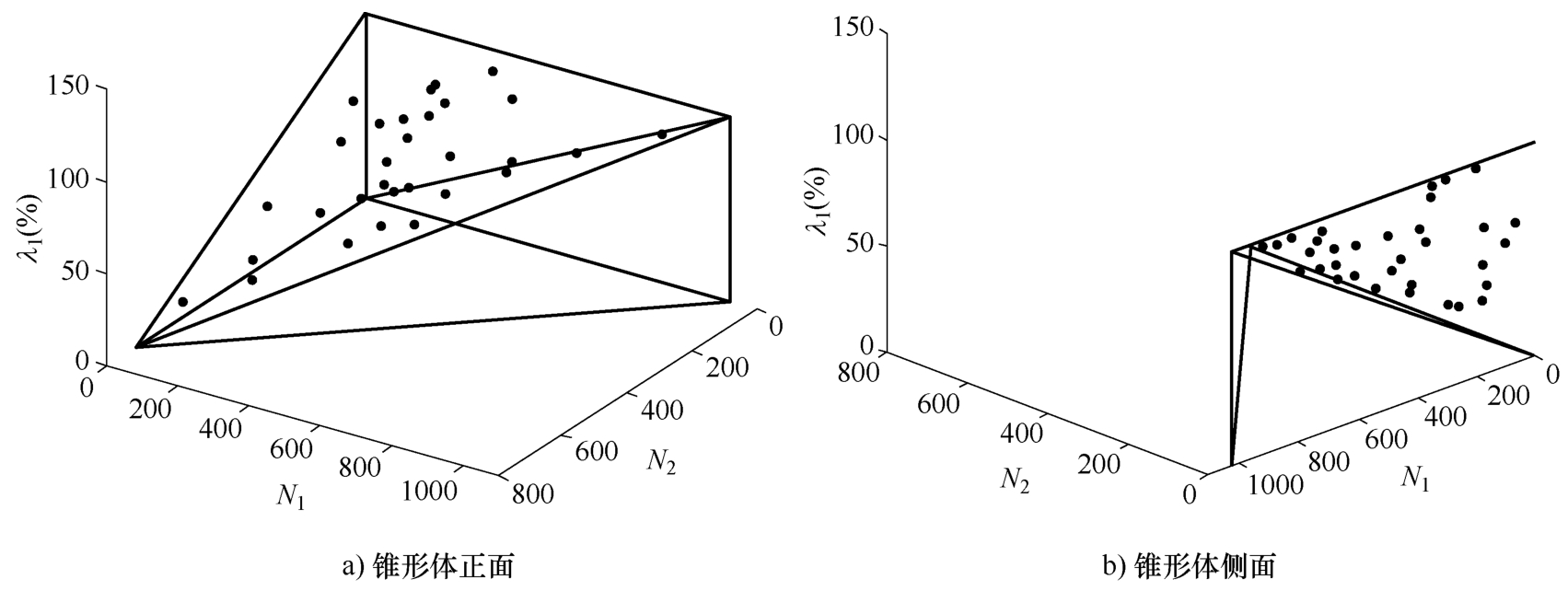
图2-18 交叉口欠饱和状态流量分布
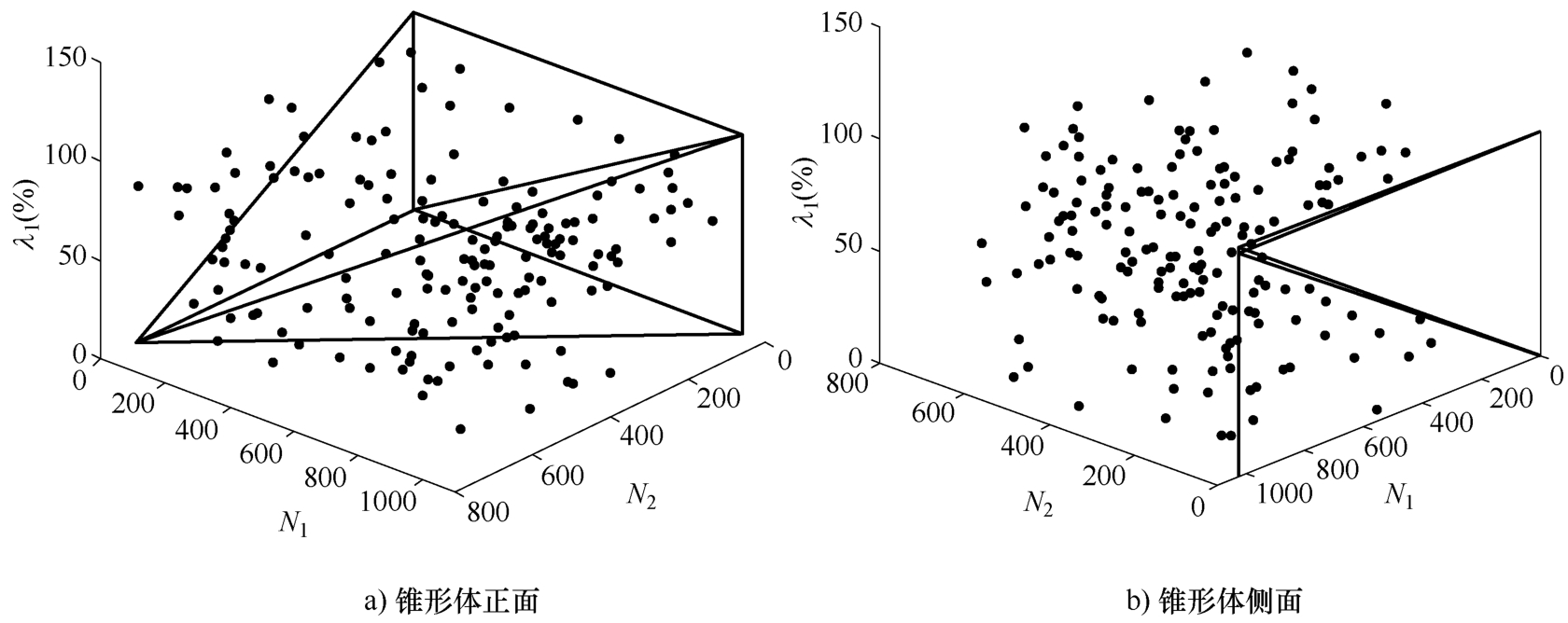
图2-19 交叉口过饱和状态流量分布
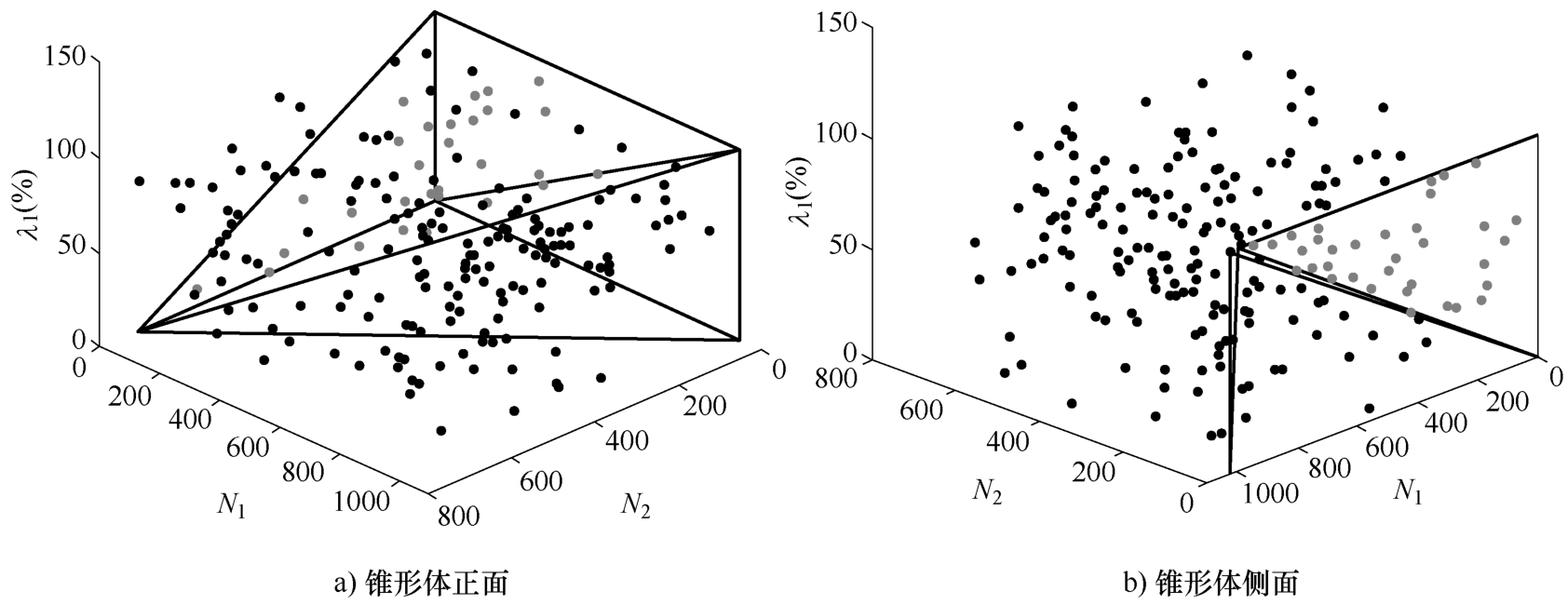
图2-20 交叉口不同交通状态流量分布
如图2-18所示，处于锥形体内部的点表示，在5:00～21:00获得流量中使交叉口处于欠饱和状态的流量-绿信比点位。如图2-19所示，在锥形体外部的点表示，在5:00～21:00获得流量中使交叉口处于过饱和状态的流量-绿信比点位。如图2-20所示，学院南路和交大东路交叉口5:00～21:00所有交通流量下呈现的不同交通状态。采用本节所提出的方法可以快速确定交叉口交通状态，同时又能确定交叉口各相位的绿信比变化范围，可为不同交通状态下的交叉口信号控制提供依据。
本节，从交叉口各相位流量和绿信比之间的关系入手，建立了交叉口排队模型，重点对两相位控制交叉口的交通状态进行了详细分析；然后，采用综合投影的方法，给出了多相位控制交叉口交通状态界定方法。以两相位控制的交叉口为例对本节所提出的方法进行了验证，结果显示该方法具有可行性。