




截至目前,我们一直从静态的角度来讨论线性规划问题,即假设各个系数 a i j 、 b i 和 c j 都是已知的常数。然而,实际上这些系数往往是一些估计值或预测值,因此不可避免带有一定的误差;另外,现实世界的不断变化(如市场条件的改变、工艺技术的改进等)也使这些系数具有不确定性。为了提高线性规划模型及其求解结果的可靠性,有必要研究这些系数发生变化时对最优解(或最优基)的影响,这就是灵敏度分析或优化后分析的有关内容。本书的讨论仅仅是一个入门介绍。
假定目标函数只有一个系数 c j 发生变化,模型中的其他系数保持不变。我们要确定 c j 在什么范围内变化时,原问题的最优解不变,称这个范围为 c j 的可变范围。
例 5 求第 2 章例 1 中目标函数系数 c 2 的可变范围。
解:本例的最优单纯形表如表 3 -2 所示(参见表 2 -4):
表 3 -2
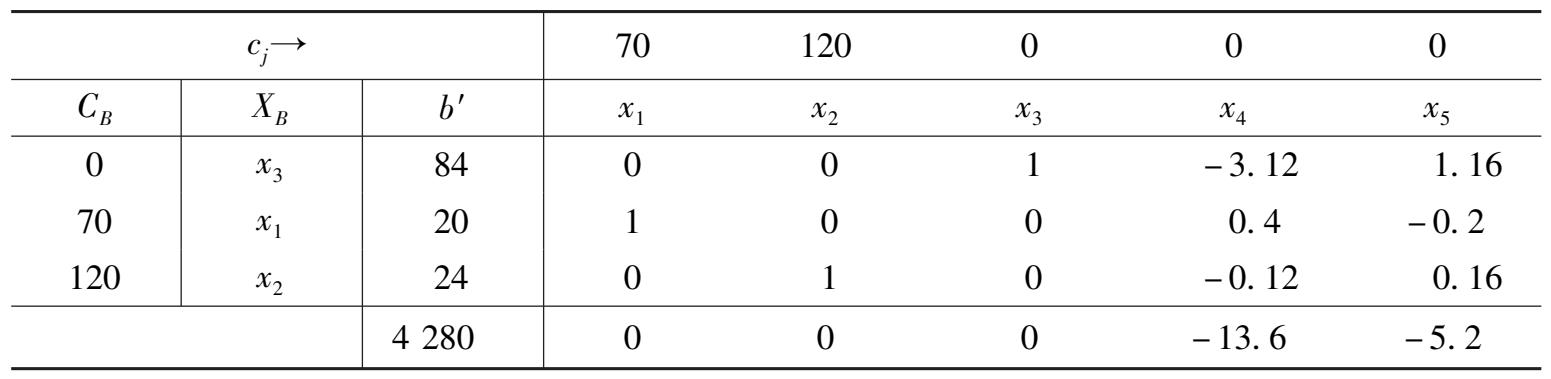
在表 3 -2 中, x 2 的目标函数系数 c 2 的当前值为 120。现把这个系数的值用符号 c 2 代替。此时,相应的单纯形表如表 3 -3 所示(注意表 3 -3 与表 3 -2 的差别只在检验数行)。
表 3 -3

为使问题的最优解不变,只需表 3 -3 中的检验数满足最优性准则,即 c 2 要满足不等式组:
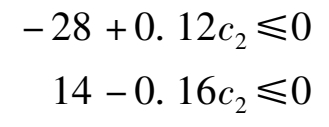
由此可得到 c 2 的可变范围:87.5≤ c 2 ≤233.33。
若 c 2 的值超出可变范围,则最优性条件遭到破坏,这时,需利用单纯形法求出新的最优解。
读者不难求出目标函数其余系数的可变范围。
假定右端项中只有一个参数 b i 发生变化,模型中的其他系数保持不变。由于右端项的变化只会引起基变量值和目标函数值的变化,而不会引起检验数的变化,因此,我们只需讨论右端项变化对最优基变量的影响。具体处理时,我们要确定 b i 在什么范围内变化,最优基变量保持不变,称这个范围为 b i 的可变范围。
注意最优基变量保持不变与最优基不变是同一回事,因此,可以看出
b
i
的可变范围也是影子价格
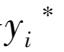 保持不变的范围及有效范围。
保持不变的范围及有效范围。
例 6 求例 5 中右端项 b 3 的可变范围。
从最优表(见表 3 -2)知最优基变量为 x 3 , x 1 , x 2 ,最优基为(注意这里提到的是初始数据,可由表 2 -4 看出):
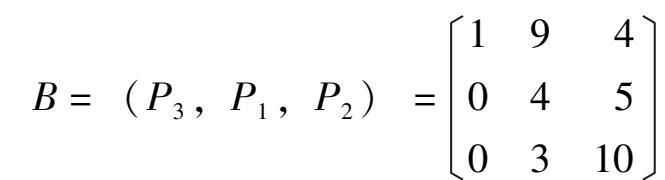
根据单纯形法旋转变换的代数原理,不难看出初始基变量 x 3 , x 4 , x 5 在最优表中相应的列构成最优基 B 的逆矩阵,即

在本例中, b 3 的当前值为 300 (也是用初始数据),现用 b 3 代替这个数值,则最优表(见表 3 -2)中除了 b′ 这列以外,其他数据不变。而 b′ 由

若要保持 B 的最优基地位,应保证基变量的值非负,即要求
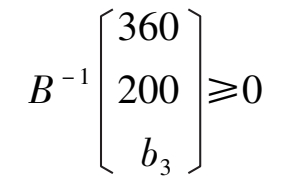
由此可得到不等式组:
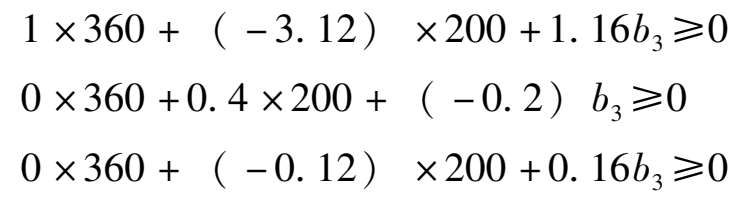
最后解得:227.586≤
b
3
≤400。这是最优基(变量)保持不变的范围,也是上一节所得到影子价格
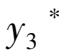 = 5.2 保持不变的范围及有效范围。
= 5.2 保持不变的范围及有效范围。
图3 -1是QM for Windows输出的第 2 章例 1 的目标函数系数与右端项的可变范围(执行“Solve”命令后,在菜单栏的“Window”中选择“Ranging”可得)。 Excel软件的“规划求解结果”对话框中的“报告”方块也有“敏感性报告”选项供用户选择(见图2 -11)。
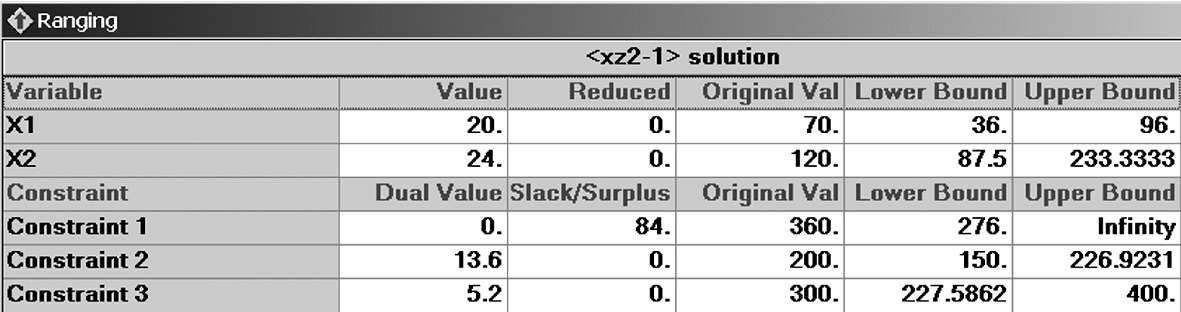
图 3 -1
图 3 -2 是使用Excel解第 2 章例 1 (也是本章例 5 与例 6)时输入的电子表格模型工作表,其中可变单元格(代表决策变量)为B4 和C4,目标单元格为D6。请读者在各单元格D8、 D9 和D10 中输入有关公式,并在“规划求解参数”对话框中输入相应的信息。
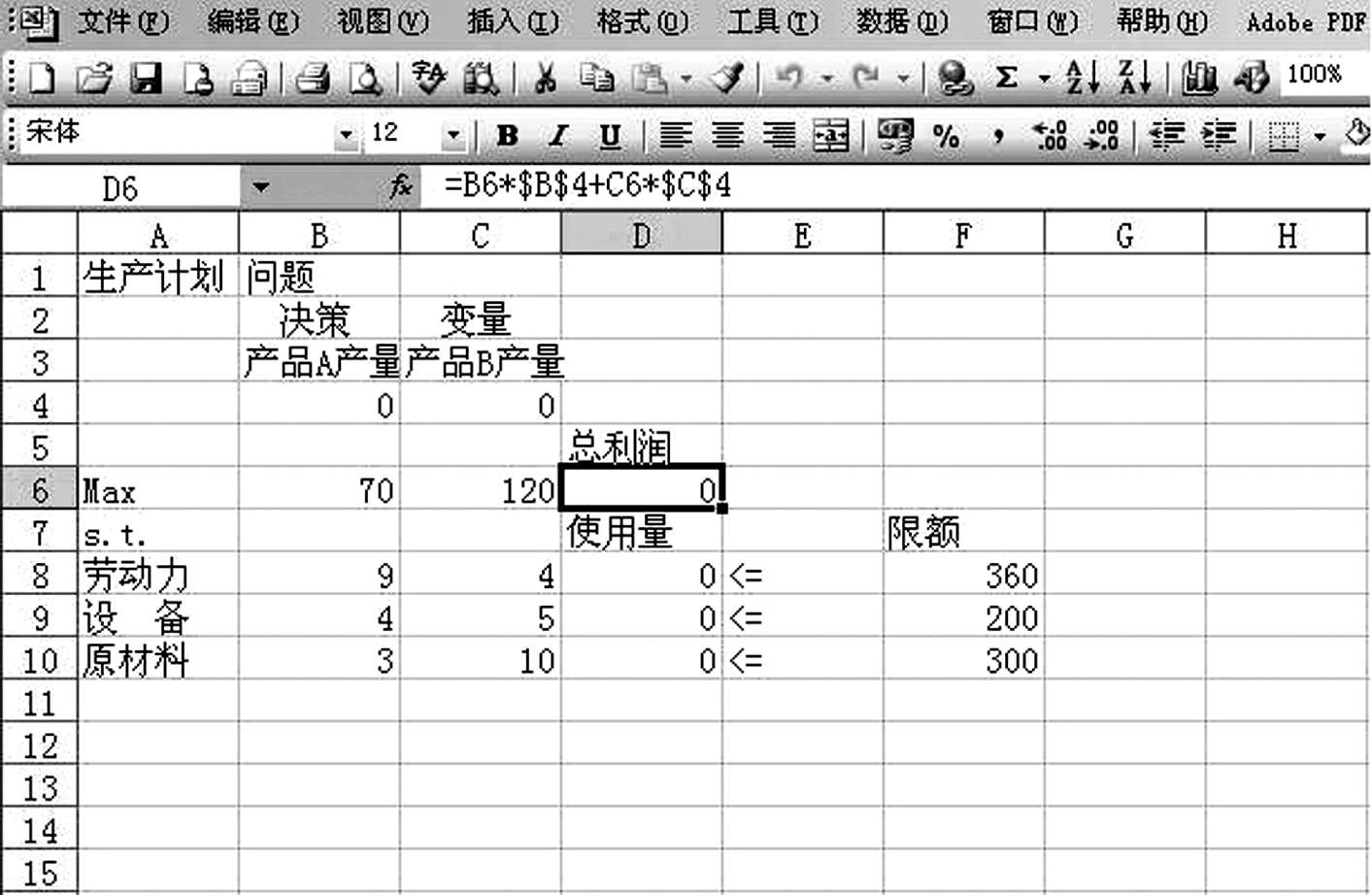
图 3 -2
图 3 -3 是求解后有关灵敏度分析内容的输出。
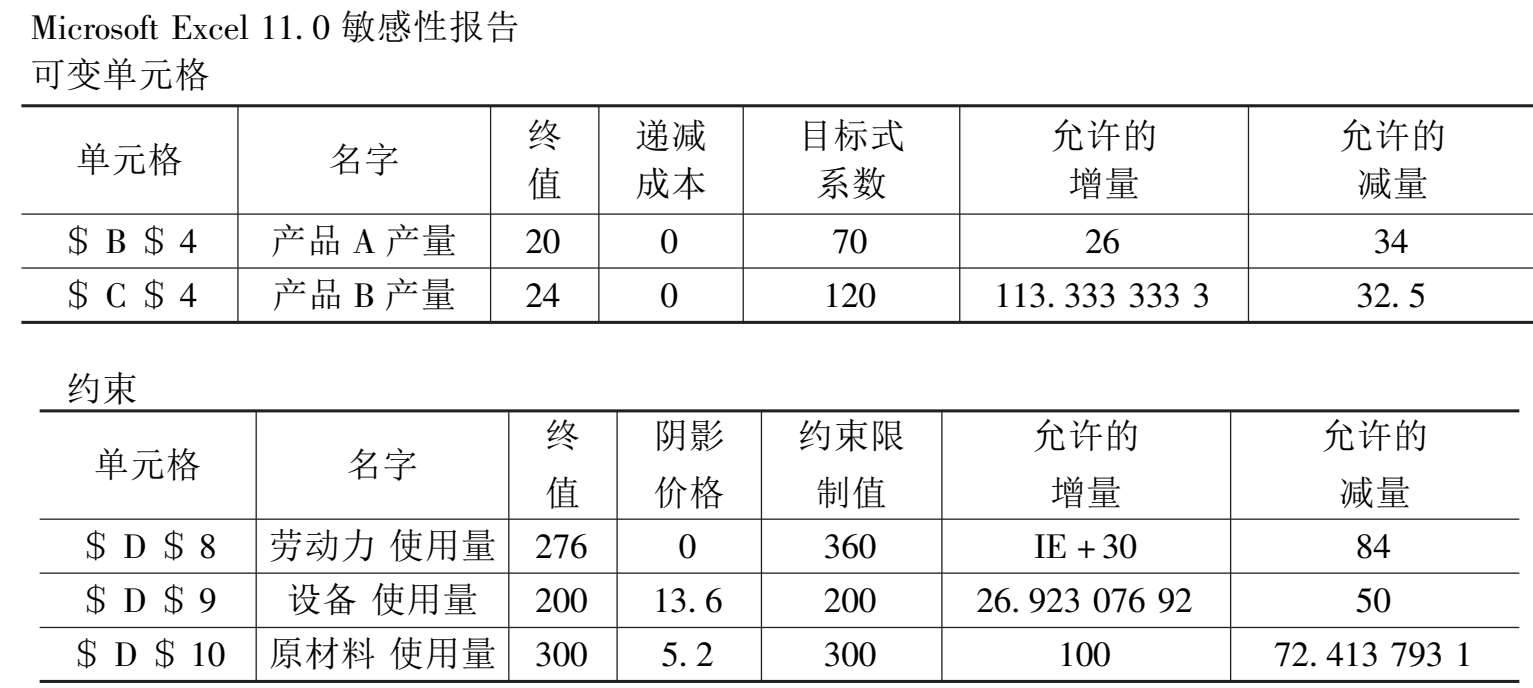
图 3 -3
前面的灵敏度分析都是以单个参数发生变化为前提的,但实际上往往有多个参数同时发生变化。本小节讨论多个目标函数系数 c j 变化的灵敏度分析。
假设某些 c j 变化为 c j + Δ c j ,根据前面的单参数灵敏度分析,我们可确定这些 c j 单个变化的可变范围,假定为:

记指标集
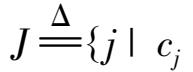 发生变化且
x
j
为基变量}。多参数变化灵敏度分析的具体步骤如下:
发生变化且
x
j
为基变量}。多参数变化灵敏度分析的具体步骤如下:
(1)检查发生变化的 c j 是否都满足条件 LB j ≤ c j + Δ c j ≤ UB j ,若都满足则进入步骤(2);否则,最优解会发生变化,进入步骤(4)。
(2)若 J 只包含一个指标,进入步骤(3);否则对于每个指标 j ∈ J ,计算单个变化比率:
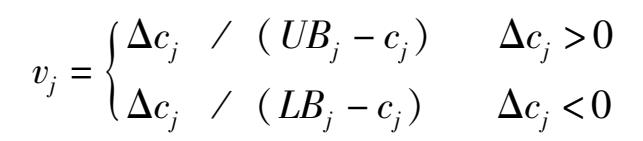
再计算总变化比率
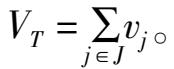 若
V
T
≤1,进入步骤(3);否则进入步骤(4)。
若
V
T
≤1,进入步骤(3);否则进入步骤(4)。
(3)作出最优解保持不变的结论,计算变化后的目标值(目标值的变化量为
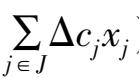 ),停止。
),停止。
(4)从原最优单纯形表出发,修改相应参数的值后进行迭代。
例 7 市场条件发生变化影响最优生产计划。
对第 2 章例 1 的问题,如果由于市场条件发生变化,产品A的单位利润降为 53 元,产品B的单位利润升至 160 元,最优生产计划是否会发生变化?如果产品A的单位利润升为 95 元,而产品B的单位利润降到 90 元,又将如何?
解:产品A单位利润降为 53 元,则Δ c 1 = -17;产品B单位利润升至 160 元,则Δ c 2 = 40。使用图 3 -1 的结果计算单个变化比率和总变化比率:

所以最优生产计划不会改变,总利润的相应增量为(-17)×20 +40 ×24 =620 (元)。
如果产品A和B的单位利润分别变为 95 元和 90 元,则Δ c 1 =25,Δ c 2 = -30,经计算:
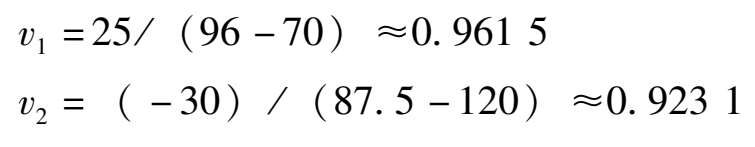
V T = v 1 + v 2 > 1,所以最优解会发生变化。从原最优表(见表 3 -2)出发,修改相应的参数值得新单纯形表,经迭代后(建议读者自行列表计算),可求得变化后的最优解 x 1 = 34.482 7, x 2 = 12.413 8;最优值 z = 4 393.1。
除了上述的灵敏度分析形式外,实际问题还会产生诸如增加新变量、增加新约束条件或系数 a ij 发生变化等灵敏度分析。其处理方法是从原问题的最优单纯形表出发,适当修改后继续进行迭代以获得变化后的问题的最优解。若使用计算机求解,则可使用软件的编辑功能对模型进行修改,这里不再赘述。
例 8 是否生产新产品。
在第 2 章例 1 中,该厂除了生产产品A、 B外,还设计了一种新产品C。已知产品C的单位利润为 110 元;生产一单位产品C需使用劳动力 6 工时,设备 5 台时,消耗 7 千克原材料。问该厂是否应生产产品C和生产多少?
解:令 x 6 表示产品C的产量。根据题意,我们在最优单纯形表(见表3 -2)中增加变量 x 6 , x 6 的目标函数系数为 110, x 6 对应的列为:

x 6 对应的检验数 σ 6 = 110 -[0 × (-1.48)+ 70 × 0.6 + 120 × 0.52]= 5.6。
表 3 -4 是修改后的单纯形表,它是新问题的一个基可行解的单纯形表。
表 3 -4
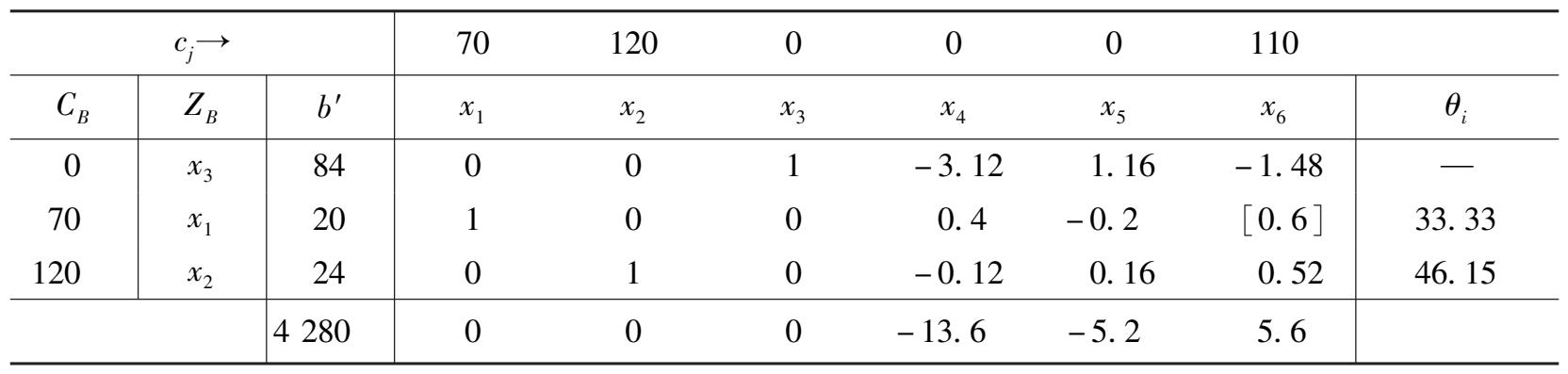
表 3 -4 不是最优表,经迭代后可获得新问题的最优单纯形表(见表 3 -5)。
由表 3 -5 可得新最优生产方案:生产产品B 6.667 单位,产品C 33.333 单位,不生产产品A。总利润为 4 466.667 元,比原计划增加了 186.667 元。
如果决策者只想知道新产品C是否应该投产,则从检验数 σ 6 > 0便可得出投产有利的结论(当然,要假设当前基最优解是非退化的)。
表 3 -5
