




迄今为止,当使用单纯形法解(SLP)时,我们总假定约束方程组已成为典式,这样能轻易找到一个初始基可行解并建立初始单纯形表。但一般来说,许多线性规划问题化为标准型后,其约束方程组的系数矩阵不一定含有 m 阶单位矩阵。这时,我们可以人为地添加一个或几个非负变量以构成单位矩阵,这样的变量称为人工变量。引入人工变量只是为了解题方便,为了不影响原问题的求解结果,要求运算结束后所有人工变量都取零值。使用下面介绍的大 M 法或两阶段法均可以达到这个目的。
1.大 M 法
大 M 法就是给目标函数中人工变量的系数赋值(- M ) ( M 是非常大的正数),这样,为了实现目标函数的最大化,单纯形法会自动使人工变量取零值。可以证明,若求解结果含有取正值的人工变量,则原问题无可行解。
例 7 用大 M 法解下列线性规划。
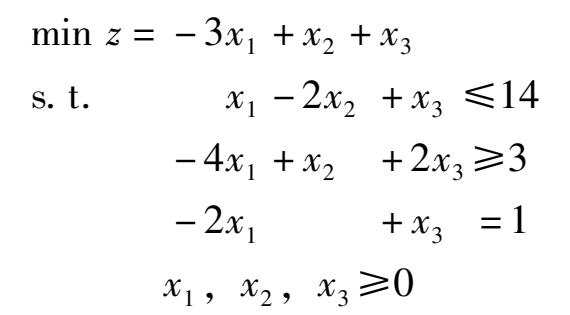
解:先把问题化为标准型
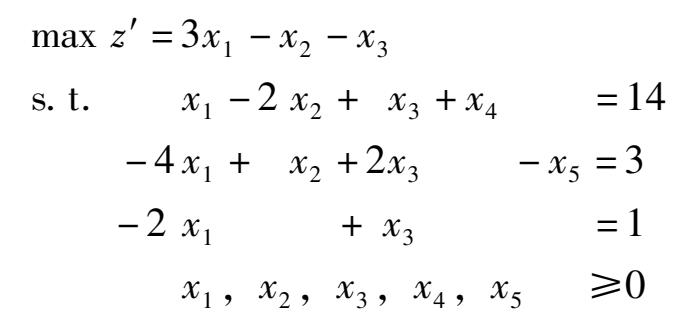
其中 x 4 为松弛变量, x 5 为剩余变量。
引入两个人工变量 x 6 , x 7 ,于是得到下面的大 M 问题:
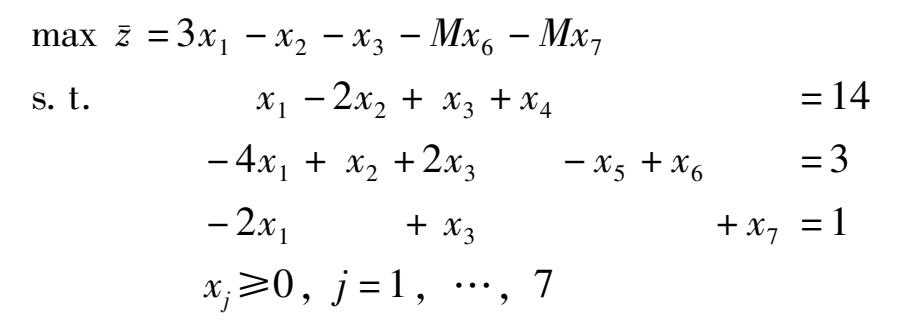
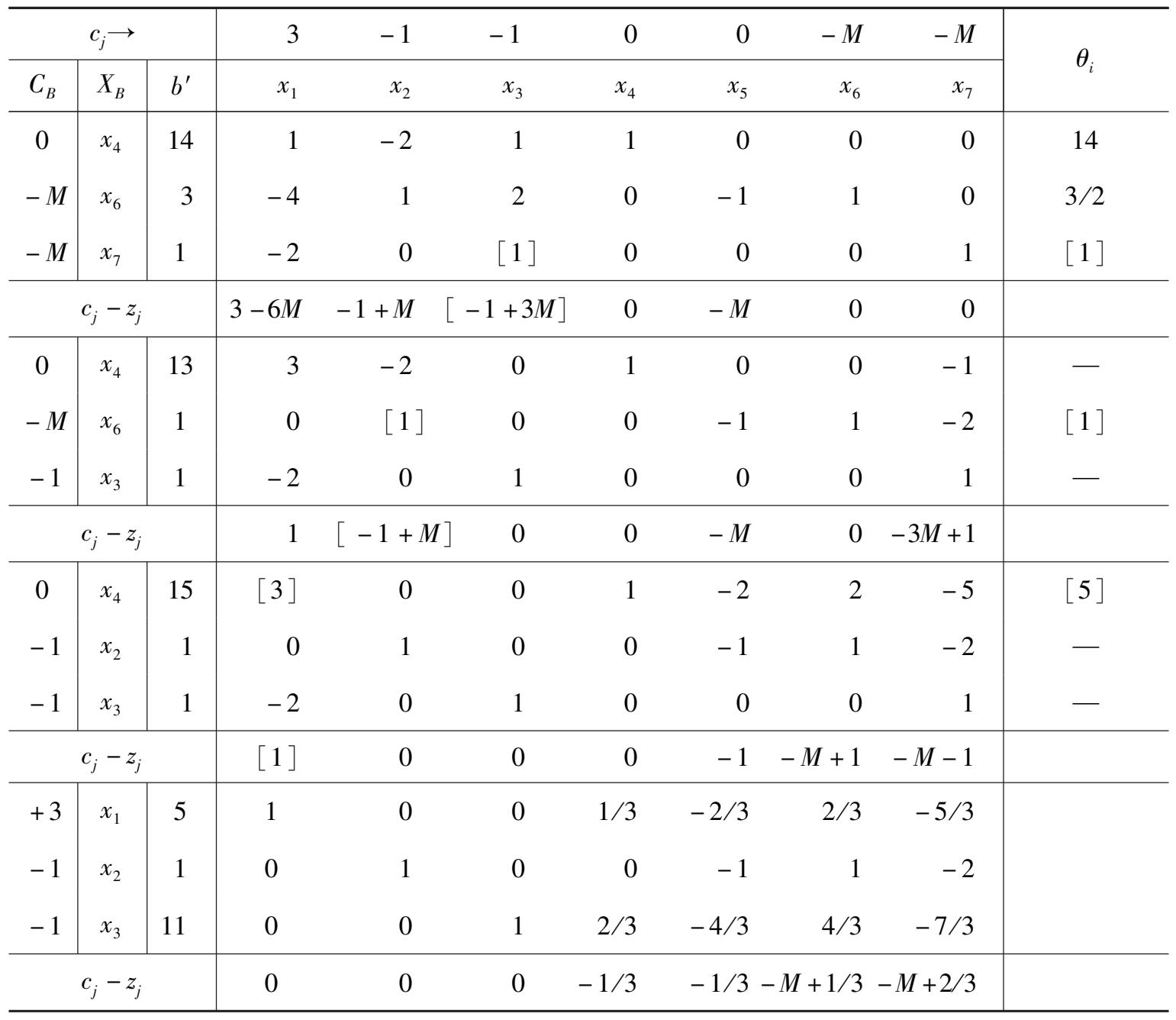
这里 M 是非常大的正数,计算时可认为它比任何可能出现的实数都要大。单纯形法迭代过程见表 2 -5。
表 2 -5 的最终表表明大 M 问题的最优解是(5,1,11,0,0,0,0) T ,最大值 z=3。因此,原问题的最优解是(5,1,11) T ,最小值 z = -3。
2.两阶段法
第一阶段:求出原问题的初始基可行解。具体做法是构造一个辅助线性规划,其目标函数 ω 是人工变量之和并要求实施最小化(人工变量非负,故等价于要求所有人工变量取零值),而约束方程组是已加入人工变量的典式。用单纯形法求解该辅助问题,若得到min ω = 0,表明所有人工变量都已取零值,第一阶段的最优解便是原问题的一个基可行解,可以进行第二阶段的计算;若min ω > 0,则原问题无可行解,应停止计算。
第二阶段:将第一阶段的最终表删去人工变量,并将目标函数行的系数换成原问题的目标函数系数,这就得到了第二阶段的初始单纯形表。下面举例说明两阶段法求解过程。
表 2 -5
例 8 用两阶段法求解例 7 的线性规划。
解:第一阶段的辅助问题(已转化为求max问题)为:
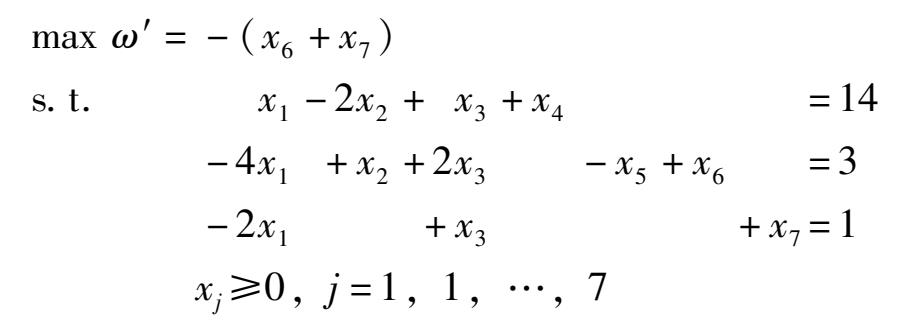
这里 x 6 、 x 7 是人工变量。表 2 -6 给出第一阶段的求解过程。求解结果是max ω′ = 0,得到的最优解是(0,1,1,15,0,0,0) T 。
表 2 -6
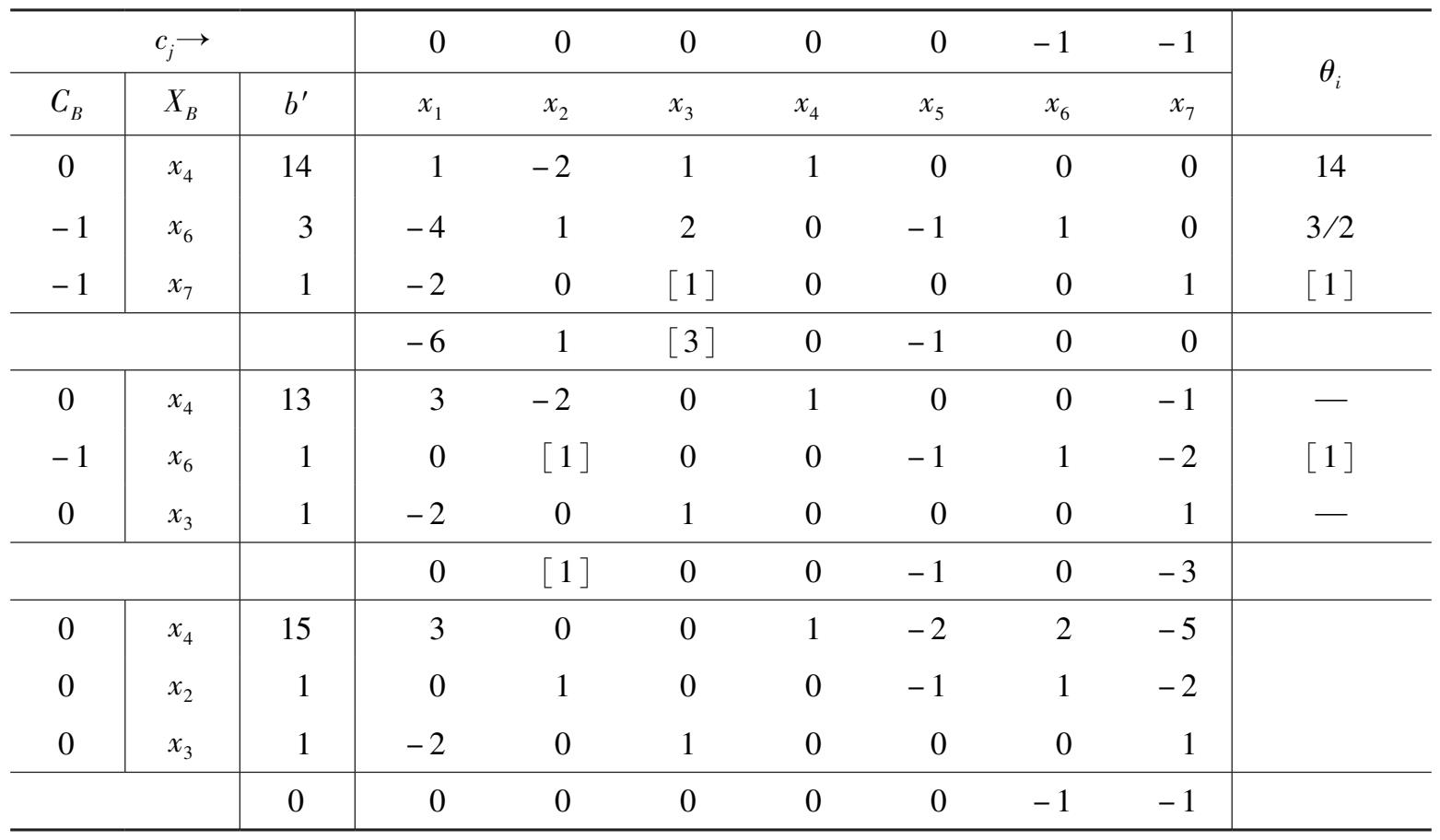
将第一阶段最终表中的人工变量删去,换回原问题的目标函数,进行第二阶段计算,过程如表 2 -7 所示。
表 2 -7
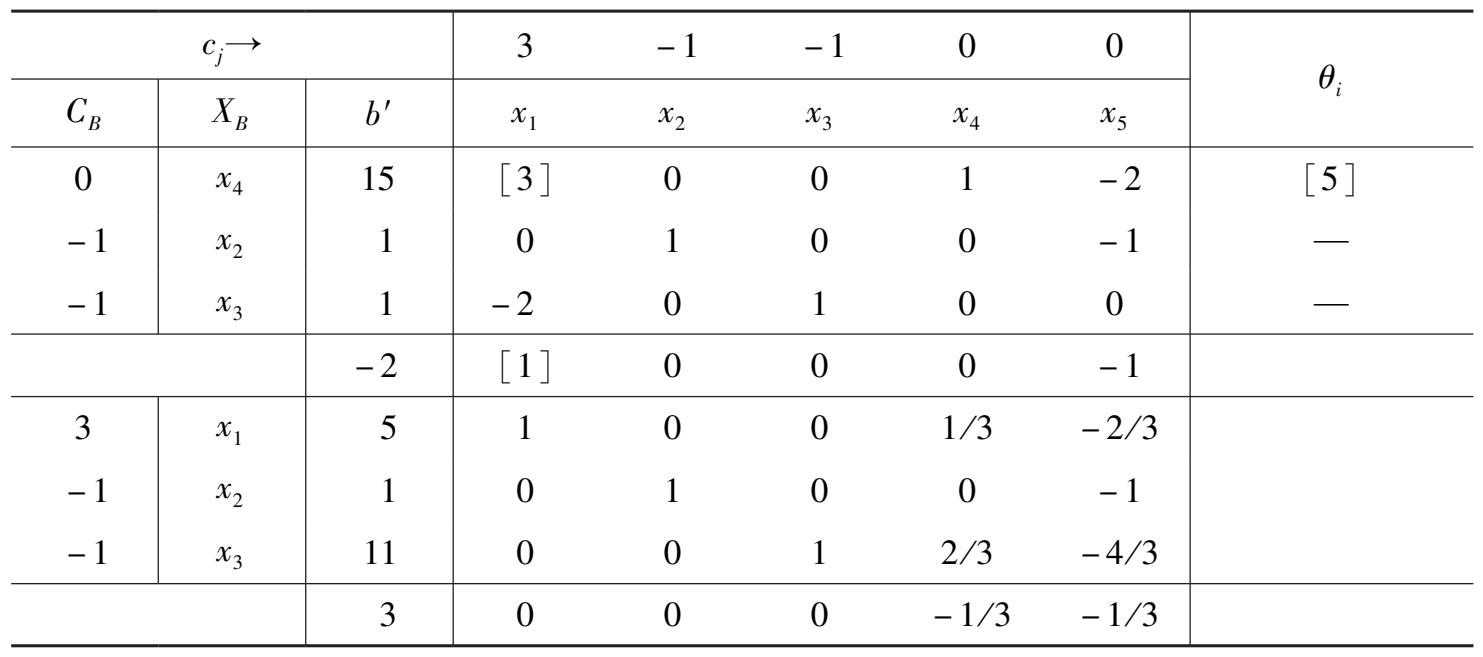
从表 2 -7 得到原问题的最优解为 x 1 = 5, x 2 = 1, x 3 = 11,最优值 z = -3。
事实上,对于标准化后的模型,增加资源向量后的增广矩阵为:

经过一系列的行变换后为:

得到的结果就是表 2 -7 中去掉人工变量后的结果。
线性规划有时存在多个最优解。使用最优单纯形表可以很容易地判断线性规划解的唯一性或求出它的另一些最优解。具体如下:
(1)当所有非基变量的检验数都小于零,则最优单纯形表给出的最优基可行解是唯一最优解。
(2)当存在某非基变量 x k 的检验数 σ k = 0,这时,并不能肯定线性规划一定有多个最优解,而要做进一步运算。我们可令 x k 入基,用 θ 规则(最小比值规则)确定出基变量。若 θ > 0,则旋转变换后可得到新最优基可行解,因此,问题有多个最优解;若 θ = 0,则进行旋转变换后,最优基可行解不变。
下面给出若干个说明例子。首先,由表 2 -7 可看出,最优单纯形表中非基变量的检验数都小于零,因此,例 9 的线性规划有唯一最优解。
例 9 设某线性规划问题的最优单纯形表如表 2 -8 所示,表中给出的最优基可行解 X ∗ = (4,2,0,0,4) T ,最优值 z ∗ = 24。
表 2 -8
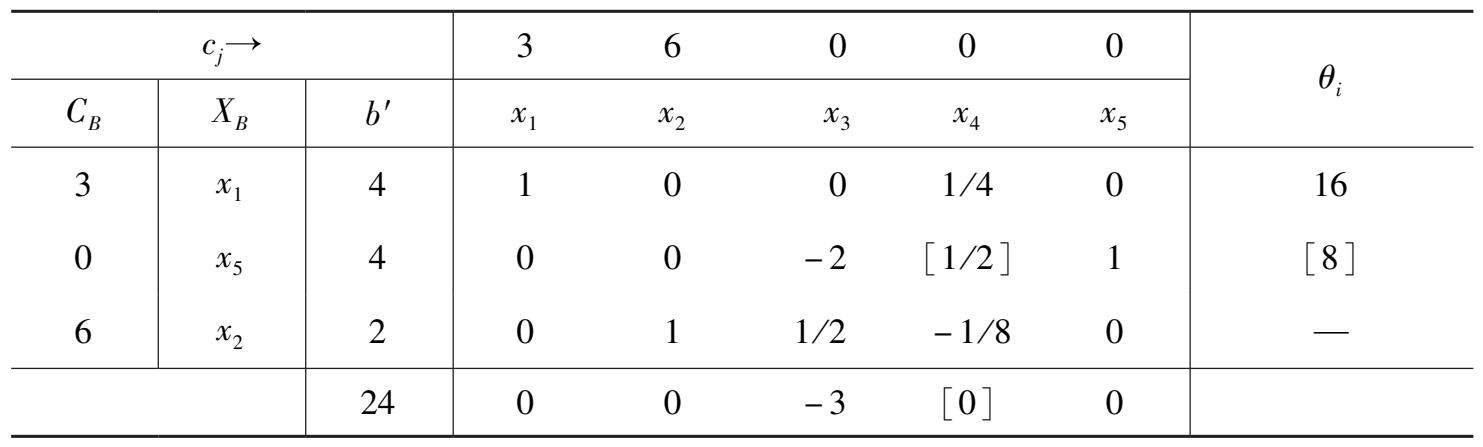
注意到表2 -8 中非基变量
x
4
的检验数为零,令
x
4
入基,用
θ
规则确定
x
5
为出基变量(这里
θ
= 8 > 0),旋转变换后可得表 2 -9。表 2 -9 给出另一个最优基可行解
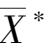 =(2,3,0,8,0)
T
,目标函数最优值仍为 24。
=(2,3,0,8,0)
T
,目标函数最优值仍为 24。
表 2 -9
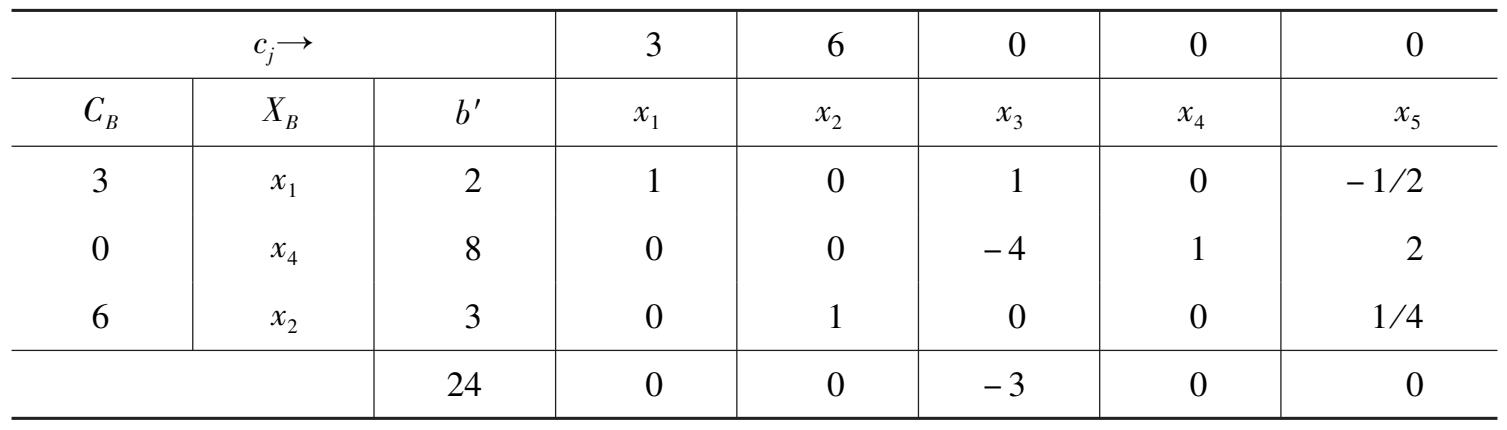
容易验证,对于 0≤
α
≤1,
X
=
αX
∗
+ (1 -
α
)
X
∗
也是问题的最优解,我们称
X
为
X
∗
与
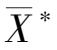 的凸组合(其几何意义是连接
X
∗
与
的凸组合(其几何意义是连接
X
∗
与
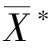 线段上的点)。这样的凸组合有无穷多个,因此,一个线性规划问题如果有两个不同的最优解,就有无穷多个最优解。
线段上的点)。这样的凸组合有无穷多个,因此,一个线性规划问题如果有两个不同的最优解,就有无穷多个最优解。
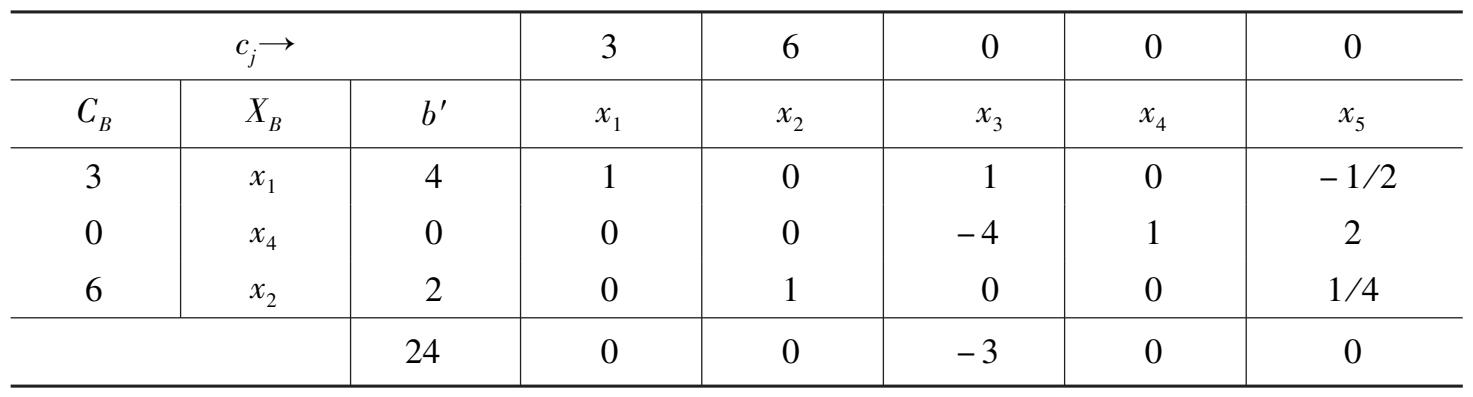
例 10 考察表 2 -10,表中给出了最优基可行解 X ∗ = (4,2,0,0,0) T ,最优值 z ∗ = 24。
表 2 -10

在表 2 -10 中,非基变量 x 4 的检验数为零,故令 x 4 入基,用 θ 规则可确定 x 5 为出基变量(此处 θ = 0),经过旋转变换后得表 2 -11,虽然最优基已经更换,但最优基可行解却保持不变。其实,不难看出此例的线性规划问题有唯一最优解。
表 2 -11
注:关于线性规划无穷多最优解的深入讨论,可参看参考文献 20。
前面已看到,在(SLP)非退化(即其所有的基可行解都非退化)的假设下,单纯形法每次迭代都使目标函数值严格增加,因此得到一个新的基可行解。因为基可行解的数目是有限的,所以迭代过程必在有限步后结束。
实际的线性规划问题普遍存在退化现象。退化现象有可能导致(尽管可能性微乎其微)“循环”现象:在迭代过程的某一阶段,某些可行基重复出现,而基可行解却不变。这样就破坏了单纯形法的有限步终止性,因此,有必要寻找避免循环的方法。历史上曾有人提出过几种方法,如“摄动法”“辞典序法”等,但规则都比较复杂。直到 1977 年Bland才提出和证明了一种实用的简单规则——最小下标规则:
(1)当有多个非基变量满足入基条件 σ k >0 时,则选择下标最小的变量入基。
(2)当使用 θ 规则确定出基变量,而有多个比值都等于 θ 时,则在所有满足出基条件的基变量中,选下标最小者出基。
若在计算过程中严格遵守Bland规则,可以证明一定不会发生基的循环,从而保证了单纯形算法的有限步终止性。
退化是常有的,而循环则极其罕见。截至目前,还没有发现实际问题中出现过循环现象,而只有为数极少的几个“人造”的循环例子。因此在实际计算上,人们往往不采取任何预防措施,以免增加计算程序的复杂性。