




本节将介绍信号失真及其测量,内容包括放大器失真、信号谐波失真和谐波失真测量。
如果一个输入信号在经过放大器后所产生的输出信号中包含其他频率分量的信号,就称为放大器的非线性。非线性是放大信号时最不希望看到的结果,由于非线性失真导致真实的信号所包含的信息发生了畸变,这将给后续的信号处理带来很大的困难。信号的失真表示如图1.2所示。
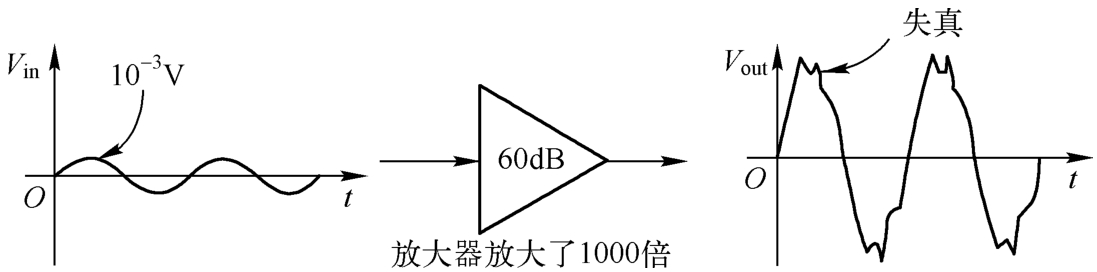
图1.2 信号的失真表示
从图1.2中可知,放大器是非线性的,实际的输出信号是输入信号与3次谐波信号的叠加,用下式表示:
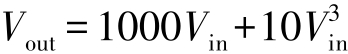
其与噪声不同,实际上是不可能消除失真的。因此,只能使用合适的器件将失真降到最低。
实际上,在大多数情况下很难准确确定放大器的非线性方程。如果知道了这个非线性方程,那么就可能消除或解决非线性问题。然而,即便是最简单的非线性,也很难消除。例如,考虑一个叠加二次谐波的系统:
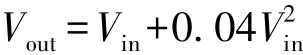
试着求解该方程,将 V in 表示为 V out 的函数。事实上,该方程没有唯一解。
非线性将会在数字信号处理中引起一系列的问题,如丢失或者屏蔽了想要的信号分量。在一定程度上,每个放大器都是非线性的。然而,如果在所感兴趣的信号频率范围内,非线性信号的功率非常小,则可以将放大器看作是线性的。在上面的例子里,非线性2次谐波分量占基波电压的1/5(功率的1/25),这是非常高的。因此,该放大器应看作是非线性的。根据系统的线性理论知识,也可以将系统划分为弱非线性、中度非线性或强非线性。
谐波失真是一种发生在输入信号频率谐波上的失真,其频率为输入信号频率的整数倍。如,一个1kHz的语音,谐波频率为2kHz,3kHz,4kHz,…
谐波产生的原因是器件的输入/输出电压特性呈现非线性特性,如它可以用二阶多项式表示:
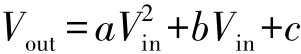
谐波失真是由非线性的传递函数产生的。如果假定传递函数是平稳的,如不随时间变化,而且输入信号呈现周期性,则输出也将是一个周期信号。在本小节你将看到,在频域内,周期信号的傅里叶级数由基波周期频率的谐波组成。因此,对于一个周期输入信号,无论 V in 和 V out 之间是怎样一种函数关系(只要不随时间变化),都不会出现非谐波失真。
对于输入信号:
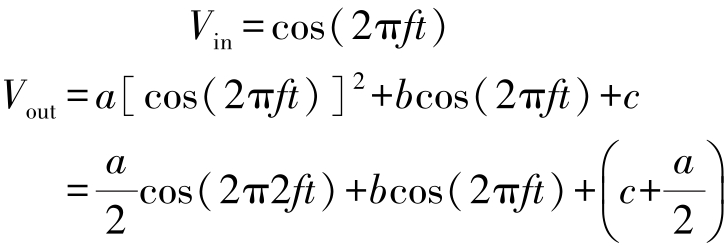
根据上式可以得到频率分量:
(1)cos(2π ft ):基波频率。
(2)cos(2π2 ft ):2次谐波。
V out 和 V in 之间更复杂的关系将导致更高次谐波,如那些大于2倍基频的频率。
对于放大器这样的器件,其常用指标是总谐波失真(Total Harmonic Distortion,THD),如图1.3所示。THD通常表示为谐波功率的和与基波功率之比,它是无量纲,用dB表示。
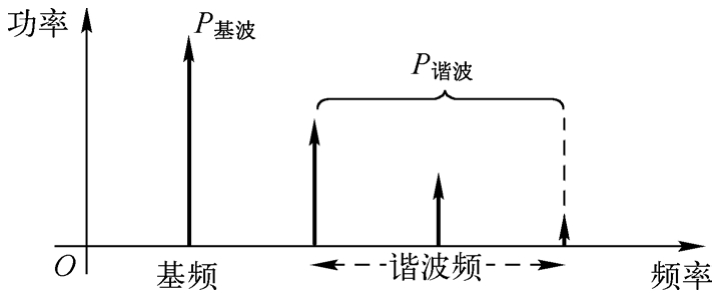
图1.3 THD的图形表示
THD可以用下式表示:
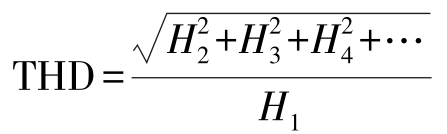
式中, H 1 表示基波功率, H 2 表示2次谐波分量, H 3 表示3次谐波分量……
注 :谐波的带宽选择是非常重要的,这是由于一些谐波序列可能有非常明显的高次谐波分量。
另一种常见的表示方法是THD+ N ,总谐波失真加上噪声,此处考虑输出噪声。在这种情况下,计算THD时用谐波功率总和加上噪声功率再除以基波功率。噪声功率是在输入为0的条件下测量的。