




描述方程式(1.4)的椭圆偏振光各参量之间关系的方法通常有琼斯矢量矩阵法、斯托克斯参量法、三角函数表示法和庞加莱球图示法。为了方便理解,这里仅介绍后面两种。
如图1.11所示,坐标系( x 'O y ')与( x O y )的转换矩阵为
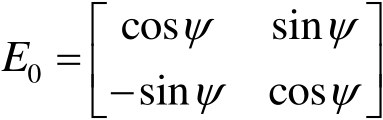
(1.9)
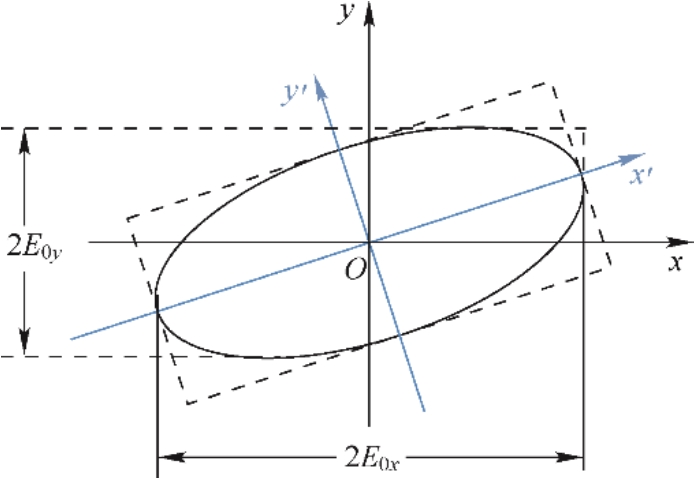
图1.11 椭圆偏振光各参数间的关系
而电场矢量在这两个坐标系之间的相互关系为
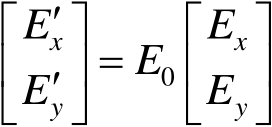
(1.10)
设2 a 和2 b 分别为椭圆的长轴和短轴,则( x ' Oy ')坐标系中椭圆的参量方程为
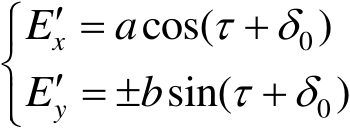
(1.11)
式中,正、负号分别对应于右旋和左旋椭圆偏振光。显然,由比值
 和角度
和角度
 两参量就可确定椭圆的外形及其在空间的取向,因此它们是椭圆偏振光的两个基本参量,同时也是实际工作中可以直接测量的两个量。下面再求它们和
两参量就可确定椭圆的外形及其在空间的取向,因此它们是椭圆偏振光的两个基本参量,同时也是实际工作中可以直接测量的两个量。下面再求它们和
 及其相位差
及其相位差
 的关系。为此,利用式(1.11)与式(1.10)的等价性可得
的关系。为此,利用式(1.11)与式(1.10)的等价性可得
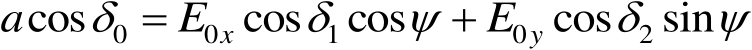
(1.12)
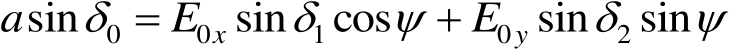
(1.13)
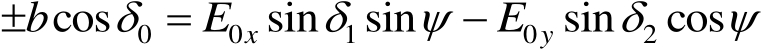
(1.14)
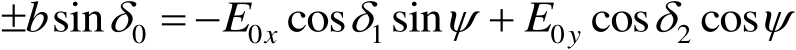
(1.15)
式(1.12)和式(1.13)平方相加,式(1.14)和式(1.15)平方相加,可得
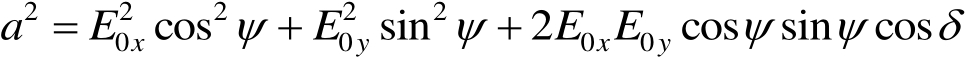
(1.16)
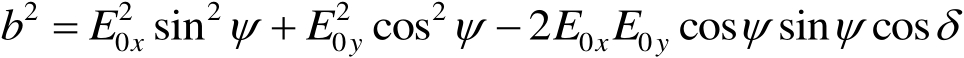
(1.17)
所以
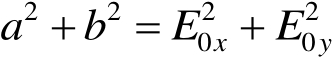
(1.18)
式(1.12)和式(1.14)相乘,式(1.13)和式(1.15)相乘,然后把两乘积相加,可得
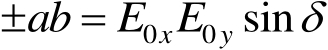
(1.19)
式(1.12)和式(1.14)相除,式(1.13)和式(1.15)相除,可得
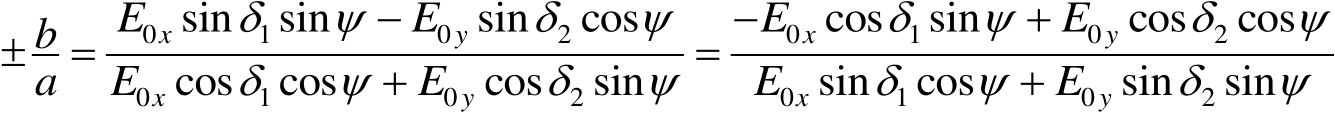
(1.20)
式(1.20)交叉相乘,则可求出
 的表达式:
的表达式:
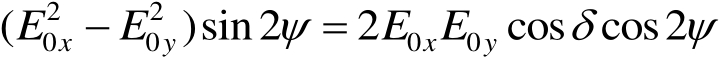
(1.21)
在实际测量中,比值
 较之
较之
 更为有用,且在计算上也更方便,故令
更为有用,且在计算上也更方便,故令
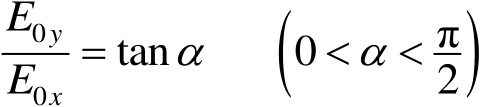
(1.22)
于是式(1.21)可简化成
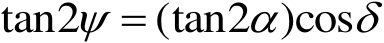
(1.23)
而由式(1.18)、式(1.19)可得
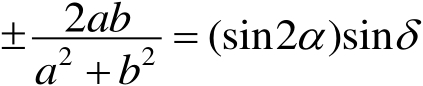
(1.24)
令
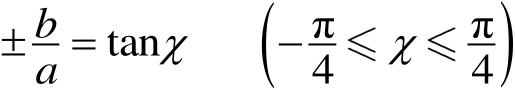
式中,正、负号分别表示椭圆是右旋还是左旋,于是式(1.24)可改写成
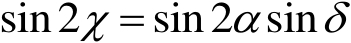
(1.25)
由此可见,若测出
 的实际值,则两偏振光的振幅
的实际值,则两偏振光的振幅
 及其相位差
δ
就可由下面的等式求出。
及其相位差
δ
就可由下面的等式求出。
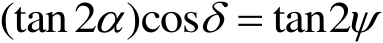
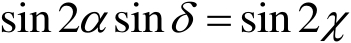
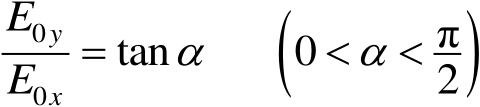
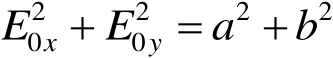
(1.26)
庞加莱球是表示任一偏振态的图示法,是1892年由H.Poincare(庞加莱)提出来的。由于任一椭圆偏振光只需要两个方位角就可以完全决定其偏振态,而两个方位角可以用球面上的经度和纬度来表示,因此球面上一个点就可以代表一个偏振态。球面上的点,就是各种偏振态的组合。
1.斯托克斯参量描述
任一平面单面光波的偏振态可用两个相互垂直的振动来表示。如以 xOy 表示其振动平面,则这两个振动可表为
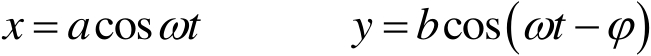
(1.27)
式中,
 为该单色光的角频率;
为该单色光的角频率;
 和
和
 分别为在振动平面内沿
分别为在振动平面内沿
 和
和
 方向的振幅;
方向的振幅;
 为
a
、
b
间的相位差。正是这3个相互独立的常量
为
a
、
b
间的相位差。正是这3个相互独立的常量
 共同描述着该光波的偏振态。但是,我们也可以不用它们,而用Stokes参量来描述其偏振态。Stokes参量共有4个,它们是
共同描述着该光波的偏振态。但是,我们也可以不用它们,而用Stokes参量来描述其偏振态。Stokes参量共有4个,它们是
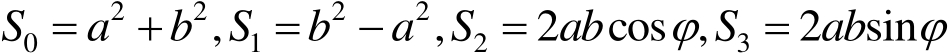
(1.28)
注意,这4个量中只有3个是独立的。因为,无论
 为何值,这4个量总存在着一个关系:
为何值,这4个量总存在着一个关系:
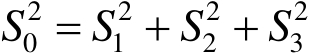
(1.29)
而其中
 的平方表示该光波振动的强度。
的平方表示该光波振动的强度。
根据式(1.28)和式(1.29),我们可以引入这样一个三维空间,它由相互垂直的空间轴
 、
、
 和
和
 所构成。在这个空间里,对任一已知强度(
所构成。在这个空间里,对任一已知强度(
 一定)的单色光波都可作一球面:球心在原点,半径为
一定)的单色光波都可作一球面:球心在原点,半径为
 。这样一来,该球面上的任意一点
M
就表示该光波的一个特定的偏振态。由图1.12中可看出,球面上任一点
M
的坐标
。这样一来,该球面上的任意一点
M
就表示该光波的一个特定的偏振态。由图1.12中可看出,球面上任一点
M
的坐标
 、
、
 和
和
 分别与
分别与
 、
、
 和
和
 有如下关系:
有如下关系:
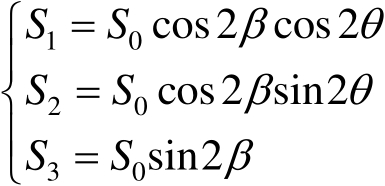
(1.30)
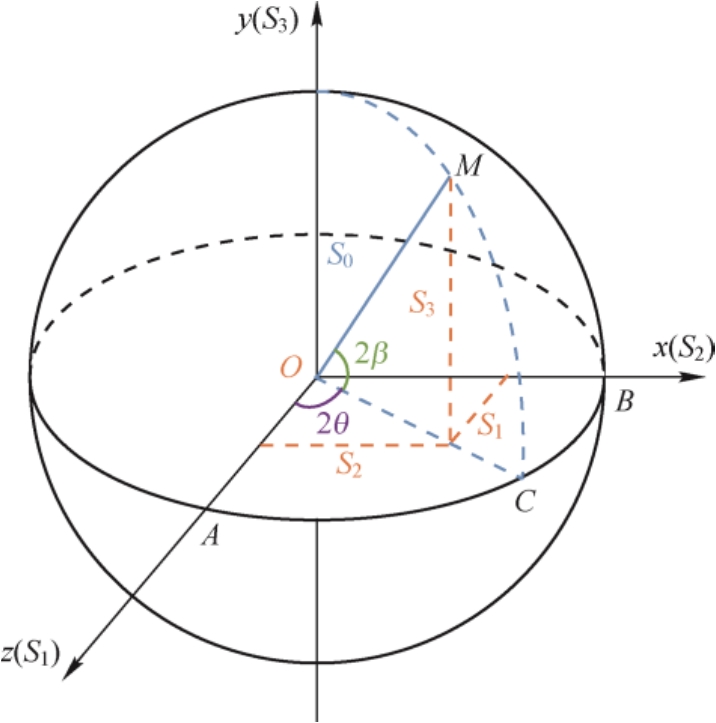
图1.12 庞加莱球上任意一点的偏振态表示方法
如上定义并用来描述特定强度的单色光波的偏振态的这种球面就是庞加莱球(Poincare球)。
2.庞加莱球特征
由上述定义和球面三角学的基本公式可以证明庞加莱球具有如下的特征:
①庞加莱球赤道上的不同点表示振动方向不同的线偏振光,如图1.13所示。因为在这些点上
 ,即
a
=0或
b
=0,或
,即
a
=0或
b
=0,或
 ,其中
k
只能为零或任一整数。在
Os
1
轴与球面的交点
A
处,
,其中
k
只能为零或任一整数。在
Os
1
轴与球面的交点
A
处,
 也为零,有
也为零,有
 ,因此
,因此
 ,即点
A
表示平行于
,即点
A
表示平行于
 (
Os
3
)的线偏振态。同理,在
Os
2
轴与球面的交点
B
处,由式(1.28)可知它表示与
(
Os
3
)的线偏振态。同理,在
Os
2
轴与球面的交点
B
处,由式(1.28)可知它表示与
 (
Os
3
)成45°的线偏振态。与点
A
通过球心在球面上对应的点
A
′表示与
(
Os
3
)成45°的线偏振态。与点
A
通过球心在球面上对应的点
A
′表示与
 (
Os
3
)成90°即与
(
Os
3
)成90°即与
 (
Os
2
)方向平行的线偏振态。不难直接证明:在赤道上与
(
Os
2
)方向平行的线偏振态。不难直接证明:在赤道上与
 对应的任一点
C
表示与
对应的任一点
C
表示与
 (
Os
3
)成
(
Os
3
)成
 角的线偏振态。
角的线偏振态。
②庞加莱球的两极
P
和
P
′分别表示左旋和右旋圆偏振态。因为在这两点处
 ,则有
,则有
 和
和
 。对于
P
点,
。对于
P
点,
 ,
k
为零或偶数;对于
P
′点,
,
k
为零或偶数;对于
P
′点,
 ,
k
为奇数。
,
k
为奇数。
③庞加莱球上任一确定点
 (
(
 ),由于
),由于
 和
和
 和
和
 都确定,因而
都确定,因而
 也确定。所以,一确定的点
也确定。所以,一确定的点
 表示一确定的椭圆偏振态。两极和赤道除外,由式(1.28)和(1.30)可以得到
表示一确定的椭圆偏振态。两极和赤道除外,由式(1.28)和(1.30)可以得到
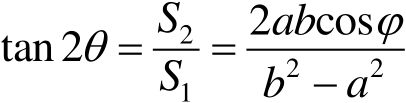
(1.31)
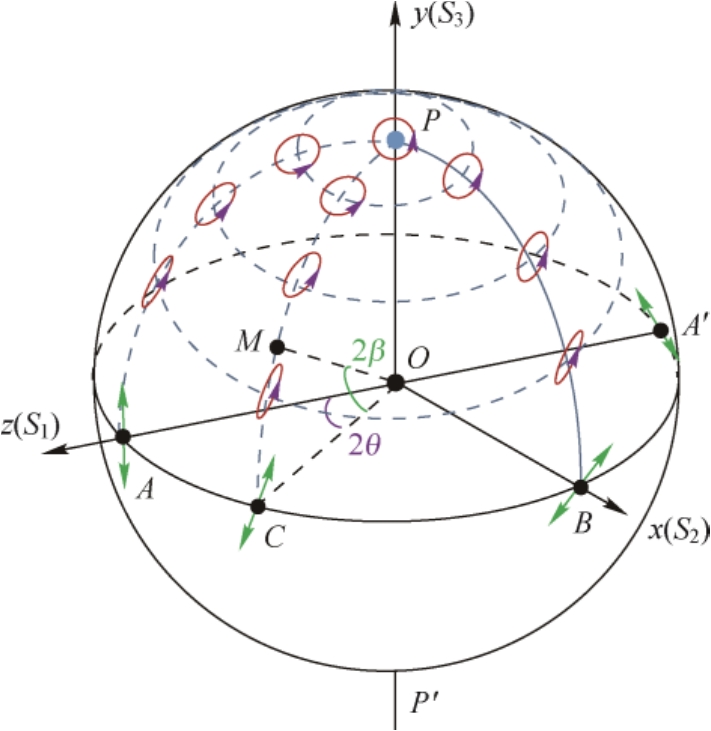
图1.13 庞加莱球赤道上点的线偏振态
 正是当
正是当
 确定时,由式(1.28)表示的由两相互垂直振动所合成的椭圆振动的主轴与
确定时,由式(1.28)表示的由两相互垂直振动所合成的椭圆振动的主轴与
 方向的夹角。又由于在庞加莱球同一经线上的各点有相同的
方向的夹角。又由于在庞加莱球同一经线上的各点有相同的
 ,所以这些点表示不同的椭圆偏振态,但这些椭圆的主轴有相同的取向,它们的主轴都与
,所以这些点表示不同的椭圆偏振态,但这些椭圆的主轴有相同的取向,它们的主轴都与
 成
成
 角。由式(1.28)和(1.30)也可以得到
角。由式(1.28)和(1.30)也可以得到

(1.32)
 的正切是当
的正切是当
 确定时,由式(1.28)表示的由两相互垂直振动所合成的椭圆振动的轴比。因此,庞加莱球同一纬度线上的各点(有相同的
确定时,由式(1.28)表示的由两相互垂直振动所合成的椭圆振动的轴比。因此,庞加莱球同一纬度线上的各点(有相同的
 )表示不同的椭圆偏振态,且这些椭圆具有相同的轴比,或者说具有相同的偏心率,如图1.13所示。由式(1.28)和式(1.30)还可以得到
)表示不同的椭圆偏振态,且这些椭圆具有相同的轴比,或者说具有相同的偏心率,如图1.13所示。由式(1.28)和式(1.30)还可以得到

(1.33)
另一方面,将球面三角学的基本公式用于庞加莱球面上的直角三角形
 (见图1.14),可以得到
(见图1.14),可以得到

(1.34)
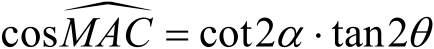
(1.35)
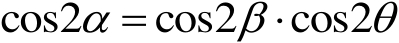
(1.36)
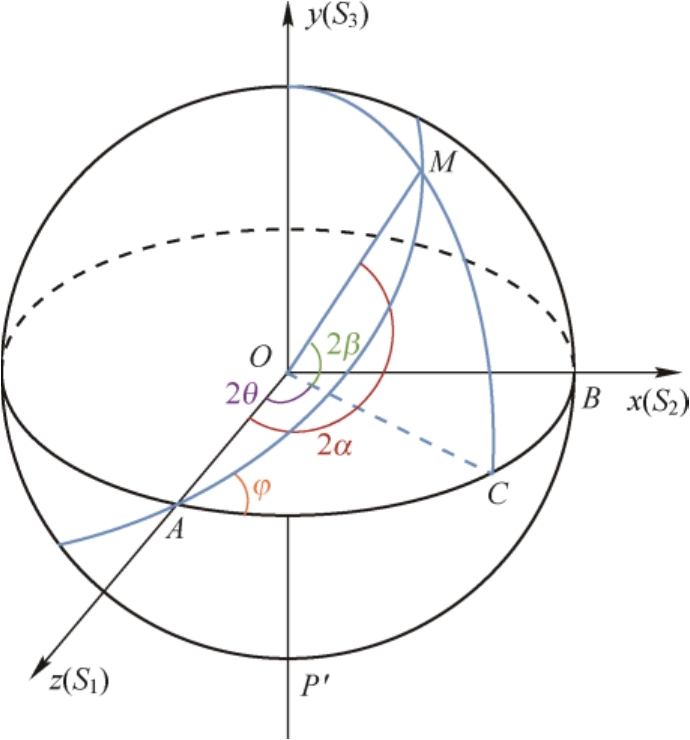
图1.14 庞加莱球上椭圆偏振光的相位差
由这三个式子消去
 ,得到
,得到
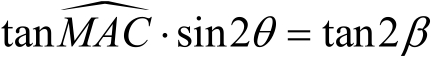
(1.37)
比较式(1.33)和式(1.37),可知
 ,即证明了在庞加莱球面上的角
,即证明了在庞加莱球面上的角
 就是构成
就是构成
 点所表示的椭圆偏振态在
点所表示的椭圆偏振态在
 和
和
 方向的两个振动分量的相位差
方向的两个振动分量的相位差
 。
。
又由于对北半球的各点
 ,
,
 满足:
满足:

即
 方向的振动都超前于
方向的振动都超前于
 方向的振动,故它们所表示的各椭圆偏振态都是左旋的;相反,在南半球的各点
方向的振动,故它们所表示的各椭圆偏振态都是左旋的;相反,在南半球的各点
 所表示的各椭圆偏振态都是右旋的(见图1.13)。
所表示的各椭圆偏振态都是右旋的(见图1.13)。
④可以证明在庞加莱球上的
 仅与
仅与
 有如下关系:
有如下关系:
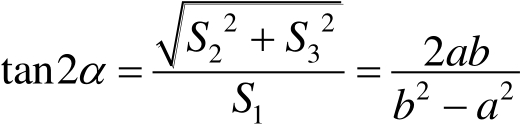
(1.38)
而与
 无关。
无关。
注意:当
 点不在赤道上时,它所表示的椭圆偏振的主轴与
点不在赤道上时,它所表示的椭圆偏振的主轴与
 夹角由式(1.31)中的
夹角由式(1.31)中的
 所确定。在这些点上,由于
所确定。在这些点上,由于
 ,一般来说
,一般来说
 。只有当
。只有当
 (即
(即
 )时,或
M
点在赤道上(
)时,或
M
点在赤道上(
 )时才有
)时才有
 。
。