




本节介绍堆排序的原理和具体实现方法。
堆排序(Heap Sort)是一种基于二叉堆数据结构和比较的排序技术。它类似于选择排序,即首先找到最小元素并将最小元素放在开头,然后对其余元素重复相同的过程。
那什么是二叉堆(Binaryheap)呢?首先,定义一个完全二叉树。完全二叉树是一种二叉树,除可能的最后一层外,其余的每一层都被完全填满,并且所有节点都尽可能靠左。二叉堆是一个完全二叉树,以特殊顺序存储,使得父节点中的值大于/小于其两个子节点中的值。前者称为最大堆,如图1.84(a)所示;后者称为最小堆,如图1.84(b)所示。堆可以用二叉树或数组表示。
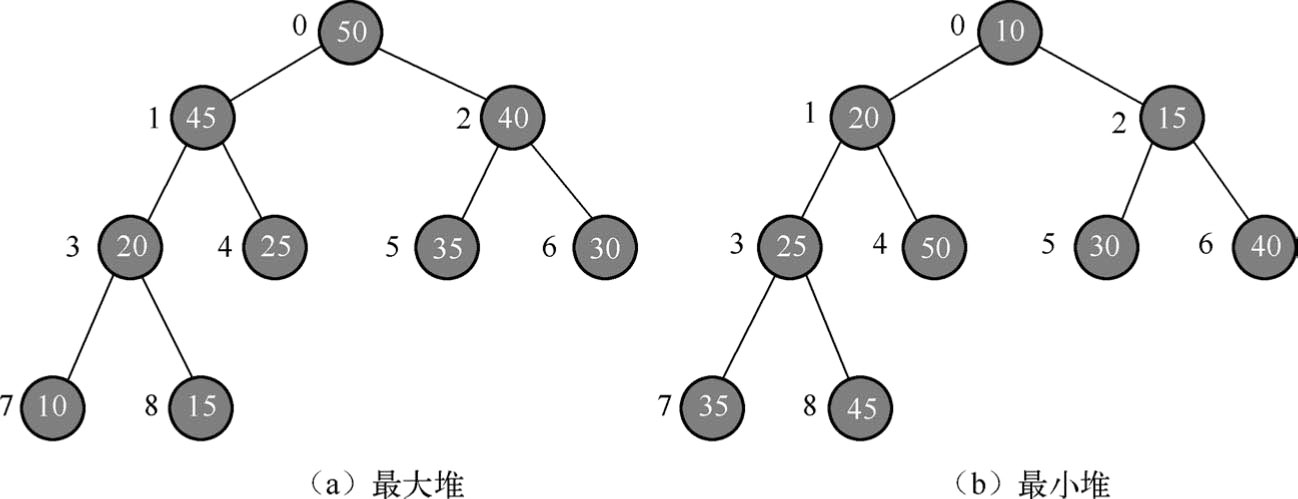
图1.84 二叉堆之最大堆和最小堆
为什么用数组来表示二叉堆?这是因为二叉堆是一颗完全二叉树,它可以很容易地表示为一个数组,并且基于数组的表示可以节省空间。如果父节点保存在索引 i 处,则左孩子可以通过2× i +1计算,右孩子可以通过2× i +2计算(假设索引从0开始)。
对于图1.84(a)中的最大堆来说,用数组arr表示为
arr[9]={50,45,40,20,25,35,30,10,15}
该数组从逻辑上讲就是一个堆结构,且满足:
arr[ i ]≤arr[2× i +1] 且 arr[ i ]≤arr[2× i +2]
类似地,对于图1.84(b)中的最小堆来说,用数组arr表示为
arr[9]={10,20,15,25,50,30,40,35,45}
该数组从逻辑上讲就是一个堆结构,且满足:
arr[ i ]≥arr[2× i +1] 且 arr[ i ] ≥arr[2× i +2]
如何“堆”一颗树?将二叉树重塑为堆数据结构的过程称为“堆化”。二叉树是一种树数据结构,最多有两个子节点。如果一个节点的子节点为“已经堆化”的,则只能在该节点上应用“堆化”过程。
从一棵完整的二叉树开始,可以通过在堆的所有非叶子元素上运行一个名字为“堆化”(heapify)的函数将其修改为最大堆(Max-Heap),即“堆化”使用递归。
图1.85所示为“堆化”的一个例子。在图1.85中,由于孩子[70(1)]比父亲[30(0)]大,因此将孩子[70(1)]和父亲[30(0)]进行交换,如图1.85(b)所示。
堆排序的基本思想是:将待排序序列构造成一个最大堆。此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾数据就是最大值。然后将剩余的 n -1个元素重新构造一个堆,这样会得到 n 个元素的次小值。如此反复执行,便能得到一个有序序列。
下面通过一个例子来说明这个问题。
(1)假设给定一个未排序的初始的数组arr[5],其数据元素表示为
arr[5]={4,6,8,5,9}
使用二叉树表示该无序数组元素,如图1.86所示。
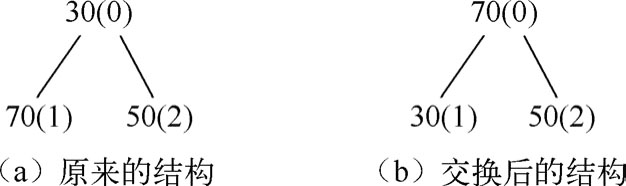
图1.85 一个“堆化”的结构
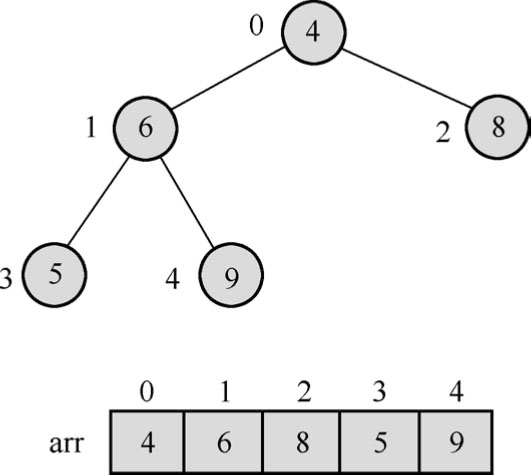
图1.86 无序数据序列的完备二叉树表示
(2)从最后一个非叶子节点开始(叶子节点不用调整,第一个非叶子节点坐标为数组长度/2-1=5/2-1=1,即是下面的节点1,其内容为6),从左至右,从下至上进行调整,如图1.87所示。
在将数据元素6和数据元素9比较交换之后,必须考虑内容为9的这个节点对于其子节点会不会产生任何影响?由于它是叶子节点,因此不用考虑这个问题。
(3)找到第二个非叶子节点0(该节点的内容为4)。因为在3个数据元素4、9和8中,数据元素9最大,因此将数据元素4和数据元素9进行交换,如图1.88所示。
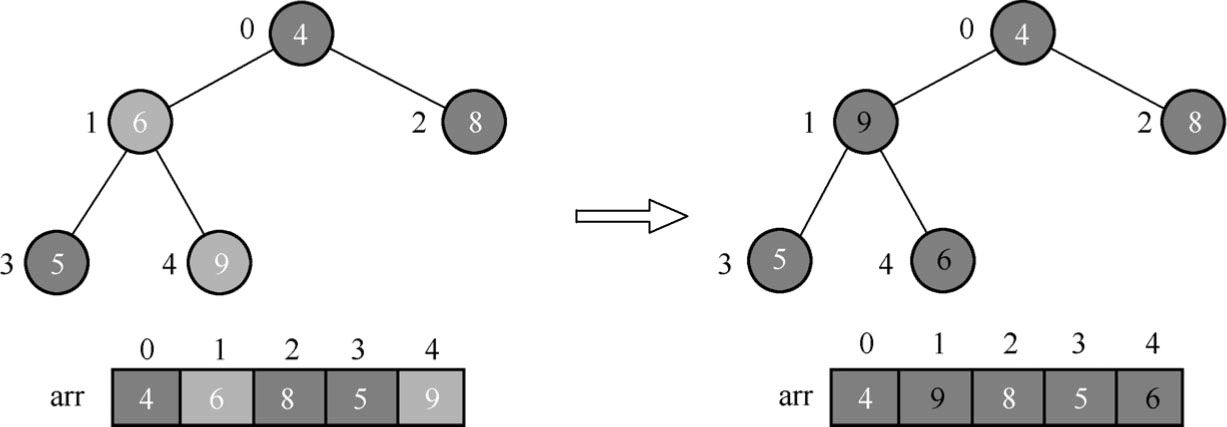
图1.87 调整节点位置(1)
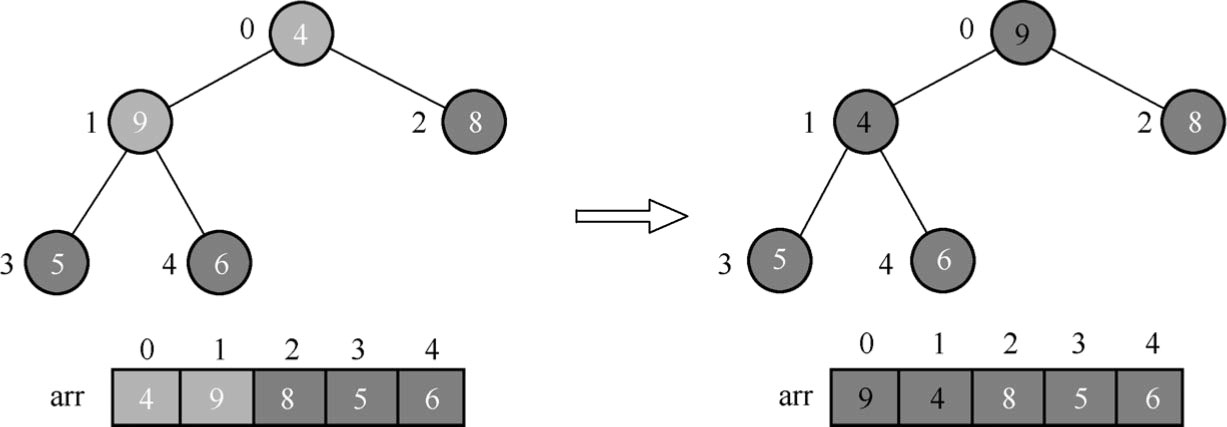
图1.88 调整节点位置(2)
此时,数据元素4和数据元素9交换过后,必须考虑原先内容为9的节点1的位置,因为该节点的值变为了4,需要重新判断以节点1作为根节点的那棵子树是否还满足最大堆的原则,每一次交换,都必须循环将子树部分判别清楚。
(4)由于前面的交换导致了子树的3个数据元素4、5和6的结构混乱。按照最大堆规则继续调整树的节点。因为在3个数据元素4、5和6中,数据元素6的值最大,因此交换数据元素4和数据元素6,如图1.89所示。
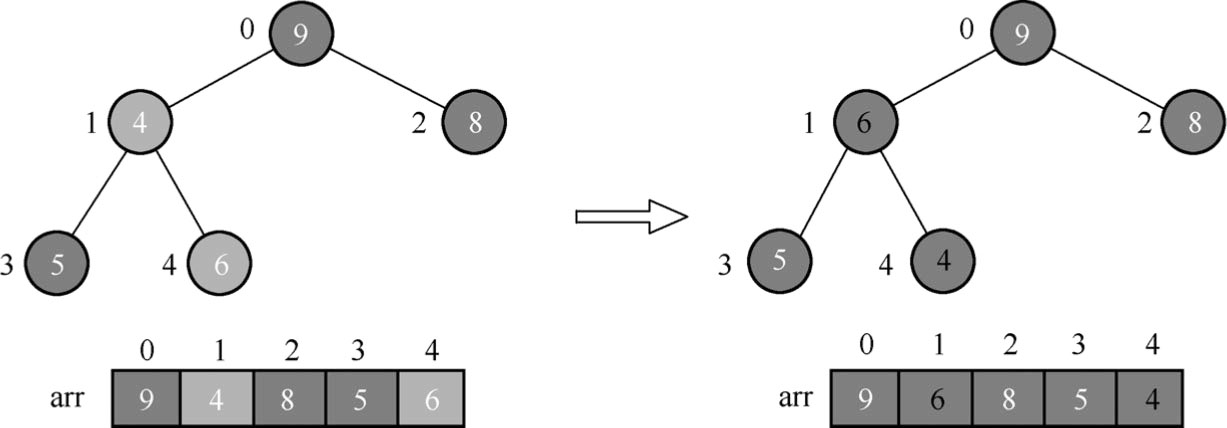
图1.89 调整节点位置(3)
牢记上面所说的规则,每次交换都要将改变了的那个节点所在的树重新判定一下,必须重新调整变动了的那棵子树,一直到符合最大堆的规则为止。
此时,就将一个无序的数据序列构造成了一个最大堆结构。
(5)将堆顶元素与末尾元素进行交换,使末尾元素最大,如图1.90所示。将堆顶数据元素9和末尾数据元素4进行交换。
此处,需要强调一下,所谓的“交换”,实际上就是从树里面将最大值拿掉,剩余的其他元素参与到排序的树,所以图1.90中使用虚线表示。
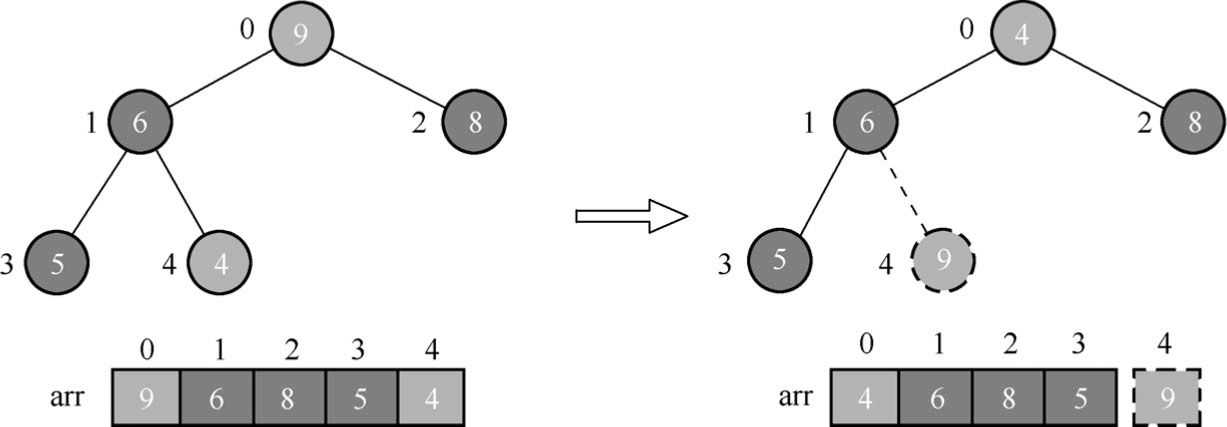
图1.90 调整节点位置(4)
(6)继续调整最大堆,如图1.91所示。图1.91中,调整节点0和节点2中数据元素4和数据元素8的位置。
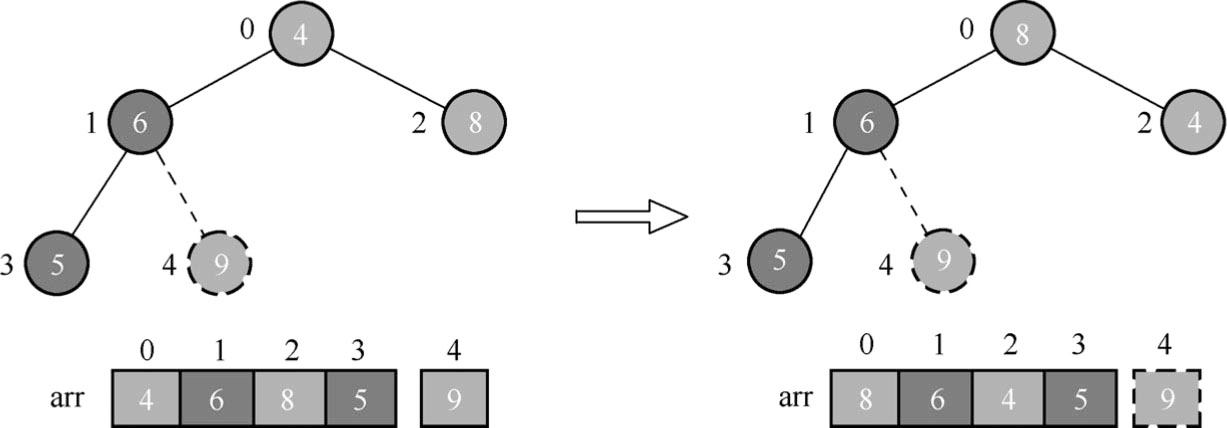
图1.91 调整节点位置(5)
(7)继续调整最大堆,如图1.92所示。将堆顶数据元素8与末尾数据元素5进行交换,得到排序中的第二大数据元素8。
(8)后续过程,继续进行调整、交换,如此反复,直到完成排序过程,如图1.93所示。
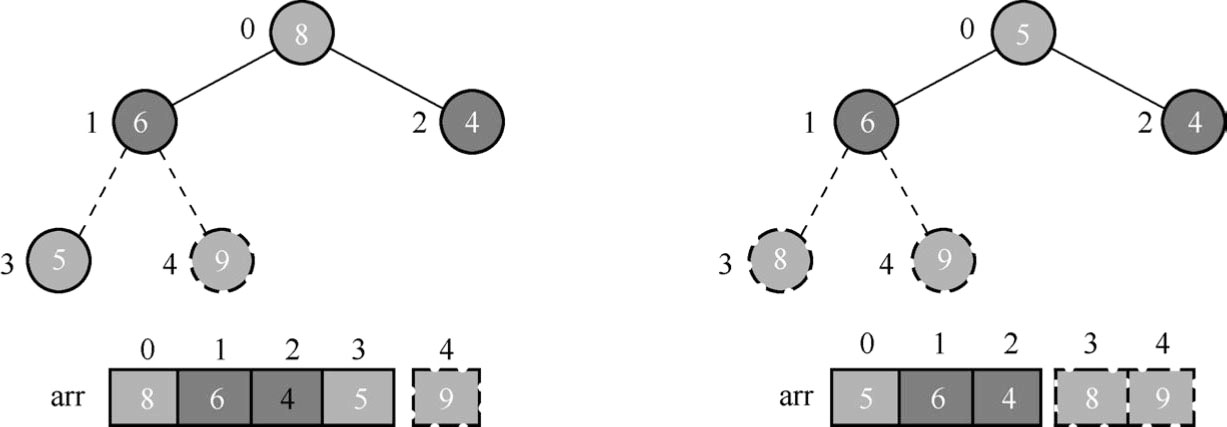
图1.92 调整节点位置(6)
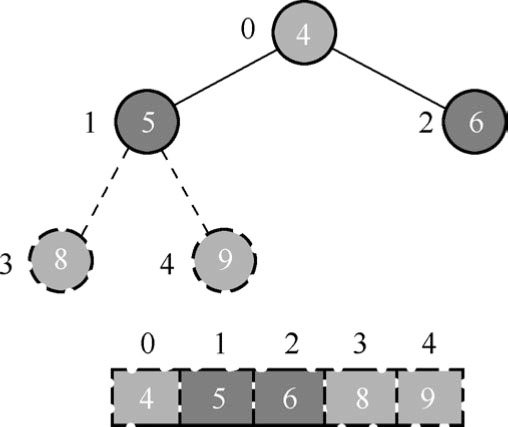
图1.93 调整完成后的最终结构
实现堆排序算法的C语言代码如代码清单1-14所示。

代码清单1-14 实现堆排序算法的C语言代码


注 :读者可以定位到本书提供资源的\loongson1B_training_example\example_1_14目录中,使用LoongIDE软件工具打开example_1_14.lxp工程文件。
本节将介绍如何对设计工程进行编译,并通过调试器对C语言设计代码进行调试。具体实现步骤如下所示。
(1)编译程序代码,给龙芯1B硬件开发平台上电。
(2)如图1.94所示,在代码清单1-14中设置第一个断点。

图1.94 在代码清单1-14中设置第一个断点
(3)如图1.95所示,在代码清单1-14中设置第二个断点。

图1.95 在代码清单1-14中设置第二个断点
(4)在LoongIDE主界面主菜单下,选择Debug->Run,程序停在第一个断点处。
(5)在调试器界面中,单击“Watchs”标签。在该标签页中,单击鼠标右键,出现浮动菜单。在浮动菜单内,选择Add Watch,弹出“Add Variable Watch”对话框。
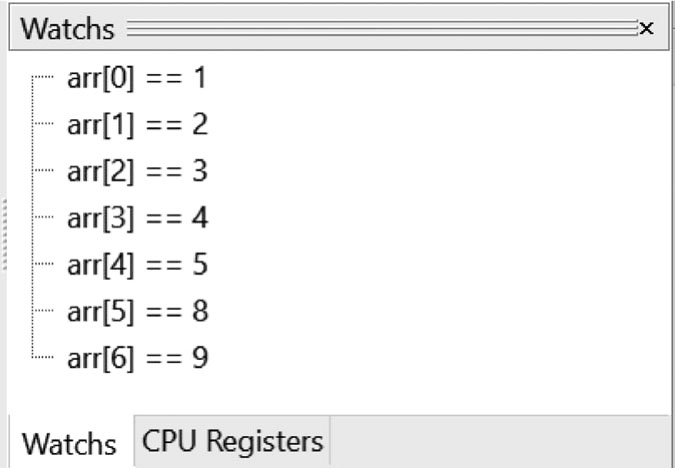
图1.96 “Watchs”标签页
(6)在“Add Variable Watch”对话框中的文本框中输入“arr[0]”,单击“OK”按钮,退出该对话框。
(7)重复步骤(5)和(6),再添加6个变量,即arr[1]、arr[2]、arr[3]、arr[4]、arr[5]和arr[6]。
(8)在LoongIDE主界面主菜单下,选择Debug->Run,程序停在第二个断点处。
(9)单击“Watchs”标签,即可看到如图1.96所示的“Watchs”标签页。
实现堆排序算法的汇编语言代码如代码清单1-15所示。

代码清单1-15 实现堆排序算法的汇编语言代码



注 :读者可以定位到本书提供资源的\loongson1B_training_example\example_1_15目录中,使用LoongIDE软件工具打开example_1_15.lxp工程文件。
本节将介绍如何对前面所设计的汇编语言代码进行编译,并在龙芯1B硬件开发平台上进行调试和验证。具体实现步骤如下所示。
(1)编译程序代码,给龙芯1B硬件开发平台上电。
(2)如图1.97所示,在代码清单1-15中处设置第一个断点。

图1.97 在代码清单1-15中设置第一个断点
(3)如图1.98所示,在代码清单1-15中设置第二个断点。

图1.98 在代码清单1-15中设置第二个断点
(4)在LoongIDE主界面主菜单下,选择Debug->Run,进入调试器界面,程序自动停到第一个断点处。
(5)单击“CPU Registers”标签,在CPU Registers标签页中,找到寄存器名字为“s0”的一行,并用鼠标左键双击该行,弹出“View Memory”对话框,如图1.99所示。在图1.99 中可以看出,用于存放数据段中名字为“arr”的存储空间的首地址为0x80212668。
(6)在“View Memory”对话框中,按如下设置参数。
① Count:14(通过“Count”右侧的旋转旋钮设置)。
② 单击“Fetch”按钮。
在“View Memory”对话框中显示了从0x80212668地址开始的7个要排序的数据,即0x0003、0x0004、0x0002、0x0008、0x0009、0x0005和0x0001。
(7)单击图1.107中的按钮图标
 ,退出“View Memory”对话框。
,退出“View Memory”对话框。
(8)在LoongIDE主界面主菜单下,选择Debug->Run,程序停在第二个断点处。
(9)单击“CPU Registers”标签,在“CPU Registers”标签页中,找到寄存器名字为“s0”的一行,并用鼠标左键双击该行,弹出“View Memory”对话框,如图1.100所示。在图1.100中可以看出,用于存放数据段中名字为“arr”的存储空间的首地址为0x80212668,同时也可看到从该地址开始的7个已经排完序的数据,即0x0001、0x0002、0x0003、0x0004、0x0005、0x0008和0x0009。
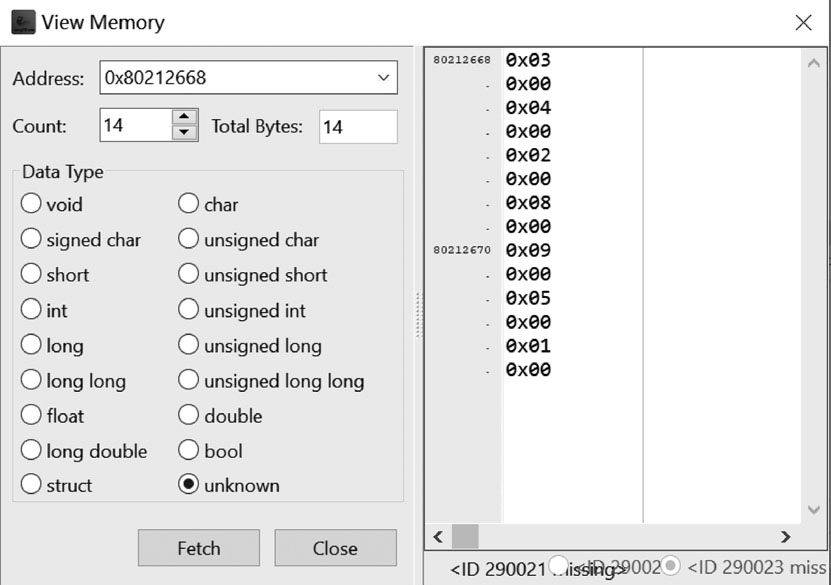
图1.99 “View Memory”对话框(1)
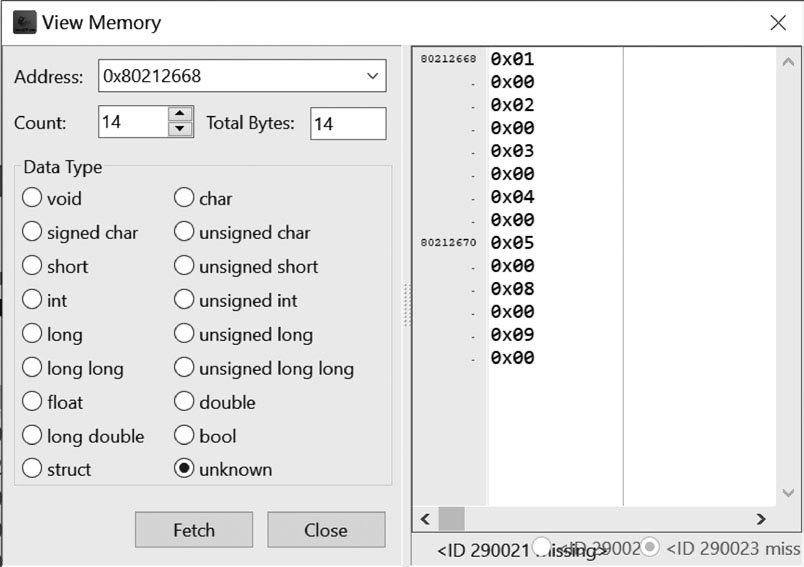
图1.100 View Memory对话框(2)