




为了提升系统任务可靠性,可在不关机的情形下直接维修或替换发生故障的单元、组件。对于在线维修系统和定期检修系统等可修系统,主要的可靠性指标包括系统首次故障时间分布、可用度(包括稳态可用度和瞬时可用度)、可靠度、(0, t ]中系统的平均故障次数(故障频度)、系统平均故障间隔时间等。不同领域产品对可靠性指标关注的侧重点有所不同,上述指标则从各个方面反映了可修系统的可靠性。可修系统的可靠性数量指标,如图3-24所示。

图3-24可修系统示意图
首次故障前平均时间(记为MTTFF):

平均开工时间(记为MUT,即MTBCF):
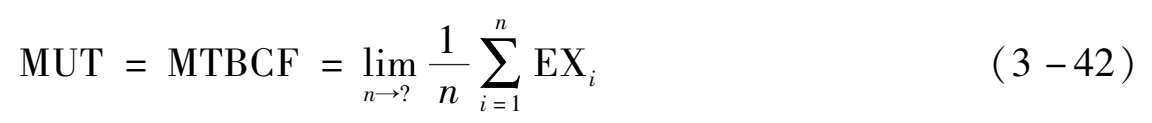
定时检修系统与在线维修系统在结构组成上是类似的,主要针对表决冗余或并联冗余系统。二者的区别在于在线维修系统可在不关机的情形下直接维修更换单元、组件;定时检修系统由于受到风险因素制约,需要产品关机或关发射后再进行检查和故障单元更换工作。这种定检工作可结合预防性维修时机同步进行,既保证系统的任务可靠度,又减少系统停机时间。
图3-25考虑维修特性表决冗余系统
运用马尔科夫过程方法对在线维修系统进行可靠性建模评估。考虑如图3-25所示的 k / n 表决系统的在线修理模型。
假定系统由 n 个服从指数分布的相同设备组成。有一个修理设备,故障后的修理时间为1-e- μt , μ 0,故障部件均能准确定位并修复,修复后其寿命分布和新部件一样。由于只有一个修理设备,当它正在修理一个故障部件时,其他故障部件必须等待修理。
根据 k / n 表决系统的基本定义,有:
1) k 个或 k 个以上部件正常工作时,系统正常工作(1≤ k ≤ n );
2)当有 n - k + 1个部件故障时,系统故障。在系统故障期内, k -1个正常部件停止工作,不再发生故障。直到正在修理的部件修理完成, k 个正常的部件同时进入工作状态,此时系统重新进入工作状态。
定义 X ( t )= j,j =0,1,…, n - k + 1,表示时刻 t 系统有 j 个故障的部件(包括正在修理的部件)。可知{ X ( t ), t ≥0}是状态空间 E 的齐次马尔科夫过程,Δ t 内的状态转移概率为:

绘制的系统状态转移概率图如图3-26所示。
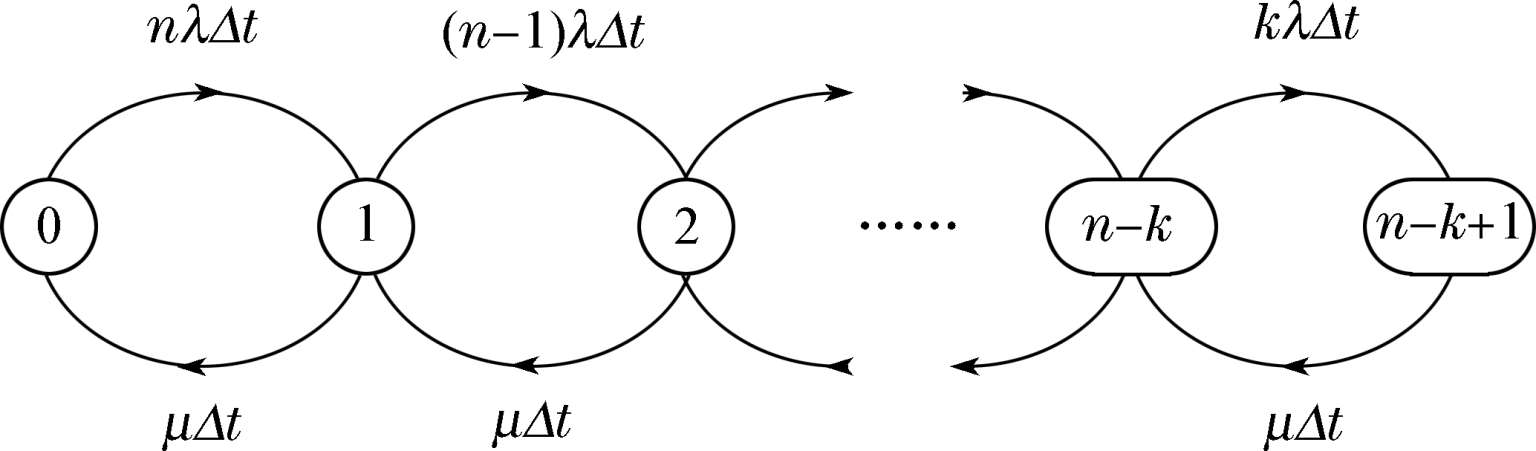
图3-26 k/n(G)表决系统单维修设备在线修理状态转移概率图
状态转移速率矩阵为
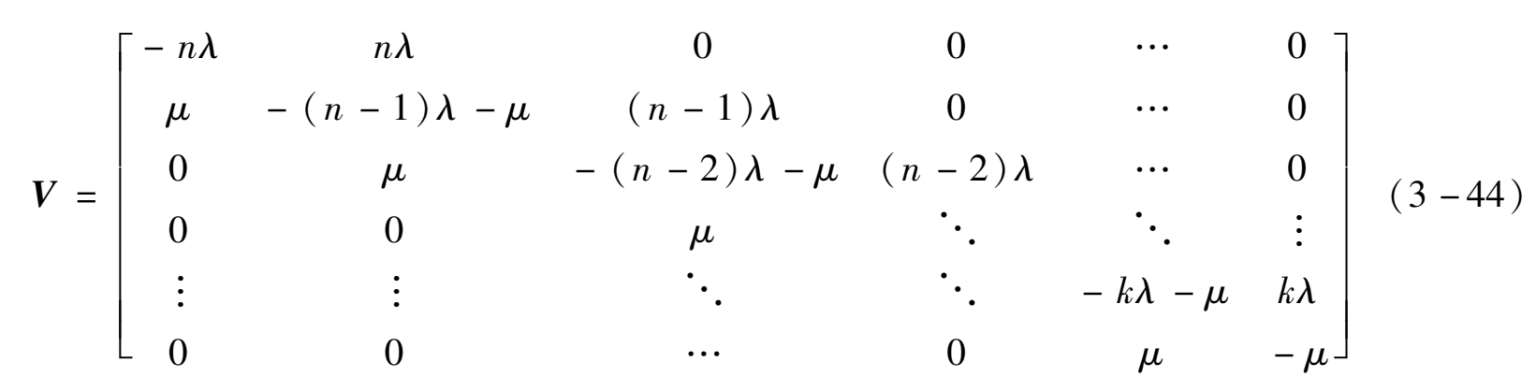
令 P ( t )=[ P 0 ( t ) P 1 ( t )… P n-k + 1 ( t )];
初始条件 P 0(0)=1, P 2 (0)= P 2 (0)=…= P n-k + 1 (0)=0;
建立微分方程
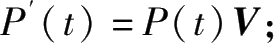
这是一个微分方程组,可在方程组两端作拉普拉斯变换再求解。根据求解结果可计算得到系统的可用度
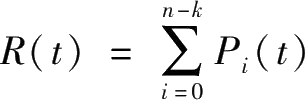 。
。
系统的瞬时指标比较难以求得,但平均指标和稳态指标可以求得。稳态可用度:
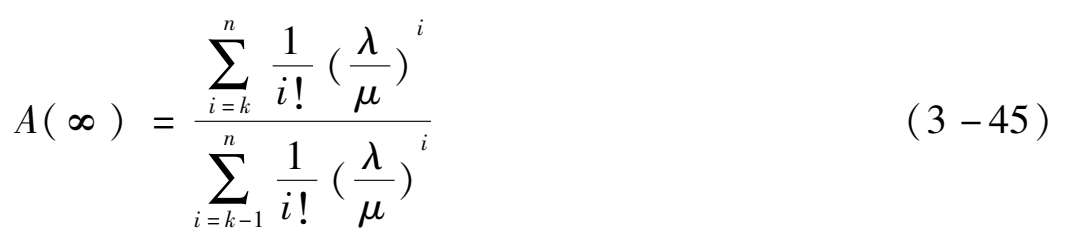
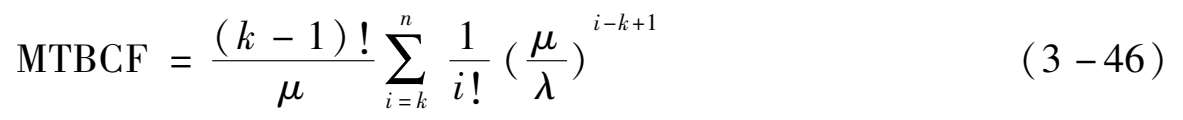
此外,对 k = n -1情形:

通过建立马尔科夫模型可以清晰地表示出系统状态之间的转换关系,同时由转换概率可求得系统的可靠性指标,能够充分表征系统带故障运行能力,有利于对系统的可靠性进行准确全面地评估。
[例3-3] 信息处理设备采用了8取6表决设计,且可在线维修,求解MTBCF。
采用连续时间马尔科夫链描述。定义工作状态和故障状态,记转移速率矩阵为 V 1 。
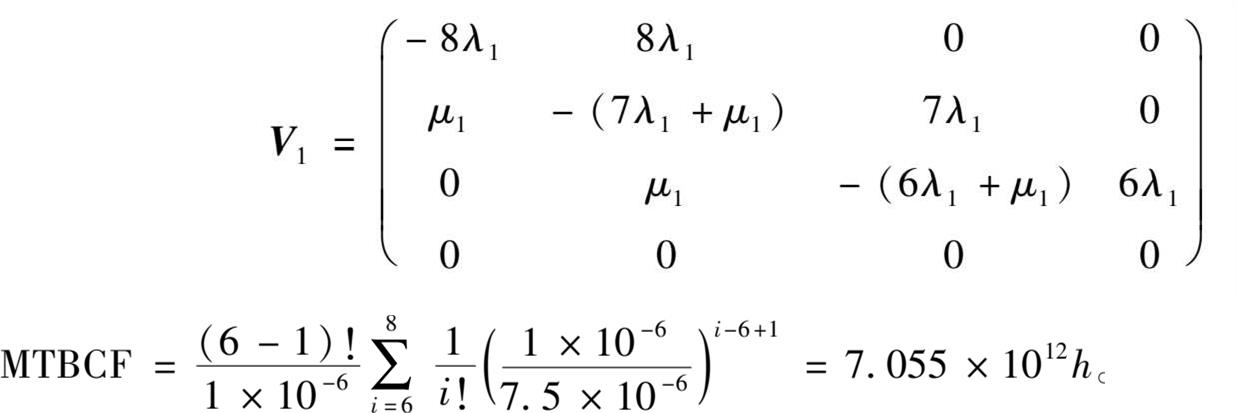
采用在线维修后显著提升了信息处理系统的任务可靠性。
并联在线修理时, MTBCF=(3λ + μ )/2λ 2 。
如图(3-24),假定单元可靠度为 r ( t ),在第一个周期中单元可靠性为:

将 r ( t )代入 k / n 冗余系统公式中,可得到:
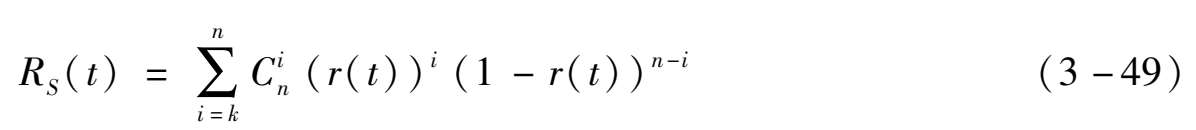
式中: n —单元总数; k —系统正常工作所需的无故障单元数;λ—单元失效率。
由于引入了定期维修,系统可靠性
R
S
(
t
)已经是一个多阶段的函数,无法使用MTBCF =
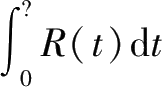 去计算系统的MTBCF,因为所得到的值是无穷大。在完美维修情形下,单元可靠性呈现周期性变化,对应的系统可靠度也呈现周期变化,有:
去计算系统的MTBCF,因为所得到的值是无穷大。在完美维修情形下,单元可靠性呈现周期性变化,对应的系统可靠度也呈现周期变化,有:
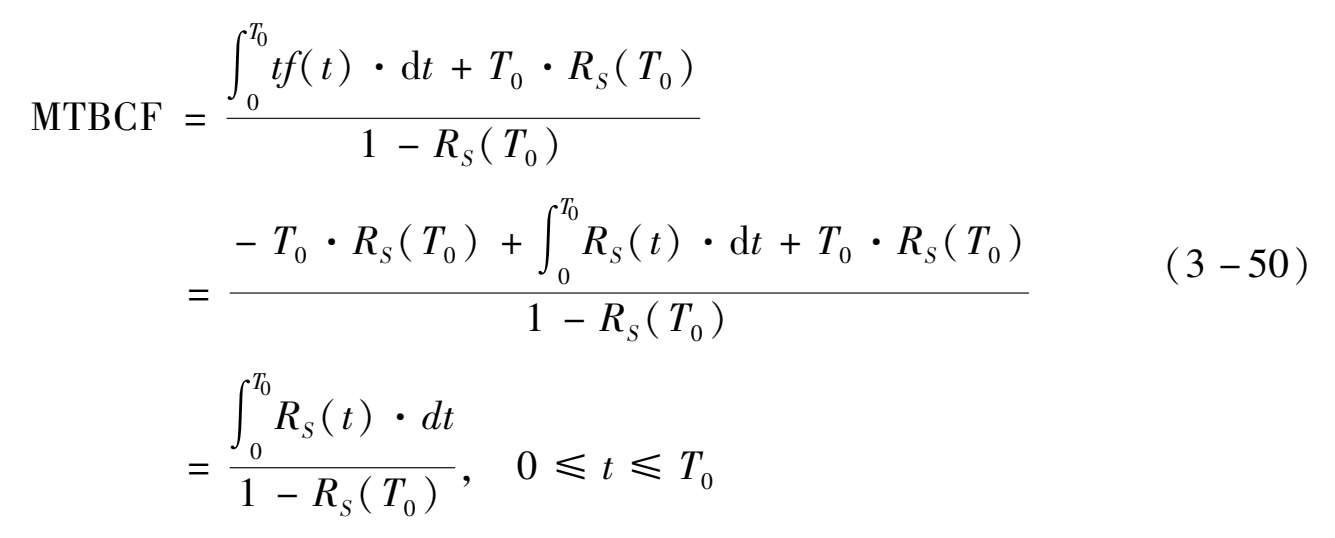
式中: T 0 为检修周期。
联立可得:
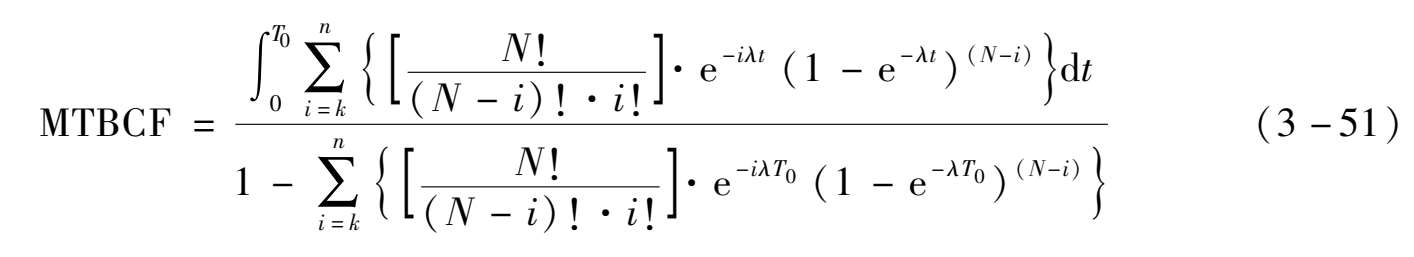
考虑到公式的积分计算存在一定难度,同时对于定时检修系统,在一个检修周期结束时系统可靠度应维持在一个较高水平(如0.99以上),因此上述MTBCF计算可采用近似公式:
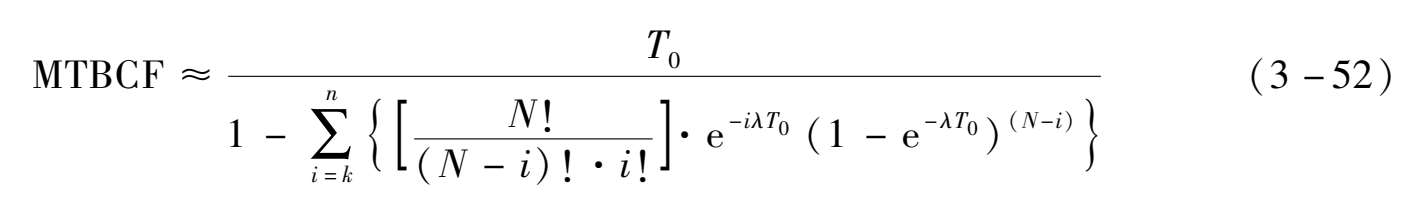
检修周期结束系统可靠度大于0.99时,该近似公式提供的MTBCF是比较准确的,误差不超过半个周期的长度。
考虑故障检测率、故障隔离率等检测参数和故障修复率时,不完美检测维修下的定期检修系统可靠度:
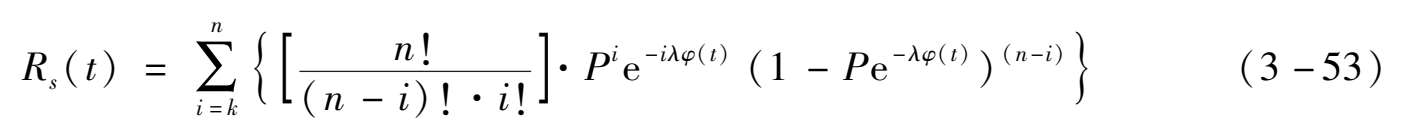
式中:φ( t )= t -INT( t / T 0 )· T 0 ;INT()—向下取最接近的整数; T 0 —定期检修周期。
P为检修周期开始时单元的完好概率:
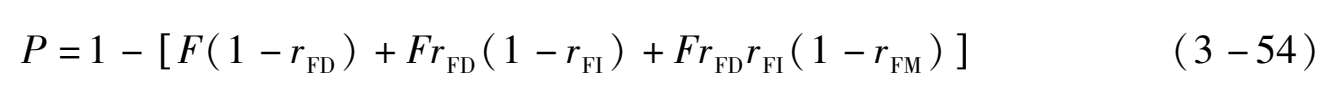
式中: r FD —故障检测率; r FI —故障隔离率; r FM —故障修复率。
F 为一个检修周期内单元的故障概率:

此式中各个维修周期下系统任务可靠度是周期性变化的,仍可依据(3-50)的方法计算:
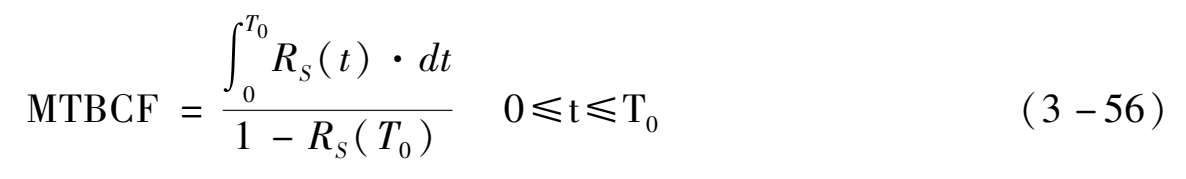
假定在第 i 个检修周期初始时刻单元完好概率为 r i ,故障概率为 f i ,有 r i + f i =1。
在一个完整的检修周期(工作+修复)中,经分析有:
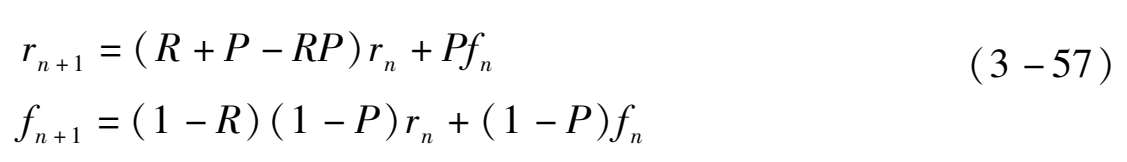
式中:
R =e- λT0 ,为一个检修周期中单元不发生故障的概率;
P = r FD r FI r FM ,为发生故障的单元进行维修时修复完好的概率。
由于 r 1 =1, f 1 =0,推导可得:
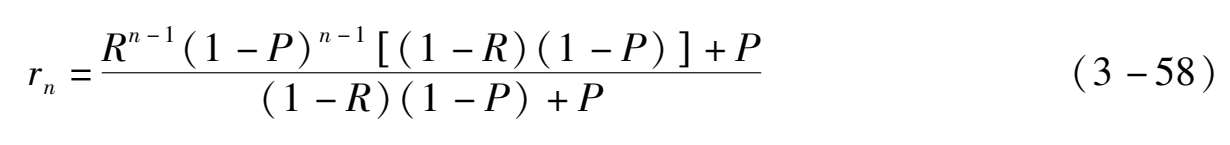
因此,在第 j 个检修周期系统可靠度为:
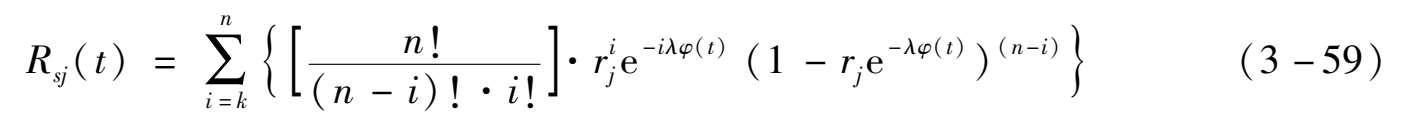
随着检修周期的进行,有:
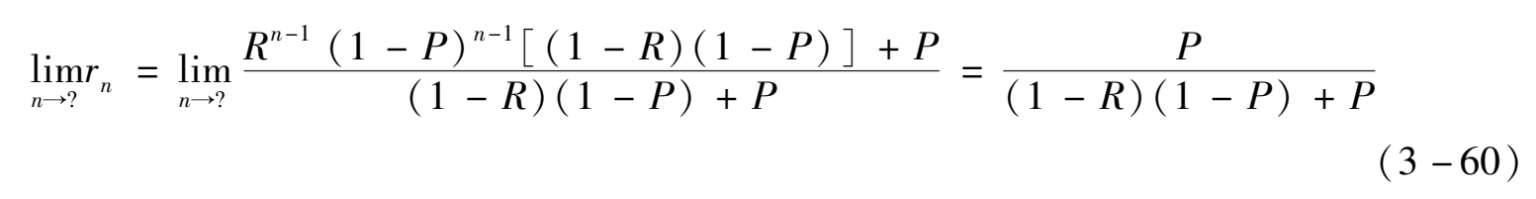
假定在多个检修周期之后,系统可靠度呈现周期性变化,有:
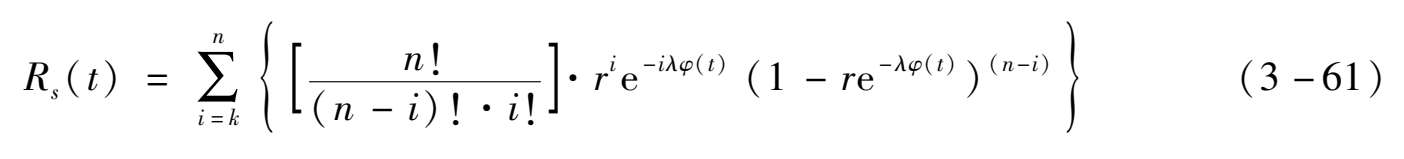
式中:
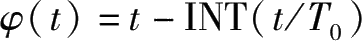
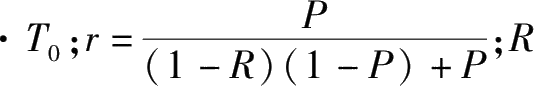
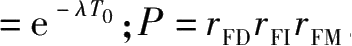 。
。
此时有:
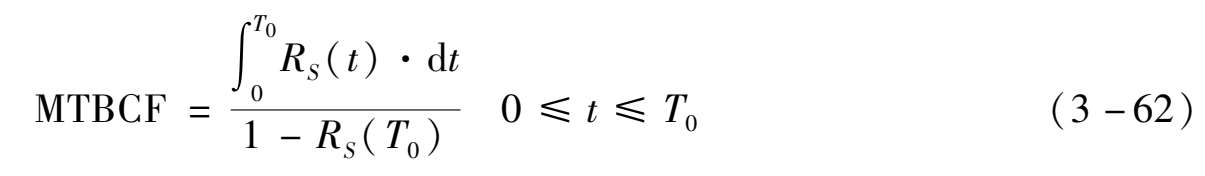
进一步观察发现,解析算法2中 P 即为解析算法1中 r 。因此,解析算法1是一个近似公式,认为从第二个周期开始,系统可靠度可看成是周期性变化的;而经过解析算法2推导发现,在不完美维修情形下系统可靠度并不呈现周期性变化,解析算法2给出的是在极限情况下系统MTBCF。
在不考虑维修时间的情况下,冗余系统的可靠度可以表示为:
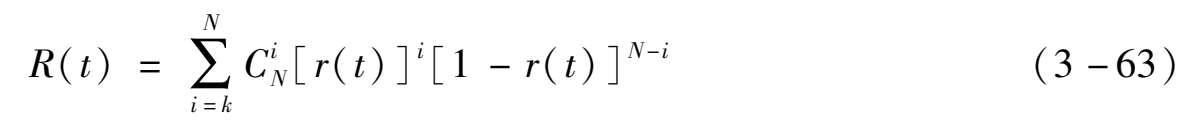
其中 r ( t )=e- λ0t ,为不考虑维修时间下的单组件可靠度。
对于单位组件的定期检修,如果需要用精确算法,则需要按照每一期检修的结果和维修后是否修复进行逐步分析,最终形成归纳计算。如图3-27所示。
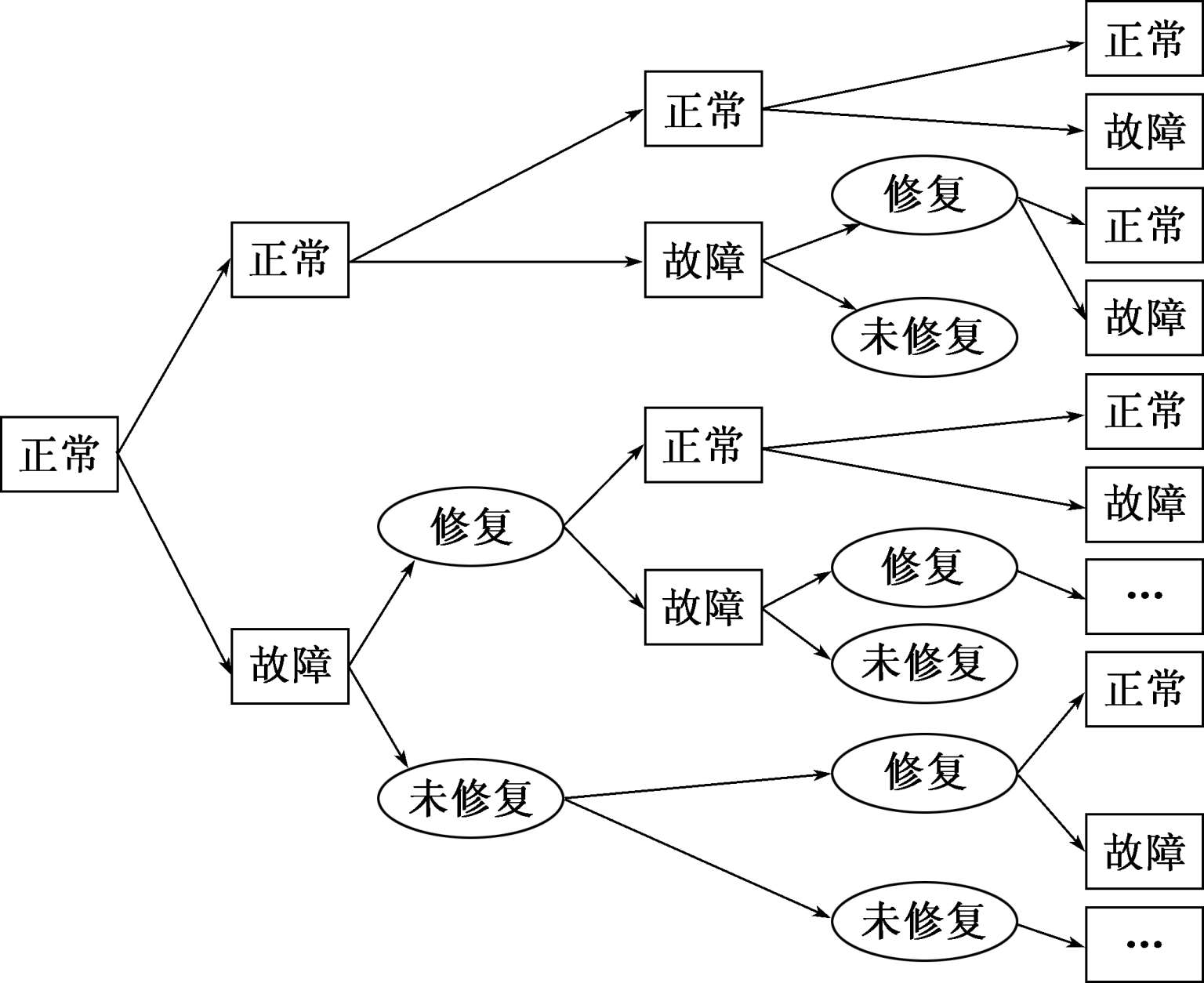
图3-27定期检修逐步归纳
例如,在第一个周期中,单元可靠性和基本可靠性一致,即: r ( t )=e- λt 。
在一个维修阶段后,即第二个运行周期内(T-2T),单元的可靠性可以表示为:
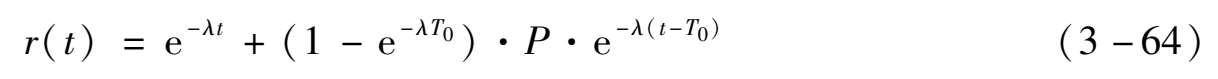
第三个运行周期内(2T-3T),需要计算总共五种可能的情况,最后得到单元的可靠性可以表示为:
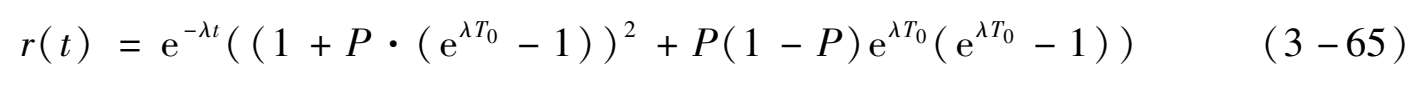
第四个运行周期内(3T-4T),可以得到单元的可靠性:
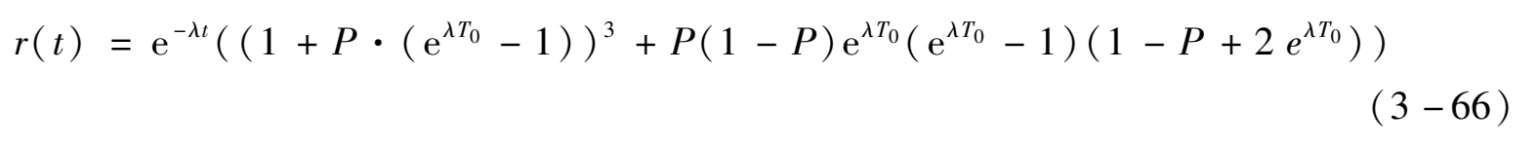
接下来的多个运行周期都可以用该方法进行推倒,得出所需时间的单位可靠度。最后可以将 r ( t )带入到 k / n 冗余系统的公式中,可以计算最终的系统可靠性。
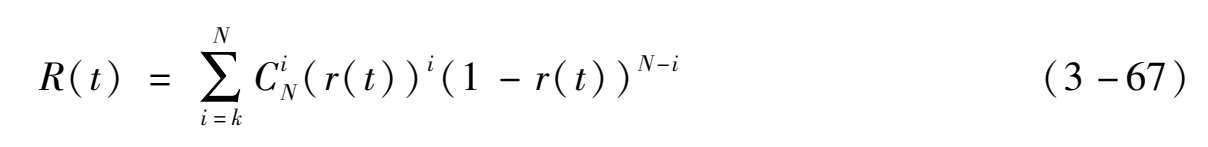
在计算MTBCF时,情况较为复杂,根据一般公式
MTBCF
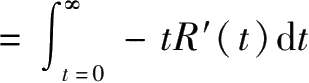 。
。
假设第
n
个周期维修结束后,组件正常工作的概率为
R
n
(
T
),不能正常工作的概率为
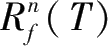 。
。
其中:
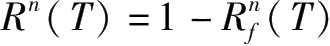 。
。
现在归纳 n -1周期维修后过度到 n 周期维修后的情况。首先 n -1周期维修结束后有正常和不正常两种工作状态,正常状态下在经历n周期后可能出现正常和不正常两种状态,再根据不同状态进行维修,维修又有一定概率成功和失败;而不正常状态下, n 周期不能工作,只能在结束后继续维修,并以 p 的概率成功维修。
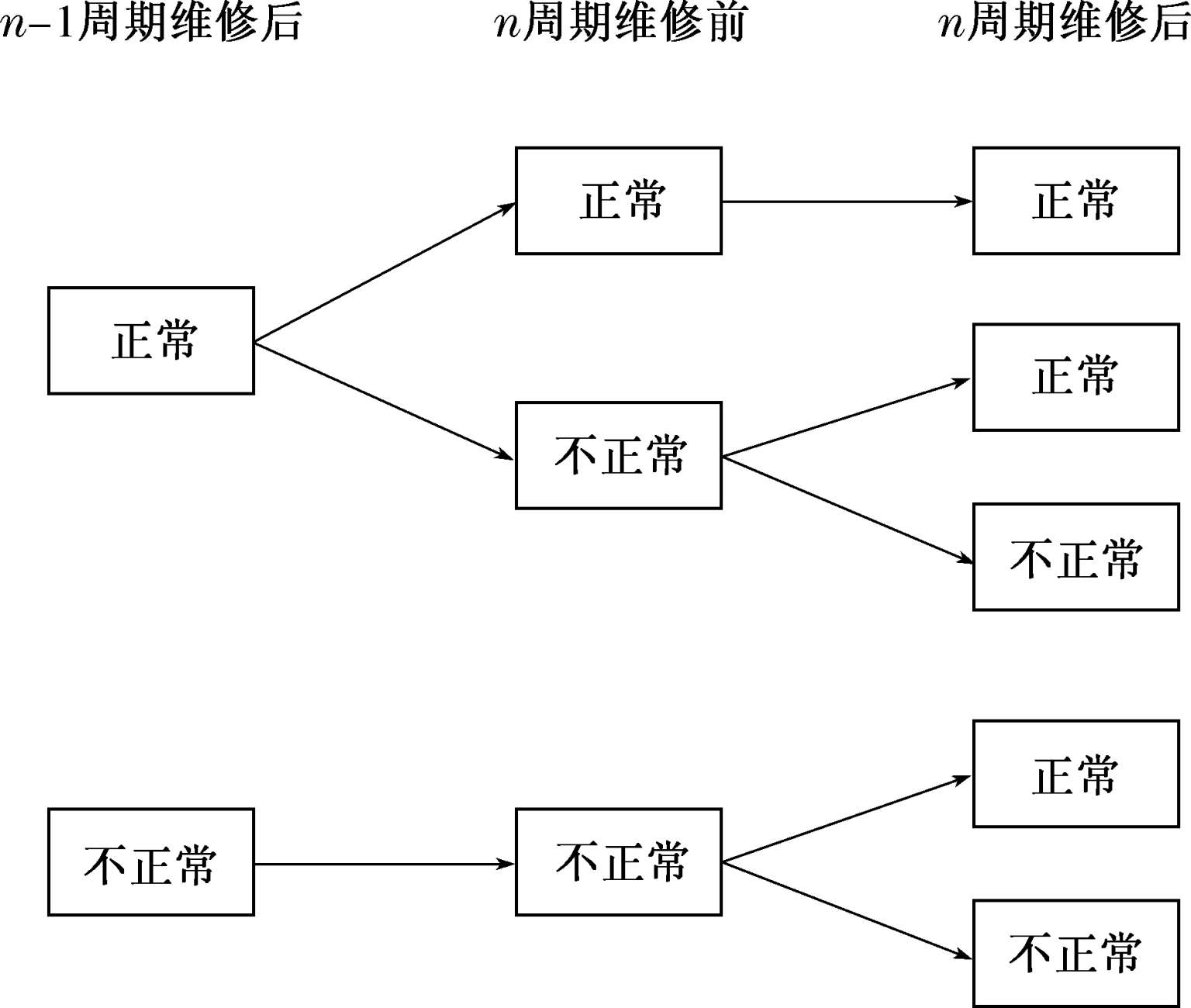
图3-28第n周期系统状态
因此,可以得到第 n 个周期维修后的 R n ( T )可以写为:
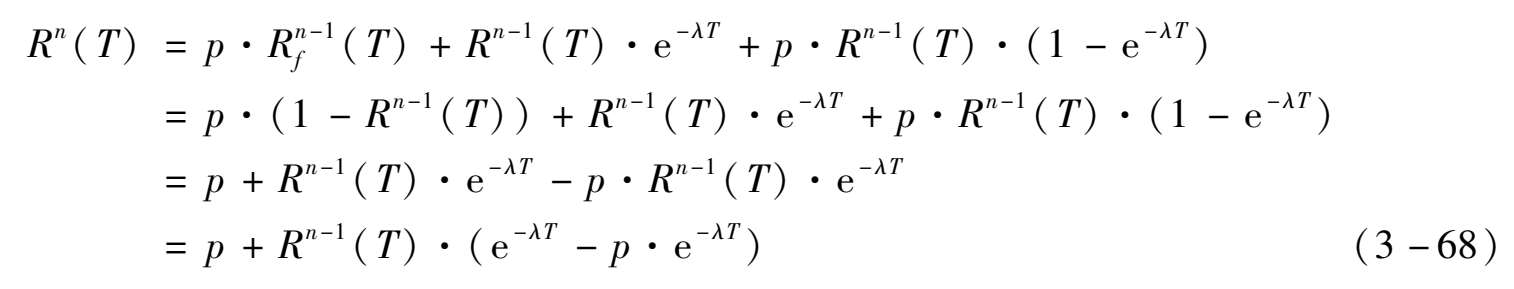
变换为等比数列:
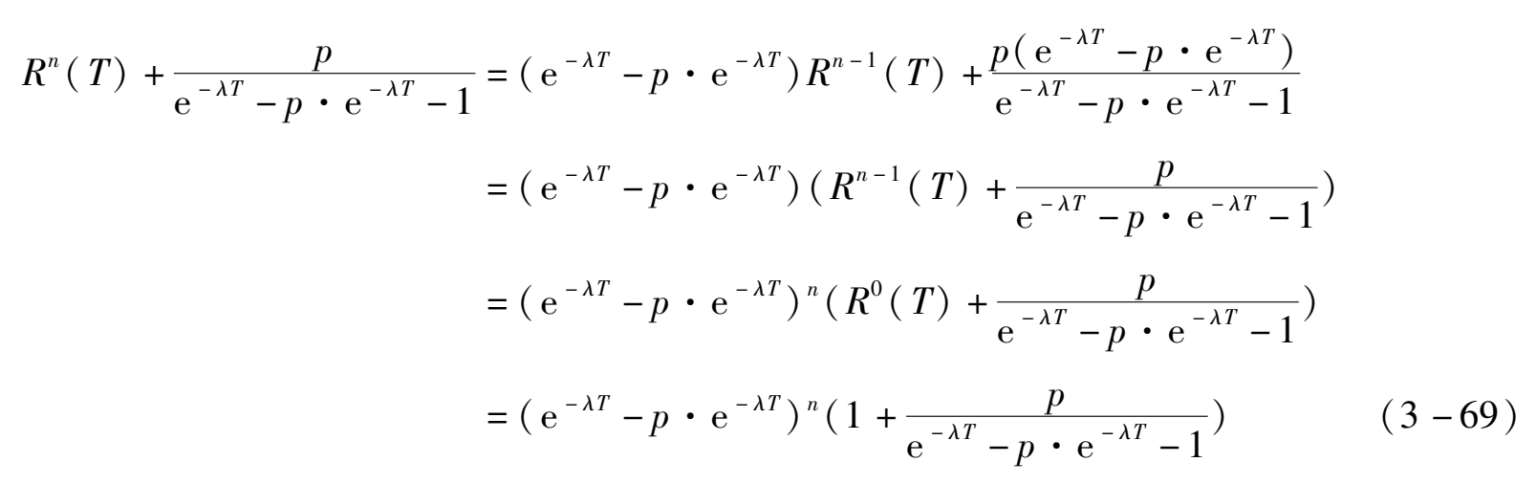
因此:
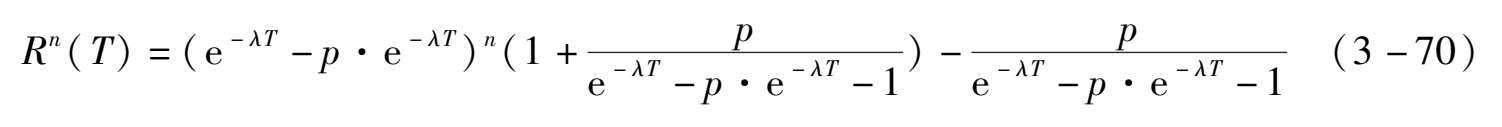
在第 n + 1个周期内的工作概率则可以表示为: r ( t )= R n ( T )e -λ( t- n T ) 。
由此可以通过递归方法得到需要查找的周期内的可靠性。
例如:如图3-29的四合一模块,假设需要四个模块,有两个以上可以正常即可正常工作。
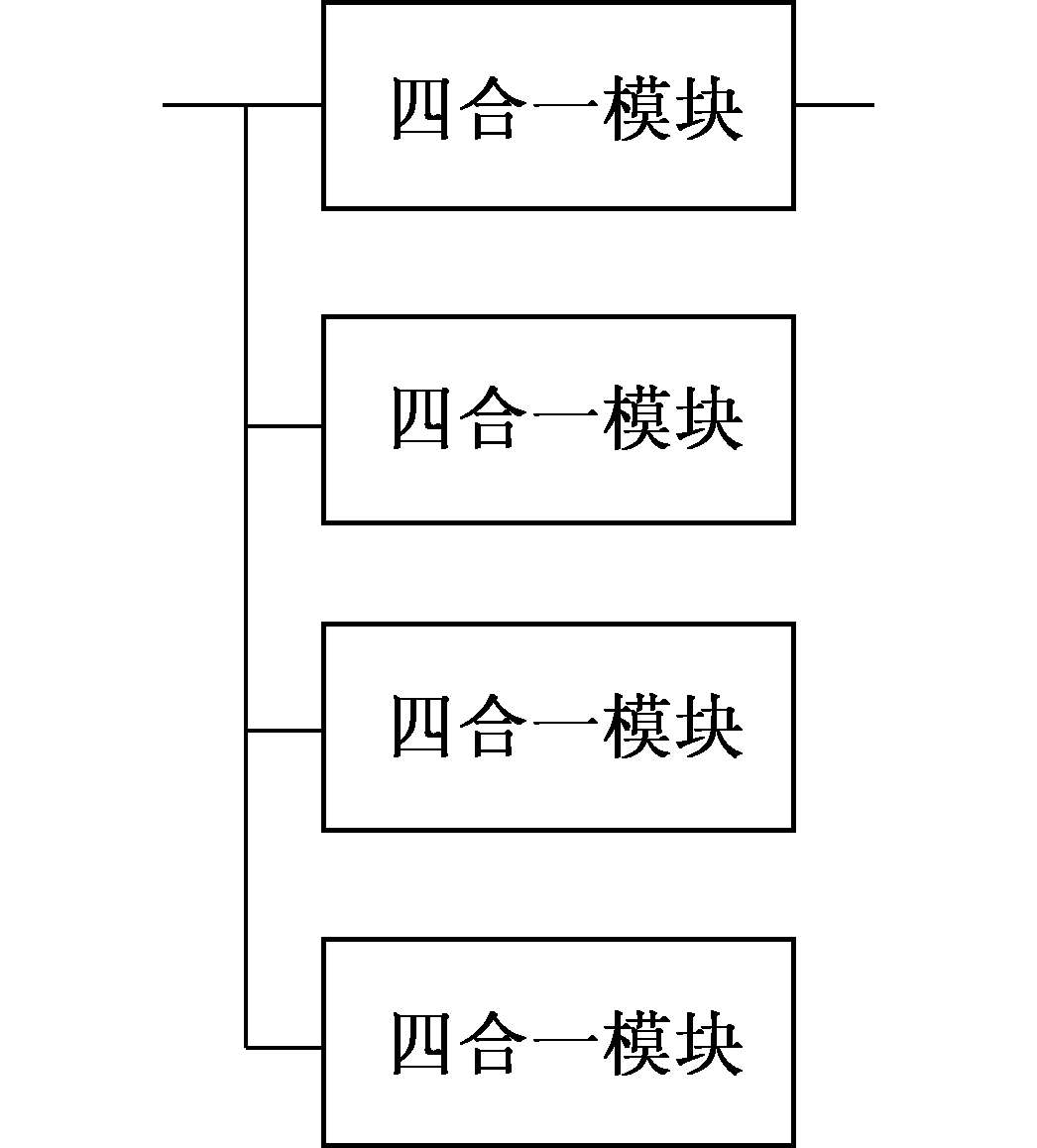
图3-29四合一模块
探求第 n 个周期内,即( n -1) T t nT 的可靠性:
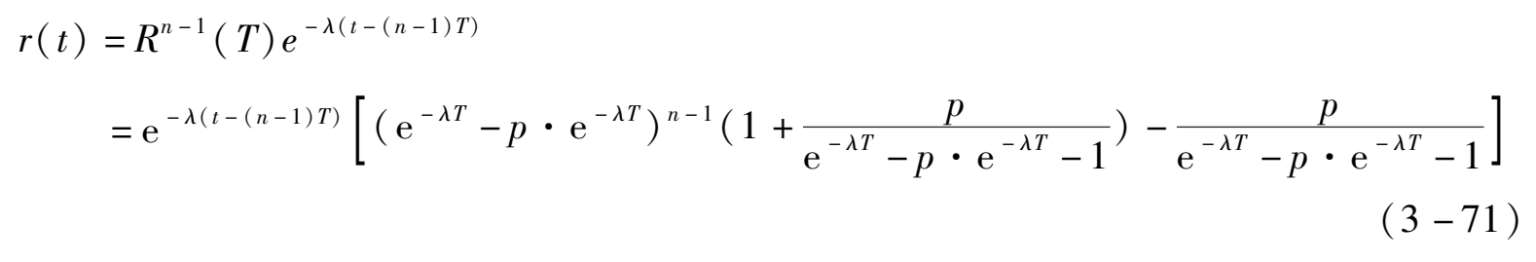
在第 n 个周期时间区间段内2 /4模块系统整体可靠性可以表示为:
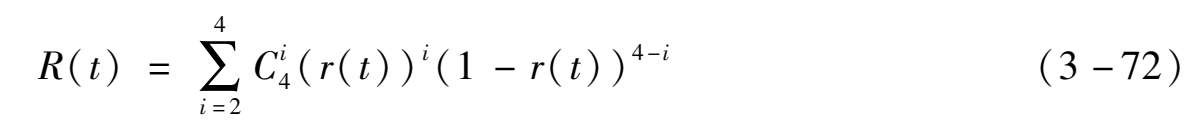
讨论的系统模型,运用到实际系统可靠性评估中,还需要确定下几个较强的假设,包括维修时间、维修周期结束即使无法运行也需要等待下一个周期维修,以及系统维修率等问题设定。在确定了问题条件后,可以通过优化多个阶段可靠性计算方法和递归算法实现求解(若级数较高求优化求解近似解),并可以与仿真方法进行比较。
对于 n 取 k 表决冗余系统,计算步骤如下:
a)输入定期检修系统相关参数,包括单元总数 n ,系统正常工作所需的无故障单元数 k ,单元失效率λ,检修周期 T R ,设定的步长 t ,仿真次数 M ,检测率 P 1 ,隔离率 P 2 ,修复率 P 3 等;
b)开始进行第一次仿真,仿真步骤如下:
1)初始时刻,根据失效率对每个单元随机生成对应的故障时间序列,记录此时刻的故障位置记录序列和故障数;
2)当前时刻+ t ,根据生成的故障时间序列判断此时刻单元是否发生故障,更新此时刻的故障位置记录序列和故障数;
3)若此时刻故障数大于 n - k ,系统无法正常工作,记录此时刻故障时间 TF 1 ;否则重复2);
4)当时刻到达检修周期,更新此时刻的故障位置记录序列和故障数,若此时刻故障数大于 n - k ,系统无法正常工作,记录此时刻故障时间 TF ;否则根据故障位置记录序列,针对发生故障的单元按失效率重新生成对应的故障时间序列(或按检测率 P 1 ,隔离率 P 2 ,修复率 P 3 部分更新);
5)重复2)~ 4),直至达到设定的程序仿真时间截止限,得到故障时间序列{ TF 1 };
c)按设定的仿真次数继续进行仿真得到每次仿真的故障时间序列;
d)假定第 i 次仿真中得到的故障时间个数为 L i ,则该定期检修系统蒙特卡洛仿真得到MTBCF为:

仿真参数中仿真次数、仿真步长和仿真截止限对仿真结果的精度有直接影响,仿真次数越多、仿真步长越小,仿真结果精度越高,而蒙特卡洛仿真花费时间也越长。
[例3-4] 取 n =50, k =45,λ=50× 10 -6 /h, T 0 =720h, r FD =0.9, r FI =0.9, r FM =0.9。
蒙特卡洛仿真步长10h,仿真次数10000次。
得到三种算法下可靠度变化趋势如图3-30所示:
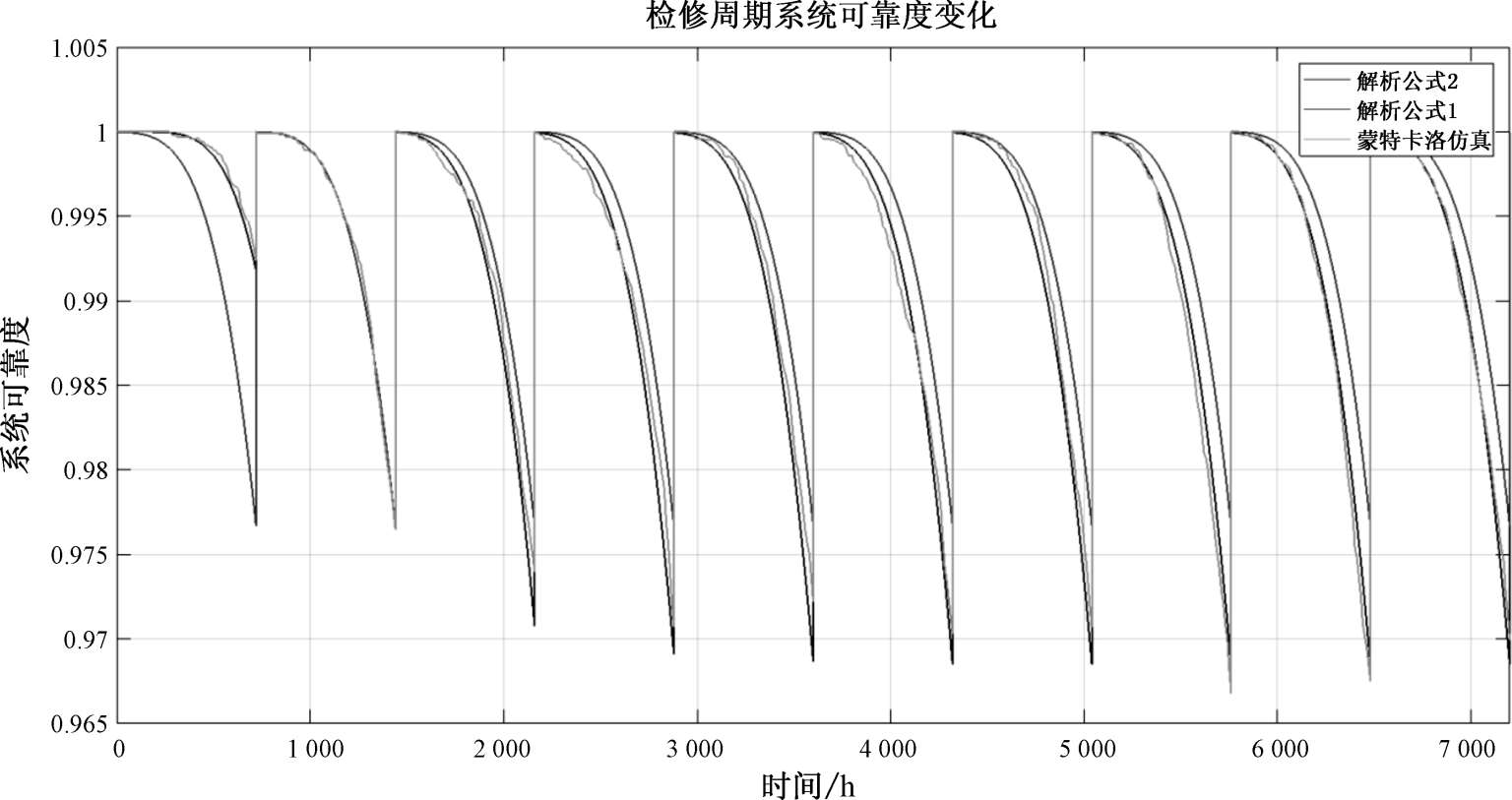
图3-30检修周期系统三种算法可靠度比较
通过上图可以看出,蒙特卡洛仿真结果与解析算法2计算结果有较好的吻合,尤其是在较后的检修周期中。解析法和蒙特卡洛仿真法原理不同,在完美维修情形和不完美维修情形下,解析算法2和蒙特卡洛仿真结果相对误差均小于5%;考虑到案例中仿真次数较少,因此可认为蒙特卡洛仿真结果和解析算法2的计算结果是一致的。由于解析算法2是解析公式,计算所需时间小于蒙特卡洛仿真时间,因此在工程上可使用解析算法2进行定时检修系统MTBCF计算,也可使用递归算法1或2。