




Petri网(PN-Petri Net)是一种被广泛应用于系统描述和分析的数学工具。 Petri网是一种图形化的建模和分析工具,近来被广泛地应用于离散时间动态系统等领域,是进行系统性能评价的重要工具。
Petri网是一种二元有向图,它是节点集与弧集的集合,用圆圈表示的节点被称为位置,用直线或矩形表示的节点被称为转换,一般用直线表示的转换为无延时的转换;而用矩形表示的转换为有延时的转换。带有空心小圆的弧被称为限制弧,实心圆点被称为令牌,系统的动态过程可通过令牌在图中的移动来直观地表示。而令牌的移动是由Petri网中转换节点的引发规则实现的,当指向转换节点的常规弧所在的位置节点有令牌而限制弧所在的位置节点无令牌时,转换被引发,同时令牌被传送到新的位置。通过引发规则,可以遍历系统所有的可达状态。如果再令图中所有的延时转换中的时间分布为指数分布,则系统的状态变化过程可用马尔可夫过程描述,这就是一般随机Petri网即Generalized Stochastic Petri Nets(GSPN)。
Petri网,特别是随机Petri网在系统可靠性分析中占有重要位置,其研究的基本方法在相关的理论研究和案例分析中主要可以分为5大类:系统的基本行为描述方法、系统的故障树简化方法、系统的故障诊断研究方法、系统可靠性指标的解析计算方法和系统可靠性仿真分析方法。
a)系统的基本行为描述方法:根据已经建立的系统Petri网模型,分析模型系统的可达性、可逆性、活性等动态性质,从这些性质分析中总结系统具备的一些行为特点,为可靠性分析和研究做好铺垫工作。
b)系统的故障树的表示与简化方法:故障树分析模型是一种传统的可靠性分析方法,可以将故障树看作系统中的故障传播的逻辑关系,将故障树转换成Petri网模型,通过可逆网的可达性或者通过关联矩阵的计算,得到最小的割集。
c)系统的故障诊断研究方法:基本网系统是Petri网系统的一个特例,在基本网系统中,一个库所最多含有一个标识,可以利用库所的这种标识特性,通过可达标识来判断相应的故障是否发生。
d)系统可靠性指标的解析计算方法:可靠性指标也是系统性能指标的一个重要组成部分,通过一般数学分析方法对可靠性模型进行分析,一般仅能给出某些参量的计算方法。由于一般的数学分析方法不具备反映中间过程的能力,而基于Petri网模型的可靠性指标计算方法,在和数学方法满足相同的约束条件下,可以清晰地描述系统状态之间的动态转移过程,这种特点以随机Petri网(Stochastic Petri Nets,简称SPN)最为明显。
e)系统可靠性仿真分析方法:随着计算机工程的应用技术的发展,可靠性的分析与研究不仅仅局限在可靠性指标的计算、故障诊断等方面,还体现在复杂系统的可靠性仿真分析研究上。仿真分析是计算机研究和可视化分析的重要途径,因此可以利用已有的仿真分析工具对可靠性进行建模、分析和模拟,为可靠性研究在工业应用中拓宽应用广度。
对可靠性研究比较成熟的方法是利用随机Petri网对可靠性进行建模,然后将可靠性或可用性的求解指标计算转换为同构的马尔科夫链的计算。通过Petri网构建的SPN模型,建立网系统的关联矩阵(即状态转移概率矩阵),通过计算机求解或者解析求解可靠性或可靠性的性能指标。
定义1:Petri网是一种有向图,由变迁、库所、令牌和有向弧四个部分组成。
定义2:若PN是一个四元组,且 PN =( P , T , A , M )并满足以下条件:
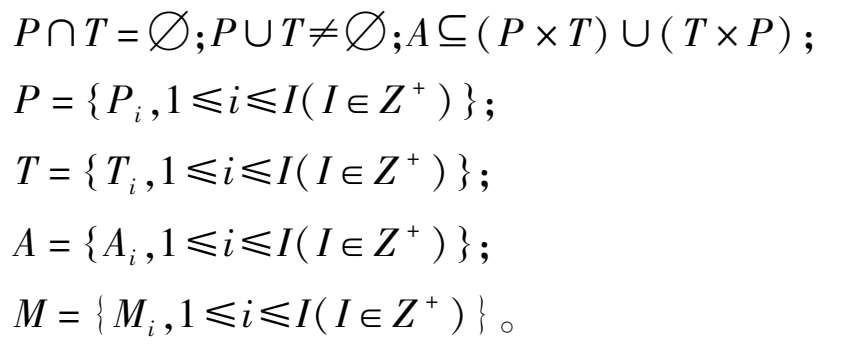
其中 P i 是库所; T i 是变迁; A i 是从变迁到库所或从库所到变迁的一个有向弧; M i 是令牌数目的集合,令牌是一种条件或状态是否成立的状态,这些令牌包含系统在不同状态下所有库所的令牌,则称PN为Petri网。
定义3:变迁在Petri中使能的条件是,该变迁的任意一个输入库所包含的令牌不少于一个。
定义4:若变迁满足定义3,并把此变迁的所有输入库所中的一个令牌移到库所的所有输出库所中去,称该变迁被激发。
由上述定义可以看出Petri网是用来描述系统处于静态时的性质,并没有引入时间概念。下面给出随机Petri网的定义为:
定义5:随机Petri网由七元组构成,SPN=( P , T , F ; K , W , M 0 ,λ)。 P , T , F , K , W 的定义和加权Petri网定义相同;λ={λ 1 ,λ 2 ,…,λ m }为变迁激发速率集合。
在可靠性建模中,1 /λ i 表示变迁 T i 的平均延迟时间。
在随机Petri网中,变迁是用来描述系统所处的状态事件。库所是用来描述系统可能处于的局部状态,如系统中元器件所处的运行、失效或者维修状态。令牌是库所的一部分,令牌的动态变化能够表示系统及元器件所处的状态。弧是用来描述事件及局部状态间的关系,有两种描述方式:一种是引述事件发生的局部状态;另一种是利用事件引发局部状态转换。由上述定义与、或、禁止、补、与非、或非等逻辑关系均能用Petri网表示。(如图3-17所示)
已经证明,若SPN为K(某一常数)有界,则SPN模型与连续时间马尔科夫(CTMC)状态一一对应,且可以通过线性方程组求得系统概率分布,从而得到系统的可靠性特征量。 SPN的优点是可以通过计算机自动进行马尔可夫过程的状态分析,并通过状态方程得到系统的可靠性指标。
令 p i ( i =0,1,2,…, n )和 q j ( j =0,1,2,…, n -1)分别表示系统处于正常状态的位置和故障状态的位置的稳态概率。利用下式可以求出该系统处于各位置的稳态概率:
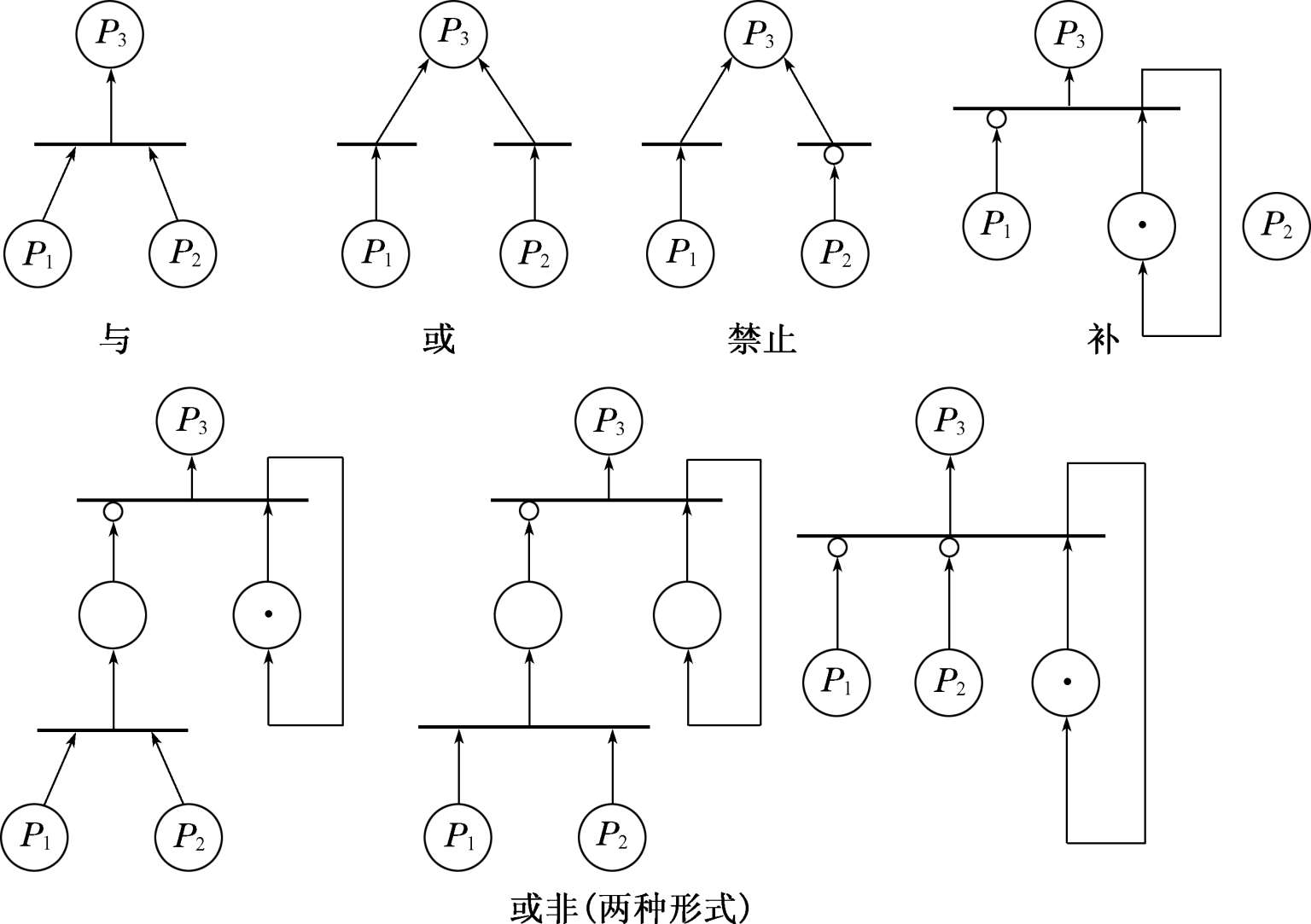
图3-17 Petri网的逻辑关系模型

式中, P i 表示稳态情况下处于位置 p i 的概率, Q j 表示稳态情况下处于位置 q j 的概率,Π是元素为 P i 、 Q j 的稳态概率矢量, K 为变迁状态转移矩阵。
应用SPN的分析方法有解析法和仿真法,解析法将SPN的可达图映射成MCs的状态转移矩阵,然后用经典的MCs方法进行分析。但是随着系统的复杂性、关联性的增强,与SPN同构的MCs难以获得,系统状态空间的组合爆炸是最突出的问题,而且MCs方法要求Petri网变迁的时延服从负指数分布,否则难以求解。 Petri网动态仿真可在一定程度上避免定量分析中的维数灾难问题,但是通过动态仿真只能得到可靠性指标的数值解,而无法求解相关指标的解析解。
图3-18为串联系统的随机Petri网模型。其中,元器件出现故障用dn表示,元器件正常工作或者等待工作时用up表示。一个串联系统由n个独立元件组成。
利用串联系统的随机Petri网模型对系统进行动态分析如下:串联系统的所有单元的up库所在系统开始运行时均含有令牌,变迁 t 1 、 t 5 、 t 7 、 t 8 处于使能状态,其中变迁t 1 处于瞬时变迁状态,不存在实施延时,能够立即被激发,与此同时将串联系统所有单元的输入库所up中的一个令牌移入所有单元的输出库所dn中去,再向Sys. up中移入一个令牌。此时 t 1 中的令牌与Sys. up中的令牌相等, t 1 被禁止。随着系统的运行某个单元会失效,假设系统运行一段时间后,单元1失效,则单元1的输入库所up中的一个令牌移入输出库所dn中去,变迁 t 2 、 t 6 处于使能态, t 5 被激发。 t 2 为瞬时变迁,不存在实施延时,能够立即被激发,激发后Sys. dn出现令牌,此时 t 9 满足被激发的条件,即移走Sys. up和Sys. dn中的令牌。由于Sys. up和Sys. dn中的令牌被移走, t 2 再一次被激发,Sys. dn又被移入令牌。这时变迁 t 2 、 t 3 、 t 4 、 t 5 、 t 7 中的令牌数目与禁止弧上所标注的数目相等,则上述变迁均被禁止。对系统进行维修后单元1恢复正常工作,则 t 6 被激发,令牌在单元1中的输入up库所中出现。则 t 1 被激发,Sys. dn库所中的令牌移入到Sys. up库所中,系统恢复正常运行状态。若串联系统中随机Petri网模型的全部延时变迁的延时时间服从指数分布,则随机Petri网模型与马尔科夫模型同构。
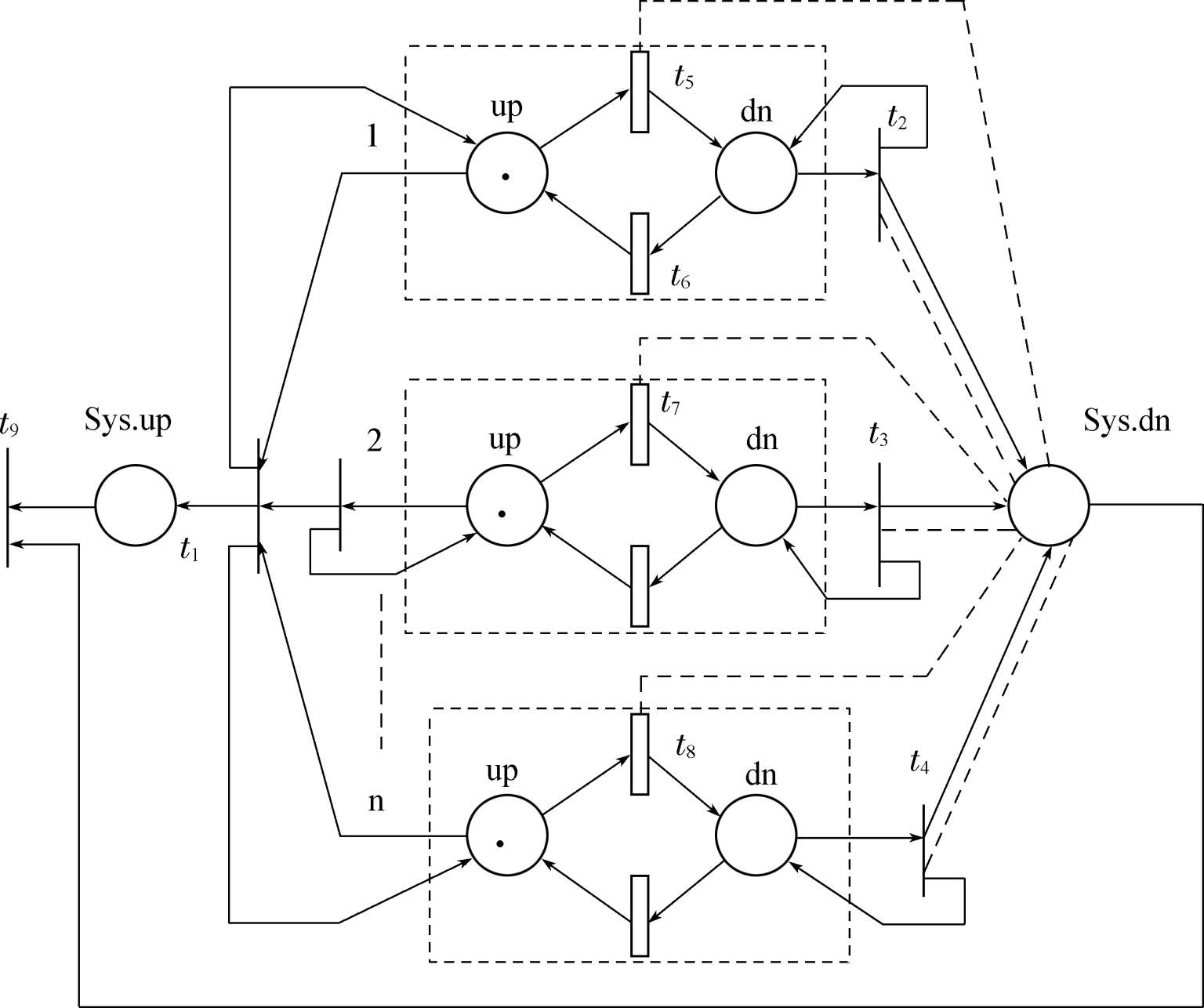
图3-18串联系统的随机Petri网模型
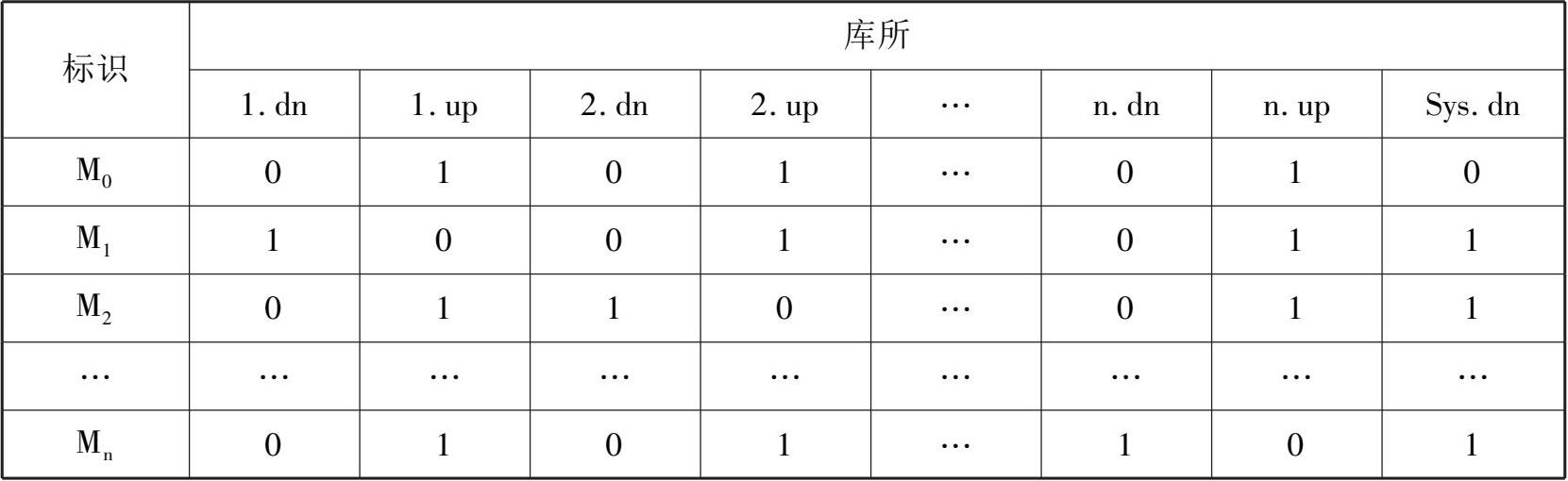
表3-6为串联系统SPN模型的状态标识库所。
表3-6串联系统SPN模型的状态标识库所
除了经常使用的随机Petri网,还有许多其他形式的Petri网系统被应用到可靠性的建模与分析研究中,如有色Petri网、面向对象Petri网、时序Petri网、时间Petri网、受控混合随机Petri网等等。值得一提的是,应用时间Petri网研究可靠性其实是嵌入到基于随机Petri网或者有色Petri网的可靠性研究中的一种特例,在系统分析中基于时间Petri网的建模与仿真仅仅专注于系统行为在时间维度上的特点,因此时间Petri网可以作为有色Petri网或随机Petri网的一个子类来进行考虑。
面向对象Petri网(Object-Oriented Petri Nets,简称OOPN),是将面向对象编程的思想融合到Petri网建模过程中,突出各个对象或类之间的交互情况。基于OOPN的建模方式有利于软件开发人员根据所建立的OOPN模型实施软件系统的设计工作,在许多实际的应用系统中有较广泛的应用。
时序Petri网(Temporal Petri Nets,简称TPN)。由于Petri网和时序逻辑被认为是分析并发系统重要且有效的两种理论工具,TPN将Petri网和时序逻辑结合在一起,同有色Petri网、随机Petri网等一般Petri网类型相比,它能够较好地表达事件间的时序关系以及并发系统中与时序相关的性质。
受控混合随机Petri网。除了一般Petri网考虑影响系统行为的离散变量,混合随机Petri网还考虑了连续变量,将离散变量和连续变量作为影响系统行为的两种因素,比较客观和完整地表示系统特点。这类系统在建模语义的表示上更加准确和详细,但是难点就是分析工具比较欠缺,除了可达标识图,还未见其他较完善的分析技术。
在系统的建模分析中,除了随机Petri网以及其他类型的Petri网变型系统,还往往将计算机科学中一些比较先进的技术和算法融合进来,在可靠性研究领域形成一个重要的研究领域。
与随机Petri网技术联合使用的分析方法,主要有蒙特卡洛方法、模糊数学分析法、粗糙理论分析法、遗传算法、神经网络分析法、矩母函数法、Petri网行为表达式法、计算树逻辑、灰度分析法等等。这些分析技术大都依据被分析系统的特点而设定,其中神经网络方法结合神经网络的学习算法,可通过对样本数据学习来调整模型中的参数,以获得系统内部的等效结构,从而达到计算出非样本数据的可靠度,这种方法是使得Petri网模型具备学习能力的一个重要手段。除此之外,Petri网行为表达式法和矩母函数法将PN机的行为理论与传统Petri网建模技术结合在一起,可以有效地解决一般Petri网状态可达图难以获得和状态空间爆炸的问题。
Petri网的模拟工具有好几十种,其中不仅有支持P/T网、有色Petri网、时间Petri网、随机Petri网、排队Petri网等类型,一些近年来获得研究关注的复杂Petri网,如混杂Petri网、抑制Petri网也有了相应的模拟工具,如带时间元素的层次颜色Petri网工具CPN Tools、带时间元素的随机Petri网工具F-net、带时间元素的混杂Petri网工具HISIm、层次排队Petri网工具QPME等等,但是可惜的是时序Petri网还未见有相应的模拟工具。这些模拟工具一般都含有以下3个方面的功能:1)图形化的编辑界面,定义了库所、变迁、弧以及其他函数的图形框架;2)计算机动态模拟过程,可以动态地显示被考察系统当前所处的随机状态,以及显示系统在仿真运行过程中产生的可达图或者折叠可达图信息;3)性能分析和评价功能,可以对用户定义的性能指标进行计算。在实际的系统分析或建模过程中,建模者可以根据系统的特点和平台的使用对语言进行有选择地使用。
Petri网模型具有强的可视性,且可动态演示系统运行过程,这是其他模型(例如故障树、FMEA等)所做不到的。例如,对于冗余系统及可修系统,难于应用故障树进行建模。而可修系统由于系统状态是离散的,系统及系统中部件的失效及修复是随机且相依的,是一个典型的离散动态系统,可通过Petri网加以描述和分析。目前应用较多的是利用Petri网的逻辑描述能力代替故障树进行系统可靠性分析建模,可将故障树模型转换为相应的Petri网模型。根据得到的Petri网能够写出关联矩阵,通过关联矩阵,能够快速得到故障树的最小割集。
建模步骤如图3-19所示:
1) Petri网模型构建:需要对复杂系统的可靠性功能逻辑关系进行分析,建立系统随机有色Petri网模型;
2)可靠性仿真算法。即利用节点排序算法对建立的Petri网模型获取Petri网链接顺序表,再利用蒙特卡洛仿真进行N次仿真;
3)可靠性指标计算:即以蒙特卡洛仿真为基础,通过对Petri网模型中的库所、变迁状态(变迁是否发生)进行统计,获得系统可靠度等指标。

图3-19可靠性PN模型分析流程