




贝叶斯定理为:如果I是依赖于两个相互排斥事件H与J之一的事件,H与J必有一个发生,则I发生的概率为: P ( I )= P ( I | H ) P ( H )+ P ( I | J ) P ( J )。应用贝叶斯定理可以给出系统失效的概率,则系统可靠度为: R =1- P 。
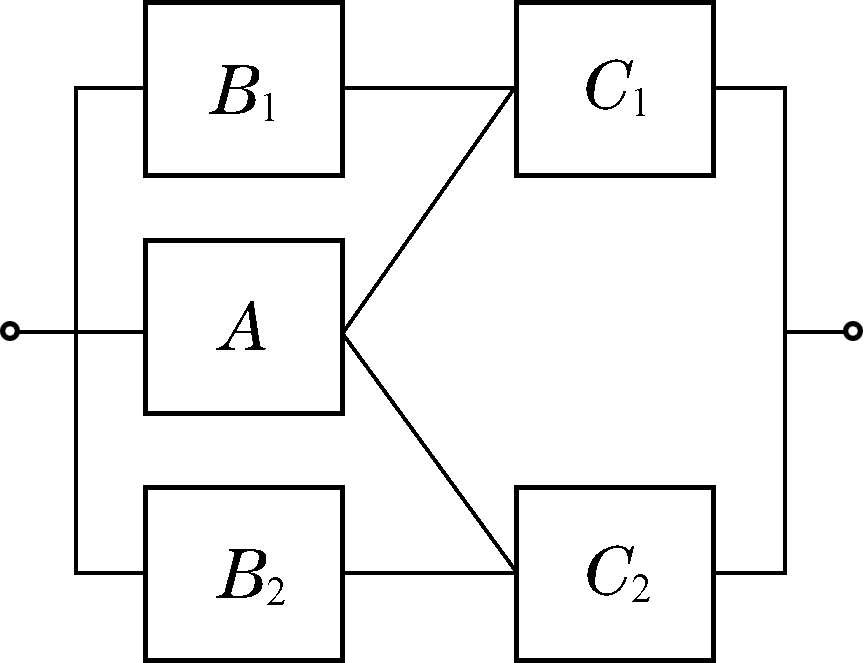
图3-16较复杂的可靠性结构模型
应用贝叶斯定理对图3-10所示的可靠性模型可以给出系统失效的概率。
P(系统失效)=P(系统失效|A好)P(A好)+P(系统失效|A坏)P(A坏)
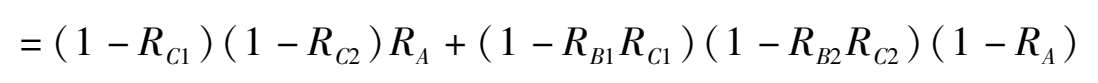
如果 R B1 = R B2 =0.1, R C1 = R C2 =0.2, R A =0.3,则 R =1- P (系统失效)=0.135 72。
对于如图3-16所示的较为复杂的可靠性结构模型,可用贝叶斯法进行计算。贝叶斯法较为简单,可以用一般概率知识和简单的可靠性结构进行简化计算。
[例3-1] 用贝叶斯法对图3-10所示的桥式可靠性结构模型进行求解。
当Q好时,系统变为“并串联”状态;当Q坏时,系统变为“串并联”状态。根据贝叶斯定理,系统的不可靠度为: F =[1-(1- F 1 F 2 )(1- F 3 F 4 )] R Q +(1- R 1 R 3 )(1- R 2 R 4 ) F Q 。
贝叶斯网络又称信度网络,是目前不确定知识表达和推理领域最有效的理论模型之一,是贝叶斯方法的扩展,贝叶斯网络已经成为近几年来研究的热点。由于贝叶斯网络具有强大的模型描述能力和推理能力,使其在数据挖掘、模式识别、故障诊断、生态评估、医疗诊断以及环境管理等方面获得了较为广泛的应用。目前,贝叶斯网络理论研究以及在可靠性分析中的应用也越来越受到国内外学者的重视。 Bobbio,Boudali,Montani等提出了故障树向动态贝叶斯网络的映射方法,这一方法的提出为解决动态系统、可维修系统的可靠性分析开拓了新的思路。