




自然数 N :0,1,2,…
整数包括正整数、负整数和零。两个整数的和、差、积仍是整数,但是用一个不等于零的整数去除另一个整数所得的商不一定是整数。表示方式 Z :…,-2,-1,0,1,2,…
数的整除:当整数
a
除以非零整数
b
,商正好是整数而无余数时,则称
a
能被
b
整除或
b
能整除
a
,记作
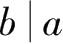 .
.
倍数、约数:当 a 能被 b 整除时,称 a 是 b 的倍数, b 是 a 的约数.
常见的整除:
被2整除的数,偶数(个位是0,2,4,6,8).
被3整除的数,各位数字之和必能被3整除.
被4整除的数,末两位(个位、十位)必能被4整除.
被5整除的数,个位为0或者5.
被9整除的数,各位数字之和必能被9整除.
被12整除的数,同时满足能被3和4整除的条件.
百分数
:设两个整数
a
,
b
,若整数
p
满足
 ,则称
p
是
a
,
b
的一个公因数。整数
a
,
b
的公因数中最大的那个叫作
a
,
b
的最大公因数,记为(
a
,
b
).
,则称
p
是
a
,
b
的一个公因数。整数
a
,
b
的公因数中最大的那个叫作
a
,
b
的最大公因数,记为(
a
,
b
).
百分数
:设两个整数
a
,
b
,若整数
p
满足
 ,则称
p
是
a
,
b
的一个公倍数。整数
a
,
b
的公倍数中最小的那个叫作
a
,
b
的最小公倍数,记为[
a
,
b
].
,则称
p
是
a
,
b
的一个公倍数。整数
a
,
b
的公倍数中最小的那个叫作
a
,
b
的最小公倍数,记为[
a
,
b
].
百分数 :如果一个大于1的正整数,只能被1和它本身整除(只有1和其本身两个约数),那么这个正整数叫作质数(质数也称素数)。互质数:公约数只有1的两个数称为互质数,如9和16.
百分数 :一个正整数除了能被1和它本身整除外,还能被其他的正整数整除(除了1和其本身之外,还有其他约数),这样的正整数叫作合数.
质数与合数有如下重要性质:
1.质数和合数都在正整数范围内,且有无数多个.
2.2是唯一的既是质数又是偶数的整数,即是唯一的质偶数。大于2的质数均为奇数。质数中只有一个偶数2,最小的质数为2.
3.若质数
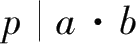 ,则必有
,则必有
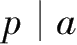 或
或
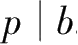 . (注:
. (注:
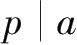 表示p是a的约数)
表示p是a的约数)
4.若正整数 a , b 的积是质数 p ,则必有 p = a 或 p = b .
5.1既不是质数也不是合数.
6.如果两个质数的和或差是奇数,那么其中必有一个是2;如果两个质数的积是偶数,那么其中也必有一个是2.
7.最小的合数为4.任何合数都可以分解为几个质数的积,能写成几个质数的积的正整数就是合数.
百分数 :不能被2整除的数 . n =2 k +1, k 是任意整数.
百分数 :能被2整除的数 . n =2 k , k 是任意整数。注意,0是偶数.
注意
1.两个相邻整数必为一奇一偶。除了最小质数2是偶数外,其余质数均为奇数.1既不是质数,也不是合数.
2.奇数、偶数在运算中的法则:
奇数×奇数=奇数偶数×偶数=偶数偶数×奇数=偶数
奇数+奇数=偶数偶数+偶数=偶数偶数+奇数=奇数
一般地,设 a , b 为整数,那么 a + b 与 a - b 具有相同的奇偶性.
百分数 :将单位1平均分成若干份,表示这样的一份或几份的数叫作分数.
百分数 :表示一个数是另一个数的百分之几的数叫作百分数,通常用“%”来表示.
整数和分数统称有理数。任何一个有理数都可以写成分数
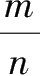 的形式(
m
,
n
均为整数,
n
≠0).因为分数与有限小数和无限循环小数可以互化,所以又称有理数为有限小数和无限循环小数。若(
m
,
n
)=1,则称
的形式(
m
,
n
均为整数,
n
≠0).因为分数与有限小数和无限循环小数可以互化,所以又称有理数为有限小数和无限循环小数。若(
m
,
n
)=1,则称
 为既约分数.
为既约分数.
有理数运算具有封闭性,两个有理数的和、差、积、商(分母不为0)仍然是一个有理数.
两个数相除,又称为这两个数的比,即
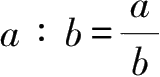 .其中
a
叫作比的前项,
b
叫作比的后项。若
a
除以
b
的商为
k
,则称
k
为
a
∶
b
的比值.
.其中
a
叫作比的前项,
b
叫作比的后项。若
a
除以
b
的商为
k
,则称
k
为
a
∶
b
的比值.
如果两个比
a
∶
b
和
c
∶
d
的比值相等,就称
a
、
b
、
c
、
d
成比例,记作
a
∶
b
=
c
∶
d
或
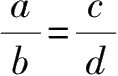 ,其中,
a
和
d
叫作比例外项,
b
和
c
叫作比例内项.
,其中,
a
和
d
叫作比例外项,
b
和
c
叫作比例内项.
性质和定理:
1 .a ∶ b = c ∶ d ⇔ ad = bc. ( 交叉相乘等积 ).
2 .a ∶ b = c ∶ d ⇔ b ∶ a = d ∶ c ⇔ b ∶ d = a ∶ c ⇔ d ∶ b = c ∶ a ( 交叉换位 ).
3.
合比定理
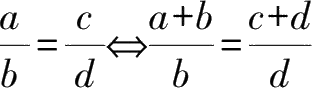 .
.
4.
分比定理
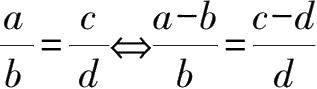 .
.
5.
合分比定理
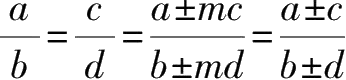 (m
=1).
(m
=1).
6.
等比定理
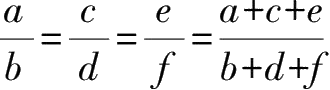 (b
+
d
+
f
≠0).
(b
+
d
+
f
≠0).
若 y = kx ( k 不为零),则称 y 与 x 成正比, k 称为比例系数.
若
y
=
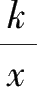 (
k
不为零),则称
y
与
x
成反比,
k
称为比例系数.
(
k
不为零),则称
y
与
x
成反比,
k
称为比例系数.
1.无理数:无限不循环小数,如
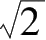 、
、
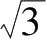 、e、π等.
、e、π等.
2.无限不循环小数被称为无理数。有理数和无理数统称实数.
3.任意两个实数的和、差、积、商(除数不等于零)仍是实数.
4.对于任意实数 x ,用[ x ]表示不超过 x 的最大整数;令[ x ]= x -{ x },称[ x ]是 x 的整数部分,{ x }是 x 的小数部分.
数的分类:

百分数
:
a
、
b
为有理数,
α
为无理数,由
a
+
bα
=0⇒
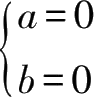 .
.
1.绝对值:
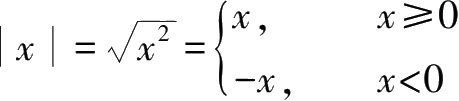 .
.
2.设
x
1
,
x
2
,…,
x
n
为
n
个数,称
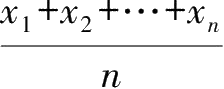 为这
n
个数的算术平均值,记为
为这
n
个数的算术平均值,记为
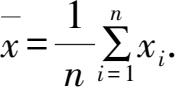
3.设
x
1
,
x
2
,…,
x
n
为
n
个正实数,称
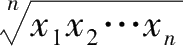 为这
n
个数的几何平均值,记为
为这
n
个数的几何平均值,记为
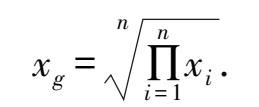
4.性质:
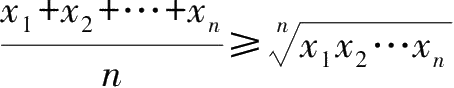 ,当且仅当
x
1
=
x
2
=…=
x
n
时等号成立.
,当且仅当
x
1
=
x
2
=…=
x
n
时等号成立.
1.非零数的零次方幂都等于1 .x 0 =1( x ≠0).
2.任何数的1次方幂都等于它本身 . x 1 = x.
3.同底数幂相乘,底数不变指数相加 . x a · x b = x a + b .
4.指数的乘方等于底数不变指数相乘.( x a) b = x ab .
5.积的乘方等于乘方的积.( xy ) a = x a y a .
6.负指数幂等于正指数幂的倒数.
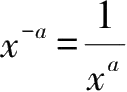 .
.
7.
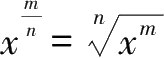 (
x
≥0).
(
x
≥0).
8.
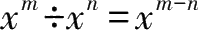 .
.
9.
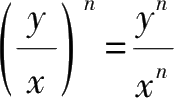 (
x
≠0).
(
x
≠0).
10.
 .
.
一般地,形如
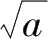 (
a
≥0)的代数式叫作二次根式。根号下含有字母、且不能够开得尽方的式子称为无理式.
(
a
≥0)的代数式叫作二次根式。根号下含有字母、且不能够开得尽方的式子称为无理式.
二次根式的非负性:
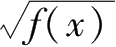 中必有
f
(
x
)≥0且
中必有
f
(
x
)≥0且
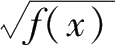 ≥0.
≥0.
形如
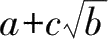 与
与
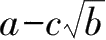 的两个二次根式,叫作共轭根式.
的两个二次根式,叫作共轭根式.
若 a , b , c 是有理数,则共轭根式的和、积都是有理数.
若 a , b , c 是整数,则共轭根式的和、积都是整数.
常用于分母(分子)有理化。如:
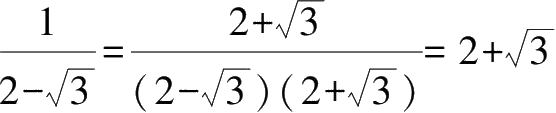 .
.

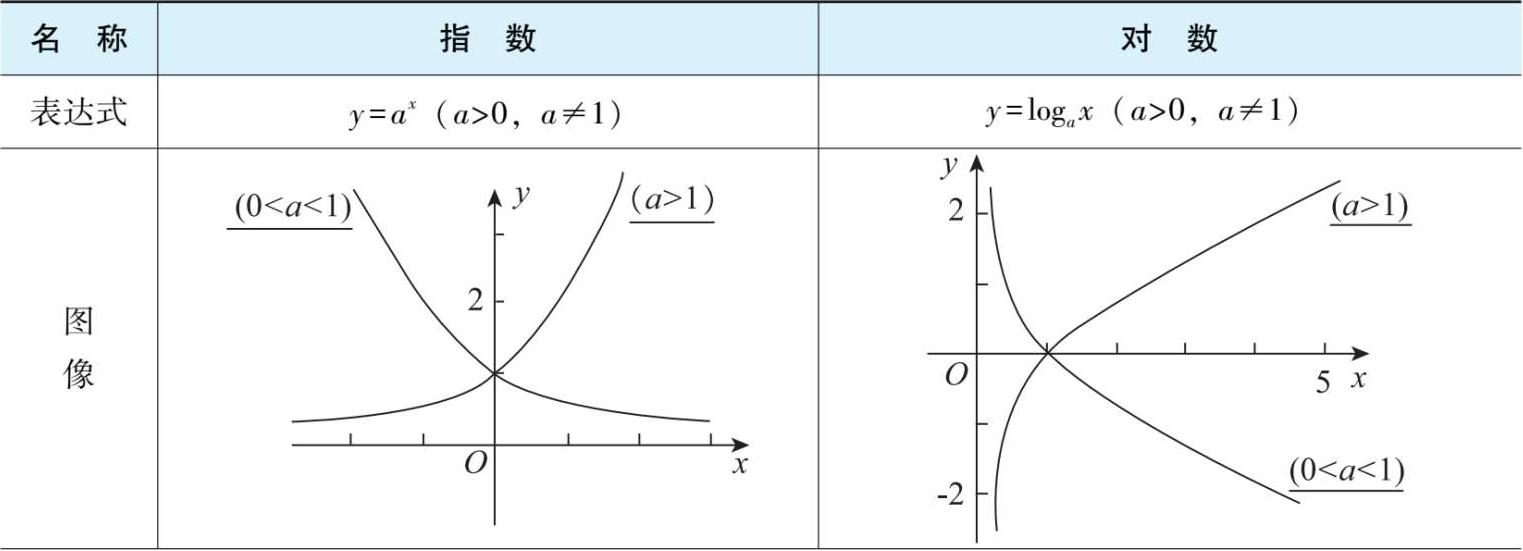
(续)
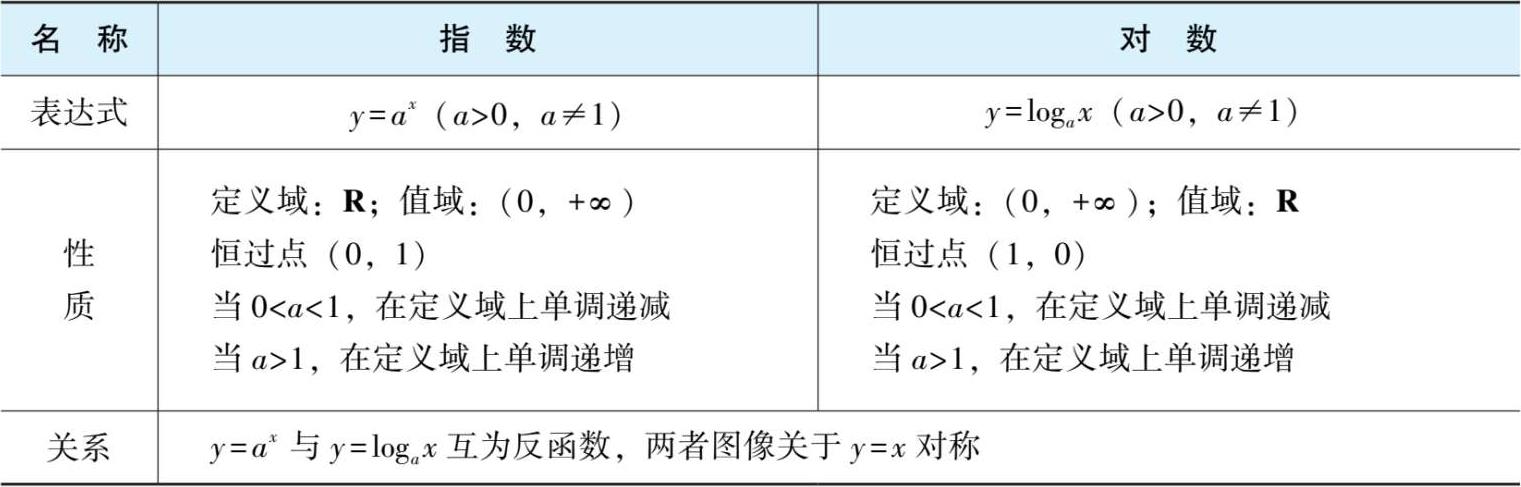
在日常生活和工作中,人们需要经常对数据进行分析和统计描述,最常见的数据统计描述内容是计算数据分布的中心值和离散度.
数据分布的中心值是指最能代表样本数据的典型值。中心值有多种定义,最常用的是平均值。离散度反映样本数据是集中分布在中心值附近,还是相对于中心值数据分布比较分散,变化较大。衡量数据分布离散度的最常用的参数是方差和标准差.
1.有
n
个数
x
1
,
x
2
,…,
x
n
,称
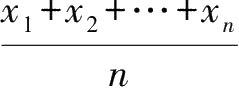 为这
n
个数的算术平均值,记为
为这
n
个数的算术平均值,记为
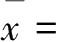
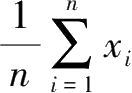 ,在统计中,算术平均值常被称为平均数.
,在统计中,算术平均值常被称为平均数.
2.有
n
个正实数
x
1
,
x
2
,…,
x
n
,称
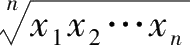 为这
n
个数的几何平均值,记为
为这
n
个数的几何平均值,记为
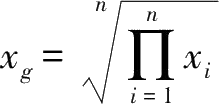 .
.
1.给出一组样本数据:
x
1
,
x
2
,…,
x
n
.方差是各样本数据值与所有样本数据值的平均值之差的平方的平均数。其中任意一个样本数据值与所有样本数据的平均数的差
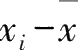 (
i
=1,2,…,
n
),叫作这个样本数据
x
i
的离差,故一组样本数据的方差是这组数据的所有离差平方的算术平均值,它是反映这组数据分布偏离其平均数的平均指标。其方差表达式为:
(
i
=1,2,…,
n
),叫作这个样本数据
x
i
的离差,故一组样本数据的方差是这组数据的所有离差平方的算术平均值,它是反映这组数据分布偏离其平均数的平均指标。其方差表达式为:
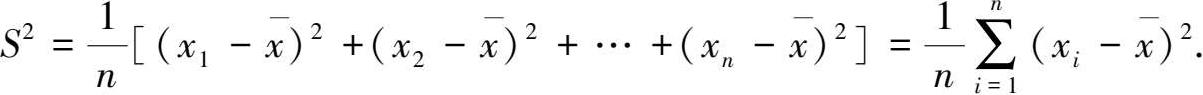
2.方差的算术平方根称为标准差 S. 如果样本数据是有单位的量,则标准差也是一个有相同单位的量。它比方差更能反映这组数据分布偏离其平均数的程度。其表达式为:
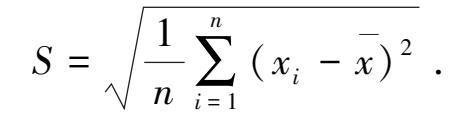
方差和标准差是衡量一组样本数据分布的离散度的量。它们的值越小,该组数据分布的离散程度越小,数据的分布也就相对稳定.
众数 :在一组给出的数据中,出现次数最多的数称为众数.
中位数 :给出的一组数据,将数据由小到大排列,若有奇数个数据,则正中间的数为中位数;若有偶数个数据,则中位数为中间两个数的平均数.
在有理式中没有除法运算或有除法运算但除式中不含字母的式子叫作整式。整式包括单项式和多项式。整式的和、差、积仍是整式.
设 n 是一个非负整数, a 0 , a 1 , a 2 ,…, a n 都是实数,多项式 a n x n + a n -1 x n -1 +…+ a 1 x + a 0 被称为实系数多项式。若 a n ≠0,则称为一元 n 次实系数多项式,简称为 n 次多项式。我们用 f ( x ), g ( x ),…代表多项式。例如: f ( x )=2 x 3 - x 2 +1是一个三次多项式, g ( x )= x 2 +1是一个二次多项式, h ( x )=6是一个零次多项式(零次多项式就是只有常数项 a 0 ≠0的单项式).
两个多项式 f ( x )= a n x n + a n -1 x n -1 +…+ a 1 x + a 0 , g ( x )= b m x m + b m -1 x m -1 +…+ b 1 x + b 0 的和、差、积仍是一个多项式,但两个多项式的商不一定是一个多项式。因此,整除就成了两个多项式之间的一种特殊关系.
整式 F ( x )除以整式 f ( x )商式为 g ( x ),余式为 r ( x ),则有 F ( x )= f ( x )· g ( x )+ r ( x ).
当 r ( x )=0时, F ( x )= f ( x )· g ( x )成立,此时则称整式 F ( x )能被整式 f ( x )整除.
整式 F ( x )除以 x - a 的余式为 r ( x ),则 F ( x )=( x - a )· g ( x ) + r ( x ),故 r ( a )= F ( a )成立.
把一个多项式表示成几个整式之积的形式,叫作多项式的因式分解。常用方法如下:
方法一:提取公因式.
方法二:求根法。若方程 a n x n + a n -1 x n -1 +…+ a 1 x + a 0 =0有 n 个根 x 1 , x 2 ,…, x n ,则多项式
a n x n + a n -1 x n -1 +…+ a 1 x + a 0 = a n ( x - x 1 )( x - x 2 )…( x - x n ).
方法三:二次三项式的十字相乘法.
方法四:待定系数法.
常用的公式
1 .a 2 - b 2 =( a + b )( a - b ).
2.( a ± b ) 2 = a 2 ±2 ab + b 2 .
3.( a ± b ) 3 = a 3 ±3 a 2 b +3 ab 2 ± b 3 .
4 .a 3 - b 3 =( a - b )( a 2 + ab + b 2 ).
5 .a 3 + b 3 =( a + b )( a 2 - ab + b 2 ).
6.( a + b + c ) 2 = a 2 + b 2 + c 2 +2 ab +2 bc +2 ac.
7
.a
2
+
b
2
+
c
2
-
ab
-
ac
-
bc
=
 [(
a
-
b
)
2
+(
b
-
c
)
2
+(
c
-
a
)
2
].
[(
a
-
b
)
2
+(
b
-
c
)
2
+(
c
-
a
)
2
].
8
.a
3
+
b
3
+
c
3
-3
abc
=
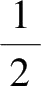 (
a
+
b
+
c
)[(
a
-
b
)
2
+(
b
-
c
)
2
+(
c
-
a
)
2
].
(
a
+
b
+
c
)[(
a
-
b
)
2
+(
b
-
c
)
2
+(
c
-
a
)
2
].
1.用一次多项式 x - a 去除多项式 f ( x ),所得的余式是一个常数,这个常数值等于函数值 f ( a ).即设 f ( x )= a n x n + a n -1 x n -1 +…+ a 1 x + a 0 ,则 f ( a )= a n a n + a n -1 a n -1 +…+ a 1 a + a 0 ,得 f ( x )= q ( x )( x - a )+ f ( a ).
2 .a 是 f ( x )的根的充分必要条件是( x - a ) f ( x ).
3.带余除法(综合除法)
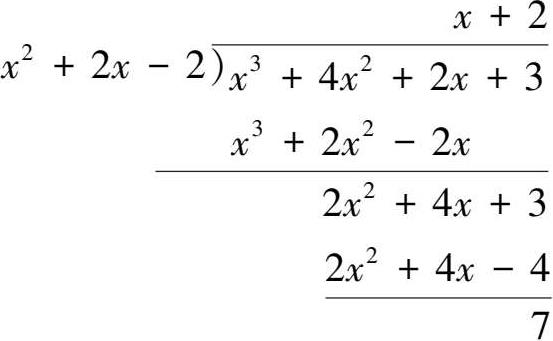
用
A
,
B
表示两个整式,
A
÷
B
就可以表示成
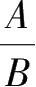 的形式。如果
B
中含有字母,则称
的形式。如果
B
中含有字母,则称
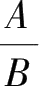 为分式,其中
A
叫作分式的分子,
B
叫作分式的分母.
为分式,其中
A
叫作分式的分子,
B
叫作分式的分母.
1.分式的加减运算。同分母的几个分式相加减,分母不变,分子相加减,注意最后结果要约分化为最简分式。不同分母的几个分式相加减,取这几个分式分母的公分母作分母,通分后化为同分母分式的加减运算。例如:
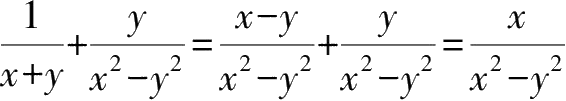 .
.
2.分式的乘除运算。几个分式相乘,分子乘分子,分母乘分母,注意约分。分式的乘法运算满足交换律、结合律和分配律。例如:
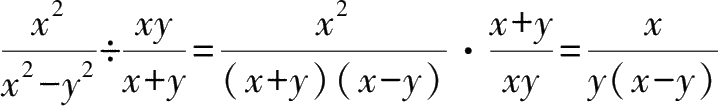 .
.
3.注意:(1)分式有意义的条件:分母不等于零;
(2)分式无意义的条件:分母等于零;
(3)分式的值等于零的条件:分子等于零且分母不等于零.
常用经验公式:
1.1+2+3+…+
n
=
 n
(
n
+1).
n
(
n
+1).
1
2
+2
2
+3
2
+…+
n
2
=
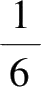 n
(
n
+1)(2
n
+1).
n
(
n
+1)(2
n
+1).
1
3
+2
3
+3
3
+…+
n
3
=
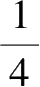 n
2
(
n
+1)
2
=(1+2+3+…+
n
)
2
.
n
2
(
n
+1)
2
=(1+2+3+…+
n
)
2
.
2.
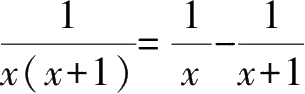 .
.
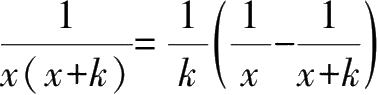 .
.
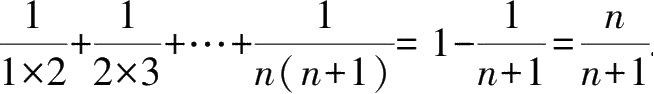 .
.
3.
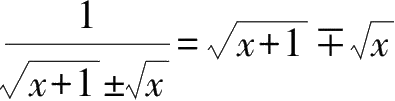 (分母有理化).
(分母有理化).
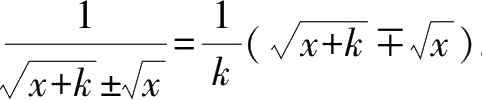 .
.