




在现实生活中,绝大多数人都具备图的思维方式吗?我们来一起看看这个问题:构造一张图(由顶点、边构成的图),假设图中有5个三角形,只增加1条边,就让三角形的个数增加到10,请画出这张图的结构。
先决条件:在这张图中,顶点为账户,边为账户间的交易,账户间可以有多笔交易。所谓的三角形为三个账户间的转账交易形成的原子级的三角形,原子级的意思是三角形不可嵌套,三角形中每条边都是原子级的,不可分割,例如1条边仅对应1笔转账交易。
让我们来分析一下这个题目的关键点:只增加1条边,三角形却要增加5个。也就是说,先前有5个三角形,它们若共享了1条待增加的边后,就会形成5个新的三角形,而之前的5个三角形到底怎么样根本不重要。共享新的边,意味着这5个三角形也会共享共同的两个顶点。分析至此,答案是不是呼之欲出了?
这是一道笔者从真实的业务场景中提炼出来的面试题。对于擅长百度或谷歌搜索以及刷题的应试者,这道题会让很多人手足无措。90%技术岗位的应试者在网上面试阶段看到这道题之后都归于沉默了。
9%的人给出了如图1-9所示的答案:很显然这个答案中的竖线实际上引入了多条边、多个顶点,它并不符合只增加1条边的条件,而且会破坏之前的(原子的、不可拆分的)三角形或边的定义。大抵给出这种答案的人都没有仔细读题。
这个问题最好的地方在于,它可以有很多个答案,不一而足。例如图1-10所示的这个答案,这样构图可谓用心良苦,虽然略显复杂,但在本质上完全符合上面的分析:固定两个顶点,连上一条边,出现了5个新的三角形。
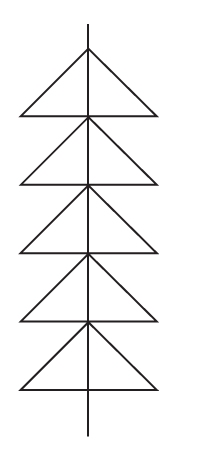
图1-9 应试人员解题答案(一)
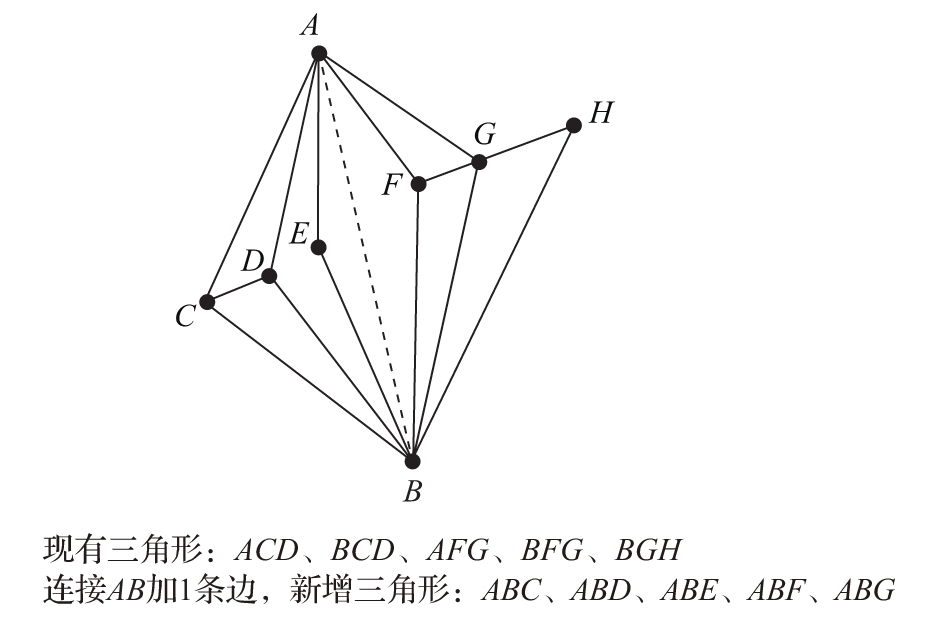
图1-10 应试人员解题答案(二)
那么更简洁的方案是什么样的呢?如图1-11所示的是7个顶点(A~G)之间已经形成了5个三角形,在AB之间如果再新增1条边,则7个顶点间就形成了10个三角形。为了在二维平面内表达这个高维空间,我们用虚线表示被遮盖部分的边。
很显然,这个方案用了较少的点和边。它最棘手的地方在于在顶点AB之间新增的边,很多人觉得不可思议,但是如果仔细读问题中的先决条件,A、B是两个账户,账户之间可以存在多笔交易,这个其实已经在暗示读者解题的思路了。
那么,按照这个思路继续探寻下去,如何构造一个使用最少的点和边的图来解之前的题目呢?
如图1-12所示的解决方案是仅使用4个顶点与7条边构成的5个三角形。增加了边8之后,形成了5个新的三角形。这个解法中最巧妙之处是在顶点A、C、B之间由1~5号边所形成的4个三角形复用了1、2、3、4这几条边。
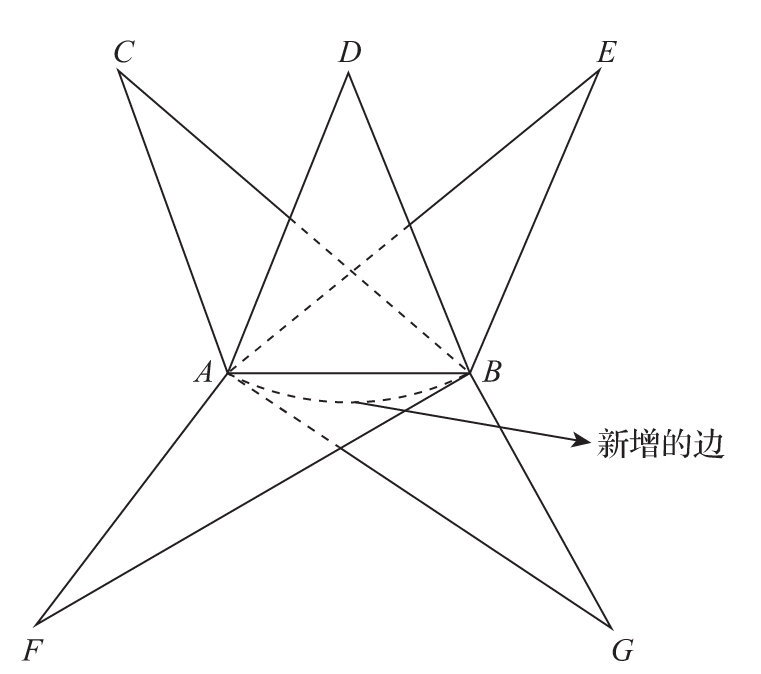
图1-11 应试人员解题答案(三)
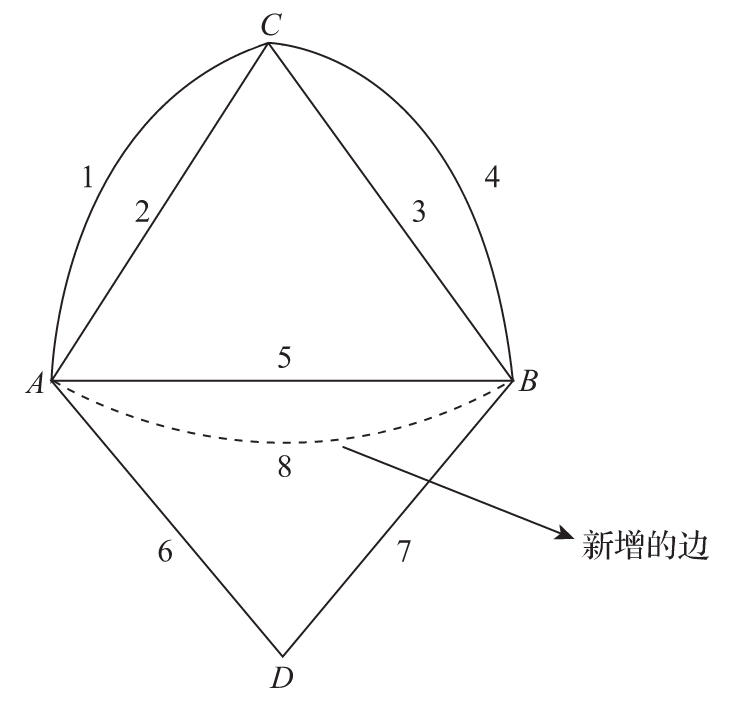
图1-12 应试人员解题答案(四)
目前已知的最精简的构图如图1-13所示,它只用了“3个顶点+8条边”。聪明的读者如果想到更极致的方案,欢迎联系笔者。
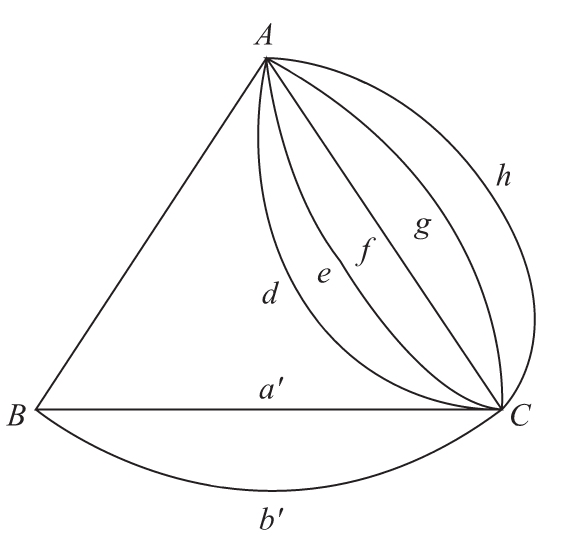
图1-13 应试人员解题答案(五)
现在让我们探究一下这个题目背后所蕴含的图的意义。在银行业中,以零售转账为例,在大型的银行中有数以亿计的借记卡账户,这些账户每个月有数以亿计的交易(通常交易的数量会数倍于账户数量),如果以卡账户为顶点,账户间的交易为边,就构成了一张数以亿计的点边的大图。如何衡量这些账户之间的紧密程度呢?或者说如何去判断这张图的拓扑空间结构呢?类似地,在一张SNS的用户社交网络图中,顶点为用户,边为用户间的关联关系,如何衡量这张社交图谱的拓扑结构或紧密程度呢?

图1-13 应试人员解题答案(五)
三角形是表达紧密关联关系的最基础的结构。如图1-14的社交网络图谱(局部)所示,两个框内的4个顶点间都构成了16个(2×2×2+2×2×2)三角形。从空间结构上看,它们之间的紧密程度也更突出。
上面提到的银行转账账户间所形成的三角形关系的个数,在很大程度上可以表达银行账户之间的某种关联关系的紧密程度。某股份制银行的账户间在2020年某三个月中转账数据形成了2万亿个三角形,而顶点与边的个数都在10亿以内,也就是说平均每个顶点都参与到了上千个转账三角形关系中。这个数字是非常惊人的,例如A、B、C三个顶点,两两之间存在100条边,那么它们总共就构成了100万个三角形关系。类似地,A与B两个顶点之间存在一条关系,它们各自分别与另外1000个账户存在转账关系,这时只要AB之间再增加1条边,图上就会增加1000个三角形,每增加一条AB之间的边就会增加至少1000个三角形。是不是有一点神奇?
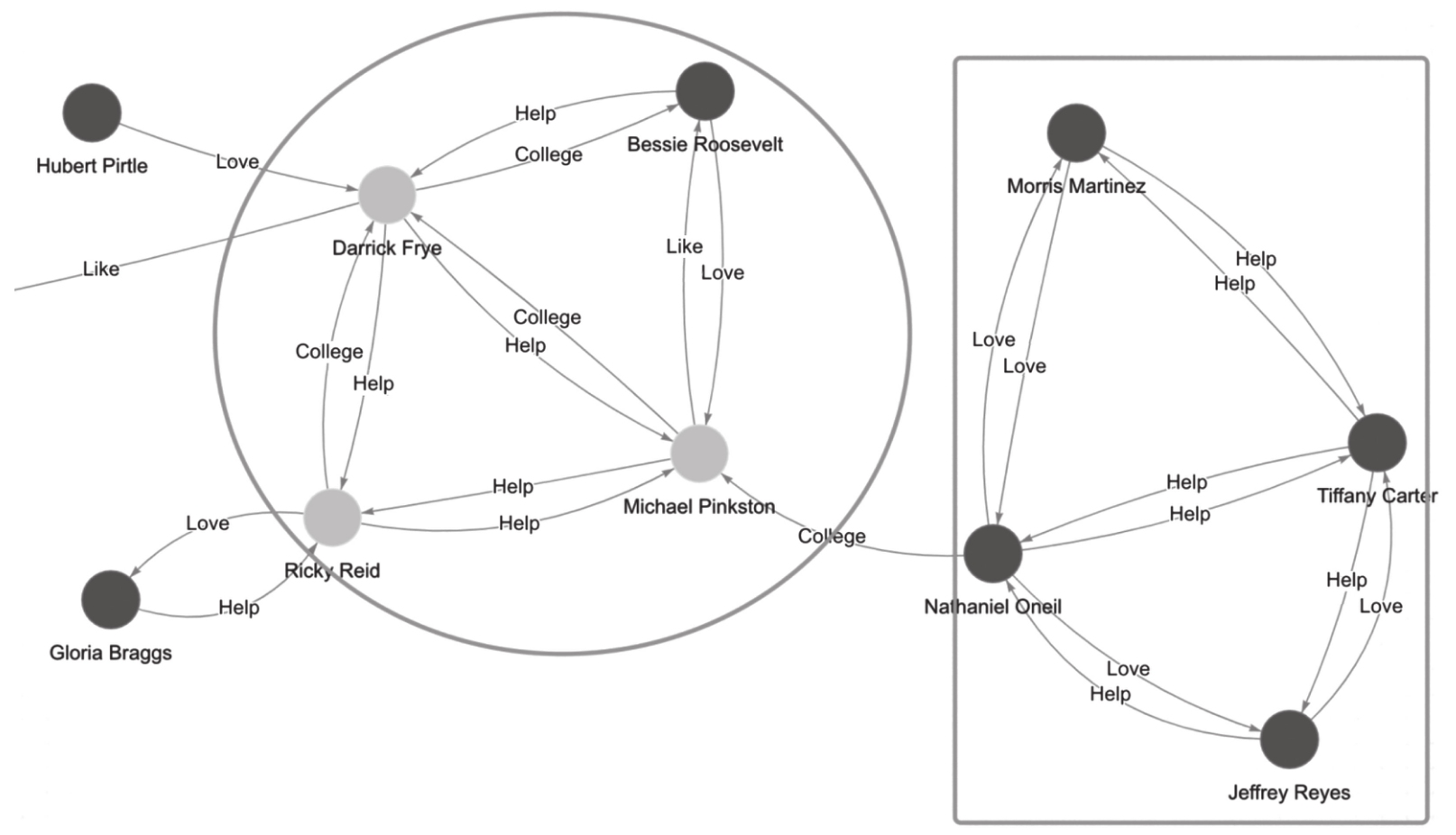
图1-14 社交网络图谱(局部)
当然,无论是转账交易数据、社交网络数据、电商交易数据还是信用卡交易数据,数据所形成的网络(图),用数学语言来定义就是一个拓扑空间。在这个拓扑空间中,我们关心的是数据之间的关联性、连通性、连续性、收敛性、相似度(哪些节点的行为、特征更为相似)、中心度、影响力,以及传播的力度(深度、广度)等。用拓扑空间内数据关联的方法来构造的图可以100%还原并反映真实世界中我们是如何记录并认知世界的。如果一个拓扑空间(一张图)不能满足对异构数据的描述,就构造另一张图来表达。每一张图可以看作从一个(或多个)维度或领域(如知识领域、学科知识库等)对某个数据集的聚类与关联,区别于传统关系型数据库的二维关系表的方式,每一张图可以是多个关系表的有机关联组合。
在图上不再需要传统的关系表操作中的表连接操作,而用图上的路径或近邻类操作取代。我们知道表连接的最大问题是不可避免地会出现笛卡儿乘积的挑战,尤其是在大表中,这种乘积的计算代价极大,参与表连接的表越多,它们的乘积就越大(如3个表X、Y、Z,它们的笛卡儿乘积的计算量是{X}*{Y}*{Z},如果X、Y、Z各有100万、10万、1万行,计算量是1000万亿)。在很多情况下,关系型数据库批处理缓慢的一个主要原因就是需要处理各种多表连接的问题。我们说这种低效性实际上是因为关系型数据库(以及它配套的查询语言SQL)没有办法在数据结构层面做到100%反映真实世界。
人类大脑的存储与计算从来不会在遍历和穷举甚至笛卡儿乘积上浪费时间,但是当我们被迫使用关系型数据库以及Excel表格的时候,经常需要极为低效地做反复遍历和乘积的事情,在图上则不会出现这种问题——在最坏的情况下,你可能需要以暴力的方式在图上遍历一层又一层的邻居,但是它的复杂度依然远远低于笛卡儿乘积(例如1张图有1000万个点和边,遍历它的复杂度最大则为1000万——任何高于其最大点和边数量的计算复杂度都是数据结构、算法或系统架构设计败笔的体现)。
在上一节中,我们提到了一个关键的概念、愿景:图数据库是终极的数据库,所有人工智能的终极归宿就是强人工智能,也就是具有人的智能。而我们可以确定的是,人的思维方式就是100%图的思维方式,而可以比拟、还原人的思维方式的图数据库或图计算的方式称为原生图(native graph)。通过原生图的计算与分析,我们可以让机器具备人类一样的高效关联、发散、推导、迭代的能力。
所谓原生图,是相对于非原生图而言的,在本质上指的是图数据如何以更高效的方式进行存储和计算。非原生图采用的可能是关系型数据库、列数据库、文档数据库或键值数据库来存储图数据;而原生图需要使用更高效的存储(及计算)方式来为图计算与查询服务。
原生图首先构建的是数据结构,这里要引入一个新的概念——无索引近邻(index-free adjacency)。这个概念既和存储有关,又和计算相关。在第2章中我们会详细地介绍这种数据结构。在这里,简而言之,无索引近邻数据结构相对于其他数据结构的最大优势是在图中访问任一数据所需的时间复杂度为O(1)。例如,从任一数据点出发去访问它的1度近邻的时间复杂度也是O(1),反之亦然。而这种最低时间复杂度的数据访问恰恰就是人类在大脑中搜寻任何知识点并关联发散出去时所采用的方式。这种数据结构显然和传统数据库中常见的基于树状索引的数据结构不同,从时间复杂度上看是O(1)与O(log N)
的区别,而在更复杂的查询或算法实现中,这种区别会放大为O(K)与O(N log N)或者更大的差异性(K≥1,通常小于10或20,但一定远远小于N,假设N是图中顶点或实体的数量)。这就意味着在复杂运算的时效性上会有指数级的区别,图上如果是1秒钟完成,传统数据库则可能需要1个小时、1天或者更久(或者无法完成)来完成,这意味着传统数据库或数据仓库中的那些动辄T+1的批处理操作可以以T+0甚至纯实时的方式瞬间完成。
当然,数据结构只是解决问题的一个方面,我们还需要从体系架构(例如并发、高密度计算)、算法并发优化、代码工程优化等多个维度让(原生)图数据库真的腾飞。有了原生图存储与高并发、高密度计算在底层算力上的支撑,图上的遍历、查询、计算与分析可以得到进一步的飞跃。如果传统的图数据库比关系型数据库快1000倍,那么飞跃之后的图要快100万倍。