




修完学校提供的数学课程之后,在高中的最后一年,我与乔夫里先生分开了,并且开始自学。我每天花一小时独自坐在空荡的教室里,阅读关于多元微积分的书,或者探索惠更斯摆钟之谜。其他时间我用来做研究,通常都是关于追逐问题的。我完全被这类数学家称为“追及”(pursuit)的问题迷住了。
我第一次知道追及问题是在乔夫里先生的课堂上。问题是这样的:
假设一个邮递员正在尝试摆脱一条追着他跑的狗。邮递员从原点 O 出发,然后以匀速 v 沿着直线跑。与此同时,那条狗从直线外的某一点出发,以匀速 w 跑向直线,到达直线后突然改变方向,使它总能直奔邮递员当前所在的位置,请列出这条狗的追逐曲线方程(见图2-1)。
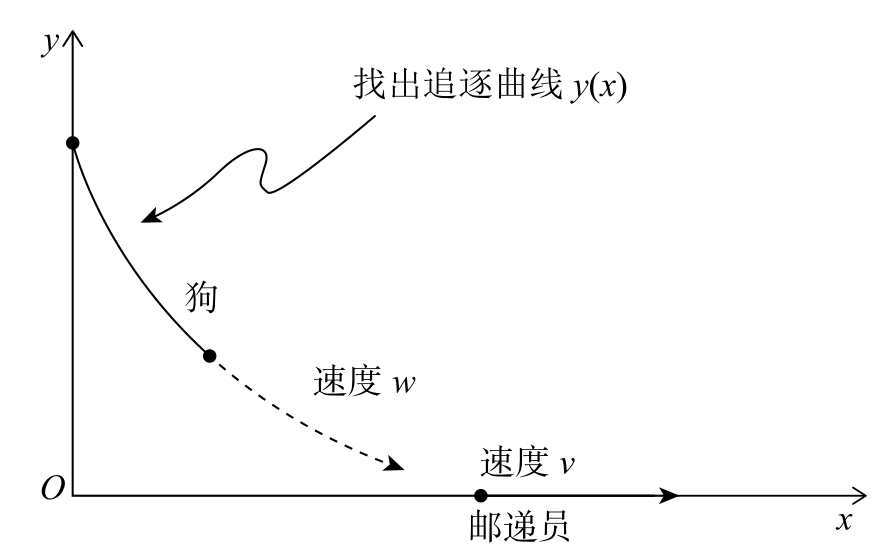
图2-1
还有一道追及问题更具有乔夫里的特色:
一个皮划艇运动员正在奋力划向对岸的某处。划皮划艇的人是那种目标坚定但头脑简单的人,总是直奔目的地,即使河流正把他冲向下游也是如此。假设河水水流速度是常数 v ,皮划艇运动员以相对于水流的常速 w 划行,请给出皮划艇的运动路径(见图2-2)。
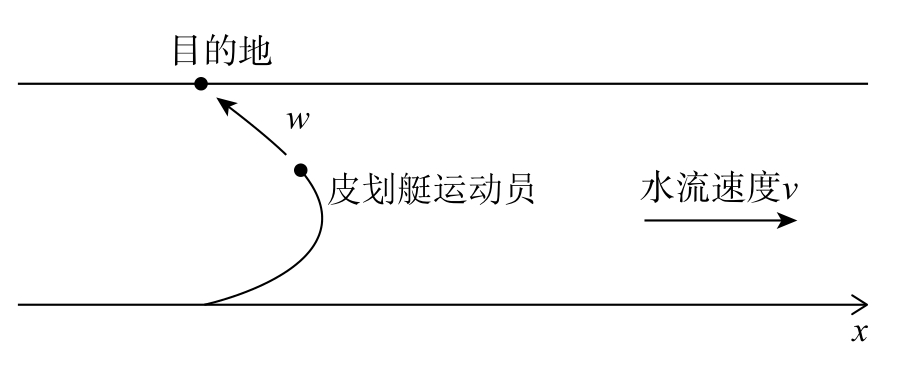
图2-2
这两个追及问题,一个是关于小狗和邮递员的,另一个是关于一心想划到对岸的皮划艇运动员的,都是微分方程的练习题。这些都是关于微积分的方程,关于通量和变化。微分方程描述的是系统如何根据作用于它的力的不断变化而改变自己。所有这些推力和拉力都让系统处于新的条件或新位置中,而这时力又会再次发生改变。例如,在狗和邮递员的问题中,邮递员一直保持运动状态,所以那条狗就必须时刻修正前进方向。
这正是微积分背后最令人赞叹不已的概念,试想一下,在即时的、每个无穷小的时间单位里正在发生什么。实际上,你正把一种无法言喻的思想变成一个强有力的预测工具。我们可以根据狗的行进路径在每个时刻的变化写出一个微分方程,表达“瞄准”的概念。通过解这个方程,我们知道了那条狗必须遵循的整个行进路线。整个轨迹是建立在狗追邮递员的无限小步子的基础上的。
这种把世界上任何事物都看成由无限小的变化累加而成的观点,是微积分最具革命性的见解。想出如何把这种思想变成可运算的数学方法是一个突破,这直接导致了17世纪微积分的创立。当时牛顿想通过计算推测出行星是如何运动的。他想到行星的运动是受不断变化的万有引力作用的,当它们绕太阳旋转时,它们与太阳的距离也在变化,这就改变了它们受到的引力。当行星在下一时刻移到一个新位置时,万有引力又会略有不同。计算出行星的运动轨迹就成了微分方程的一个问题。
通过解决追及问题,你会觉得自己正在与牛顿同行。这种感觉多好啊!
乔夫里先生给我们出的追及问题虽然很有挑战性,但还是可以解答的。这些追及问题的共性强化了我对数学公正性的感觉。我要做的就是把文字表达的问题转化成正确的方程式,耐心且准确地解代数问题,就一定可以得到正确的答案。
最先让我意识到我的浅薄的是我自己编的一道题。它很像那些我解过的追及问题,但由于某种原因,这道题变得特别难解,我花了好几个月的时间来解这道题。它既令我沮丧又让我极度渴望。我认为只要我付出足够的努力,肯定能攻克它,数个月的挫折会让征服的感觉变得更加美妙。
问题是这样的:
假设一条狗在一个圆形的池塘中间看见一只鸭子在围绕圆周游泳。狗为了追赶鸭子总是直接向它游去。换句话说,狗的速度向量总是与它和鸭子之间的连线有关。与此同时,鸭子以尽可能快的速度、按逆时针方向沿着池塘边游动以摆脱狗的追赶。假设这两种动物以相同的速度匀速游动,请列出狗游动路线的方程(见图2-3)。
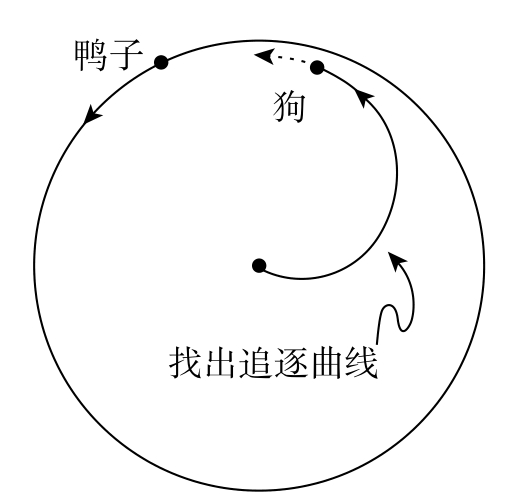
图2-3
狗渐渐接近鸭子所在的圆周的路径显然是螺旋式的。什么方程能表达螺旋线呢?
和绑在树上的山羊不同,山羊身上的线是越缠越紧的螺旋线,而这是一条扩展式螺旋线,从中心开始越来越大,但不会超过圆周的边界。
多么迷人的路径!
我算不出来。我试过了所有我能想出来的变量的变化,我还试图把这个问题简化成一个巧妙的微分方程。这个方程看起来应该是有解的,但我就是解不出来。
我当时不了解的是,有些数学问题是无解的,不可能获得明确的答案,正如我们的人生一样。
就像这个例子,没有公式可以表达狗追及的螺旋式路径,用我们常用的初等数学函数无法描述它,这个问题无解。
后来,我意识到这是一个法则,而不是一个例外。在这种情况下,大多数微分方程是无解的,我们的“公式图书馆”不足以解决它们。那些我们在高中学过的、能解的问题只是少数,因此弥足珍贵。