下载掌阅APP，畅读海量书库
立即打开
常用的主元分析（principal component analysis，PCA） [3] 通过线性变换输入变量的方法达到降维的目的。一些学者提出用线性逼近非线性的方法对PCA方法进行改进，如广义PCA [4] 、主曲线方法 [5] 、神经网络PCA方法 [6] 等，但这些方法对非线性问题的解决并不准确，且涉及复杂的算法变换问题。
在工程实际中，特征参数的变化往往呈现非线性，所以有必要采取非线性多元统计分析方法进行特征提取和分析。
基于核函数的主元分析方法（kernel PCA，KPCA）将输入数据映射到一个新的空间，这个过程是通过选定一个非线性函数实现的，然后在新空间中进行线性分析。该方法对于非线性数据特别有效，能提供更多的特征信息，并且提取的特征的识别效果更优 [7] 。核函数主元分析在机械设备状态和故障诊断应用中处于起步阶段。
主元分析是一种对数据进行分析的技术，最重要的应用是对原有数据进行简化，可以有效找出数据中最“主要”的元素和结构，去除噪声和冗余，将原有的复杂数据降维，揭示隐藏在复杂数据背后的简单结构。主元分析在原始数据空间基础上通过构造一组新的变量代替原变量，新变量的维数低于原始数据，新变量中包含原变量的特征信息，从而大大降低了投影空间的维数 [8-9] 。由于投影空间中特征向量相互垂直，变量之间的相关性被消除，独立性增强。
设 x =[ x 1 ， x 2 ，…， x p ] T 为一个 p 维总体，假设 x 的期望和协方差矩阵均存在并已知，记 E （ x ）= μ ，var（ x ）= Σ ，考虑如下线性变换 [10] ：
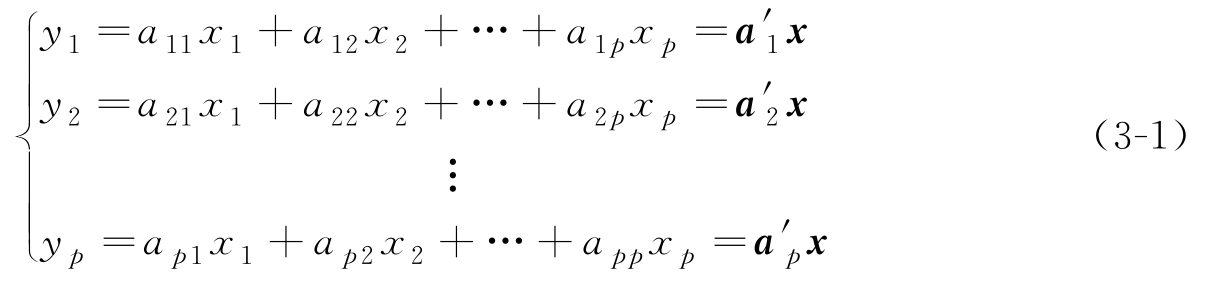
式中， a 1 ， a 2 ，…， a p 均为单位向量。下面求 a 1 ，使得 y 1 的方差达到最大。
设 λ 1 ， λ 2 ，…， λ p （ λ 1 ≥ λ 2 ≥…≥ λ p ≥0）为 Σ 的 p 个特征值， t 1 ， t 2 ，…， t p 为相应的正交单位特征向量，即
由矩阵知识可知
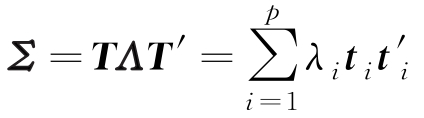
式中， T =[ t 1 ， t 2 ，…， t p ]为正交矩阵， Λ 是对角线元素为 λ 1 ， λ 2 ，…， λ p 的对角阵。考虑 y 1 的方差：
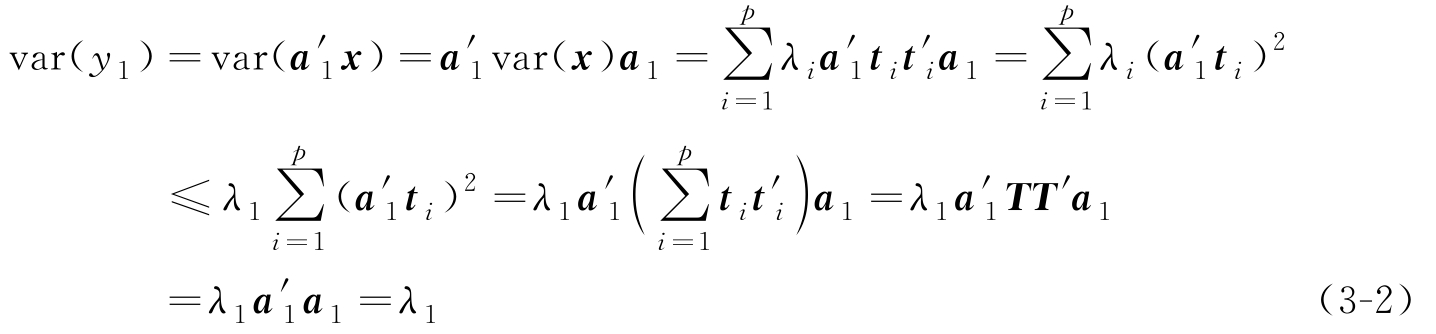
由式（3-2）可知，当
a
1
=
t
1
时，
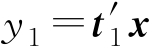的方差达到最大，最大值为
λ
1
。称
y
1
=
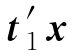为第一主成分。类似的，如果第一主成分从原始数据中提取的信息还不够，还应考虑第二、……、第
i
主成分。
总方差中第
i
个主成分
y
i
的方差所占的比例
（
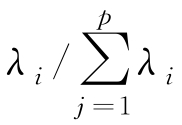i=
1，2，…，
p
）称为主成分
y
i
的贡献率。主成分的贡献率反映了主成分综合原始变量信息的能力或解释原始变量的能力。由贡献率的定义可知，
p
个主成分的贡献率依次递减。前
m
（
m
≤
p
）个主成分的贡献率之和
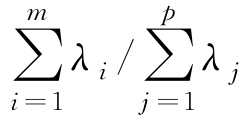称为前
m
个主成分的累积贡献率，它反映了前
m
个主成分综合原始变量信息的能力。由于主成分分析的主要目的是降维，所以需要在信息损失不太多的情况下，用少数几个主成分来代替原始变量
x
1
，
x
2
，…，
x
p
，以进行后续的分析。通常的做法是取较小的
m
，使得前
m
个主成分的累积贡献率不低于某一水平，这样就可以达到降维目的
[11]
。
基于核函数的主元分析方法（KPCA）的基本思想是 [12] 通过一个选定的映射 Φ 将输入样本 x 变换到其他空间，成为 Φ （ x ），然后对 Φ （ x ）利用PCA线性特征提取方法进行计算，将非线性问题变换为线性问题，可用图3-1描述其过程。
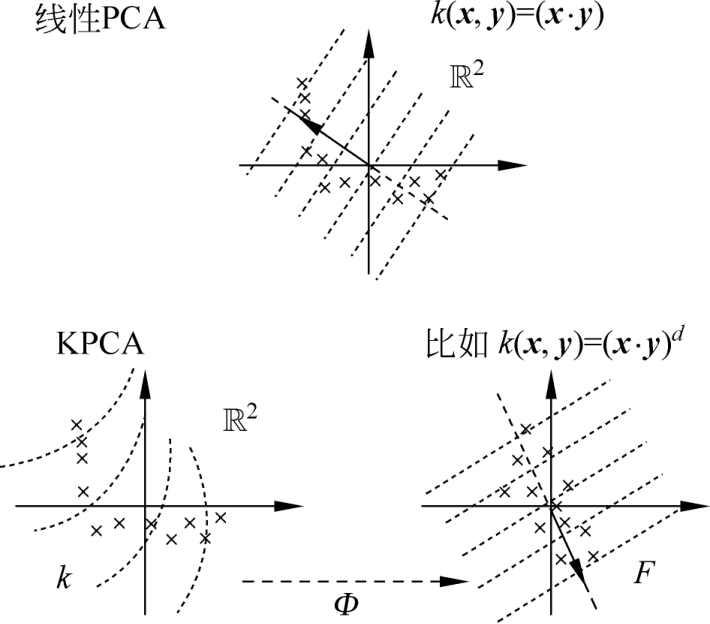
图3-1 PCA/KPCA空间转换示意图
假设 x 1 ， x 2 ，…， x N 为训练样本，用{ x i }表示输入空间。选择的变换函数为 Φ ，变换到特征空间需要满足的条件为
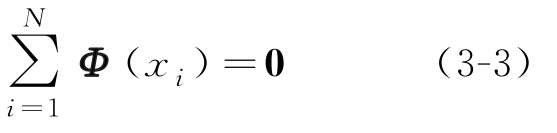
求其协方差矩阵为
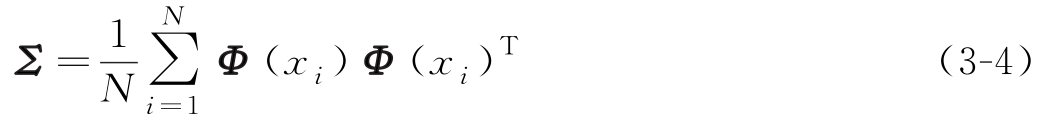
若不满足式（3-3）的条件，其操作步骤详见文献[13]，可认为 u i 位于 Φ （ x 1 ）， Φ （ x 2 ），…， Φ （ x N ）张成的子空间中，即
式中，
。
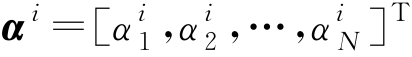事实上，式（3-5）对应特征空间中的目标函数可表达为如下拉格朗日函数：
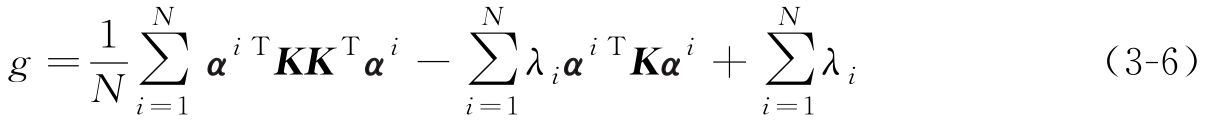
式中，（ K ） ij = k （ x i ， x j ）= Φ T （ x i ） Φ （ x j ）， g 取极值时，需满足
令 λ' = Nλ i ，则式（3-7）等价于如下特征方程：
PCA与KPCA方法的区别在于：在PCA分析中，新的特征是原始特征的线性组合，代表点到直线的最小距离；在KPCA分析中，是通过选定的变换函数将原特征映射到新的空间形成新特征，代表点到曲面的最小距离。
由于映射的非线性，因此KPCA是一种非线性主元分析方法。如果原始数据存在复杂的非线性关系，相比主元分析而言，非线性主元分析更适合用作对其进行特征抽取。KPCA即是一种非常成功的非线性主元分析方法。
根据式（3-8）计算训练样本集{ Φ （ x i ）}的特征值为 λ 1 ， λ 2 ，…， λ m （ m ≤ N ），相应的特征向量为 α 1 ， α 2 ，…， α m ，并假设特征空间中单位变换轴为 u 1 ， u 2 ，…， u m ，则
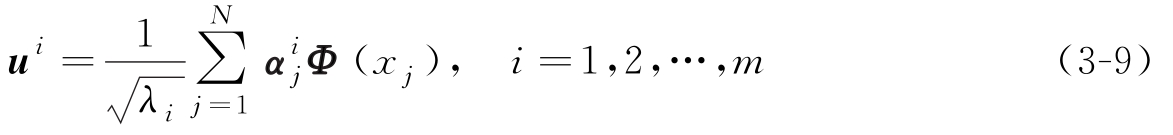
变换轴 u i （ i =1，2，…， m ）的单位性（（ u i ） T u i =1）， u i 与 u j 的正交性显而易见。基于式（3-9），可以计算出特征空间中样本 Φ （ x ）在 u i 上投影的计算式，样本 x 在特征空间中的特征抽取结果为
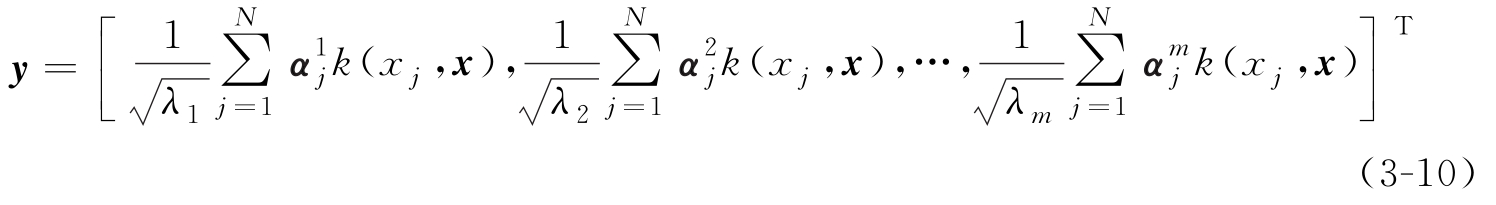
在应用中，根据实际情况选定 m 值，根据式（3-10）给出的特征提取结果进行故障分类。
应用KPCA进行特征提取时，对系统的计算能力要求很高，这是因为需计算样本间的核函数，并加权求和，如果样本较多，系统的效率就会下降 [14] 。若能对KPCA方法的效率进行提升，将对实际应用非常重要 [15] 。
在用训练样本表示式（3-9）中的 u i 时，不同样本的贡献率不一样，某些样本占较大权重，而另一些则相反。计算权重较小的样本耗费了计算时间，但对计算结果影响不大，若能从整体样本中找出对逼近最优变换轴影响大的那部分样本，则可减少KPCA特征提取的计算量。
因此，降低计算量的关键是确定找出重要样本的依据，根据特征方程特征值的大小判断训练样本在逼近最优变换轴方面的贡献率大小是可行的方案。特征值越大，相应最优变换轴对原数据的逼近程度就越强，采用该数据进行故障分类时包含原数据的信息越多。
假设
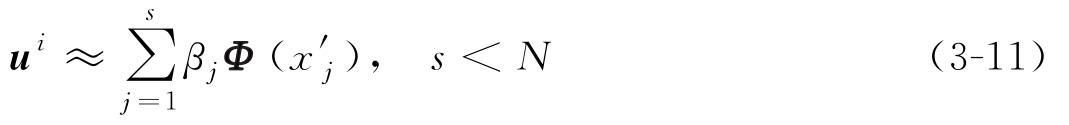
式中，
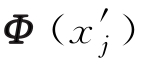来自训练样本集，称为特征空间中的节点。
令
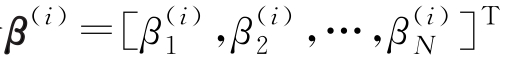，则式（3-6）变形为
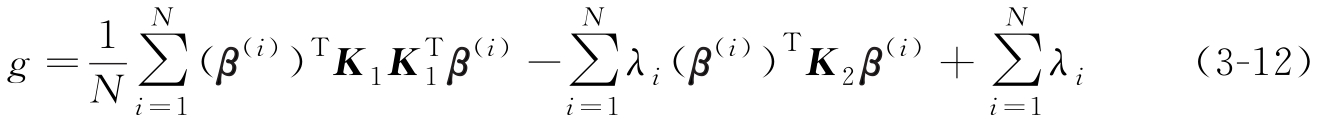
式中
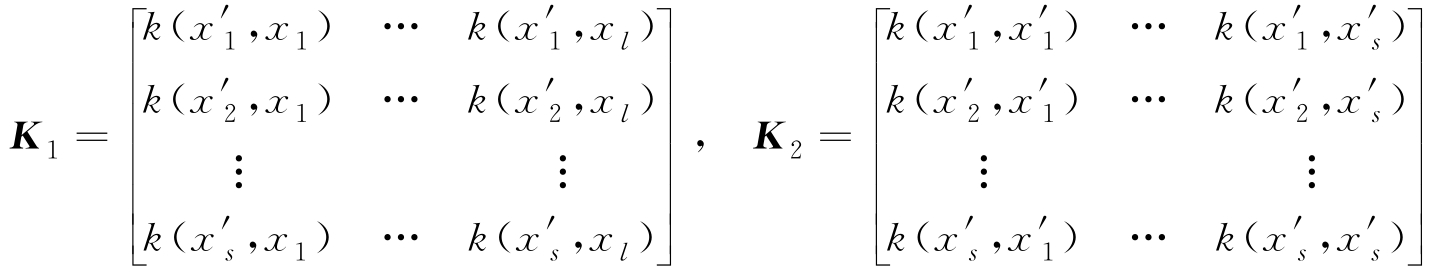
将式（3-12）对 β （ i ） 求导，可得如下广义特征方程：
在
K
2
可逆条件下，令
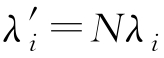，该特征方程可改写为
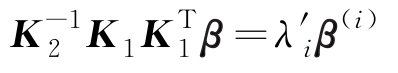
将 Φ （ x ）在这 m 个最优变换轴上的投影值组成向量，则特征空间中样本 Φ （ x ）基于改进的KPCA方法的特征抽取结果为
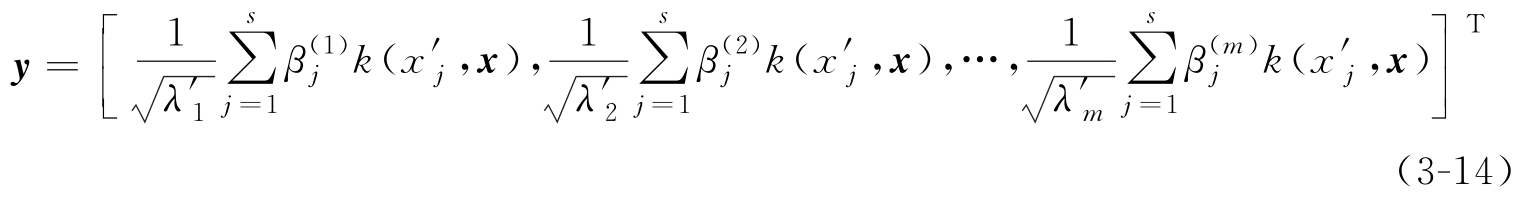
式中，
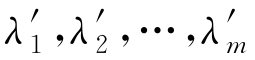为式（3-13）的前
m
个最大特征值；
β
（1）
，
β
（2）
，…，
β
（
m
）
为分别对应这
m
个特征值的特征向量，
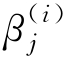为向量
β
（
i
）
的第
j
维分量。