




上文中我们只谈到了直线运动,对自然界中其他可以观察到的种种运动还知之甚少。我们还必须观察曲线运动,下一步还要确定这些运动遵循的定律。这绝非易事。在上述我们谈到的直线运动中,速度、速度的改变、力等概念对我们帮助很大,但是我们很难立刻弄清楚应该如何把这些概念应用到曲线运动中。我们甚至有理由认为新概念需要被创造出来,因为旧概念已经不足以描述广泛的运动。那么我们是该沿着旧路走,还是另辟蹊径呢?
对概念进行归纳推广是科学研究中常用的办法。进行归纳推广并不是唯一的方法,实际上,很多方式都能做到。但是无论采取何种方式,我们都必须严格地遵照一个要求:归纳推广的前提条件充足时,推广后的概念必须能够简化为原始概念。
我们现在正在讨论的例子就能很好地解释这一点。我们可以尝试归纳速度、速度的改变和力等概念,然后将它们推广至曲线运动。从严格意义上说,曲线是包含直线在内的,直线只是一种特殊的曲线,占比很小。因此,如果速度、速度的改变和力能够用于曲线运动,那么它们可以很自然地用于直线运动,但是其结果绝对不能跟我们之前得到的结果相矛盾。如果曲线变成直线,那么所有在曲线运动中归纳推广后的概念都必须被还原为直线运动中我们已经熟知的概念。但是仅仅这样一个限制条件还不足以决定归纳推广的过程,因为如果只有这一个限制条件的话,其他多种可能性就可能被忽略。透过科学史我们可以看到,最简单的归纳推广有时成功,有时失败。首先,我们要做一个猜测。在目前我们讨论的这个例子里,猜出正确的归纳推广方法并不难。归纳推广后的新概念是非常成功的,它既能帮助我们理解向空中抛掷石子的运动,又可以帮助我们理解行星的运动。
速度、速度的改变和力这几个概念在曲线运动中一般表示什么意思呢?我们先来看一看速度。如图1-8所示,一个很小的物体沿着曲线从左向右运动,我们通常把这样的小物体称作质点。如果曲线上的黑点表示这个质点在某一瞬间的位置,那么,速度在此时此地是怎样的呢?和之前一样,伽利略提供的线索可以帮助我们理解这里的速度。请再设想一个理想化的实验:质点在外力的作用下,沿着曲线从左向右运动,如图1-9中的黑点所示,在某个给定的时刻或位置,所有的外力突然停止作用。那么,根据惯性定律,运动应当是匀速直线的。在实际情况中,我们当然不可能使物体完全不受外力的影响。我们只能推测:“假设……,结果会怎样?”而后我们再根据推测所得出的结论以及其与实验结果是否相符来判断我们的推测是否合理。

图1-8

图1-9
图1-10中的矢量表示假设所有外力消失时我们所猜测的质点匀速运动的方向,即所谓的切线方向。透过显微镜来观察某一时刻质点的运动轨迹,我们只能看到极小一部分曲线,它显现为很短的线段,切线就是它的延长线。因此,图上画出来的矢量就代表运动的质点在该给定时刻的瞬时速度,速度矢量就在切线上,它的长度代表速率,就像汽车速度计上所显示的数值一样。
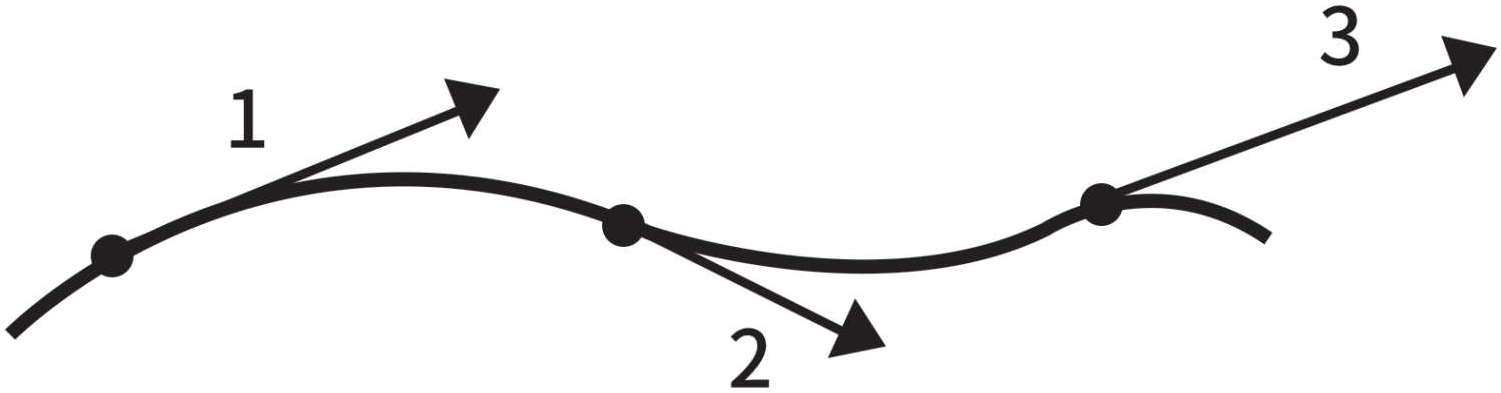
图1-10
对于破坏运动,寻求速度矢量的这个理想化实验,我们不必较真。它只能帮我们搞懂速度矢量的名称,方便我们确定在某个特定时间和特定位置的速度矢量。
图1-10显示了同一个质点在沿一条曲线运动时在3个不同位置上的速度矢量。在该图中,我们可以看到质点运动的方向和速度的数值(表现为矢量的长度),在运动过程中都在不断变化。
这个新的速度概念能否满足归纳推广过程中的所有需求呢?换句话说,如果曲线简化为直线,它是否也能够简化为以前的速度概念呢?显然是可以的。当运动轨迹是直线时,其切线就是直线本身,速度矢量的方向与运动方向重合,这种情况跟做直线运动的小车或者滚动的小球是一样的。
接下来我们就要谈到沿着曲线运动的质点的速度变化。这里有多种方法,我们会从中选择最简单便捷的。图1-10中的几个速度矢量分别代表曲线上不同位置的运动。我们可以再画一下前面的两个矢量,让它们从同一点出发。我们已经知道,对矢量而言,这样做是可行的(图1-11)。我们把虚线矢量称为“速度的改变”。虚线矢量的起点是第一个矢量的终点,而终点是第二个矢量的终点。乍一看,“速度的改变”这个定义似乎有些牵强且没有意义。在下述特殊情况中,也就是矢量1和矢量2的方向相同时,这个定义就变得更加清晰易懂了。当然,这又回到直线运动上去了:如果两个矢量起点相同,那么虚线矢量依旧是把它们的终点连接起来,如果画出来的话,就跟图1-6或图1-7完全相同,而以前的概念就成为新概念的一种特殊情况。在图中,我们需要把两根线分开,因为如果不这样的话,它们就会重合,难以分辨了。
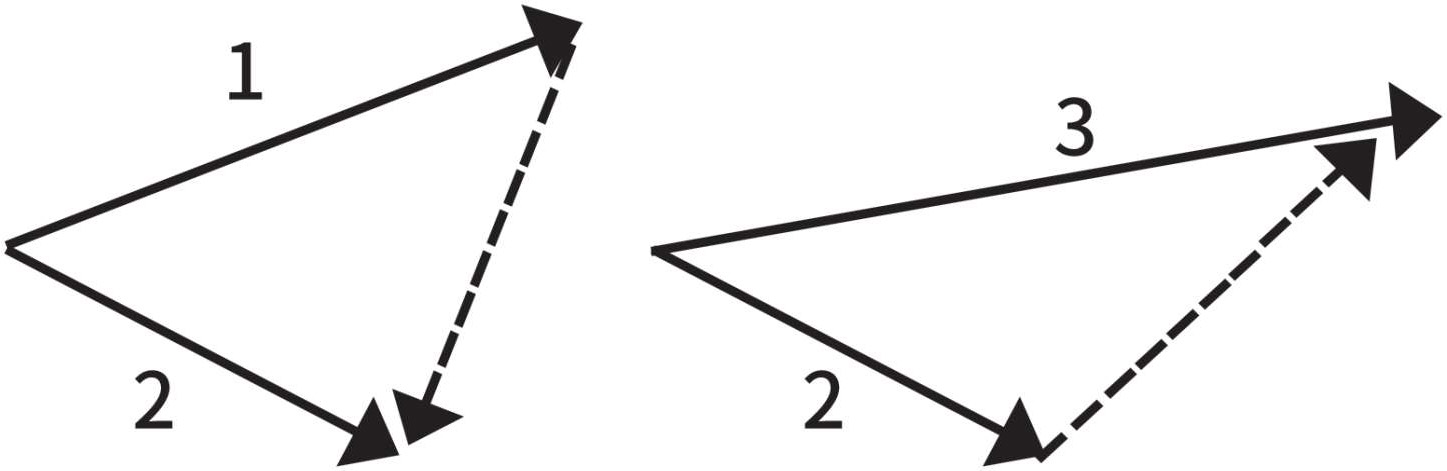
图1-11
现在我们来进行归纳推广的最后一步。这是迄今为止我们做过的诸多猜想中最为重要的一个。我们必须要在力与速度的改变之间建立起联系。只有这样,我们才能够找到理解关于运动的普遍问题的线索。
理解直线运动的线索是非常简单的:外力导致了速度的改变,外力的矢量方向跟速度改变的方向是相同的。那么,现在什么是可以帮助我们理解曲线运动的线索呢?还是速度!唯一的区别在于现在速度改变的意义比以前更宽泛了。只要看一下图1-11和图1-6中的虚线矢量,我们就能清楚地认识到这一点。只要知道曲线上任意一点的速度,我们就能推导出任意一点上力的方向。我们必须取曲线上时间间隔相距极短的两个点,相应地,这两个点的位置也极相近。连接第一个矢量的终点和第二个矢量的终点的这个矢量的方向,就是作用力的方向。但是必须要记住,两个速度矢量的时间间隔必须是“极短”。要想严格地定义“极短”和“极近”这样的概念是非常困难的。事实上,为了能够准确分析这样的概念,牛顿和莱布尼兹(Leibnitz)发明了微积分。
我们煞费苦心,花了很长时间才对伽利略提供的线索进行了归纳推广。我们无法写尽归纳推广后的线索为人类带来了多少丰厚的回报。总之,对其归纳推广及应用后,许多之前看起来互不相关的和难以理解的事情都能够以最简单的方式加以解释,并且让人信服。
我们应该从现实中存在的各种各样的运动中选取最简单的,用刚才所谈到的定律来进行解释。
枪射出来的子弹,斜抛而出的石子,水管里喷射出来的水,这些物体的运动路径都是大家非常熟悉的抛物线。假设我们在石子上绑上一个速度计,那么我们就可以画出石子在任何时刻的速度矢量。其结果在图1-12中可以被充分体现出来。作用在石子上的力的方向就是速度改变的方向,我们已经知道这个方向是如何判断出来的。图1-13中指出,作用在石子上的力是垂直向下的,这跟我们在塔顶向下扔石子的情况完全一样。二者的运动路线和速度完全不同,但是速度改变的方向是相同的,即朝向地球的中心。
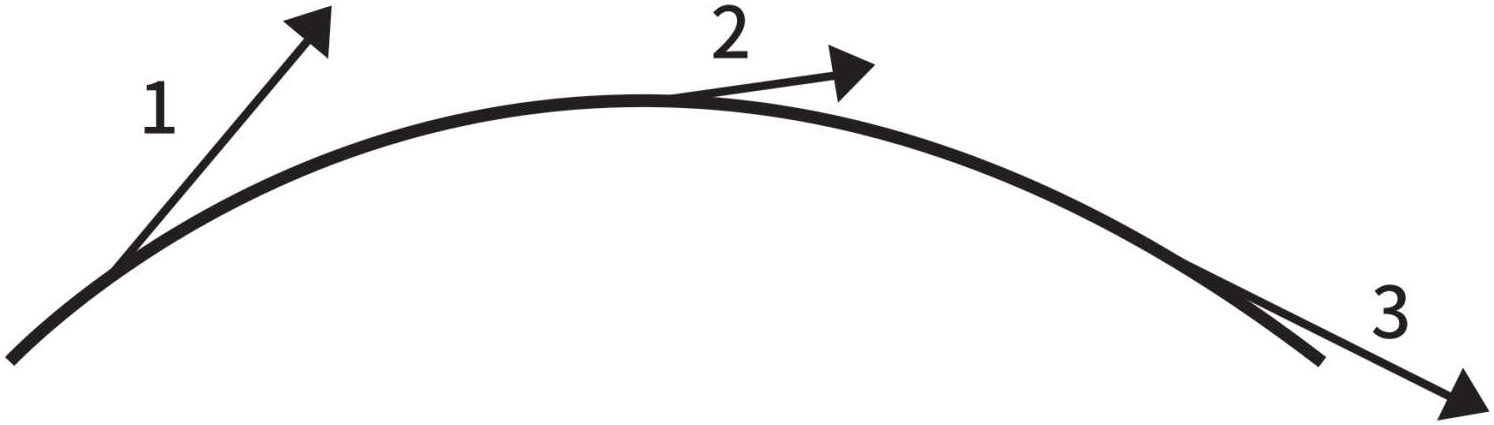
图1-12
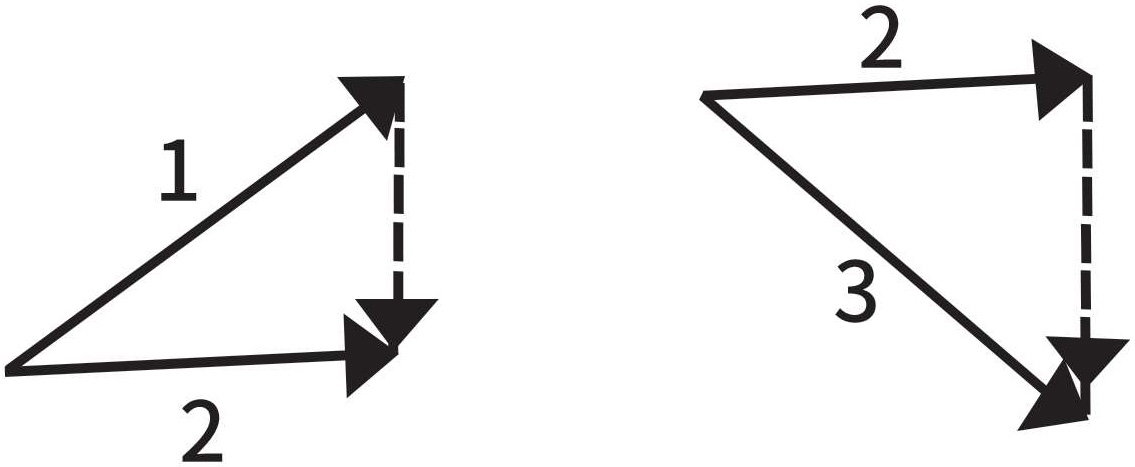
图1-13
把石子绑在一根绳子的末端,并在水平面上挥动绳子,石子就会做圆周运动。
如果运动是匀速的,那么图中表示速度的所有矢量长度都相等。然而速度矢量并不都一样,因为运动的路径并非直线。只有在做匀速直线运动时,物体才不受任何外力的作用。在外力作用下,速度的大小是一样的,方向却在不停地改变(图1-14)。根据运动定律,肯定是外力导致了这种变化。在这个例子中,方向改变是因为在石子和握绳子的手指间存在一个力。于是我们马上就发现了一个新问题:力起作用的方向是什么呢?我们同样用一个矢量图来回答这个问题。如图1-14、图1-15所示,请找到运动路径上相距极近的两点,并画出其速度矢量,这样我们就可以看出速度的改变。不难看出,这个矢量以运动路径的圆心为中心,沿着绳子做运动,且永远与速度矢量或圆的切线垂直。换句话说,手通过绳子对石子施加了一个力。
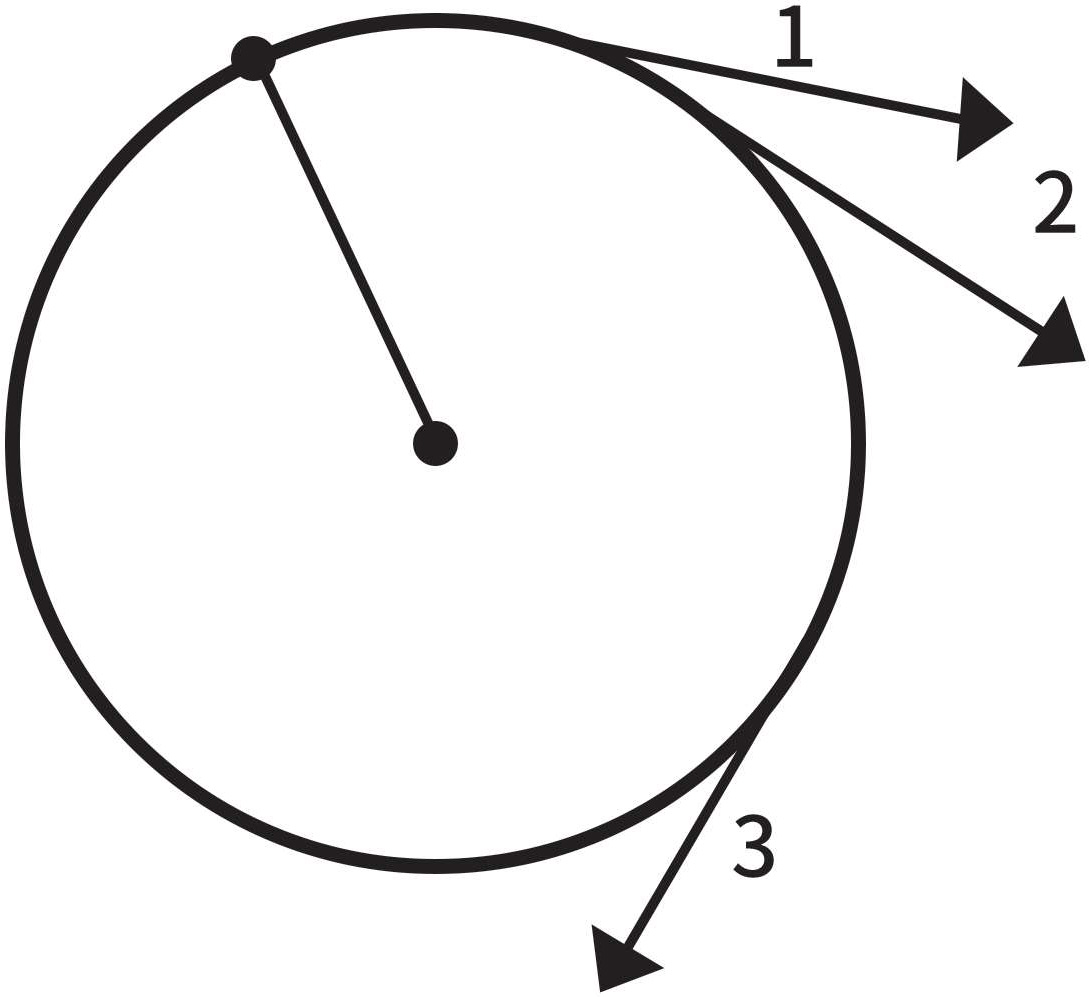
图1-14
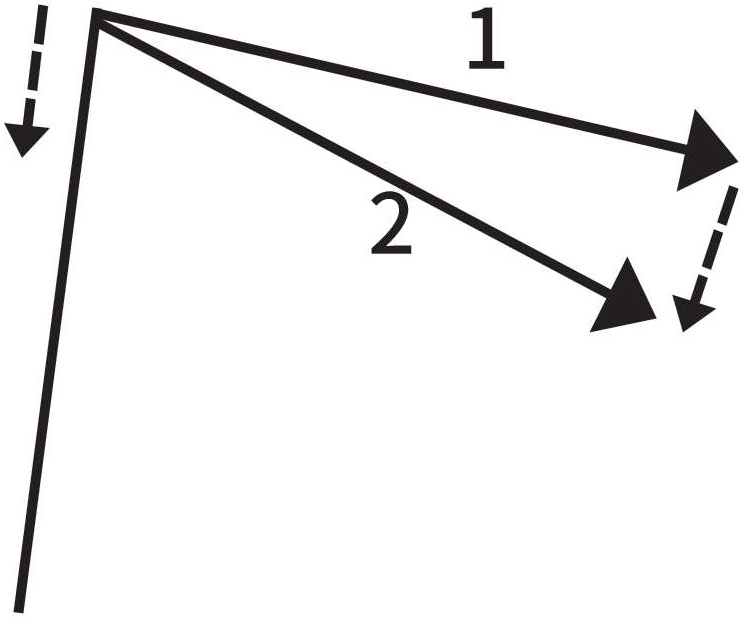
图1-15
与这个例子相似但更有价值的案例是月球围绕地球的转动。其大体可以看作匀速圆周运动。作用在月球上的力的方向是朝向地球的,这和刚刚谈到的石子所受力的方向朝向手原因相同。当然,地球与月球之间不存在什么绳子把两者连在一起,但是我们可以设想一下:在月球和地球的中心之间有一条线,力沿着线的方向,朝向地球的中心,就和石子被抛向空中或从塔上被扔下时所受的力一样。
前面我们谈到的所有关于运动的内容都可以用一句话来总括:力与速度的改变是方向相同的矢量。这是我们解决运动问题的最初线索,但要想完美地解释我们观测到的所有运动,显然还不够。从亚里士多德到伽利略,人类思维方式的转变,已成为科学基础形成中极为重要的基石。这种转变出现之后,科学发展的路线就很清晰了。这里我们重点关注的是发展的最初阶段。在我们同旧概念的艰苦斗争中,是如何找到最初的线索的?新的物理概念又是如何诞生的?我们只关注科学的开创性工作,集中寻找新的、未预见的科学发展新道路。随着科学思维的不断发展,我们对于这个世界的认识在不断变化。最初和基本的探索总是革命性的,科学的思维会看到旧概念的局限性,于是用新的概念取而代之。沿着任何一条已知的路继续发展,究其本质,都是进化,而非革命,除非我们能够到达下一个转折点,也就是征服新的领域。但是为了弄清楚究竟是哪些原因和困难迫使我们改变一些重要的概念,我们不仅要知道最初的线索,还要知道由这些线索推导出的结论。
现代物理学最重要的一个特征是:由最初的线索推导出来的结论,不仅是定性的,而且是定量的。让我们再想一下从塔上扔下石子的例子。我们已经知道,随着石子逐渐下落,它的速度会逐渐增加。但是我们还应该知道更多,比如:速度改变了多少呢?在开始掉落以后的任何一个瞬间,石子的位置和速度是怎样的?我们希望能够预测事件结果,并用实验来验证观察结果与最初的假设是否相符。
我们要想得出定量的结论,就得用数学语言。大多数基本的科学理念,究其本质都是比较简单的。因此,一般而言,它们可以用浅显易懂的语言来表达。但要理解这些理念,需要极强的推理能力。如果我们想得出和实验效果相当的结论,那么数学可以成为一个必要的推理工具。本书只讨论基本的物理学观念,所以我们不使用数学语言。为保持在本书中一直不使用数学语言,我们要避免引用一些必要的结果(无证据),即使它们在进一步发展过程中产生了重要线索。放弃数学语言必须要付出一些代价,那就是丧失一定的精确性,而且有时候我们会引用一些结果,却不会说明它们是如何得出的。
关于运动的一个非常重要的例子是地球绕太阳的运动。大家都已经知道,其运动路线是一个椭圆形的闭合曲线(图1-16)。通过画出速度改变的矢量图,我们可以看到作用在地球上的力是指向太阳的。但是这点信息还远远不够。我们希望预测地球及其他太阳系行星在任何时刻的位置,下一次日食以及许多其他天文现象的日期和持续时间。做到这些事情是有可能的,但只依靠最初的线索是不够的,因为我们不仅仅必须知道力的方向,还要知道它的绝对值,也就是力的大小。牛顿受到启发,在这方面做了一个猜想。根据他的引力定律,两个物体之间的引力与它们的距离存在一种很简单的关系:距离增加,引力减小。说得确切些,当距离增加到原来的2倍,引力就会变为原来的1/4;当距离增加到原来的3倍,引力便减小到原来的1/9。
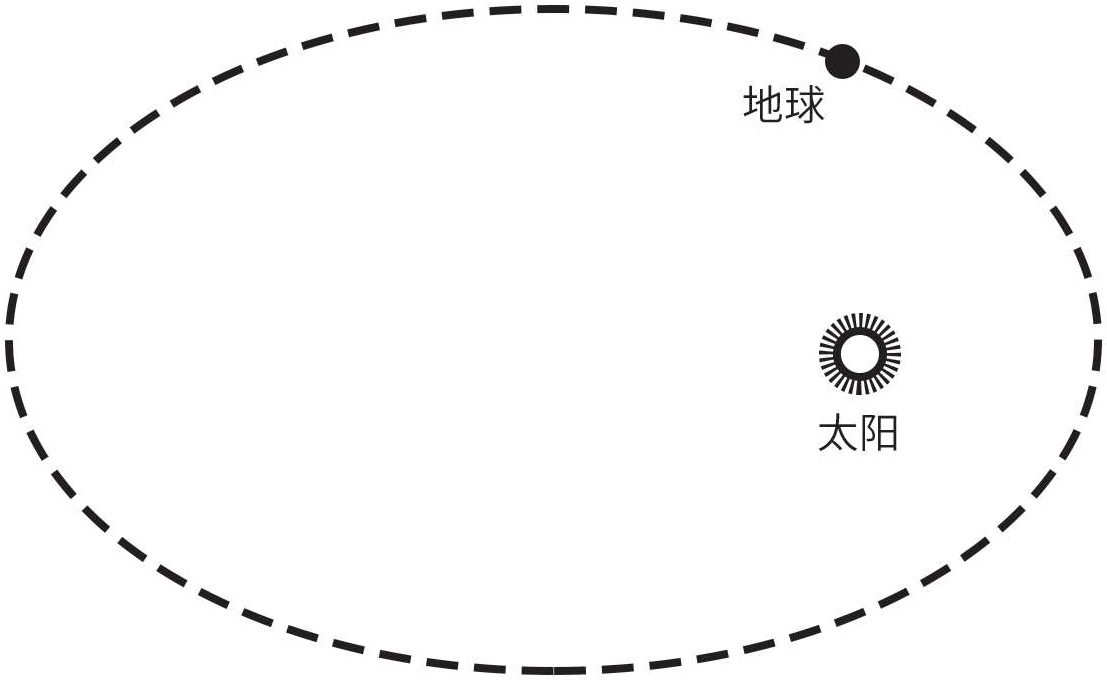
图1-16
因此,我们可以看到,在万有引力方面,我们能以很简单的方式把两个运动物体之间的引力与距离的关系表示出来。我们还可以用相同的方式应对所有其他情景下出现的各种不同的力,如电力、磁力等。我们试图用一种简单的方式来解释力,而这样的表述是否正确,要看由它推导出来的结论是否与实验结果相符。
但是仅具有引力方面的知识并不足以描述行星的运动。我们已经知道,在极短时间间隔内的力和速度改变的矢量,它们的方向是相同的。但如果我们跟着牛顿进一步研究,假设它们的长度之间存在着一种简单的关系,如果所给定的其他所有条件都相同,也就是说,研究同一个运动的物体在相同的时间间隔内速度的改变,按照牛顿的说法,所得结果应是速度的改变与作用力的大小成比例关系。
为了得出关于行星运动的定量结论,我们需要补充两个猜想。一个是一般意义上的,可用于说明力和速度改变之间的关系;另一个则是特殊的,可用于说明这种作用在物体上的特殊的力和物体之间距离的关系。第一个是牛顿关于运动的普遍定律,第二个是他的引力定律。将这些定律结合起来就是运动遵循的定律。下面一个似乎很简单的推理就能把运动定律解释清楚。假设我们能够确定在某特定时刻行星的位置和速度,并且也知道力,那么,根据牛顿定律,我们便能够知道在极短时间间隔内的速度改变。知道了初速度和速度的改变,我们就可以知道在这个时间间隔结束时行星的速度和位置。通过不断重复这个过程,我们不用观察数据就可以得到整个运动路线。从原则上来说,这是力学用以预测物体运动路线的方法,但在这里并不适用。实际上,这种渐进的步骤异常烦琐且极不准确。幸运的是,我们完全没有必要使用这种方法。数学给我们提供了捷径,使我们能够十分准确地描述运动,而且这种描述比我们平时说的一个句子还要简洁。用这种方法所得到的结论可以通过观察来证明或推翻。
同样的外力还出现在石子从空中落下的运动以及月球按轨道绕地球转动的运动中,这体现出了地球对物体的引力。牛顿认为:石子落下的运动、月球绕地球转动其实都是两个物体之间存在万有引力的特殊表现。在简单的情况下,我们可以运用数学手段去描述和预测运动;在非常复杂的情况下,当两个物体相距极远时,会牵扯到很多物体彼此之间的作用,用数学手段去描述就会难得多,但基本的原理都一样。
沿着最初的线索,通过分析石子从空中落下的运动以及月亮、地球和其他行星的运动,我们最终得出了结论。
通过实验来证明或者推翻的是我们的所有猜想。我们不能从之前的假设中单独拿出来一个进行测试。在行星围绕太阳运动的例子中,应用力学体系能够很完美地对其进行解释。然而,我们也不难想到,基于不同猜想的另一套体系也许同样能够完全解释这些。
虽然看起来如此,但是物理学概念并不是由外部世界决定的,而是由人类思维自由创造出来的。我们一直在尝试理解现实,这有点像一个人想弄清楚一个表盖关闭的钟表的原理。他能够看到走动着的指针,甚至可以听到滴答声,但是他无法打开表盖。如果能进行创造性思考,他大概能理出来一些原理以解释观察到的一切现象。但是,他永远不能完全断定,他自己理出来的原理就是他所观察到的现象的唯一解释。他永远不能把自己设想出来的原理跟实实在在存在的原理进行比较,甚至不能想象这种比较到底存不存在可能性或者到底有没有意义。但是他完全相信:随着他的知识不断增加,他用于描述现实的原理也会越来越简单,并且它能逐渐解释越来越多的他观察到的现象。他也相信,在理想状态下,知识存在极限,而人类的思维正在逐步接近这个极限。他可以把这个理想状态下的极限叫作客观真理。