质量弹簧阻尼系统中对于不同的输入方式有两种形式,一种如图 3.3.1 所示的外部激励力 f ( t )直接作用在质量 m 上,根据力平衡条件其强迫振动方程可表示为
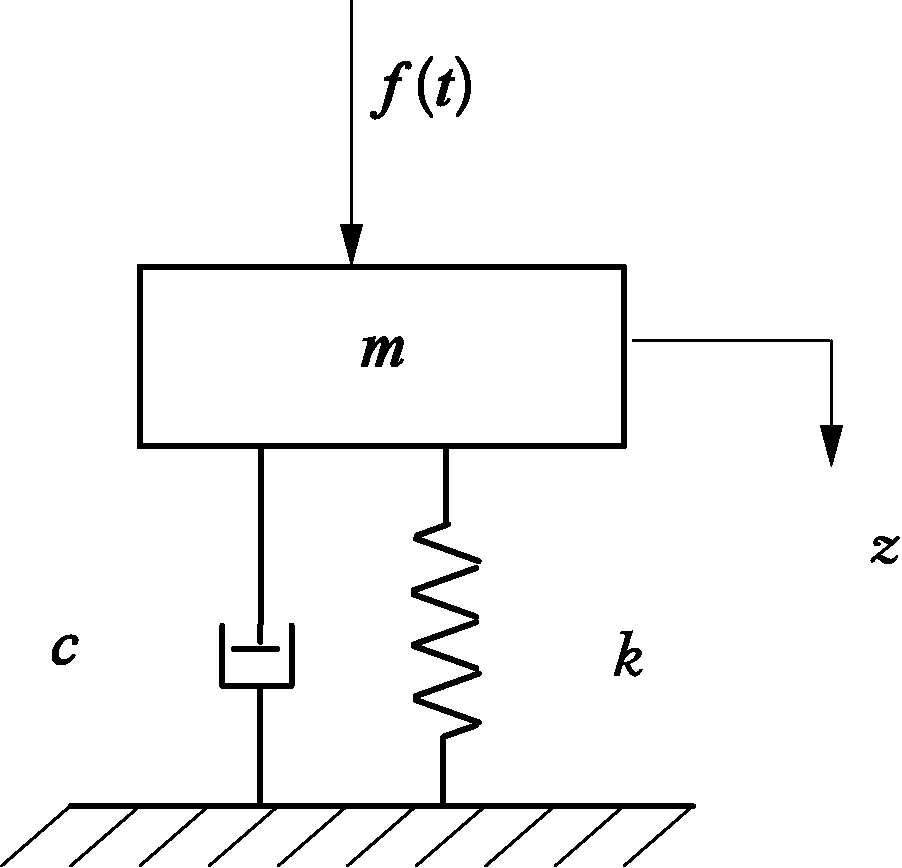
图3.3.1 单自由度振动系统激励力输入
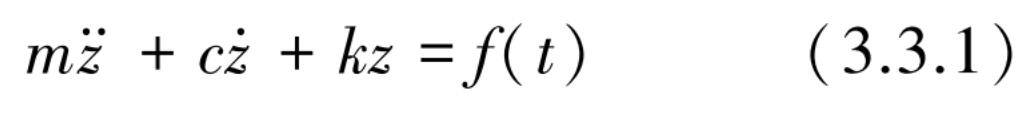
也可表示为
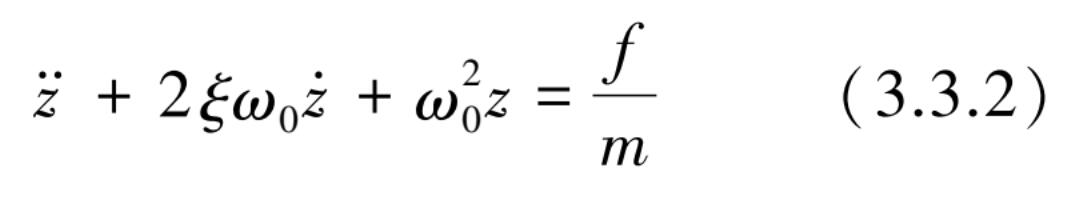
式中,
 =
=
 ,为无阻尼下固有圆频率;
ξ
=
,为无阻尼下固有圆频率;
ξ
=
 =
=
 ,为阻尼比;
,为阻尼比;
 =
=
 =
=
 ,为临界阻尼系数。
,为临界阻尼系数。
另外一种如图 3.3.2 所示的外部位移 x ( t )作用在系统的基础上,其强迫振动方程可表示为
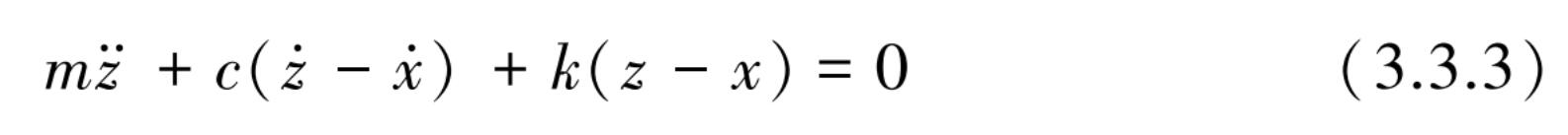
设相对于基础的位移为

代入式(3.3.3)后用相对位移 y 表示的振动方程为
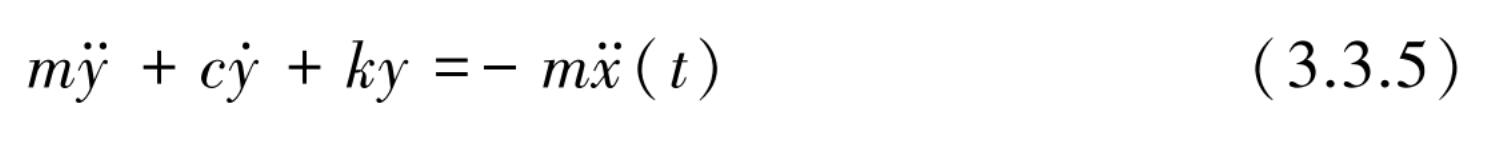
也可表示为
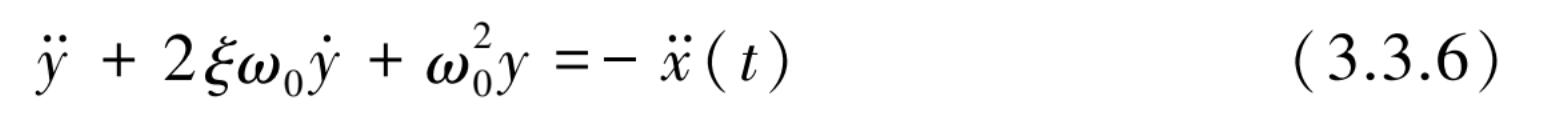
绝对加速度
 由式(3.3.3)直接得到
由式(3.3.3)直接得到
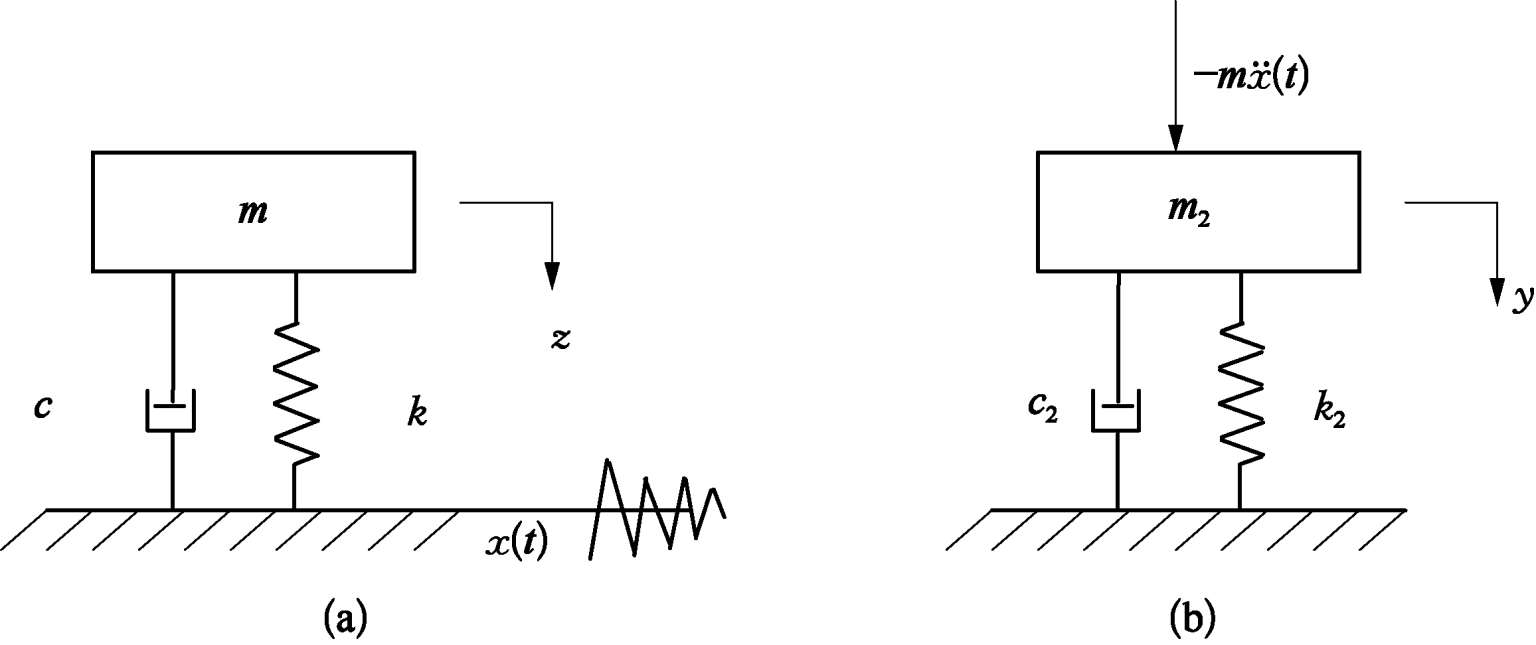
图3.3.2 单自由度振动系统基础位移输入
(a)原系统;(b)等效系统

对于式(3.3.5)与式(3.3.1)在振动方程的表达形式上完全相一致,其等效振动系统相当于图 3.3.2(b)所示,其中等效对应的参数为

一般设施的抗震分析中常以地面(或楼面)的基础输入为主,所以本书讨论的强迫振动均以式(3.3.6)和式(3.3.7)作为基本振动方程进行求解。另外抗震分析常常采用地震反应谱分析方法。
首先从式(3.3.6)作为相对位移 y ( t )入手,求解 y ( t )时可设为其解分为通解 y 1 和特解 y 2 的线性叠加。

通解 y 1 从齐次方程中求得,即
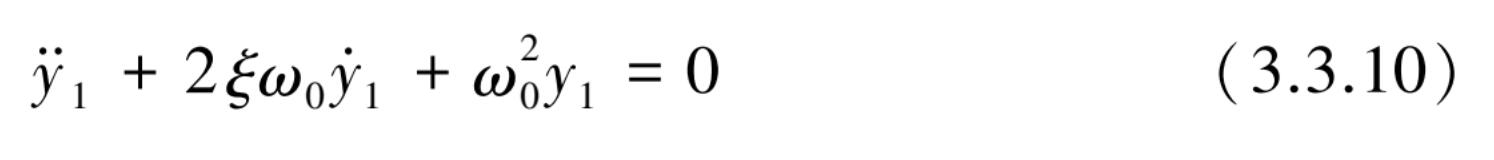
其通解可参照 3.2.4 节中自由振动的解得到
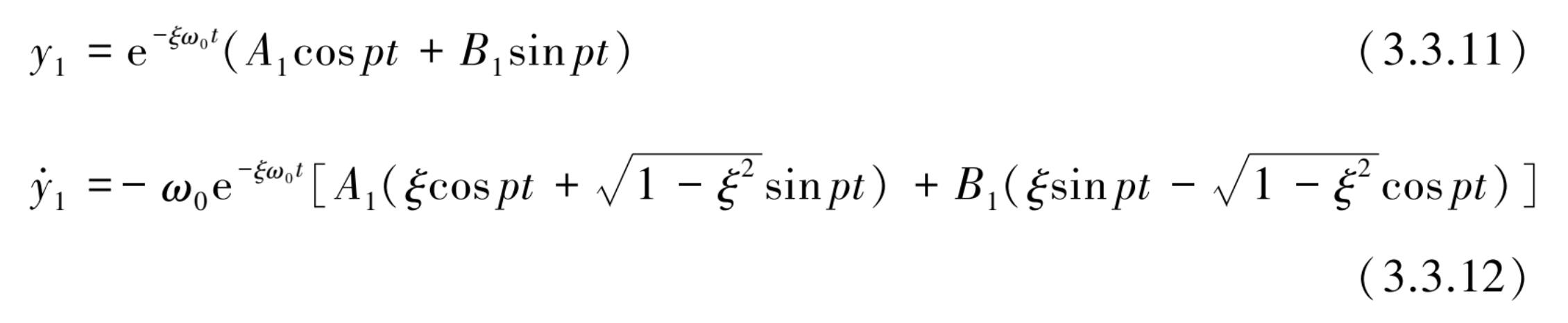
式中,
p
=
 为系统固有圆频率;
A
1
和
B
1
为积分常数,可根据总位移
y
在初始时间
t
=0 时的位移
y
0
和速度
为系统固有圆频率;
A
1
和
B
1
为积分常数,可根据总位移
y
在初始时间
t
=0 时的位移
y
0
和速度
 求得。
求得。
对于式(3.3.6)的特解 y 2 ,可以采用通解 y 1 中的常数变量方法求解,即将通解 y 1 中积分常数 A 1 和 B 1 假设为是时间 t 的函数,即方程通解(3.3.11)可改为
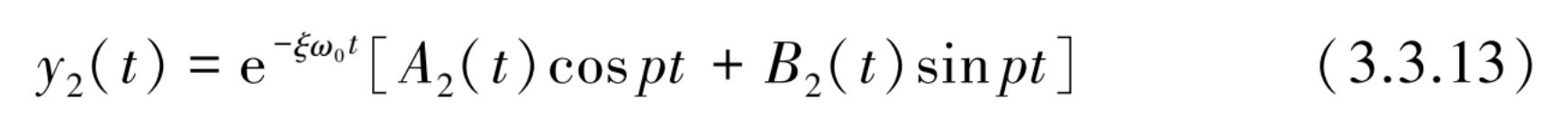
y 2 ( t )对 t 求导得
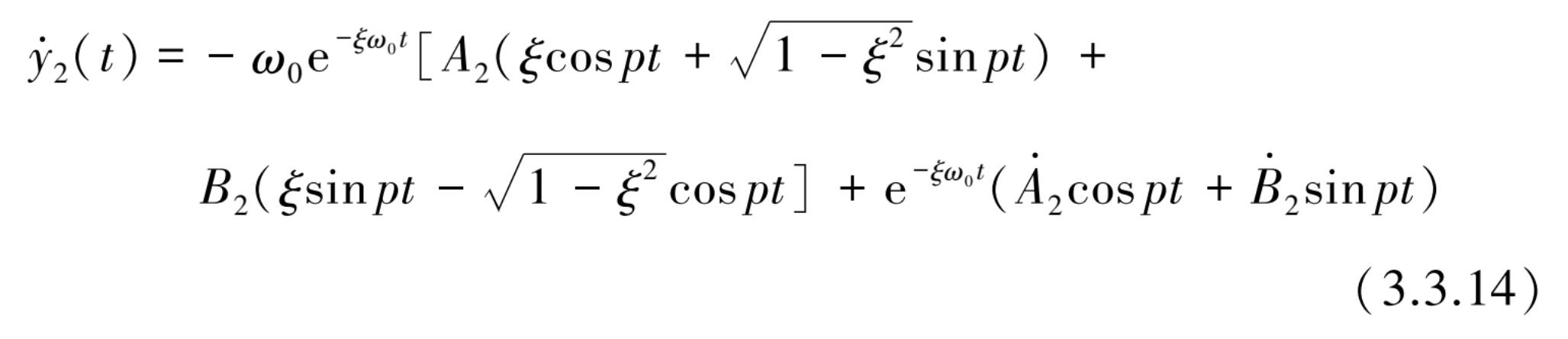
令
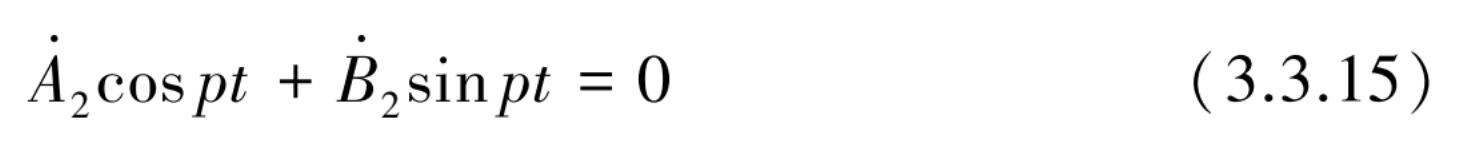
则
 表达式与式(3.3.12)形式上完全相同,可表示为
表达式与式(3.3.12)形式上完全相同,可表示为
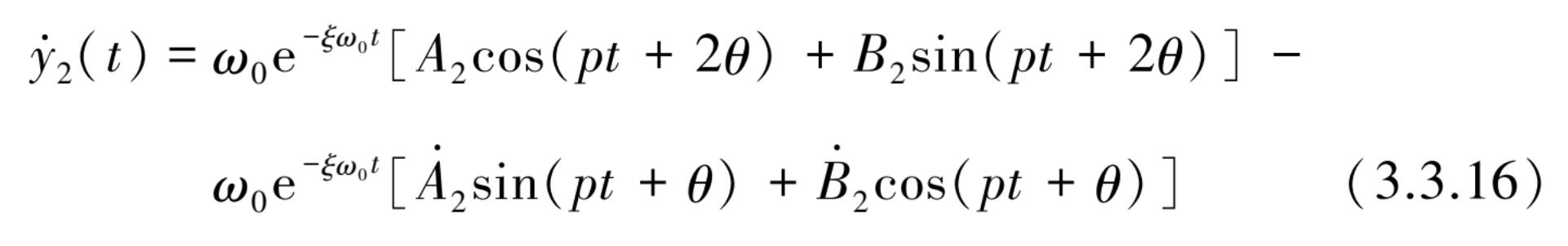
同理对
 求寻可得到
求寻可得到
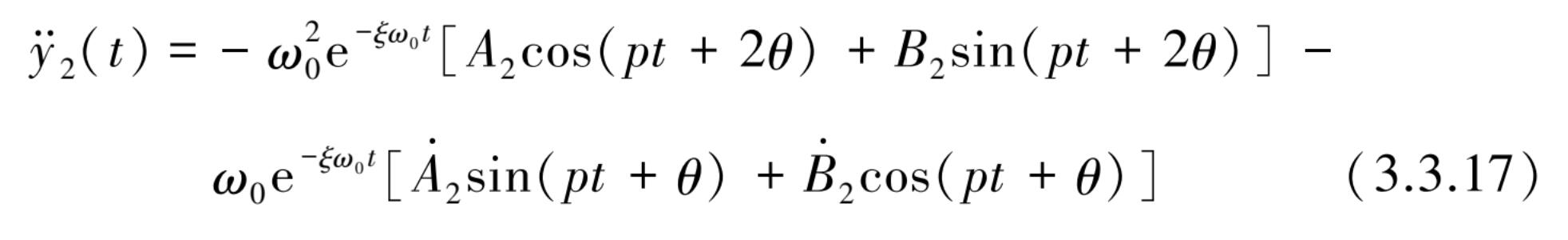
式中,
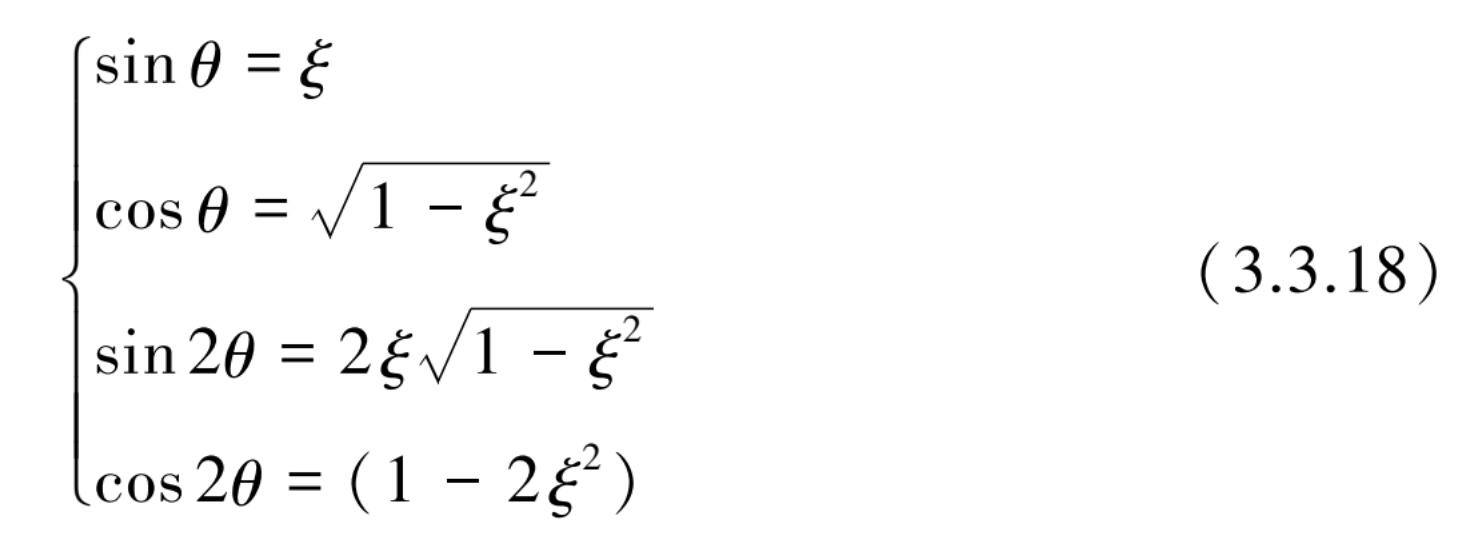
将式(3.3.13)、式(3.3.16)和式(3.3.17)代入振动方程式(3.3.6)后,考虑到 A 2 和 B 2 满足齐次方程解的条件,经整理后得
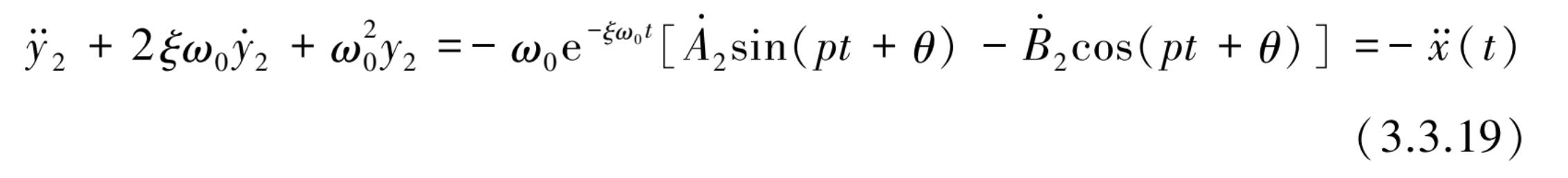
由式(3.3.15)与式(3.3.19)可得到
 和
和
 二元一次代数方程式。
二元一次代数方程式。
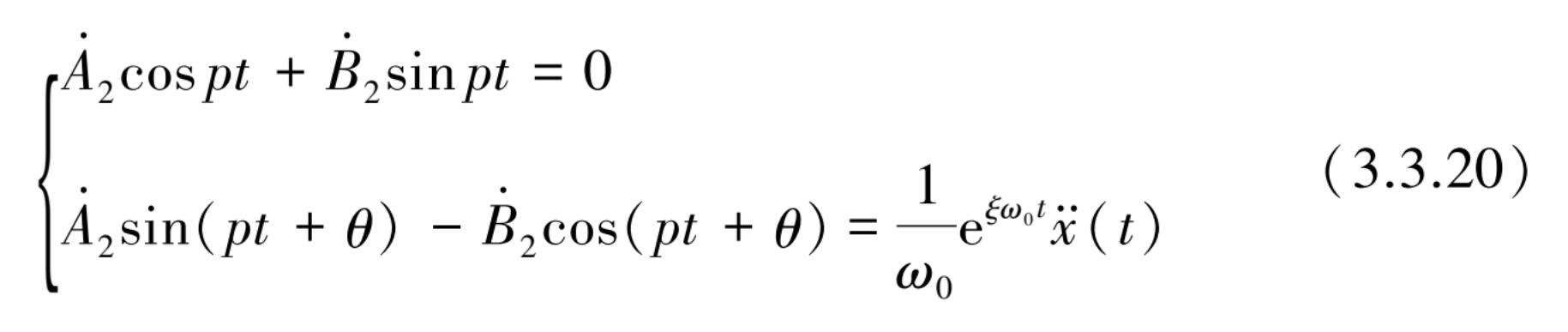
这里第二个方程还可化简为
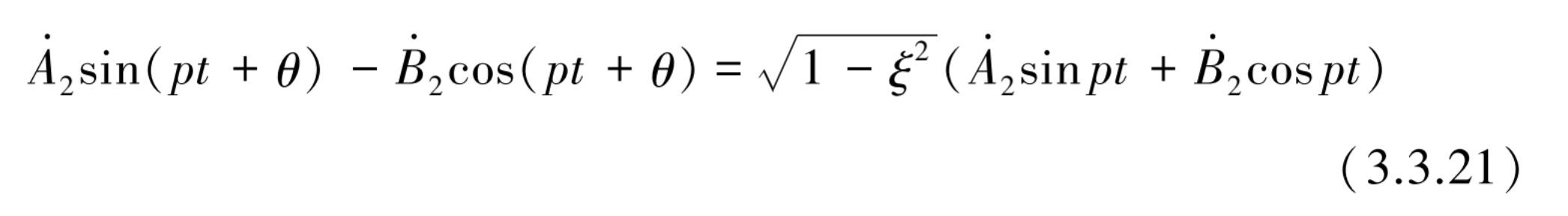
式(3.3.20)变成为
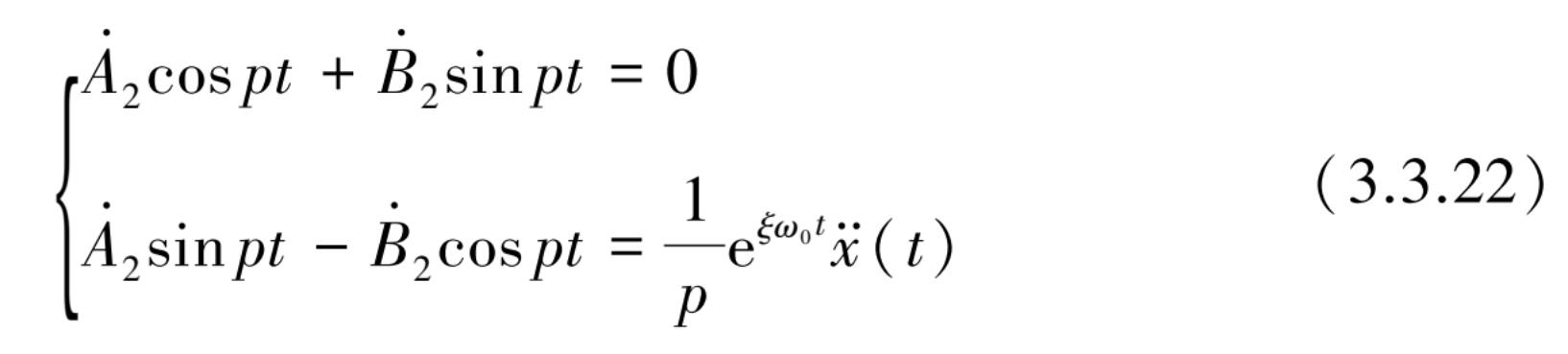
由此可求得
 和
和
 为
为
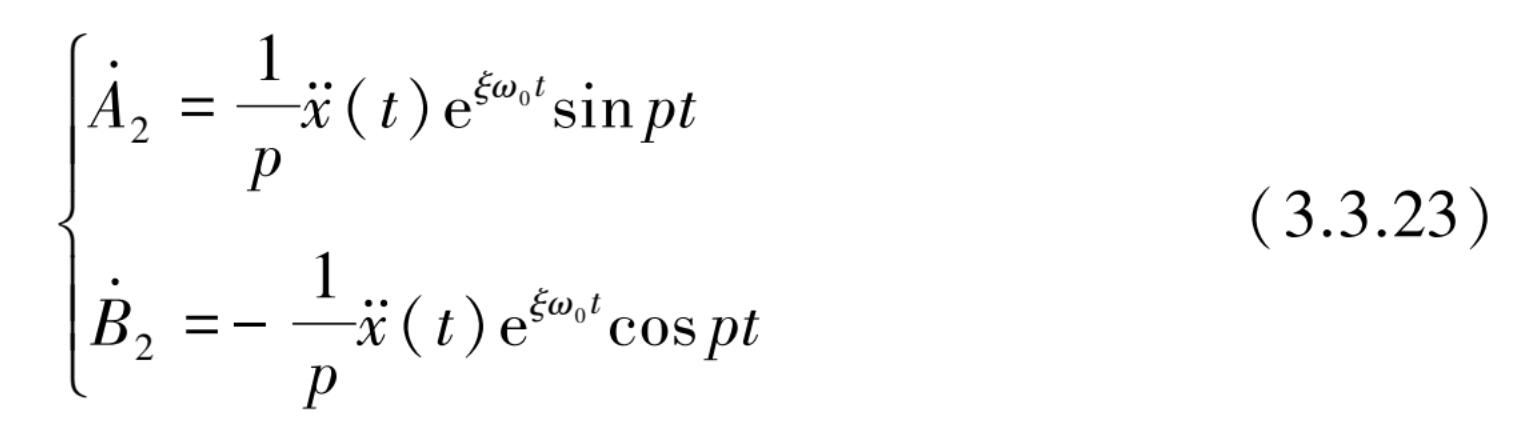
将 A 2 , B 2 定为(0, t )域内对 τ 的定积分后,得到 A 2 和 B 2 为
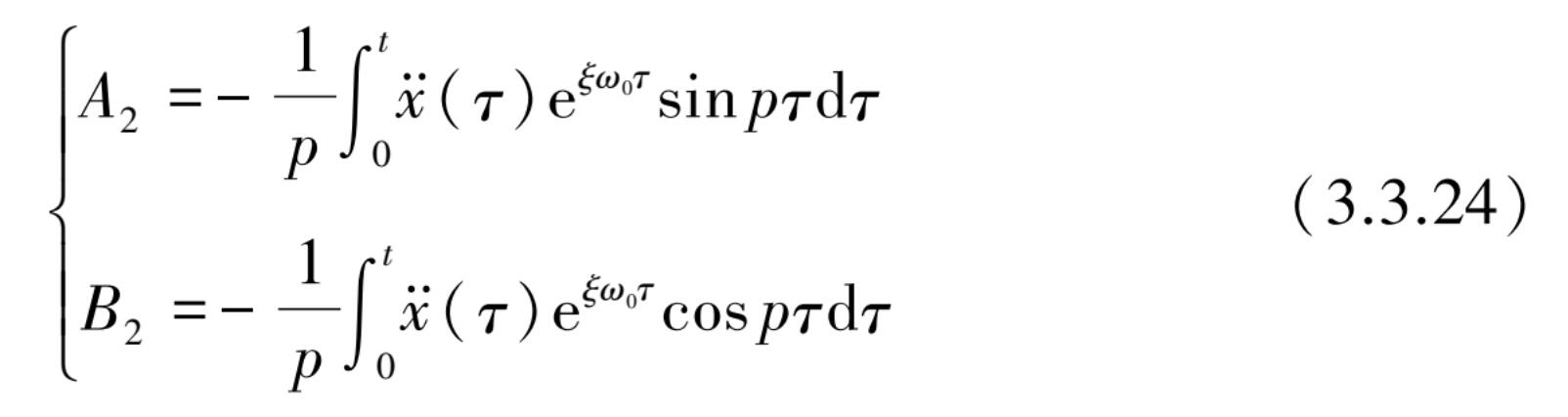
代入式(3.3.13)并整理后得到特解 y 2 ( t )为
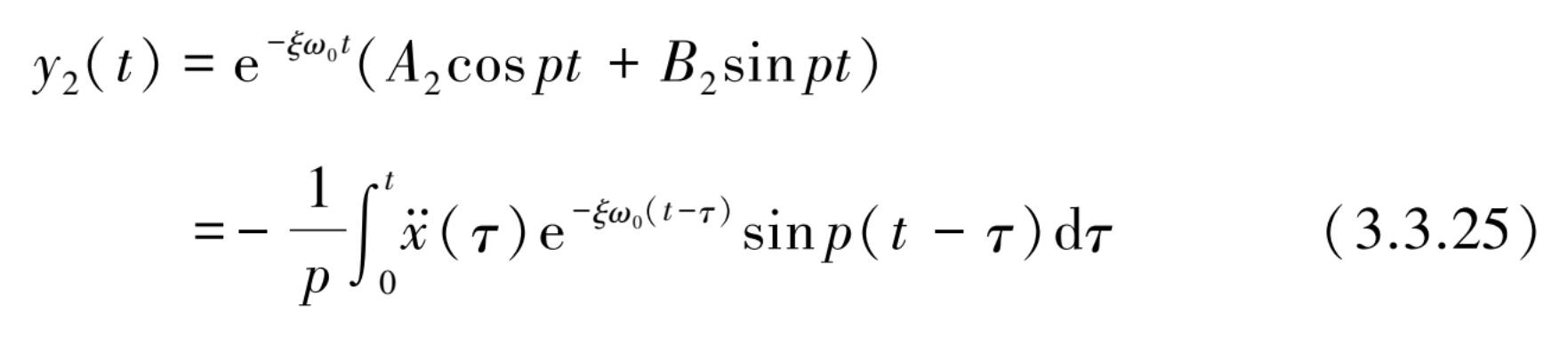
将 A 2 , B 2 代入式(3.3.14)整理后得
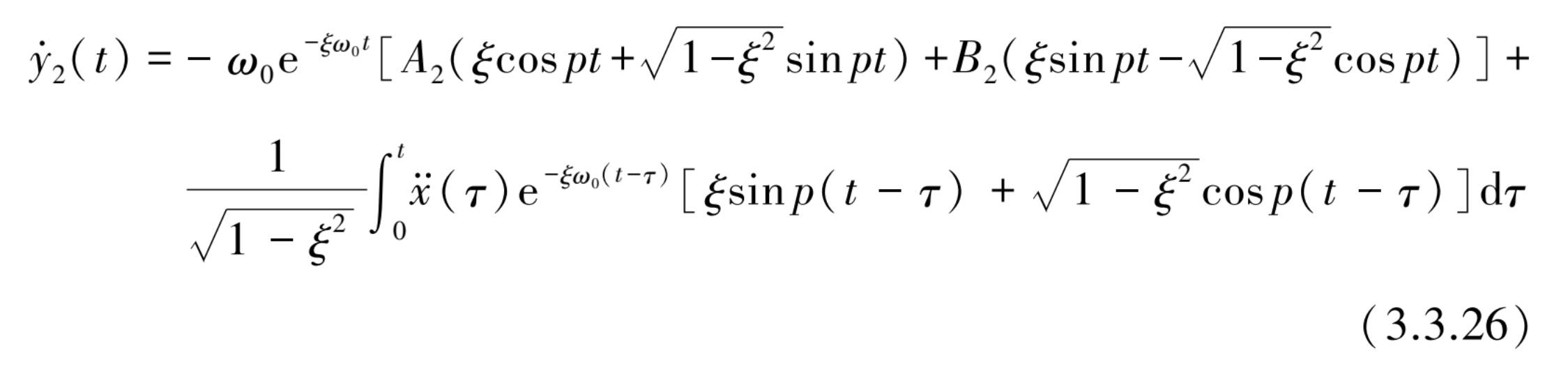
将
y
2
和
 代入式(3.3.7)后可得绝对加速度
代入式(3.3.7)后可得绝对加速度
 的解:
的解:
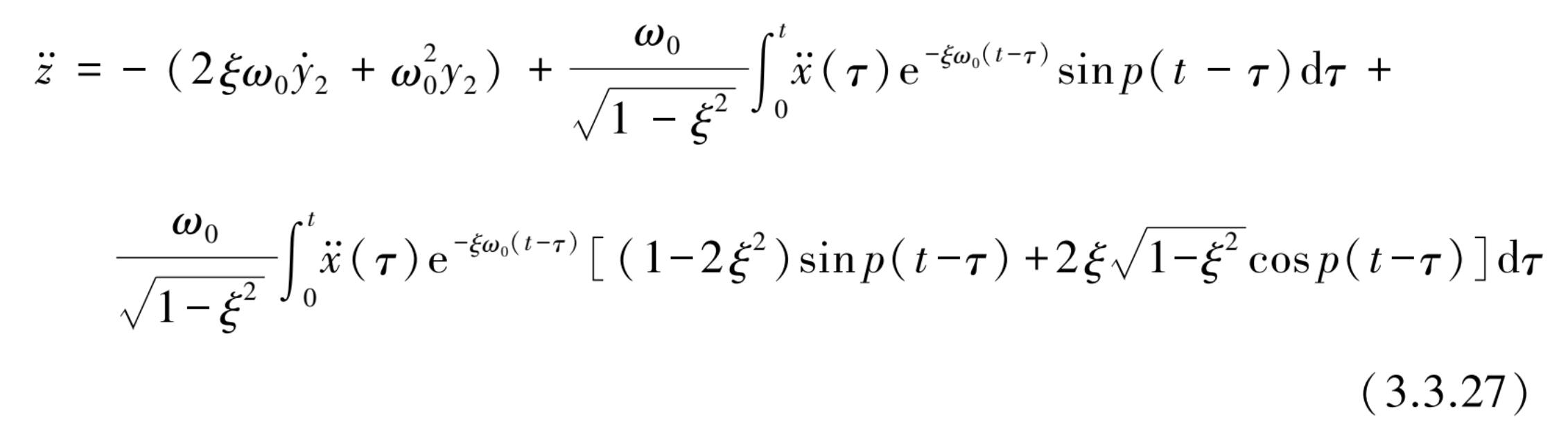
将式(3.3.11)和式(3.3.12)得到的通解
y
1
,
 式(3.3.25)和式(3.3.26)得到的特解
y
2
,
式(3.3.25)和式(3.3.26)得到的特解
y
2
,
 分别代入式(3.3.9)得到
y
和
分别代入式(3.3.9)得到
y
和
 的全解为
的全解为
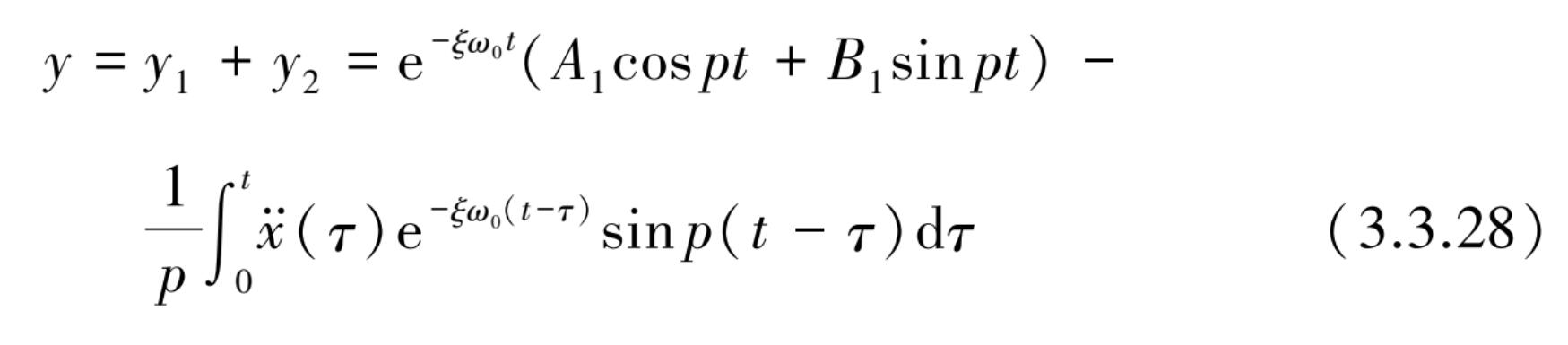
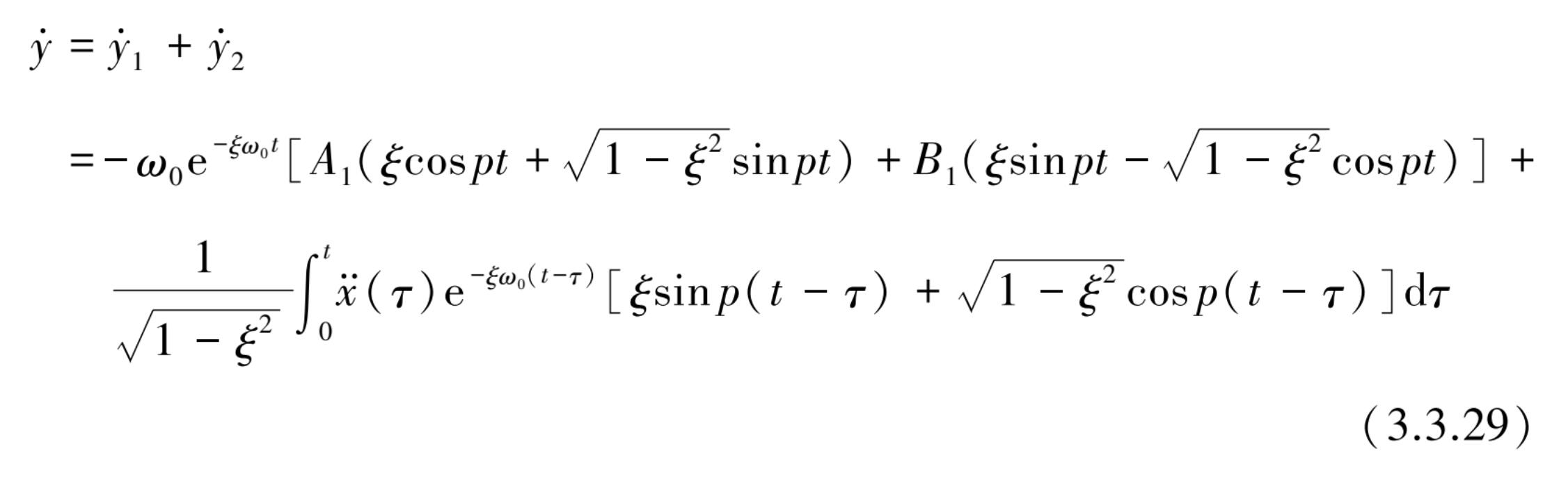
式中,
A
1
和
B
1
积分常数由初始条件
t
=0 时
y
=
y
0
和
 =
=
 =0 来确定,从式(3.3.28)和式(3.3.29)注意到特解
y
2
和
=0 来确定,从式(3.3.28)和式(3.3.29)注意到特解
y
2
和
 在
t
=0 时,
y
2
=
在
t
=0 时,
y
2
=
 =0,因此
A
1
和
B
1
常数与 3.2.4 节中自由振动解完全相同,由式(3.2.13)可推算得到
=0,因此
A
1
和
B
1
常数与 3.2.4 节中自由振动解完全相同,由式(3.2.13)可推算得到
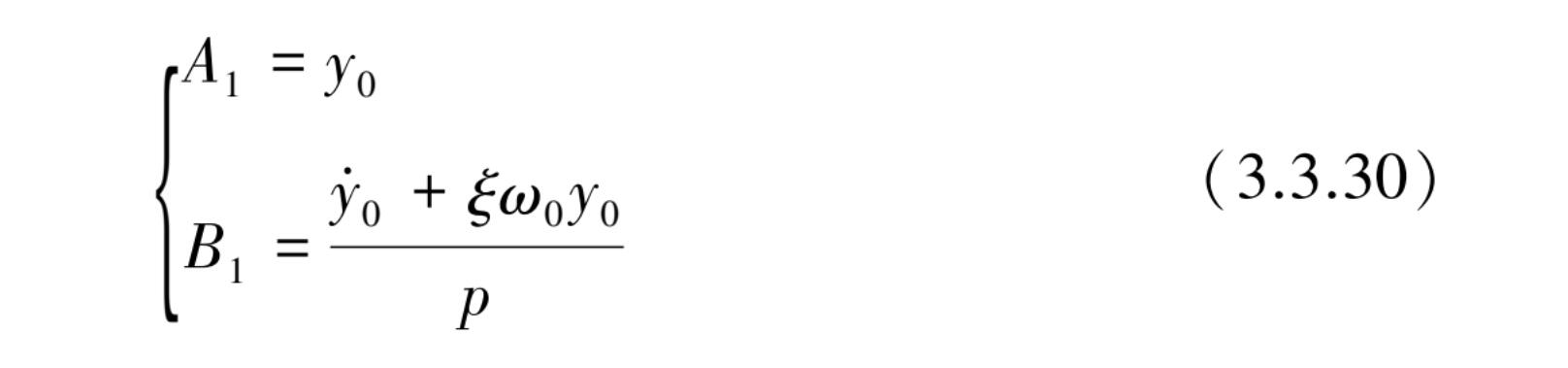
代入式(3.3.28)和式(3.3.29)后整理得到全解
y
和
 为
为
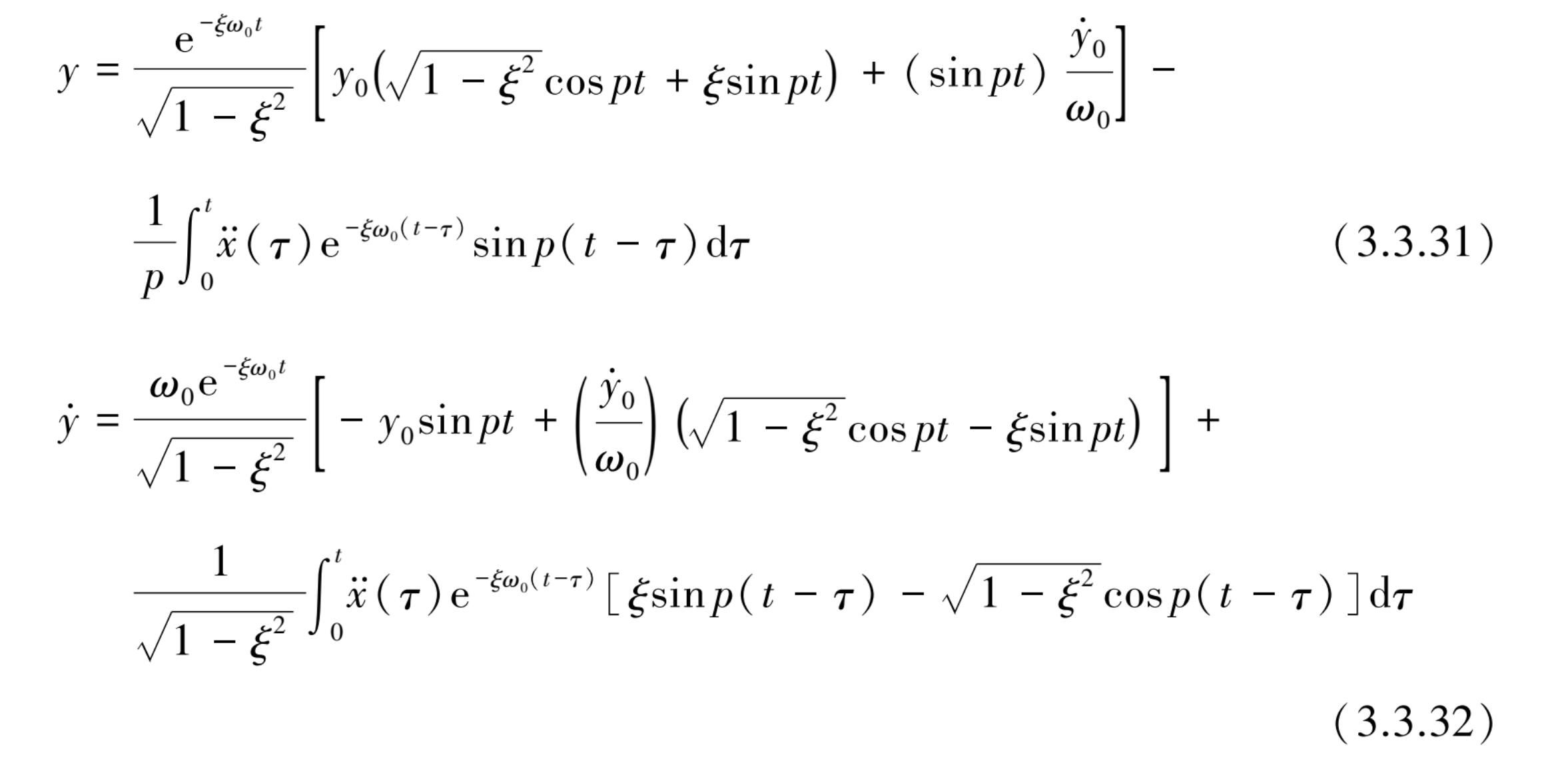
绝对加速度
 为
为
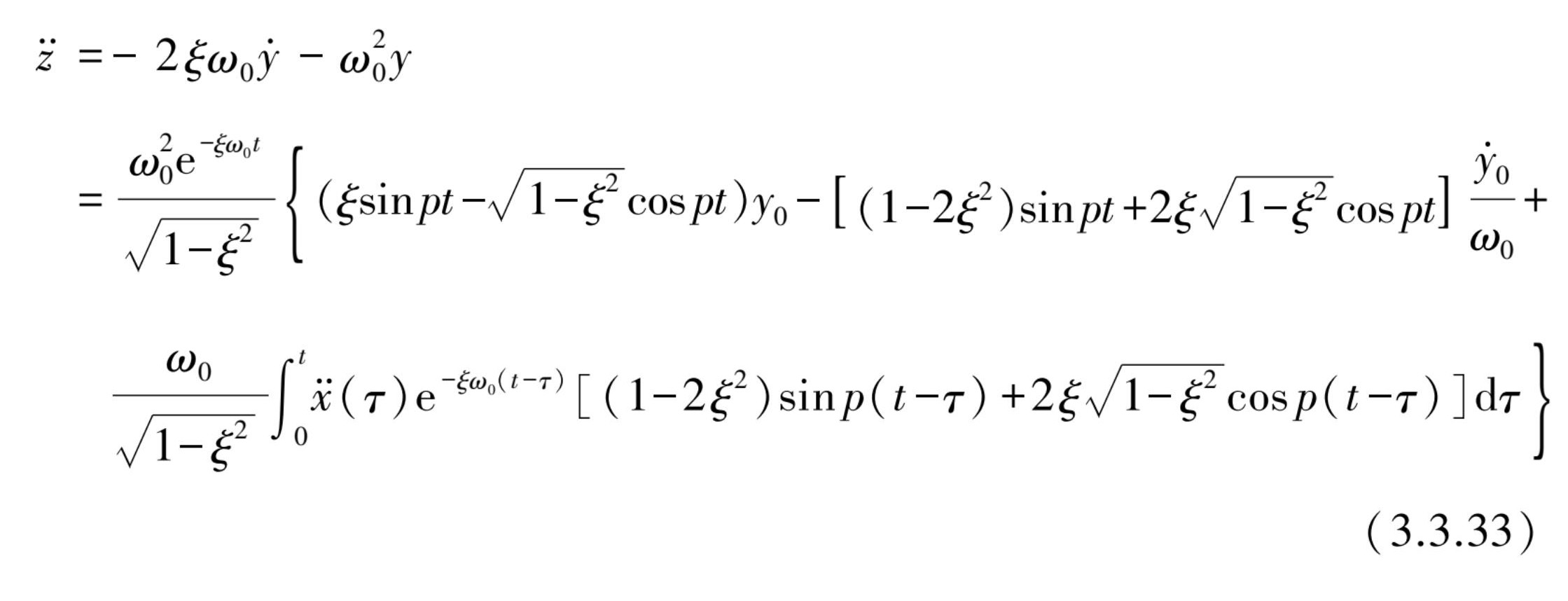
也可用类似式(3.2.24)更简洁的表达式来表示:
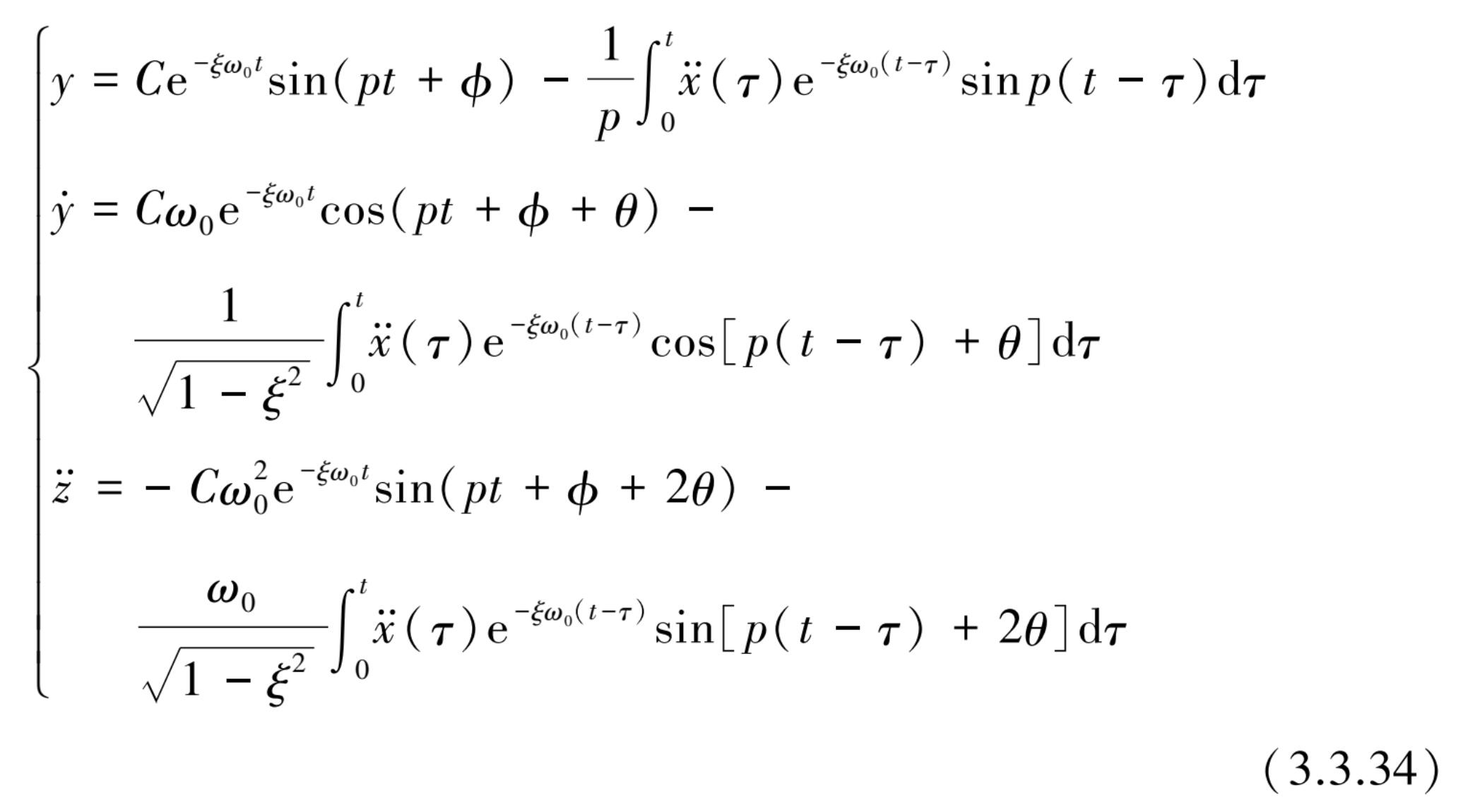
式中,常数
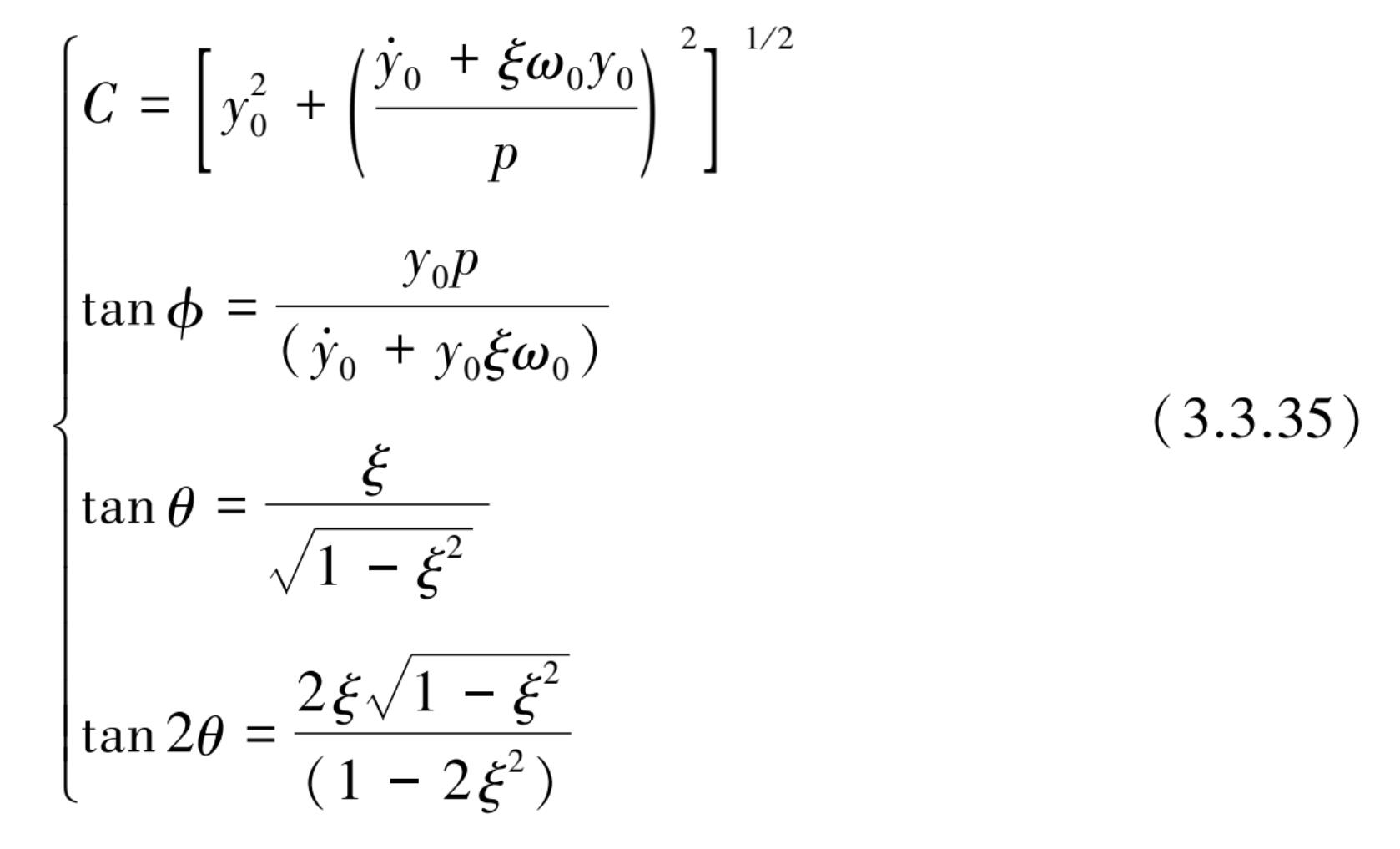
设基础输入加速度时程为简谐激励时,其加速度
 (
t
)为
(
t
)为

式中, a 为谐波振幅, ω 为谐波激励频率。
将式(3.3.36)代入单自由度强迫振动的解式(3.3.31)得到强迫项的积分式特解为
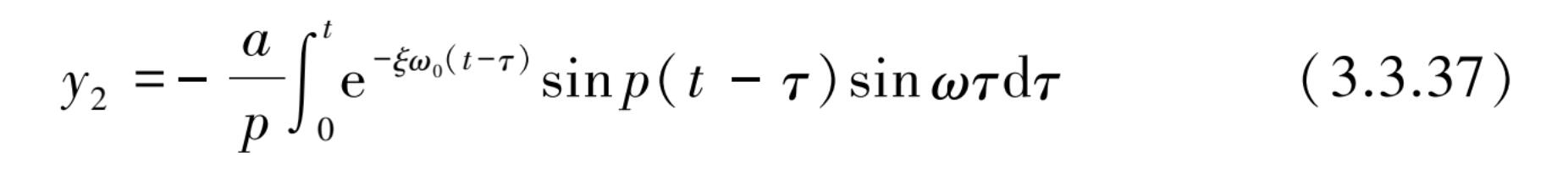
将积分式中 t - τ = t 1 后该积分可变为
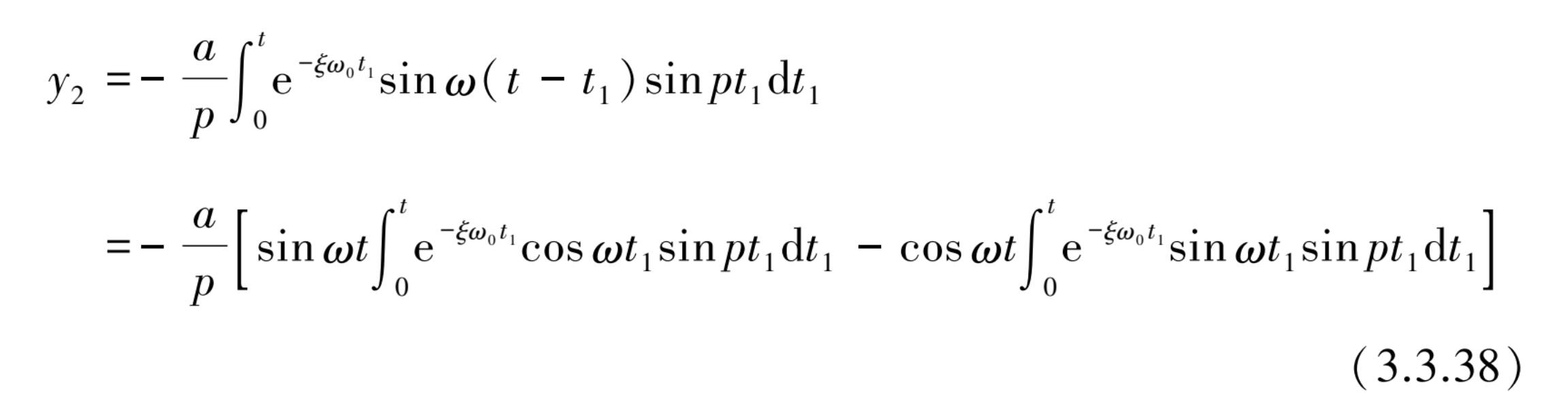
经过推导得到特解
y
2
和
 为
为
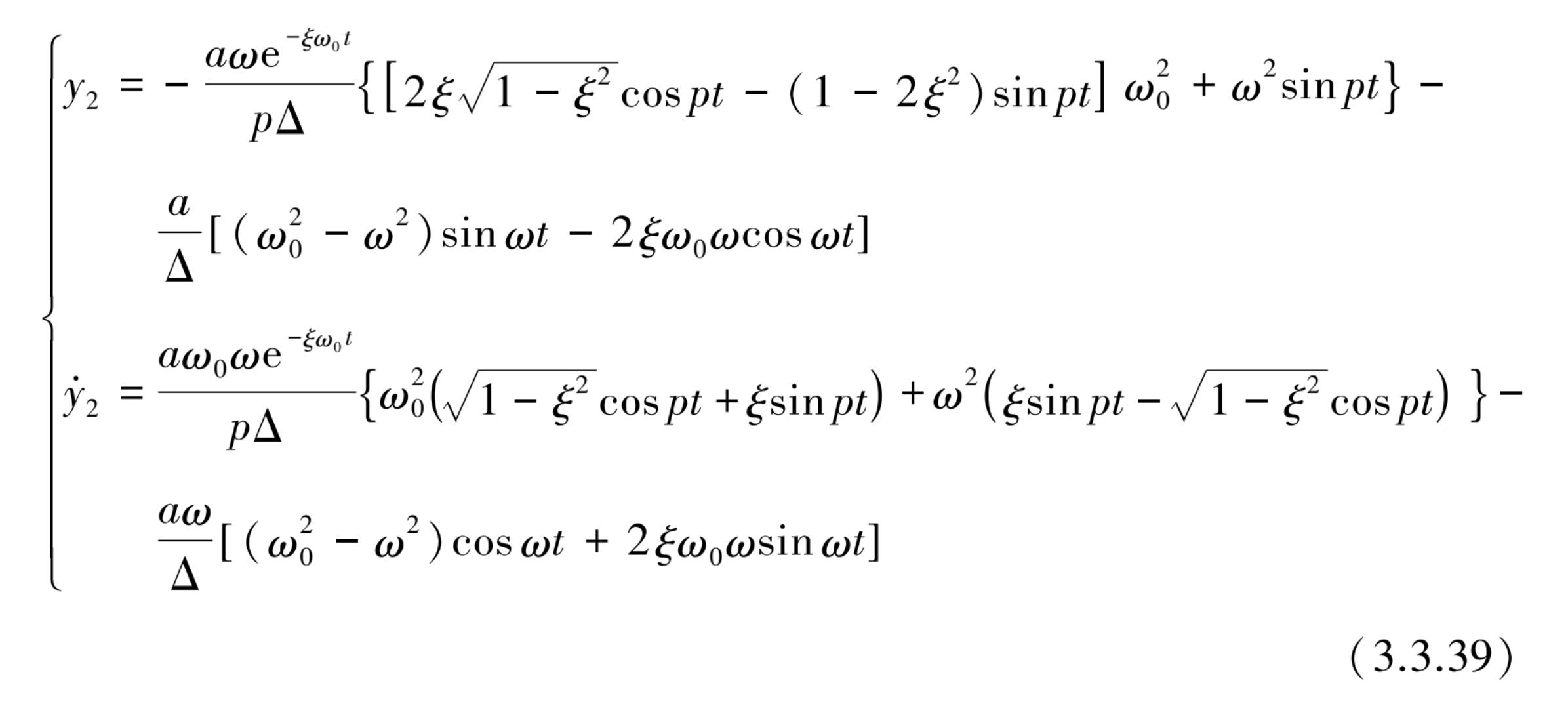
绝对加速度的特解
 为
为
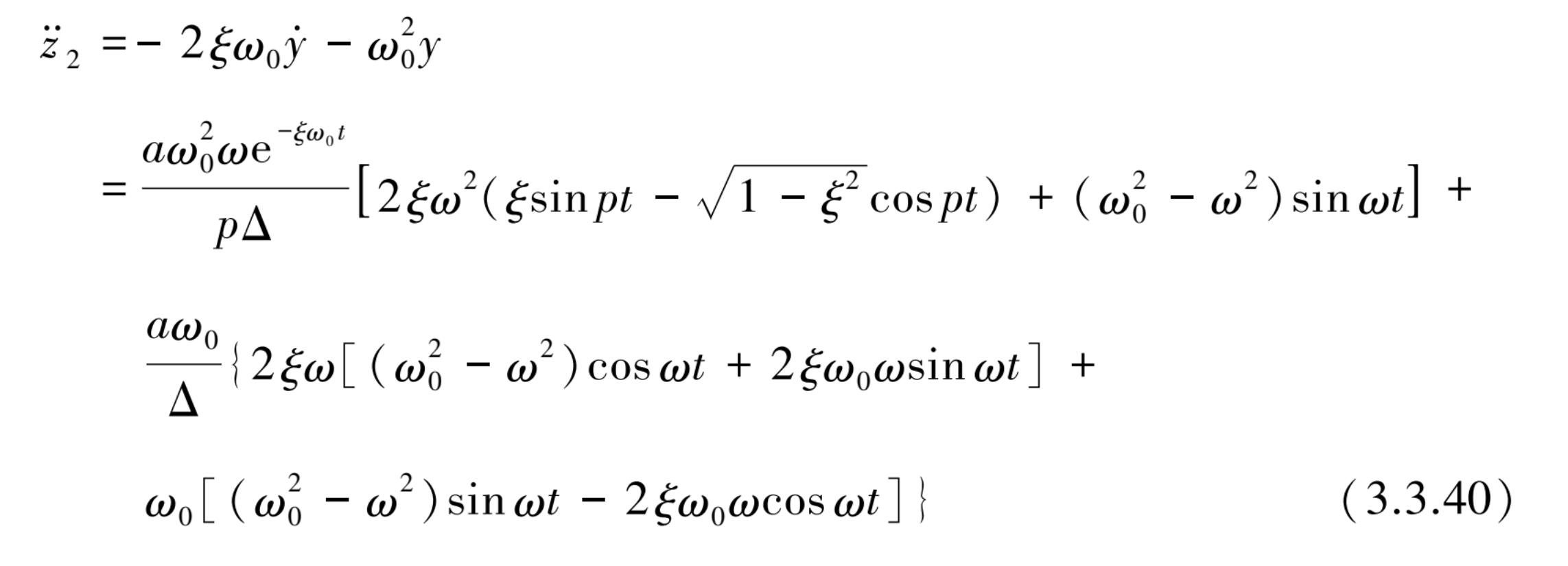
式中,符号Δ和 p 为

从
y
2
,
 和
和
 的结果表达式中可看出两个重要的性质:
的结果表达式中可看出两个重要的性质:
(1)当初始 t =0 代入式(3.3.39)和式(3.3.40)后,得到
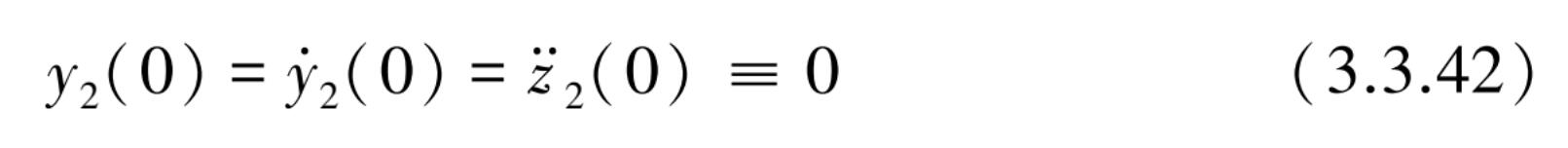
说明振动系统的特解
y
2
,
 和
和
 与初始条件无关,仅由式(3.3.11)和式(3.3.12)的通解
y
1
和
与初始条件无关,仅由式(3.3.11)和式(3.3.12)的通解
y
1
和
 来确定积分常数即可,即
来确定积分常数即可,即
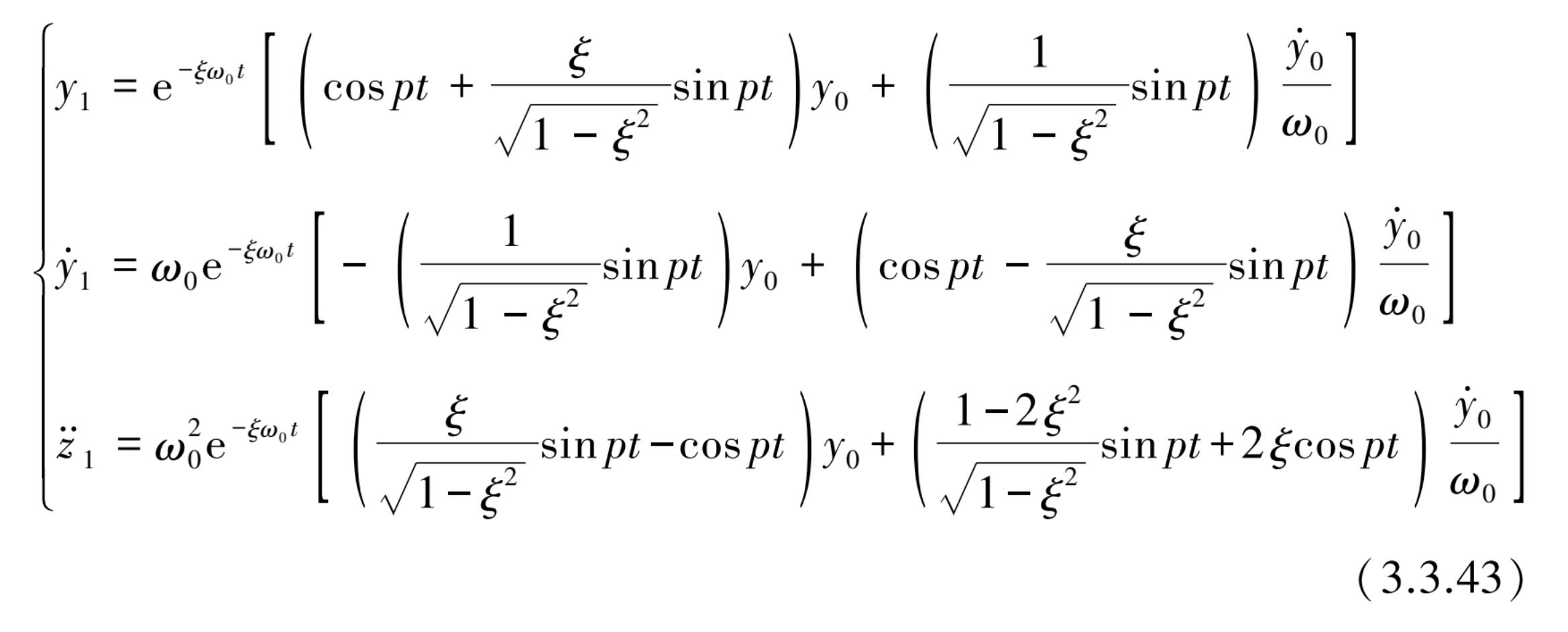
(2)对强迫振动的全解为
y
=
y
1
+
y
2
。第 1 部分
y
1
称为自由振动的解,仅与初始条件
y
0
和
 有关,并以共振频率
p
随时间做振荡的衰减运动。第 2 部分为
y
2
表达式(3.3.39)中右边第 1 项,它是与强迫振动激励频率
ω
有关,但仍以共振频率
p
随时间做振荡的衰减运动,通常称为“伴随强迫项的自由振动”。第 3 部分为
y
2
表达式(3.3.39)右边第 2 项,该项不同于前面两个部分,它以外部激励频率
ω
做周期性变化的无衰减运动,所以它称为“全程性强迫振动”,而当第 1 和第 2 两部分振动按
有关,并以共振频率
p
随时间做振荡的衰减运动。第 2 部分为
y
2
表达式(3.3.39)中右边第 1 项,它是与强迫振动激励频率
ω
有关,但仍以共振频率
p
随时间做振荡的衰减运动,通常称为“伴随强迫项的自由振动”。第 3 部分为
y
2
表达式(3.3.39)右边第 2 项,该项不同于前面两个部分,它以外部激励频率
ω
做周期性变化的无衰减运动,所以它称为“全程性强迫振动”,而当第 1 和第 2 两部分振动按
 衰减后,只剩下第 3 部分无衰减的强迫运动。
衰减后,只剩下第 3 部分无衰减的强迫运动。
图 3.3.3 为位移 y ( t )曲线,其中虚线是按 ω 频率做周期运动的强迫振动;而实线是初始时共振频率为 p 的衰减运动与强迫振动的叠加,它经过一个短时间后,其瞬态的自由振动和伴随振动由于阻尼原因而消失,剩下稳态的周期性强迫运动。
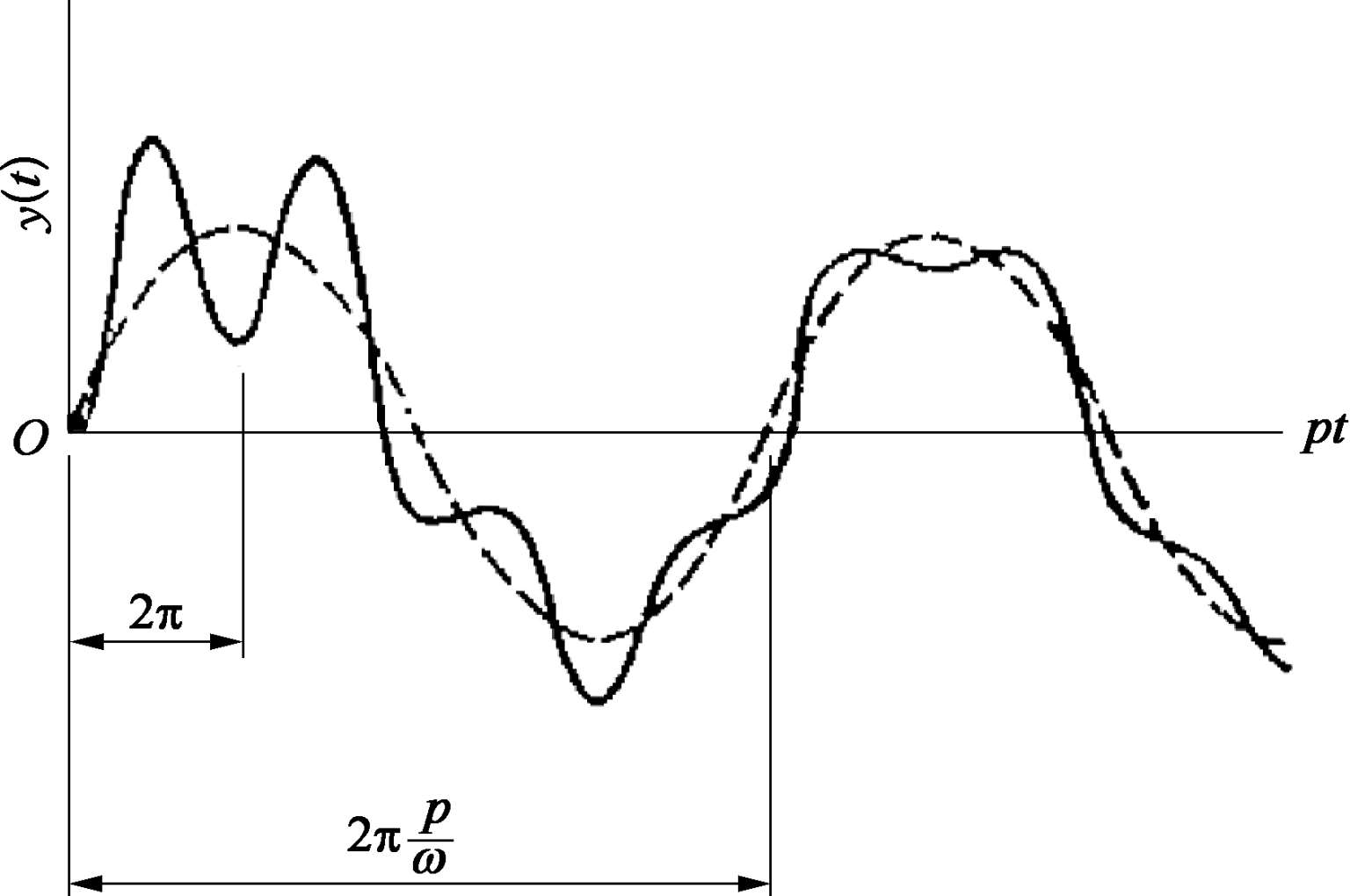
图3.3.3 强迫振动初始阶段
对于式(3.3.43)的自由振动解
y
1
,
 和
和
 也可用更简洁的方式来表达:
也可用更简洁的方式来表达:
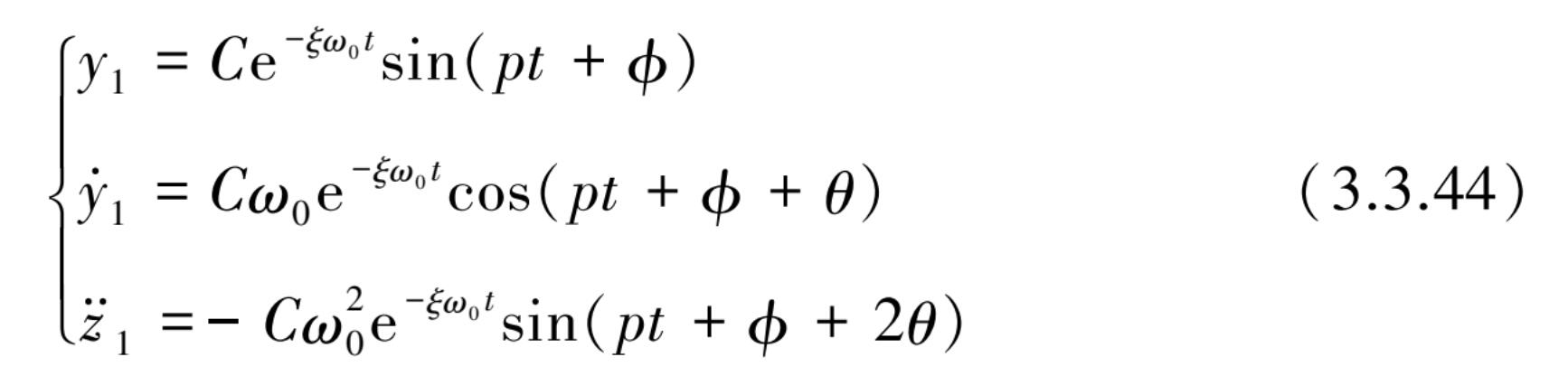
式中,
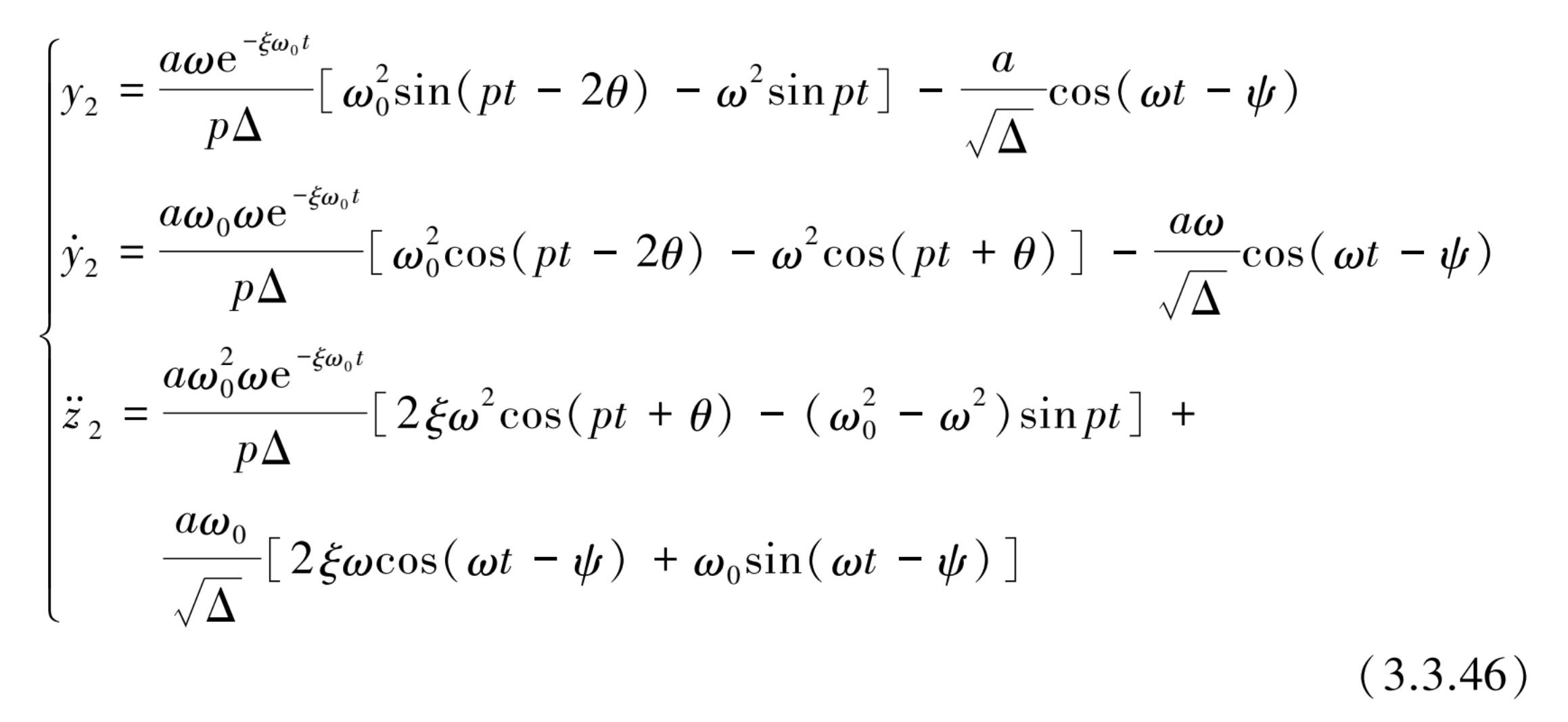
对于式(3.3.39)和式(3.3.40)的强迫振动解 y 2 也可用更简洁的方式来表达:
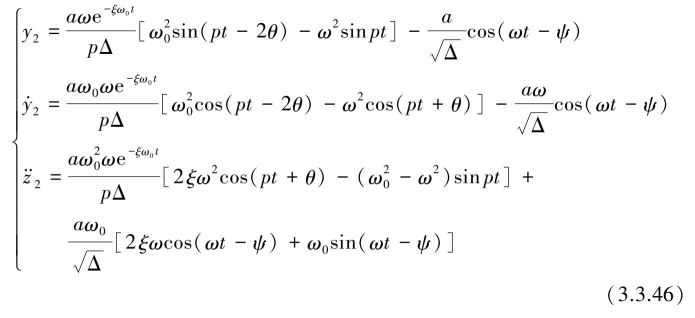
式中,

其余符号同式(3.3.45)和式(3.3.41)。
当基础激励加速度的频率 ω 与系统固有频率 ω 0 相等时,该系统会发生共振,将 ω = ω 0 代入式(3.3.39)和式(3.3.40)后得到
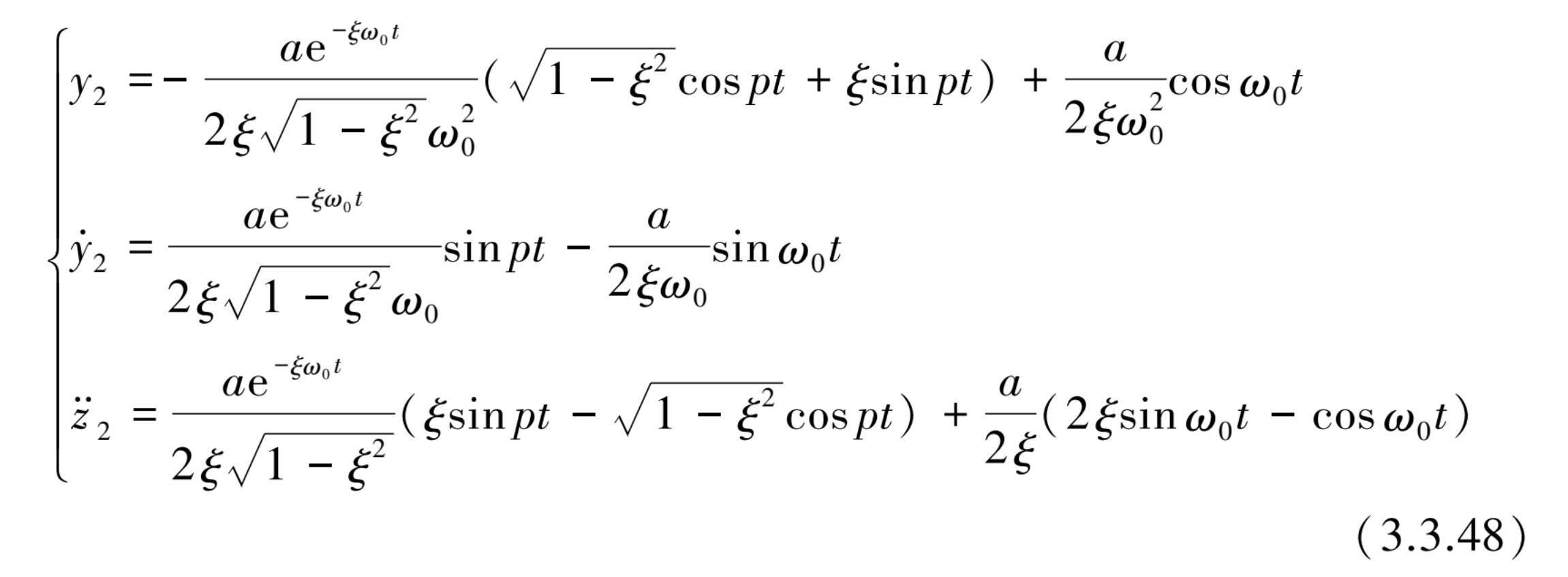
也可用简洁方式表示:
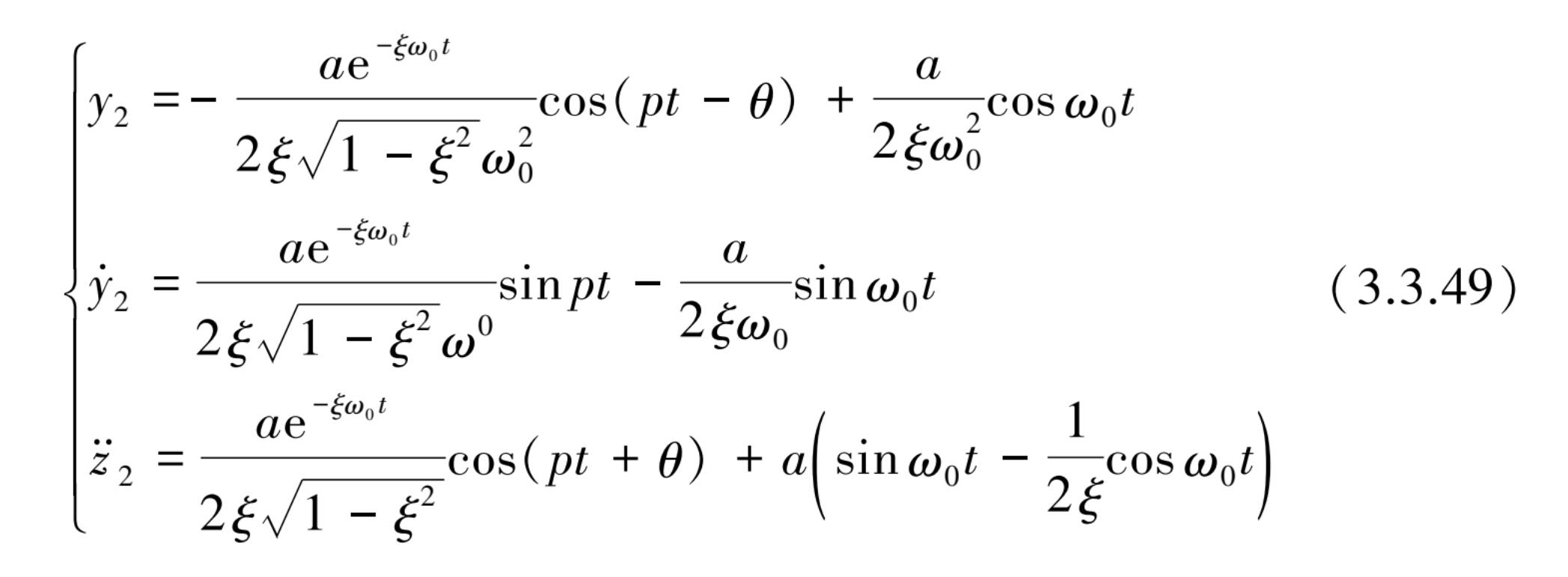
从上式可明显发现,系统在共振时其伴随强迫项或强迫项的振动反应幅值相当于基础输入幅值均放大了
 倍,也就是说振动系统的阻尼比
ξ
愈小,其在共振频率处的幅值反应愈大。
倍,也就是说振动系统的阻尼比
ξ
愈小,其在共振频率处的幅值反应愈大。
如果基础输入加速度时程
 (
t
)为周期性函数,则可以将
(
t
)为周期性函数,则可以将
 (
t
)在周期
T
内展开成傅里叶级数形式。
(
t
)在周期
T
内展开成傅里叶级数形式。

其傅氏系数
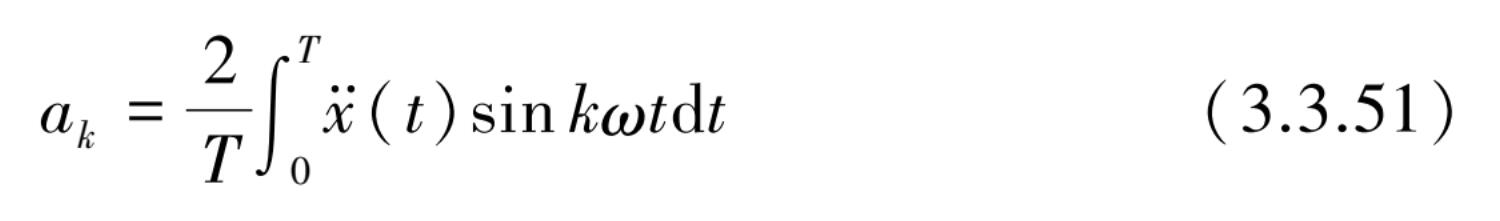
该式表示了基础激励加速度可以分解为 N 个( k ω )圆频率的谐波输入,而单自由度振动系统反应的解可以把幅值 a k 和激励圆频率 ω k = k ω 代入式(3.3.39)和式(3.3.40)的解后,对 k =1,2,…,N的线性叠加即可。
[例]
若输入基础加速度
 (
t
)是一个幅值为
A
、圆频率为
ω
的矩形波(见图 3.3.4),求解强迫振动的解。
(
t
)是一个幅值为
A
、圆频率为
ω
的矩形波(见图 3.3.4),求解强迫振动的解。
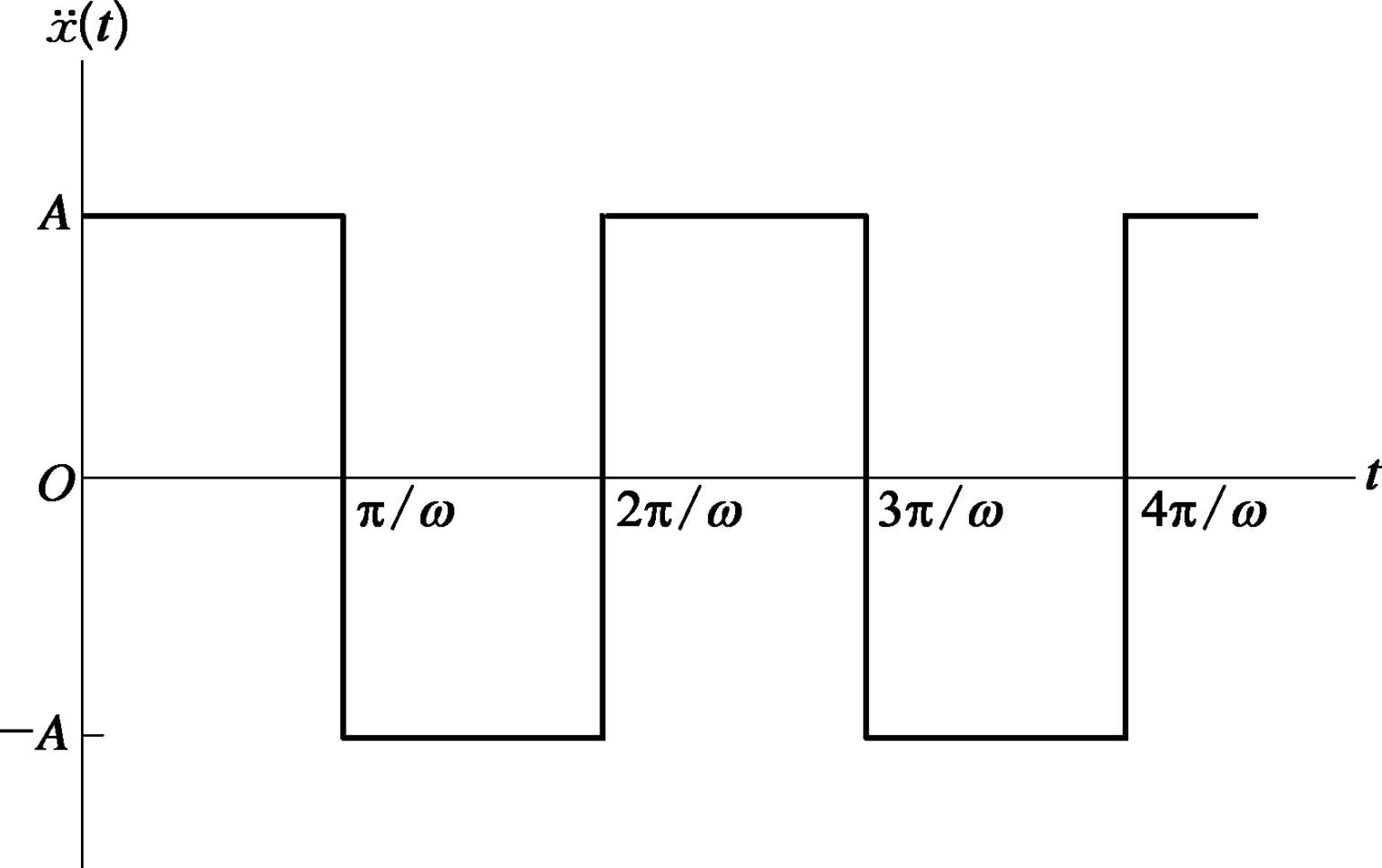
图3.3.4 矩形波的输入加速度
矩形波展开为傅里叶级数可得到
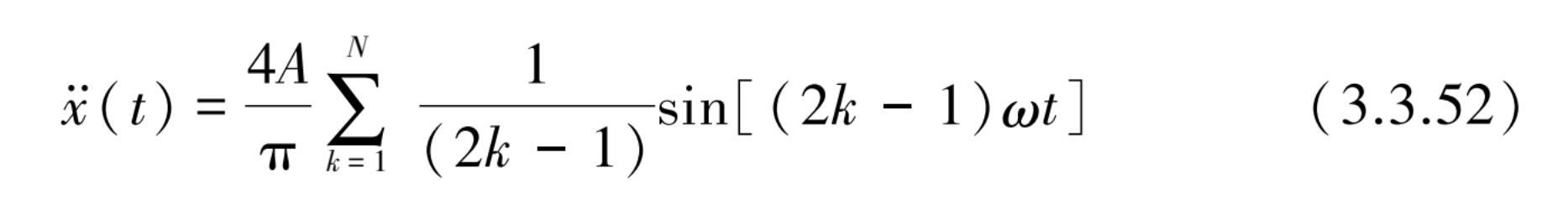
按照式(3.3.51)可得到 a k 为
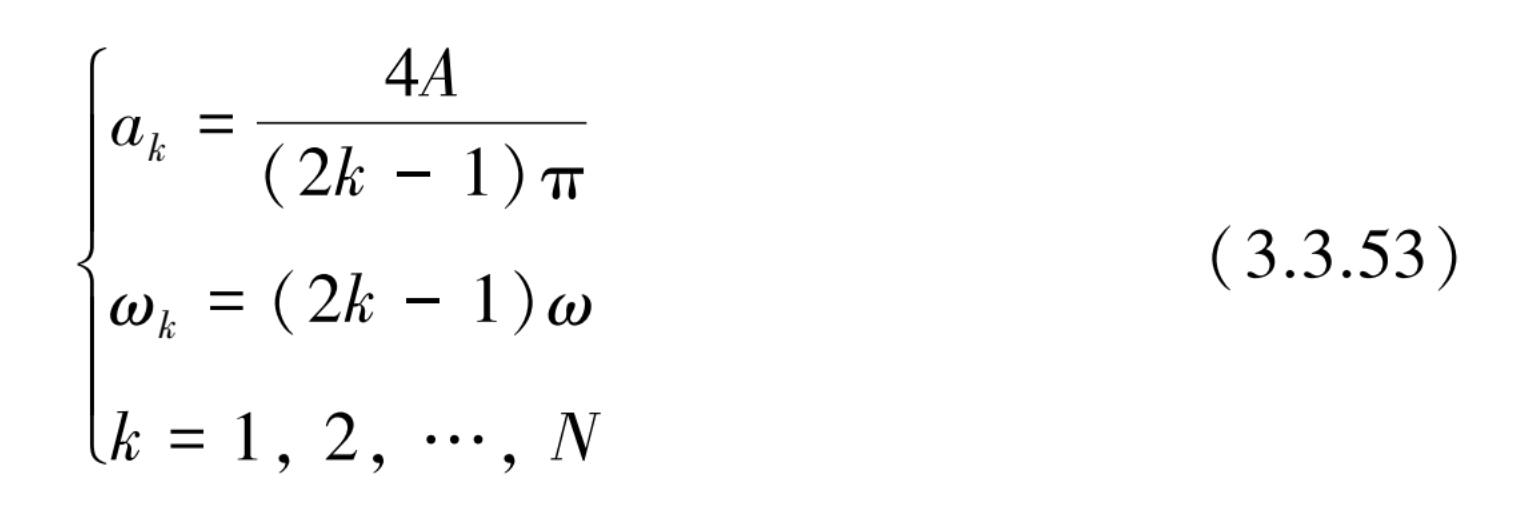
代入式(3.3.46)整理后得特解
y
2
,
 和
和
 为
为
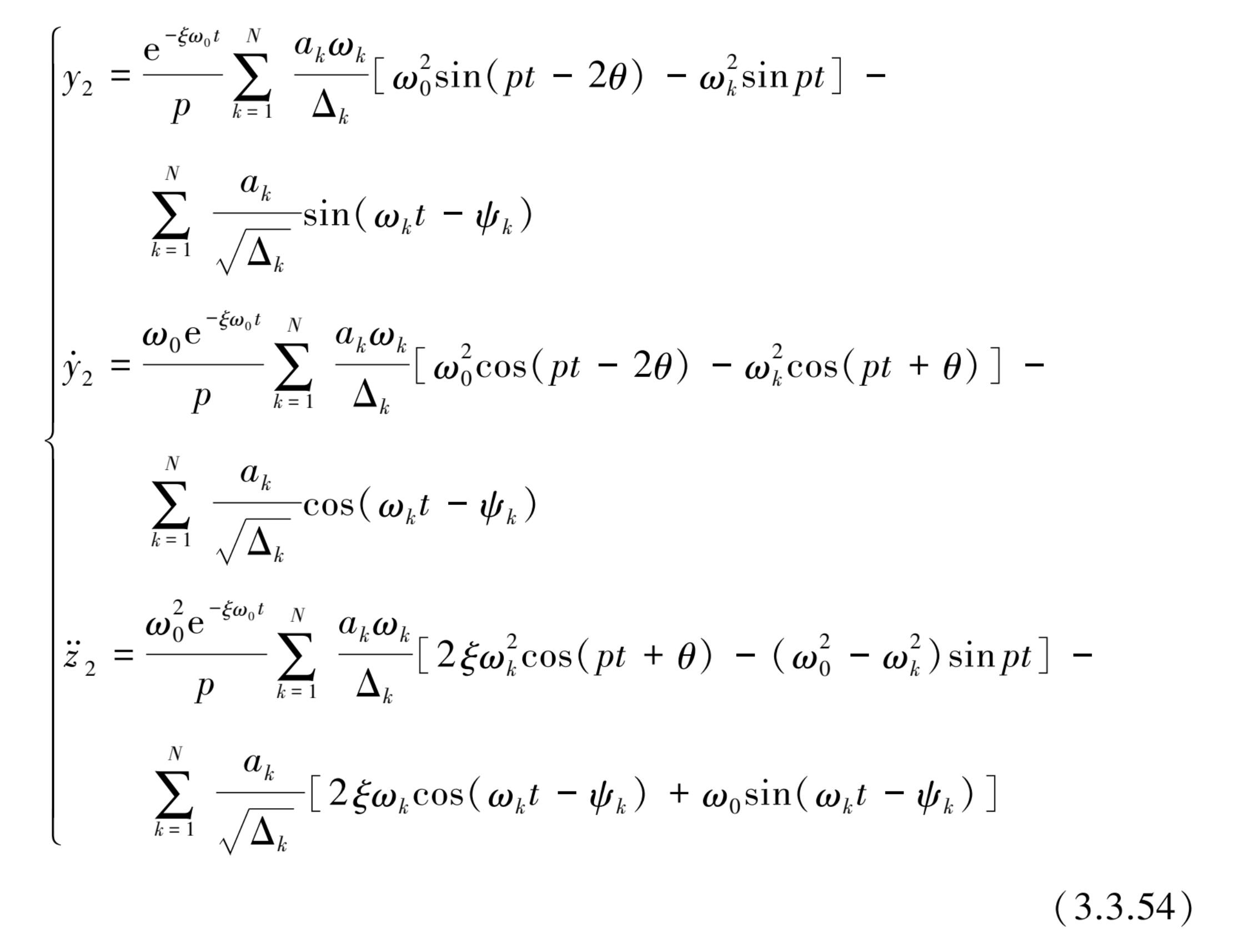
式中,
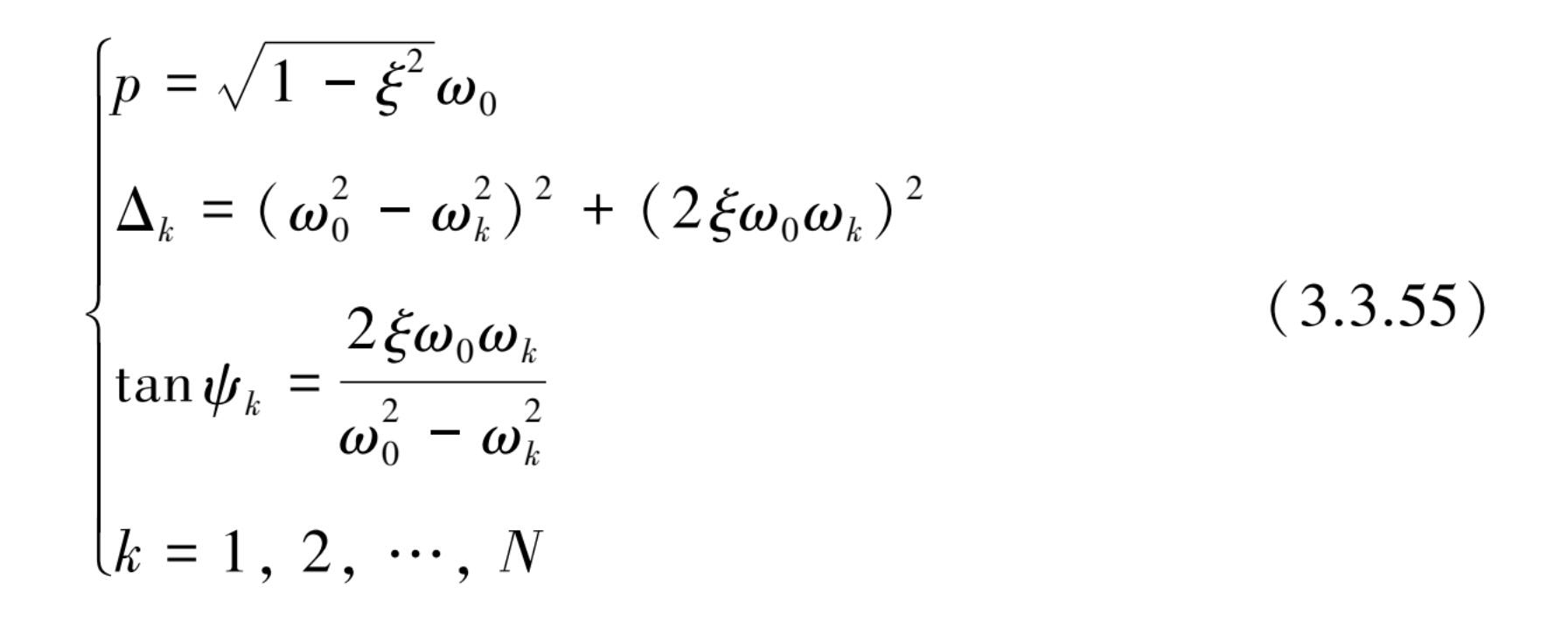
当外部激励频率 ω k =(2 k - 1) ω 与系统共振频率 ω 0 相等时,该系统发生共振。如忽略初期瞬态自由振动和伴随强迫振动的影响,仅考虑稳定阶段后的稳态强迫振动,这时式(3.3.54)中仅考虑第二项强迫振动。用 ω k = ω 0 代入得到稳态强迫振动的最大幅值的近似值。
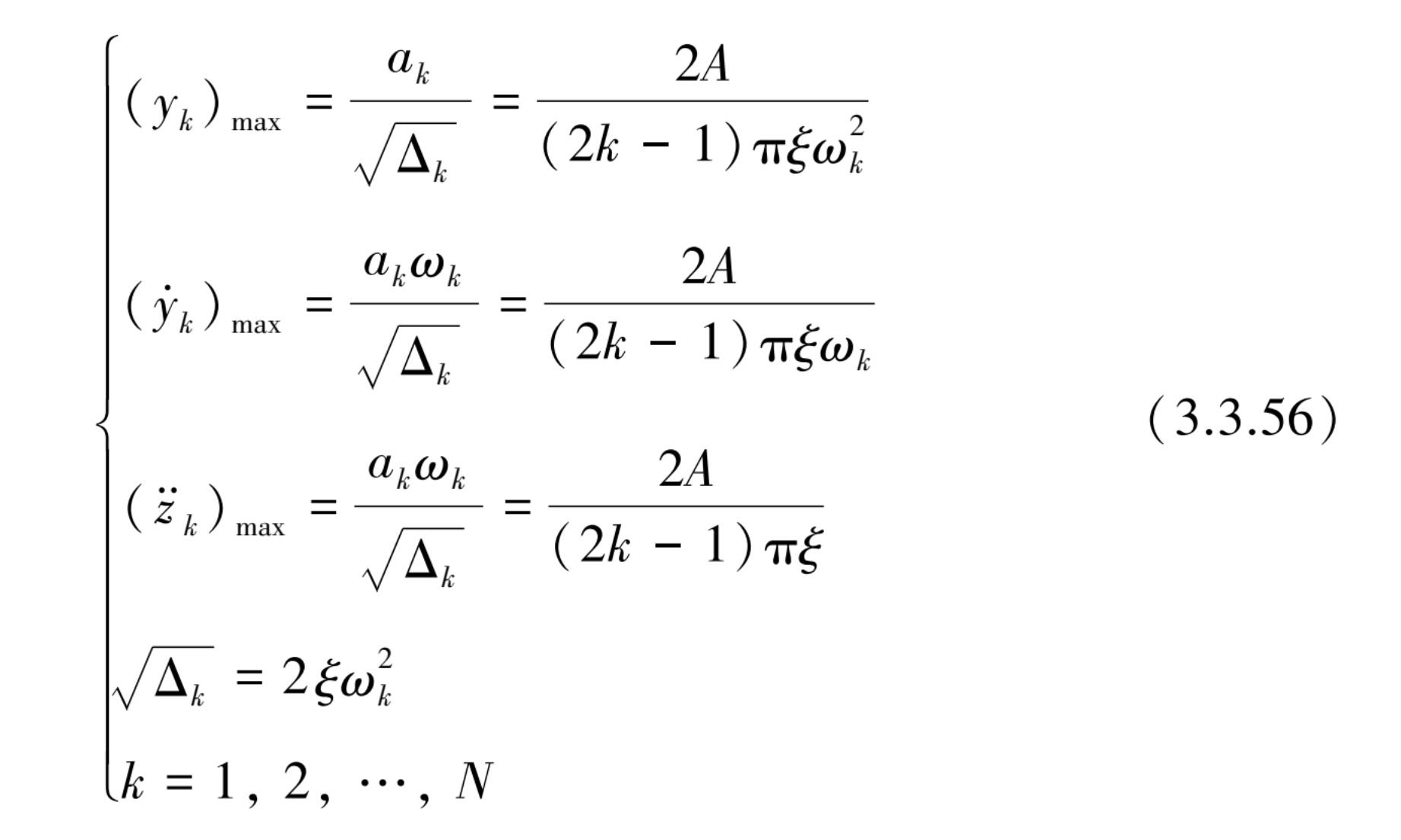
上式近似最大幅值结果可作为求解地震反应谱时的一个十分有用的参考,以实证所编制的地震反应谱求解器或专用程序的计算结果是否可信,并可求其不确定性的误差有多大。
3.3.3 节已阐述单自由度振动系统基础加速度
 (
t
)输入作用下的结构的反应
y
2
,
(
t
)输入作用下的结构的反应
y
2
,
 和
和
 的求解方法和结果,从式(3.3.39)、式(3.3.40)或式(3.3.46)可清楚地看出其反应是时间
t
、系统固有圆频率
ω
0
(或固有周期
T
0
)和阻尼比
ξ
的函数,它们随时间不断地变化。从核电厂构筑物、系统和部件(SSC)抗震设计和分析的角度出发,与求解反应时间变化曲线相比,从工程角度更希望知道的是反应的最大值,即反应的位移、速度和加速度的最大值是多少。设地震时单质点系产生的最大相对位移反应、最大相对速度反应和最大绝对加速度反应分别为
S
d
,
S
v
和
S
a
,将式(3.3.31)~式(3.3.33)中忽略伴随强迫振动随时间变化衰减的影响后可变换为
的求解方法和结果,从式(3.3.39)、式(3.3.40)或式(3.3.46)可清楚地看出其反应是时间
t
、系统固有圆频率
ω
0
(或固有周期
T
0
)和阻尼比
ξ
的函数,它们随时间不断地变化。从核电厂构筑物、系统和部件(SSC)抗震设计和分析的角度出发,与求解反应时间变化曲线相比,从工程角度更希望知道的是反应的最大值,即反应的位移、速度和加速度的最大值是多少。设地震时单质点系产生的最大相对位移反应、最大相对速度反应和最大绝对加速度反应分别为
S
d
,
S
v
和
S
a
,将式(3.3.31)~式(3.3.33)中忽略伴随强迫振动随时间变化衰减的影响后可变换为
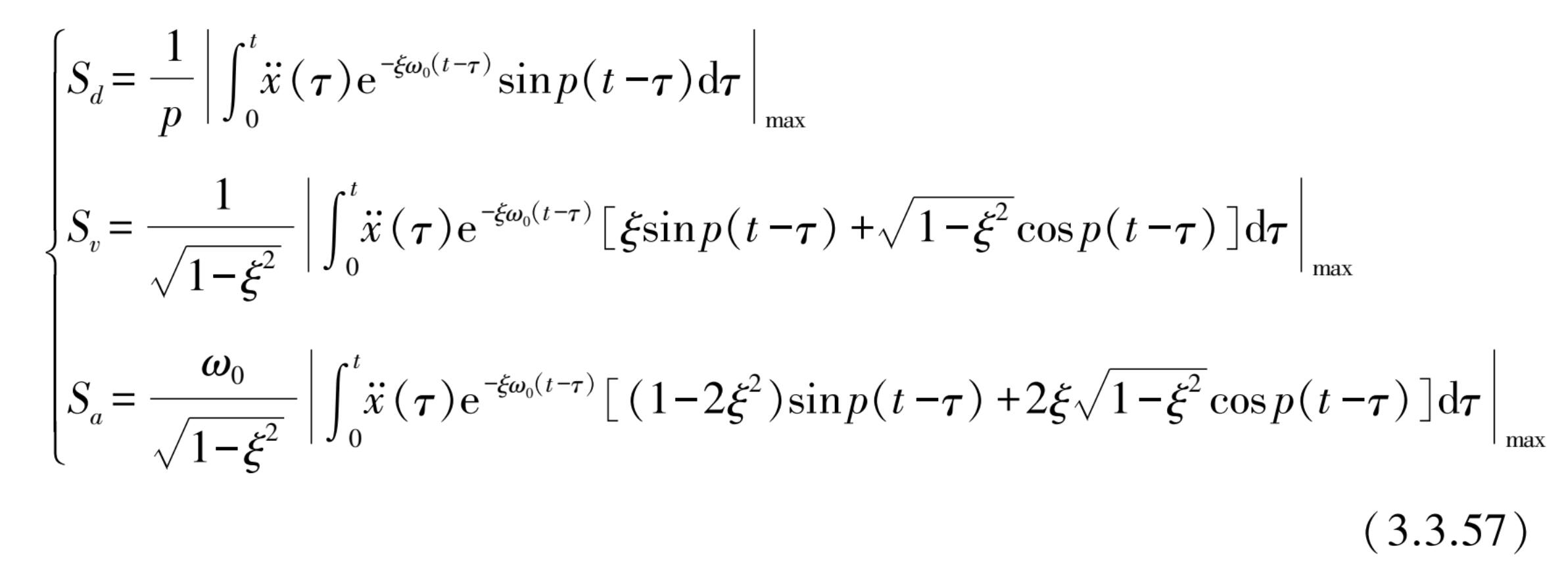
当输入基础的地震加速度时间历程给定后,式(3.3.57)是 ω 0 ( f 0 或 T 0 )和 ξ 的函数,即为 S d ( ξ , T 0 )、 S v ( ξ , T 0 )和 S a ( ξ , T 0 )。
以阻尼比 ξ 为参数,这些函数 S d , S v 和 S a 对无阻尼比固有周期 T 0 (或固有频率 f 0 )所描绘的图分别称为相对位移反应谱、相对速度反应谱和绝对加速度反应谱,总称为地震反应谱,或分别简称为位移反应谱、速度反应谱、加速度反应谱,总称为反应谱。
地震反应谱在ASME BPVC第Ⅲ卷,第 1 册附录N-1110 中定义为一族理想线性、单自由度、有阻尼振子上的最大反应(加速度、速度或位移)曲线,反映了当振子在其支承处有特定的振动运动输入时,其反应与固有频率(或周期)发生的函数关系。
地震反应谱生成的基本概念可用图 3.3.5 来说明。
步骤 1:如图 3.3.5(a)所示的同一平台台面上安放一系列阻尼比均为
ξ
2
,而固有圆频率
ω
0
(或周期
T
0
)各异的谐振振子,也可理解为一组质量阻尼刚度单自由度振动系统。在图中仅列出 3 个振子,3 个不同周期中
T
01
较短、
T
02
中等和
T
03
较长。它们同在某个地震加速度
 (
t
)激励输入的台面上。
(
t
)激励输入的台面上。
步骤 2:台面上各质点随着台面的运动而出现按不同频率在摇动,显示了对输入加速度的反应,所测得的绝对加速度反应
 (
t
)可得到图 3.3.5(b)中的时程曲线记录。
(
t
)可得到图 3.3.5(b)中的时程曲线记录。
T
01
较短,其反应
 振得也较快;
T
03
较长,其反应
振得也较快;
T
03
较长,其反应
 慢。其振子反应振幅的变化与输入加速度
慢。其振子反应振幅的变化与输入加速度
 (
t
)密切相关,但是振子反应的周期几乎与输入无关,仅与振子本身固有特性有关。
(
t
)密切相关,但是振子反应的周期几乎与输入无关,仅与振子本身固有特性有关。
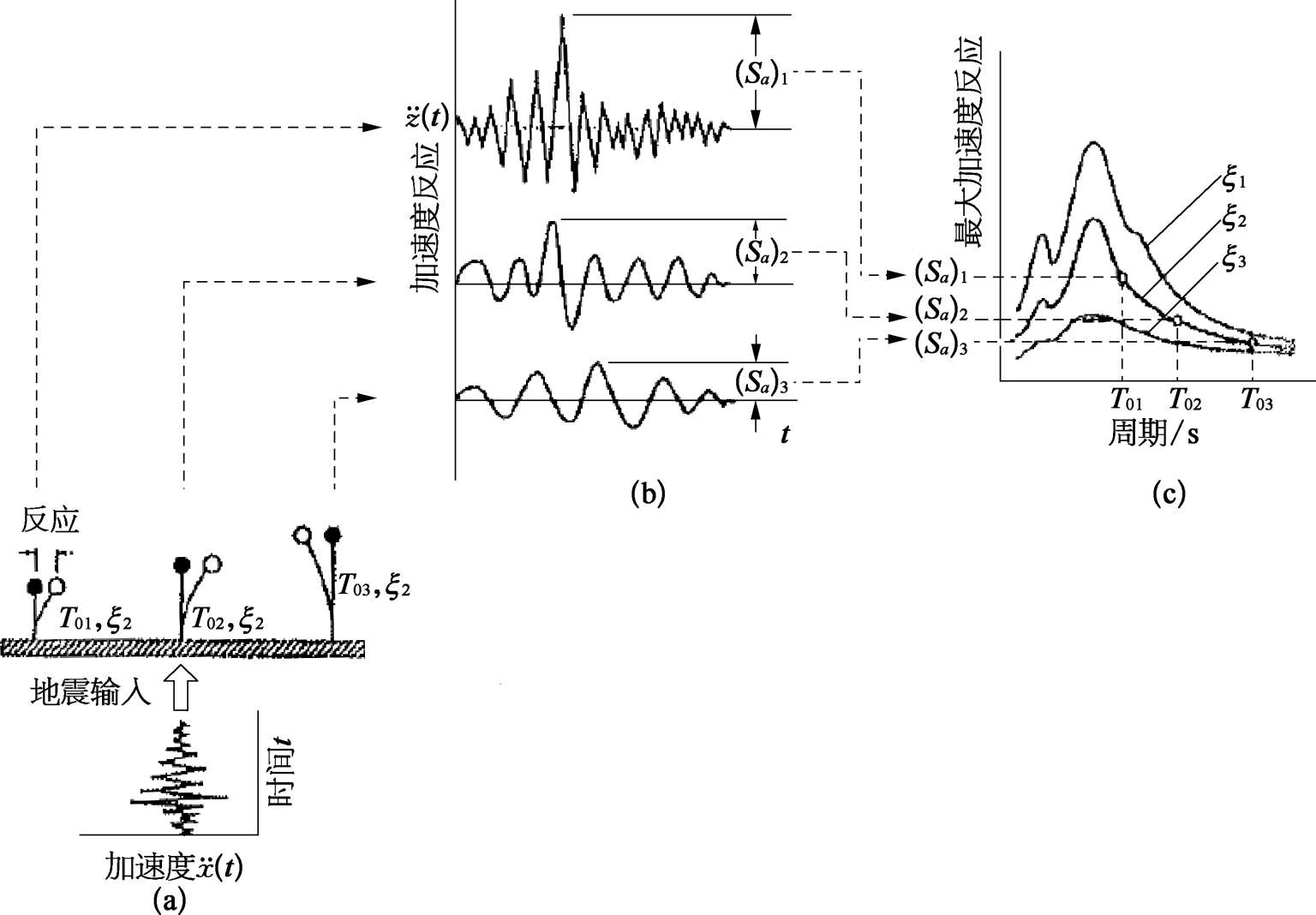
图3.3.5 地震反应谱图解
(a)阻尼比一定,由不同周期 T 0 组成的单质点振动系统;(b)反应波形;(c)反应谱
步骤 3:找出这些加速度时程
 (
t
)上的最大峰值[见图 3.3.5(b)],分别设为(
S
a
)
1
,(
S
a
)
2
和(
S
a
)
3
。在图 3.3.5(c)中横坐标上周期
T
01
,
T
02
和
T
03
处对应纵坐标上以(
S
a
)
1
,(
S
a
)
2
和(
S
a
)
3
对应表示 3 个点。
(
t
)上的最大峰值[见图 3.3.5(b)],分别设为(
S
a
)
1
,(
S
a
)
2
和(
S
a
)
3
。在图 3.3.5(c)中横坐标上周期
T
01
,
T
02
和
T
03
处对应纵坐标上以(
S
a
)
1
,(
S
a
)
2
和(
S
a
)
3
对应表示 3 个点。
步骤 4:当图 3.3.5(a)的基础上并列了众多个周期差别很小的一组单质点系时,就可以得到像图 3.3.5(c)上一条最大加速度 S a 的曲线,而这组单质点振子的阻尼比均为 ξ 2 ,若改变 ξ 值后,再重复上述同样步骤后就可得一簇对应于不同阻尼比 ξ 下的地震最大反应曲线。图 3.3.5(c)所示曲线簇就称为输入地震加速度反应谱。
图 3.3.5 中采用的质点振动反应是加速度
 ,对应可得到加速度反应谱。若采用的质点振动反应是速度
,对应可得到加速度反应谱。若采用的质点振动反应是速度
 、位移
y
(
t
),则按上述同样步骤 1~步骤 4 运算,分别可得到速度反应谱和位移反应谱。
、位移
y
(
t
),则按上述同样步骤 1~步骤 4 运算,分别可得到速度反应谱和位移反应谱。
图 3.3.6 分别列出了某地地震波对应于阻尼比=1%,5%和 10%的加速度反应谱、速度反应谱和位移反应谱。
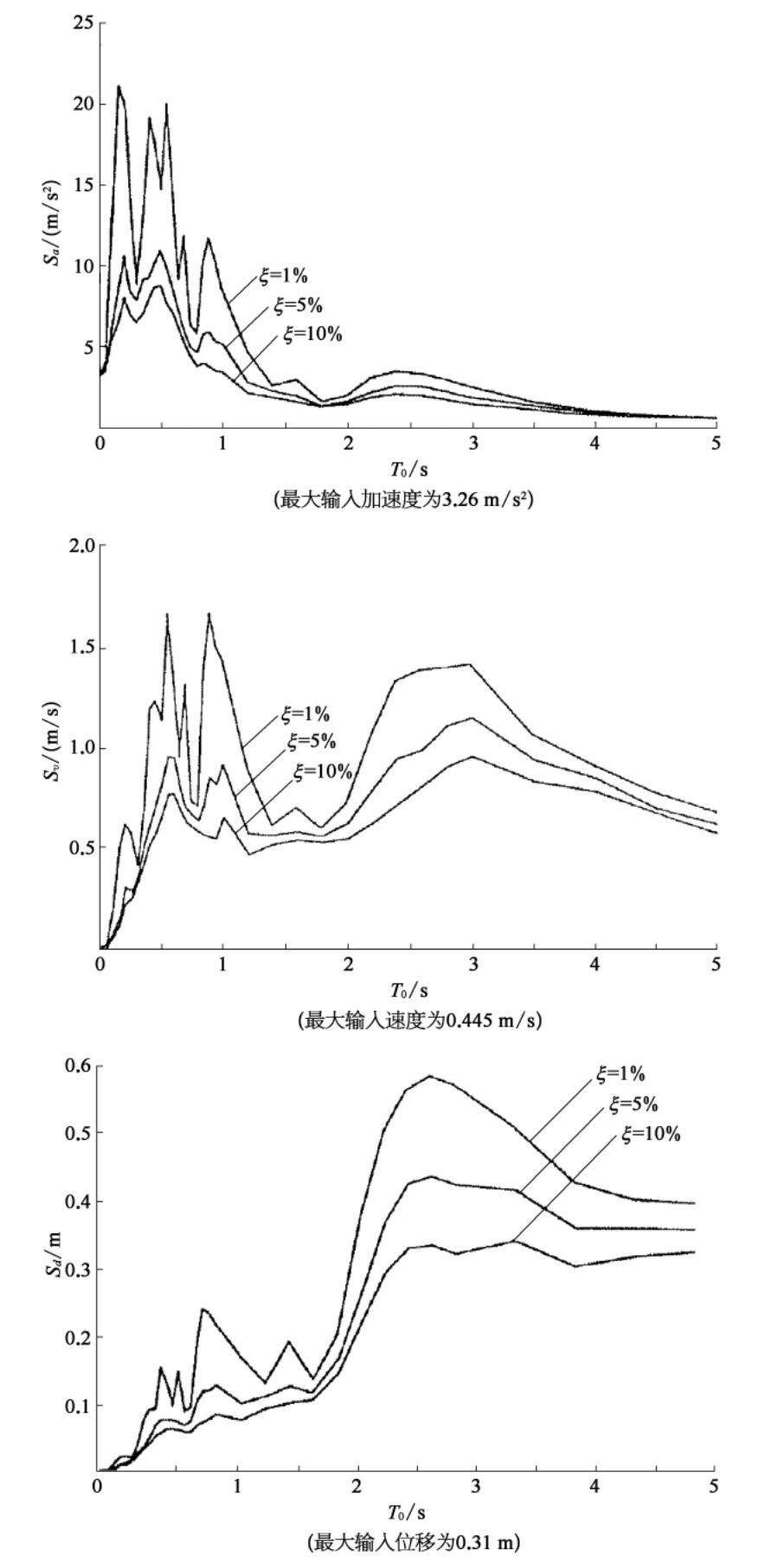
图3.3.6 地震反应谱采用周期表示
本书附录B详细列出了求解加速度反应谱的时间差分格式,用每步时间间隔
h
=
t
n
+1
- t
n
计算下步
t
n+
1
时的位移、速度和加速度时均要计及
t
n
时刻的位移
Y
n
、速度
 作为初始条件,因必须要用到式(3.3.33)中的总解,
y
=
y
1
+
y
2
,
y
=
作为初始条件,因必须要用到式(3.3.33)中的总解,
y
=
y
1
+
y
2
,
y
=
 +
+
 以及式(3.3.33)中的
以及式(3.3.33)中的
 表达式或者采用式(3.3.34)和式(3.3.35)。
表达式或者采用式(3.3.34)和式(3.3.35)。
图 3.3.6 中的加速度、速度和位移反应谱分别采用与固有周期 T 0 的关系来表示,但抗震设计分析时还需要采用不同的表示反应谱图示方法,以便于在不同场合使用。
1)频率域表示方法
有时,反应谱曲线上横坐标不用周期而用频率
 来表示时,适用性更强。如图 3.3.7 是使用频率为横坐标表示的加速度、速度和位移反应谱,对于速度和位移也可以同样的方法来描述,只是常使用频率的对数值。一般在频率达到 33 Hz以上,其加速度反应值最大值与基础输入加速度最大值很接近,在设施抗震设计时称为零周期幅值(ZPA值),即表示了设施的固有频率
f
0
≥ 33 Hz时可近似认为是刚性支承,其加速度反应直接用基础加速度最大峰值进行分析即可。
来表示时,适用性更强。如图 3.3.7 是使用频率为横坐标表示的加速度、速度和位移反应谱,对于速度和位移也可以同样的方法来描述,只是常使用频率的对数值。一般在频率达到 33 Hz以上,其加速度反应值最大值与基础输入加速度最大值很接近,在设施抗震设计时称为零周期幅值(ZPA值),即表示了设施的固有频率
f
0
≥ 33 Hz时可近似认为是刚性支承,其加速度反应直接用基础加速度最大峰值进行分析即可。
2)拟反应谱表示方法
一般核电厂中SSC抗震设计时所采用的阻尼比 ξ 均比 1 小得多,因此可假设:

这时共振圆频率:

那么式(3.3.57)可以简化为
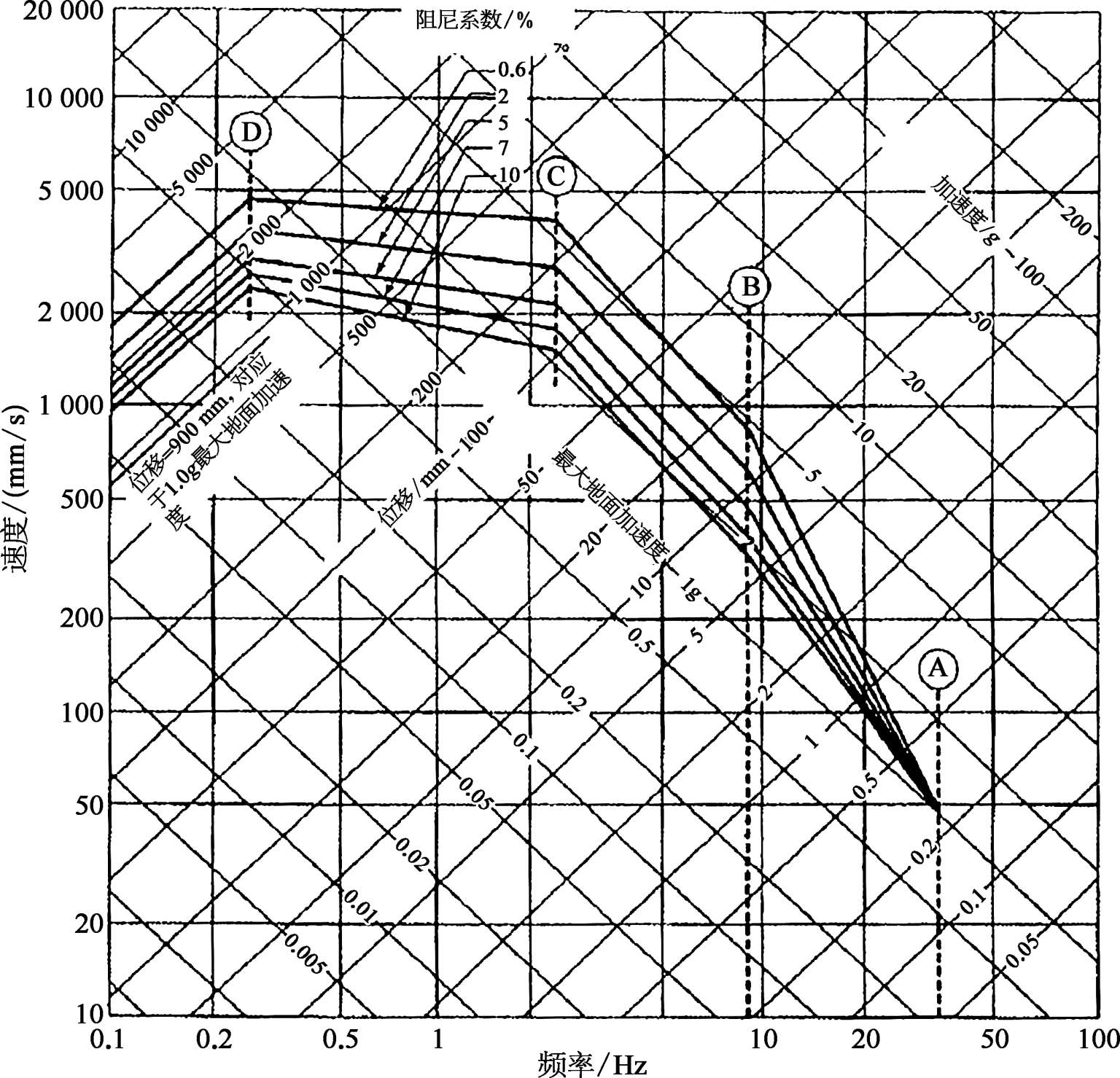
图3.3.7 地震反应谱采用频率表示方法
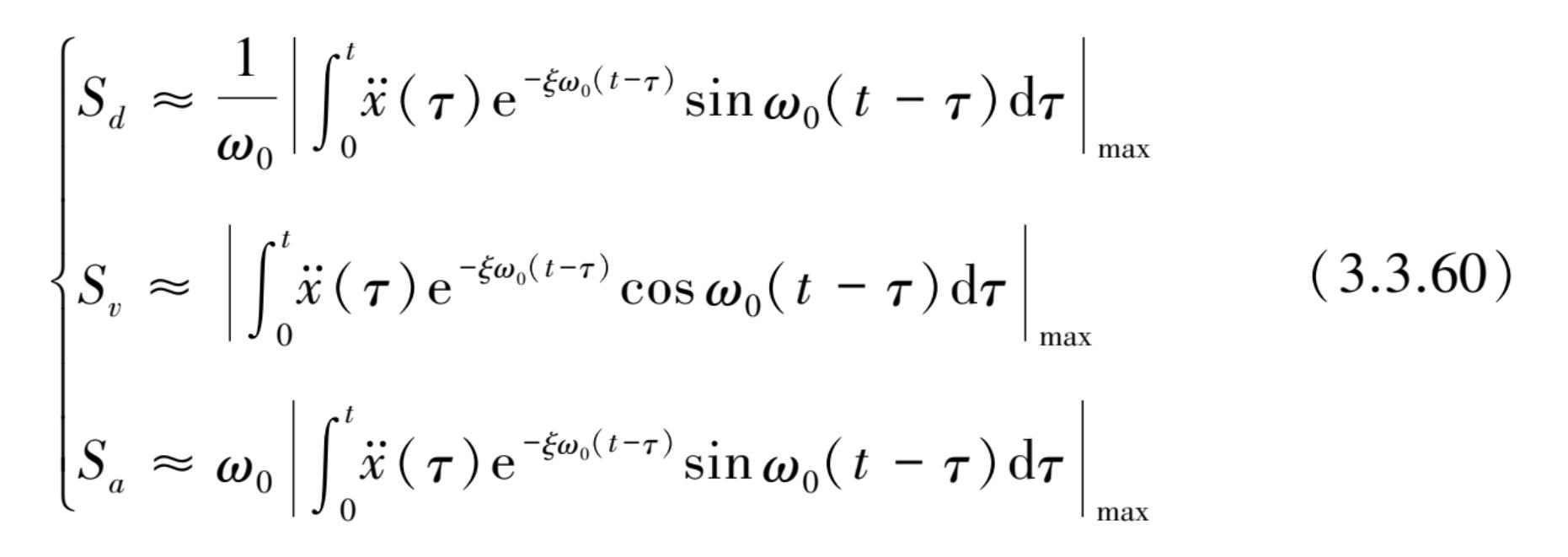
从上式 S d , S v 和 S a 之间关系可清楚看出它们之间存在简单关系式:
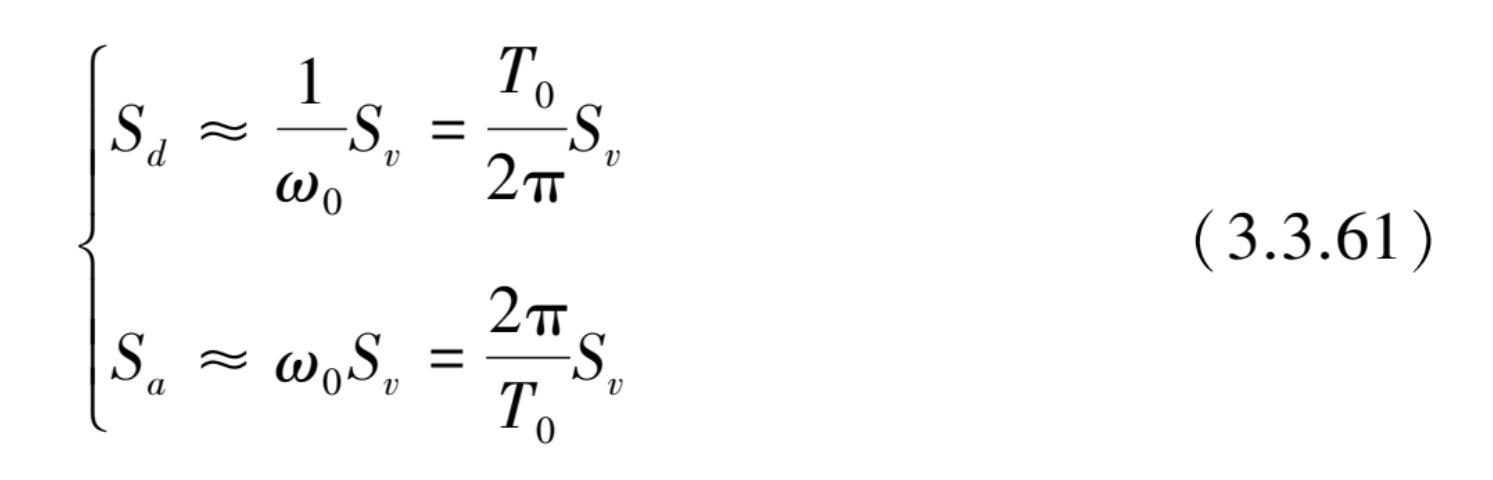
从式(3.3.61)可知,加速度反应谱与位移反应谱形状如图 3.3.8所示,分别为双曲线及通过原点有一定斜率的直线,分别称为拟加速度反应谱和拟位移反应谱。
3)标准反应谱表示方法
该表示方法采用加速度、速度和位移反应谱最大峰值
 ,
,
 和|
y
|
max
与基础输入
和|
y
|
max
与基础输入
 ,
,
 和|
x
|
max
之比来定义,为无量纲表示的地震动反应的放大倍数,并且也是阻尼比
ξ
、固有周期
T
0
或无阻尼固有频率
f
0
(
ω
0
)的函数。
和|
x
|
max
之比来定义,为无量纲表示的地震动反应的放大倍数,并且也是阻尼比
ξ
、固有周期
T
0
或无阻尼固有频率
f
0
(
ω
0
)的函数。
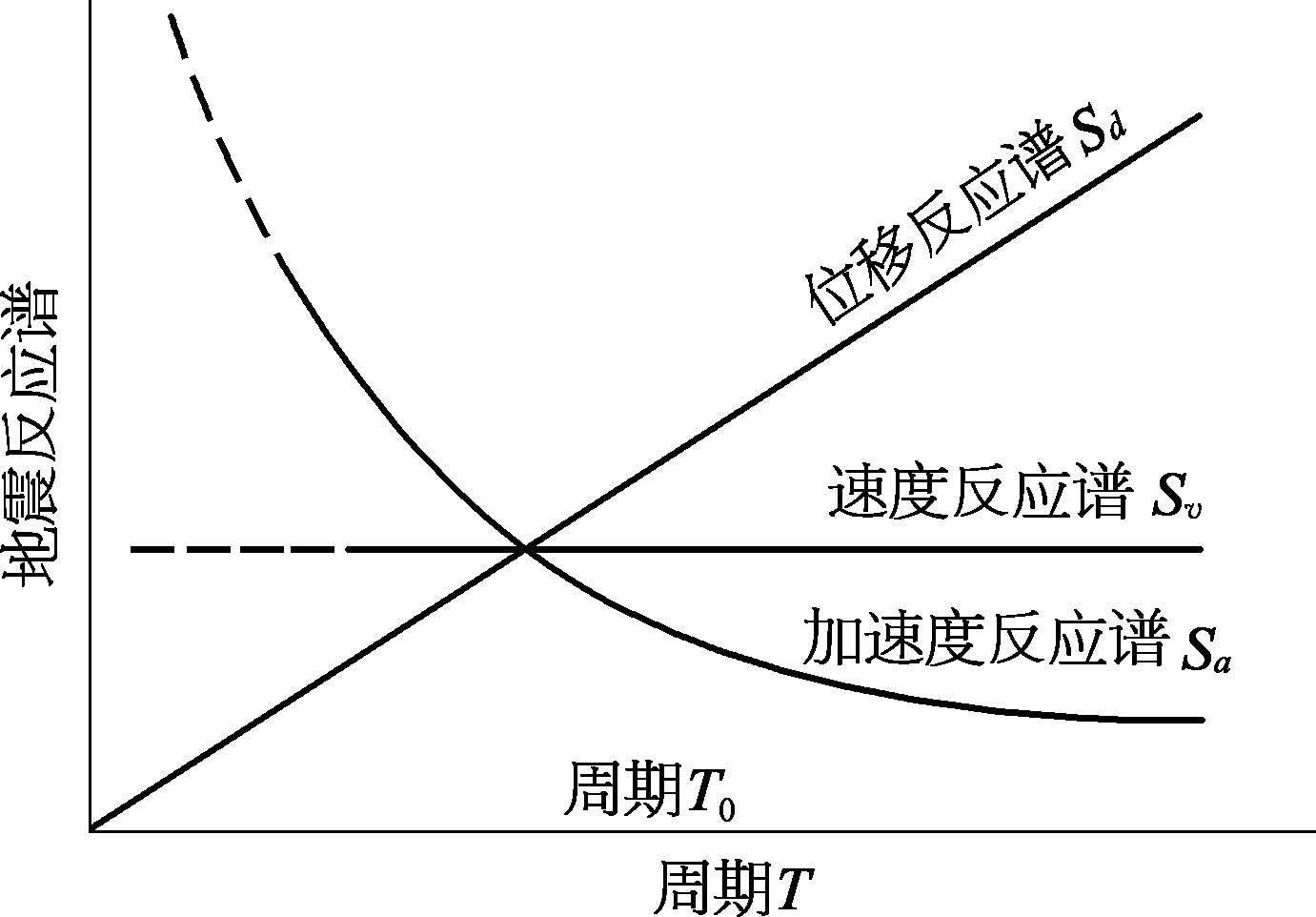
图3.3.8 拟反应谱表示方法
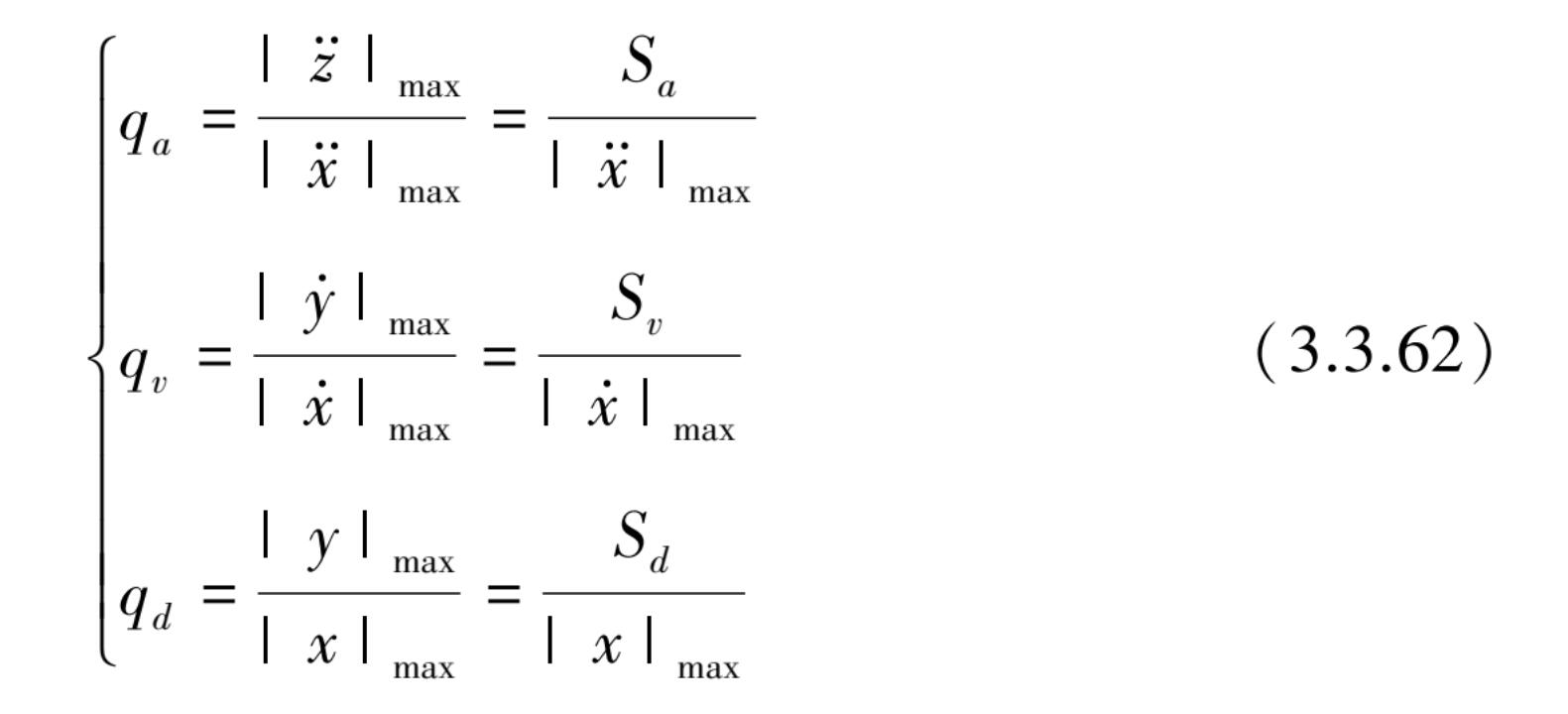
该无量纲 q a , q v 和 q d 分别称为标准加速度反应谱、标准速度反应谱和标准位移反应谱,统称为标准反应谱。该标准反应谱图的性质(见图 3.3.9)与反应谱图的形状(见图 3.3.6)完全相同,但它将纵坐标表示成一个无量纲的量。这在比较两个以上最大加速度值不同的地震反应特性时,标准反应谱是很有用的。
4)三重反应谱表示方法
由式(3.3.61)已知
 时,除以
时,除以
 得到近似值
得到近似值
 ,乘以
,乘以
 得到近似值
得到近似值
 。应用此简单关系式,在获得速度反应谱的同时可获得加速度反应谱
S
a
和位移反应谱的表示方法,并可描述在一张图内,这种图称为三重反应谱,如图 3.3.10 所示。
。应用此简单关系式,在获得速度反应谱的同时可获得加速度反应谱
S
a
和位移反应谱的表示方法,并可描述在一张图内,这种图称为三重反应谱,如图 3.3.10 所示。
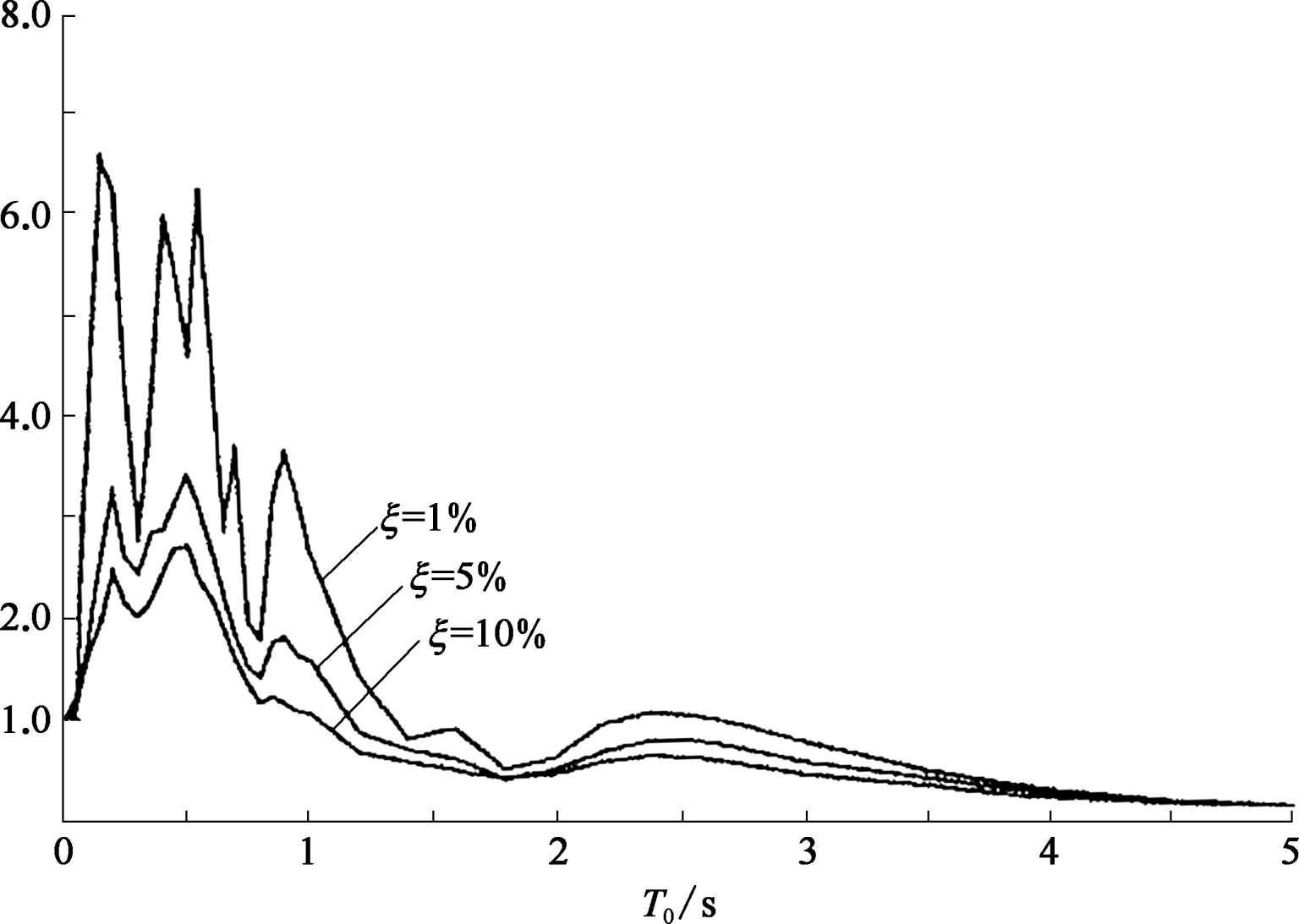
图3.3.9 标准加速度反应谱表示方法
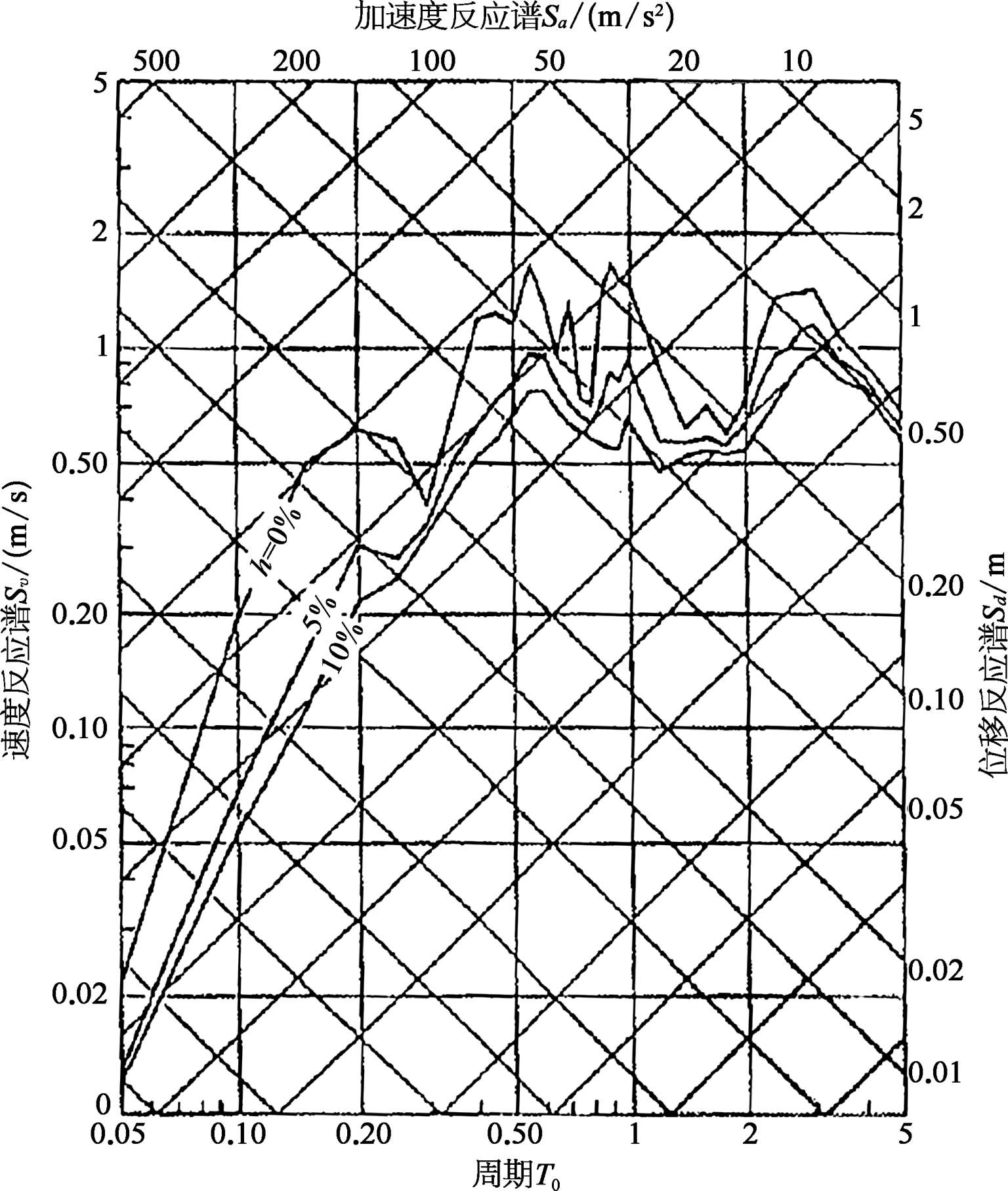
图3.3.10 三重反应谱表示方法
式(3.3.61)可改写为以 10 为对数坐标的表达式。
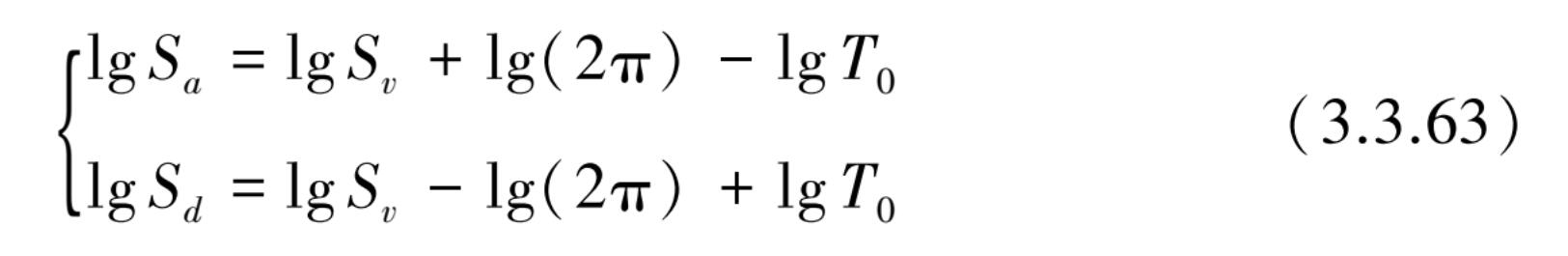
将图 3.3.10 的左边纵坐标 S v 和下面横坐标 T 0 均用对数刻度表示时,查对应 S a 为正斜率 45°直线对应上面横坐标的加速度值,查对应 S d 为斜率负45°直线对应右边纵坐标上的位移值。例如, S v =1 m/s, T 0 =0.5 s时,查正斜率对应的横坐标约为 1.25 m/s 2 加速度值,再查负斜率线对应右纵坐标线约为 0.08 m位移值。将 S v =1m/s代入式(3.3.63)得 S a =1.257 m/s 2 , S d =0.08 m,与表上查得的数据完全相符。这种三重反应谱表示方法确实很巧妙。
5)设计反应谱表示方法
在核电厂构筑物抗震设计时,为了计及构筑物和土壤材料特性中可能出现不确定因素对构筑物频率变化的影响,以及抗震分析中建模技术的近似性的影响,初始计算出来的反应谱通常要加以平滑修整,同时拓宽与构筑物固有频率有关的峰值。当证明采用分析法计算固有频率有效时,用拓宽的楼面设计反应谱进行设备或管系的抗震分析可通过如下方法实现反应谱峰值的拓宽,考虑在反应谱区间内有 N 个谱加速度峰,拓宽可按下式进行:
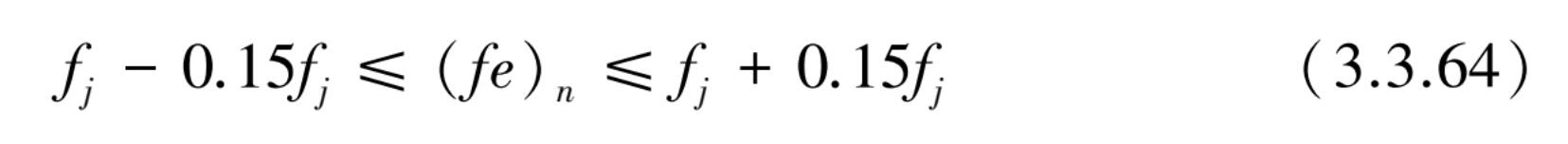
式中, f j 为反应谱上未拓宽谱中加速度谱峰所对应的频率值( n =1,…, N )。
式(3.3.64)表示了反应谱峰值处对应的频率 f j ,其拓宽频率为

经拓宽后的楼面反应谱称为设计楼面反应谱(见图 3.3.11),该设计楼面反应谱可正式作为SSC抗震分析的输入之用。
核电厂以基岩或土壤为基础的厂址,其安全停堆地震(SSE)或运行基准地震(OBE)地面设计反应谱的水平分量和垂直分量如图 3.3.12 所示。
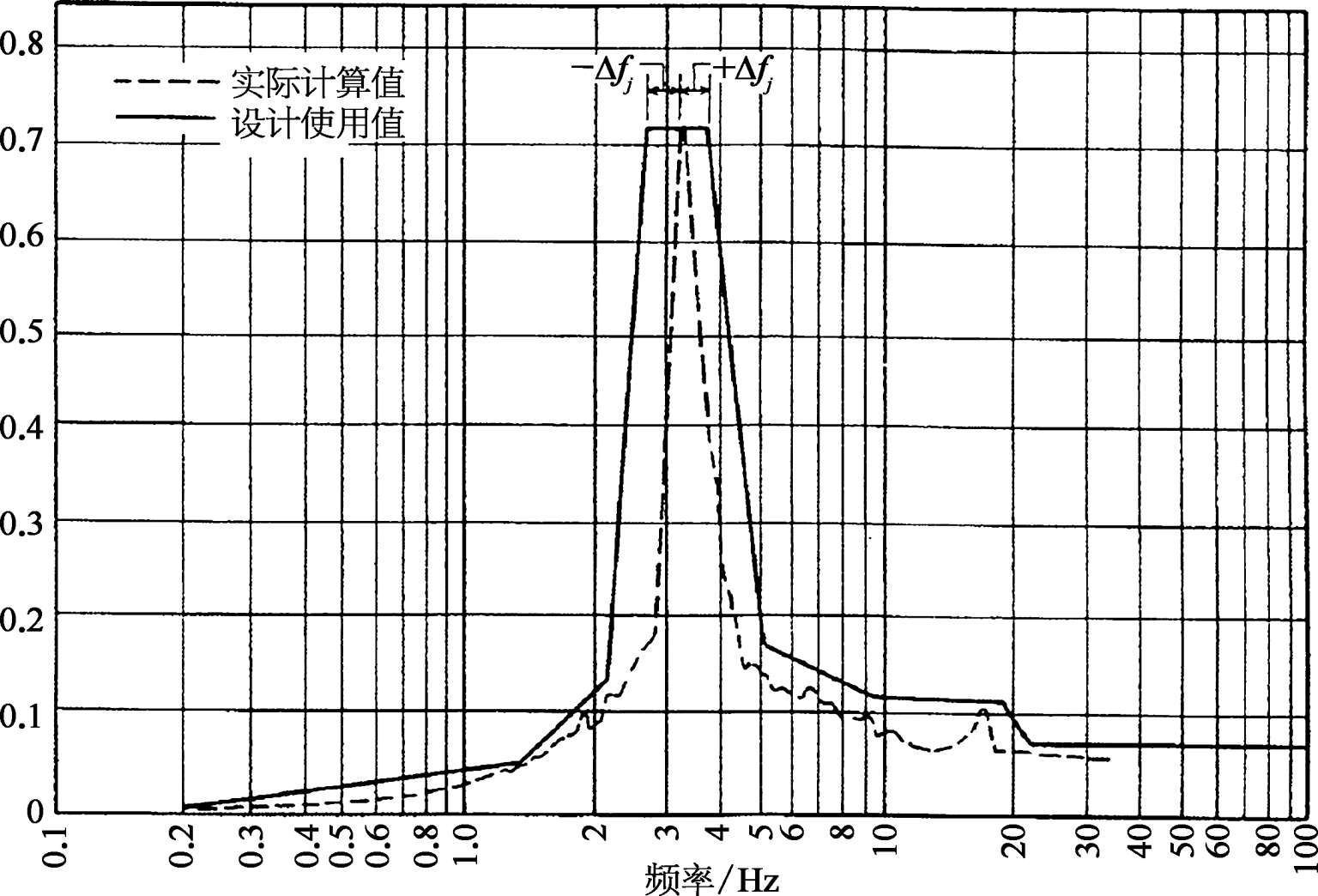
图3.3.11 反应谱峰值的拓宽
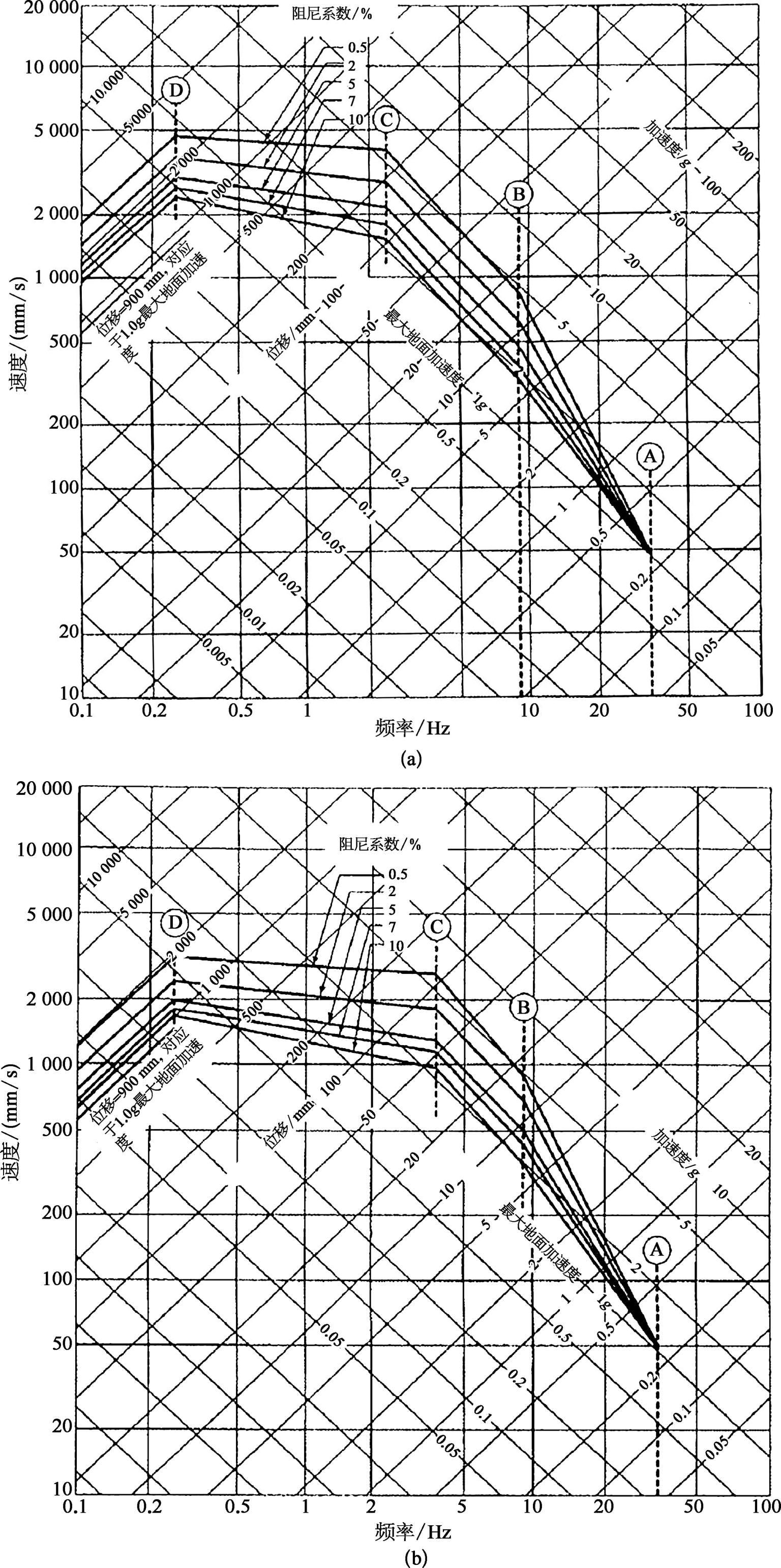
图3.3.12 换算到 1 g 水平地面加速度的设计反应谱
(a)水平方向;(b)垂直方向
图 3.3.12 为核电厂厂址输入的设计地面反应谱,它是按上述第 4 种三重反应谱表示方法与第 3 种标准反应谱表示方法结合在一起的表示方法。图中反应谱值对应于最大水平地面加速度 1.0 g 与所对应最大水平地面位移 915 mm(36 in)的时程输入,所选厂址的地震反应谱值可按所选厂址地震规定的最大水平地面加速度按比例进行线性换算。
对应于图 3.3.12 (a)和(b)设计反应谱上控制点的谱放大系数在表 3.3.1 和表 3.3.2 中列出。其之间的阻尼比所对应的反应值可按线性插值方法求出。
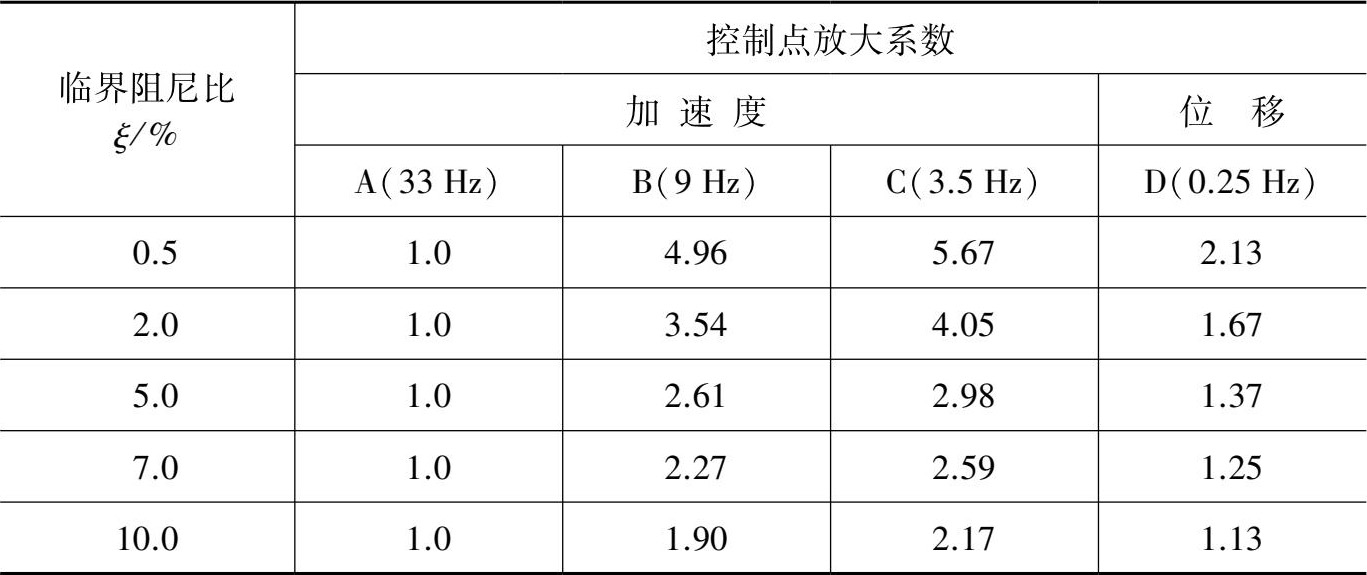
表3.3.1 水平设计反应谱控制点谱放大系数对应值
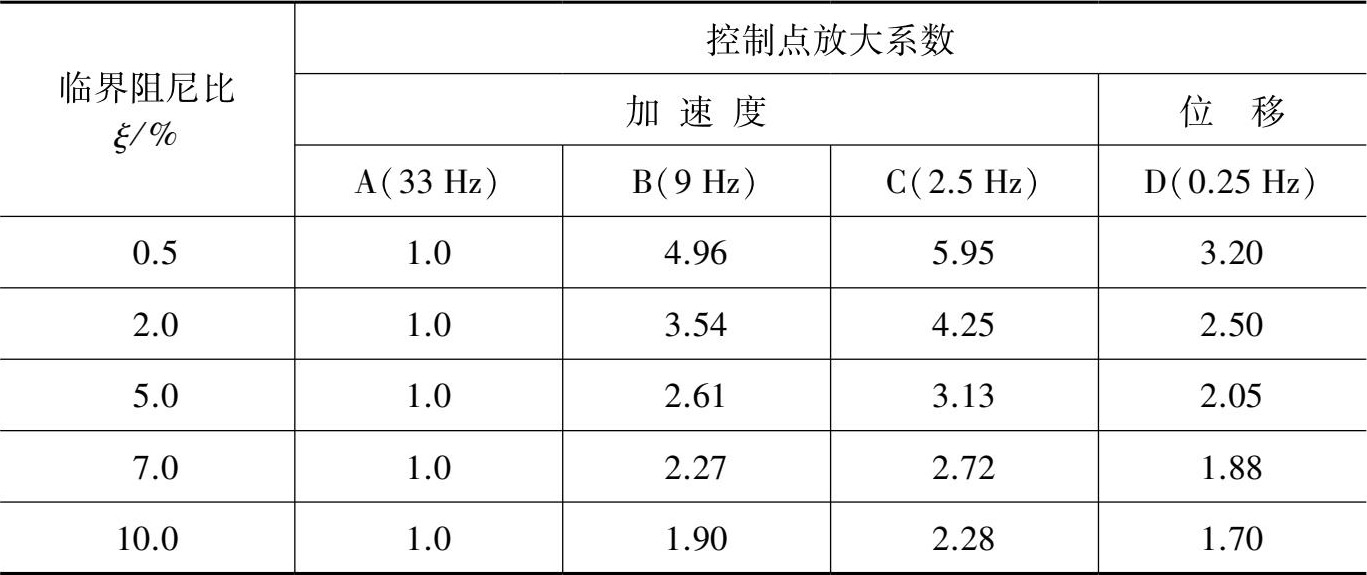
表3.3.2 垂直设计反应谱控制点谱放大系数对应值