




振动物体的黏性阻尼认为其运动受到的阻力近似地假定为与物体运动速度成正比,类似于物体沿润滑表面运动或在流体中低速运动所承受的阻力,其他各种阻尼对振动的影响可以简化为黏性阻尼来计及,在工程上近似应用也能获得有用的结果。
图 3.2.1 是质量为
m
、刚度为
k
和阻尼为
c
的振动系统,
z
(
t
)为质量
m
的绝对位移,质量运动惯性力
 与弹性恢复力
kz
、黏性阻尼力
与弹性恢复力
kz
、黏性阻尼力
 相平衡,其运动方程为
相平衡,其运动方程为
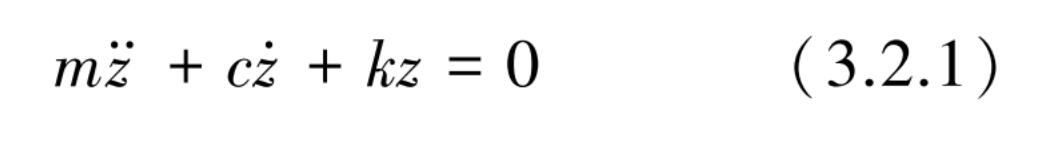
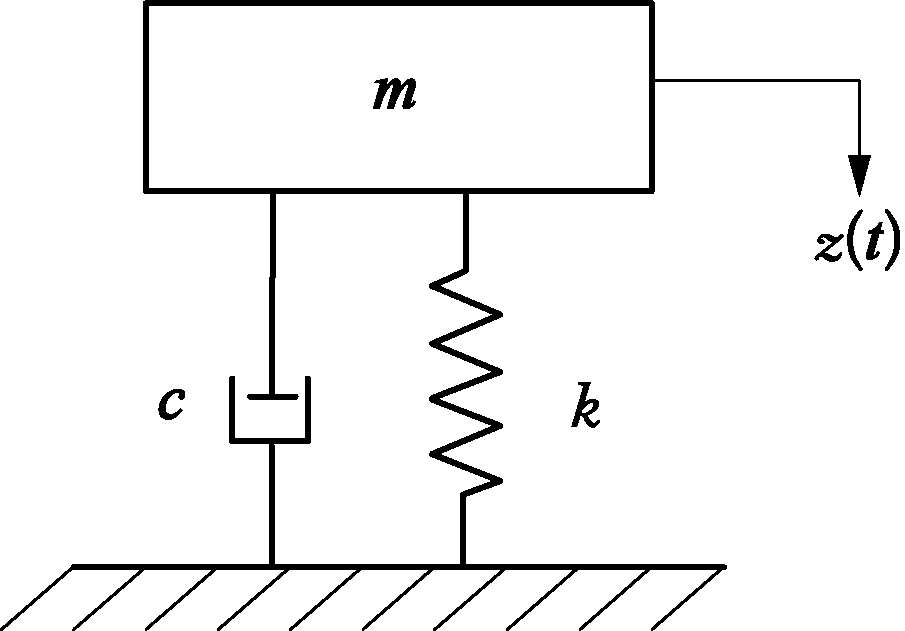
图3.2.1 黏性阻尼振动系统
引入无量纲阻尼比 ξ 与无阻尼固有频率 ω ,式(3.2.1)可转化为
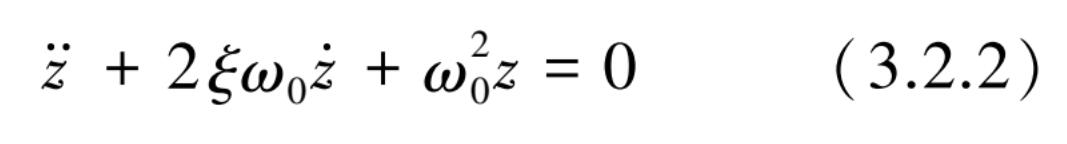
式中,
 为无阻尼固有频率,
为无阻尼固有频率,
 =
=
 ;
ξ
为阻尼比,
ξ
=
;
ξ
为阻尼比,
ξ
=
 =
=
 ;
;
 为临界阻尼系数,
为临界阻尼系数,
 =
=
 =
=
 。
。
为求式(3.2.2)的通解,设: z =e st 代入式(3.2.2)得到的特征方程为

其特征方程的两个根为
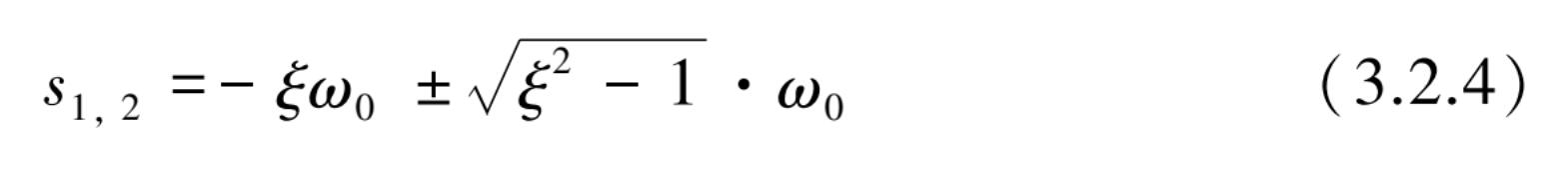
方程的通解为

式中, A , B 为待定常数。
从式(3.2.5)可以证明,当阻尼比 ξ ≥ 1 时,系统不能出现振动,只有 ξ <1 时,即在小阻尼条件下,系统才存在衰减振动。
当 ξ >1 时,由式(3.2.4)可知, s 1 和 s 2 是不相等的负实数,代入方程式(3.2.5)可得
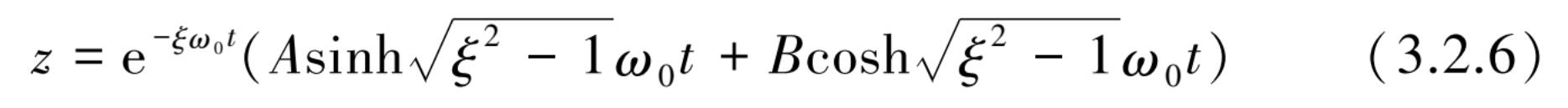
式中,
A
,
B
为待定常数,由初始条件
t
=0,
z
=
z
0
和
z
=
 确定可得
确定可得
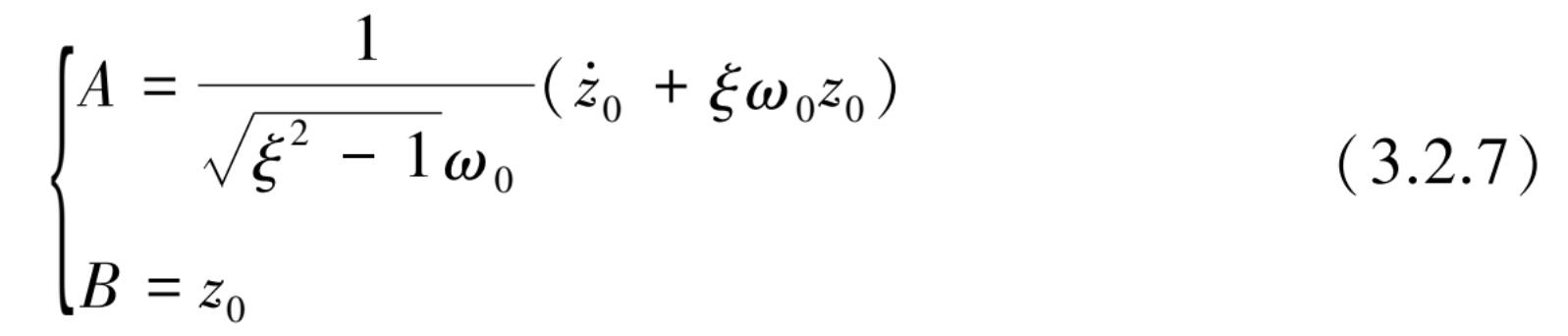
代入式(3.2.6)后得
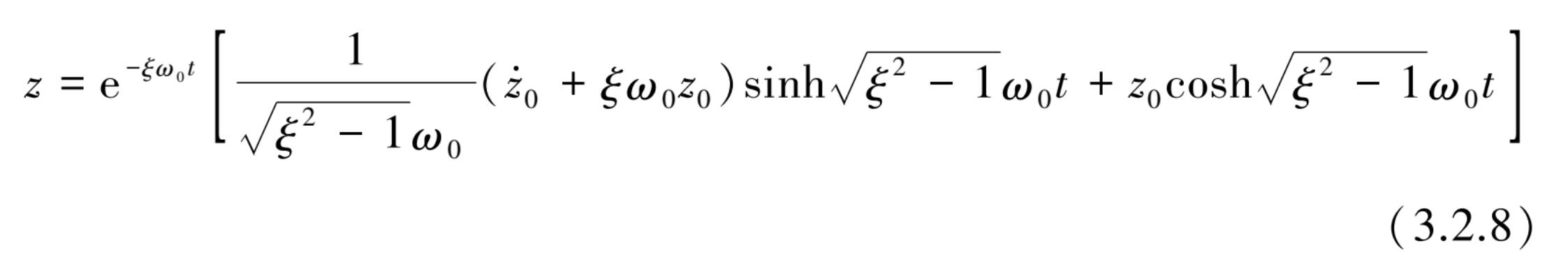
位移
z
(
t
)随时间变化曲线如图 3.2.2 所示,由图可知,不管初始速度
 >0,
>0,
 =0 还是
=0 还是
 <0 条件下,当
z
(
t
)离开
t
=0 初始位移
z
0
平衡位置以后,中间最多振荡一次并最终趋向至零。在这种
ξ
>1 的大阻尼作用下,系统运动将不会产生反复振动。
<0 条件下,当
z
(
t
)离开
t
=0 初始位移
z
0
平衡位置以后,中间最多振荡一次并最终趋向至零。在这种
ξ
>1 的大阻尼作用下,系统运动将不会产生反复振动。
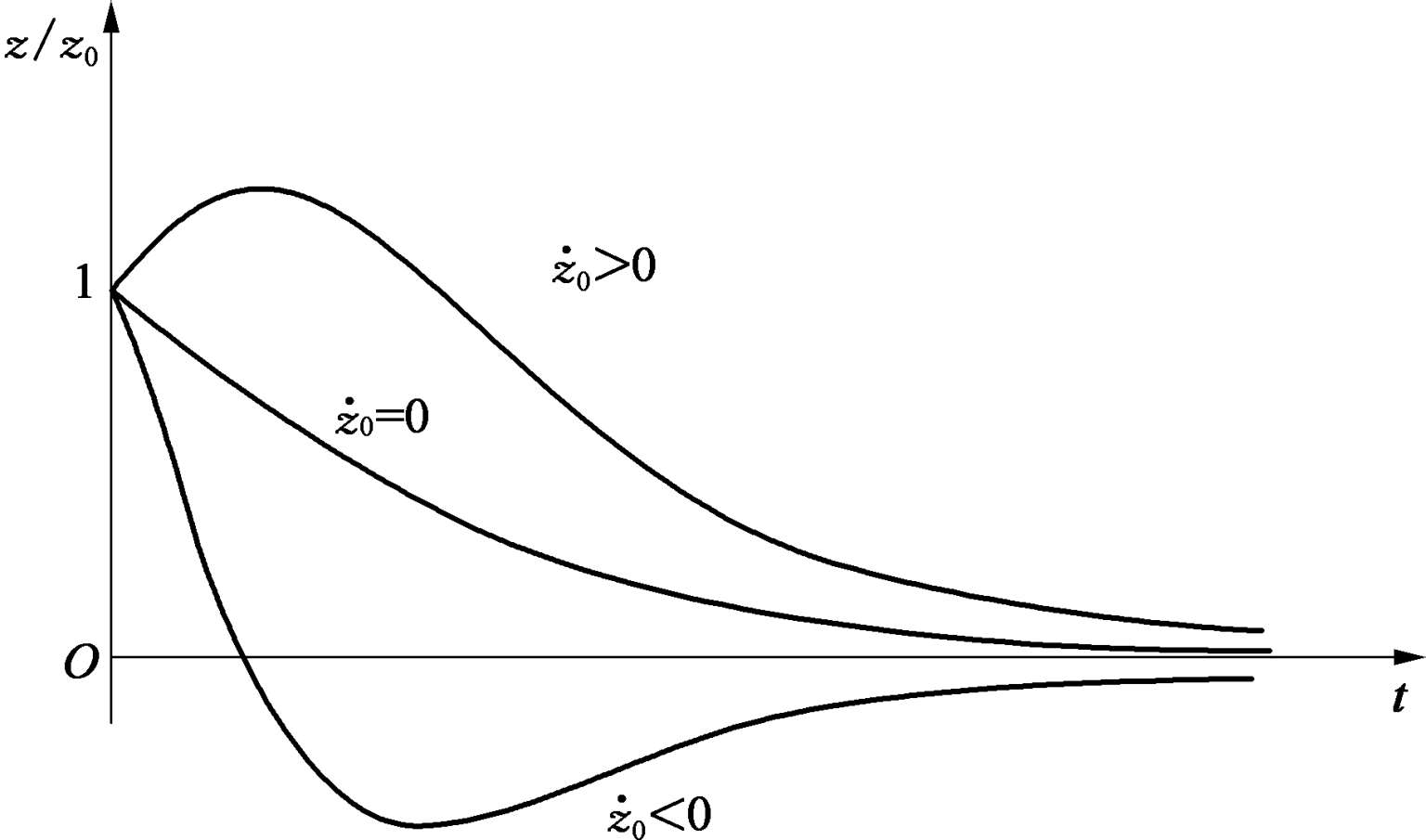
图3.2.2 大阻尼下的 z ( t )反应曲线
当 ξ =1 时,即阻尼等于临界阻尼 c = c c 情况下,式(3.2.3)可知其代数方程为重根 s 1,2 =- ω 0 ,为此方程的通解为

同理,积分常数
A
,
B
由初始条件
t
=0,
z
=
z
0
和
 =
=
 0
确定,可得
0
确定,可得
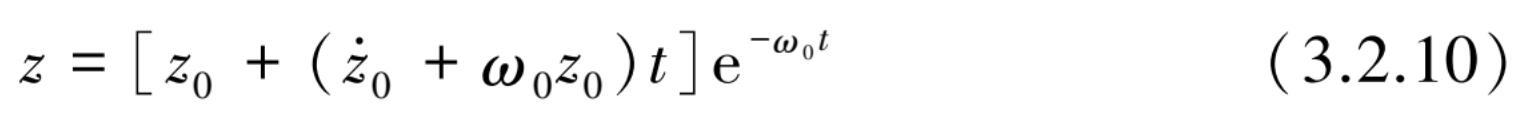
由此可知,该系统的运动仍属于非周期的衰减曲线。图 3.2.3 展示了初始速度
 0
>0,
0
>0,
 0
=0 或
0
=0 或
 0
<0 条件下,当
z
(
t
)离开
t
=0 初始位移
z
0
平衡位置之后,其间最多振荡一次最终衰减到零位。
0
<0 条件下,当
z
(
t
)离开
t
=0 初始位移
z
0
平衡位置之后,其间最多振荡一次最终衰减到零位。
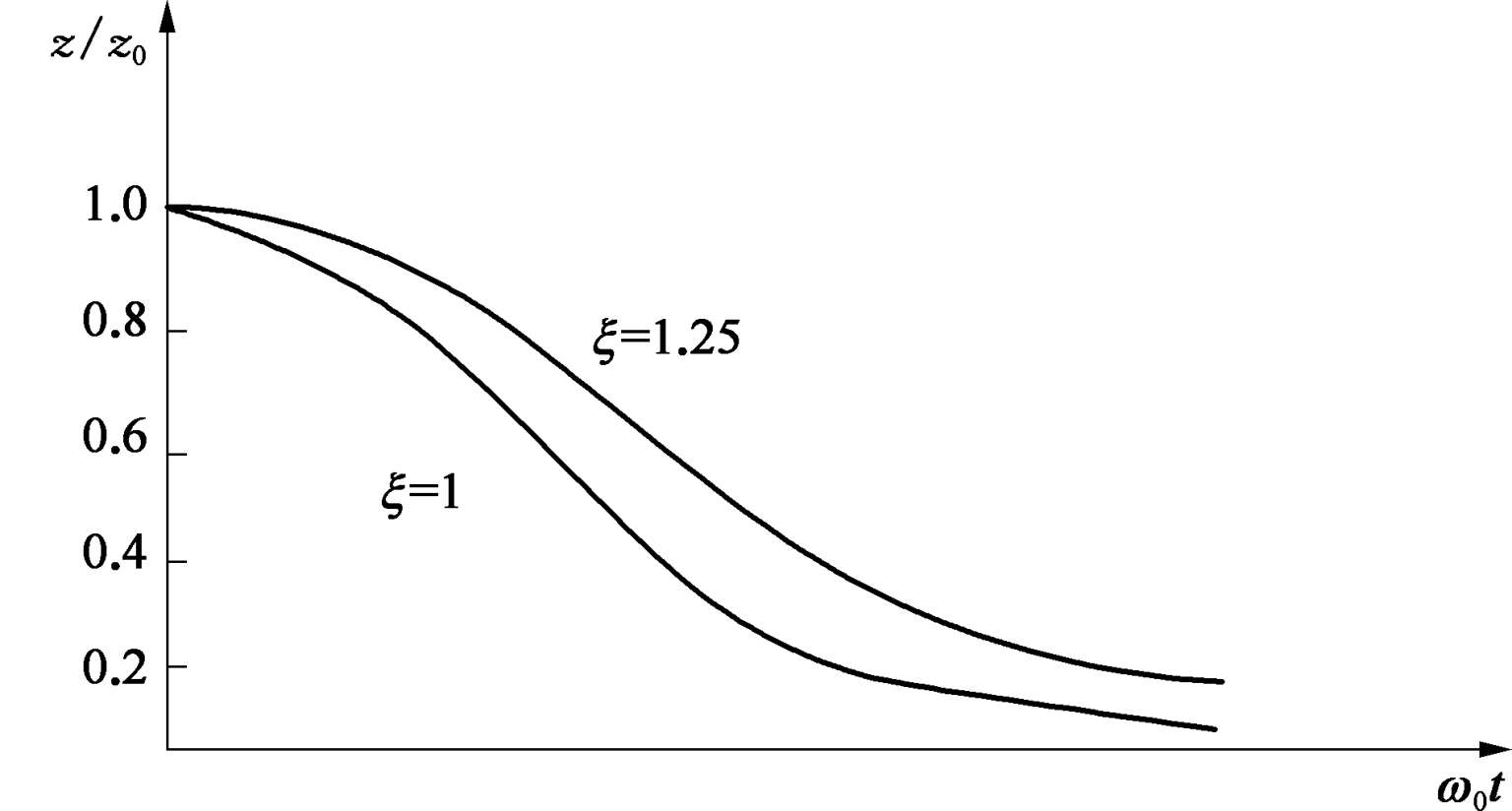
图3.2.3 临界阻尼 z ( t )反应曲线
当 ξ <1 时,即小阻尼条件下,很容易求解方程(3.2.3)的两个根为
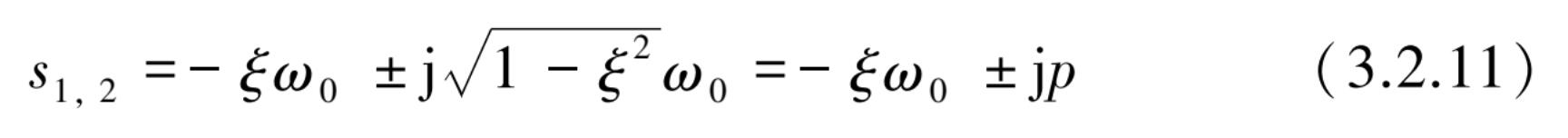
式中,
p
=
 为系统的共振频率。
为系统的共振频率。
式(3.2.2)位移和速度的解为
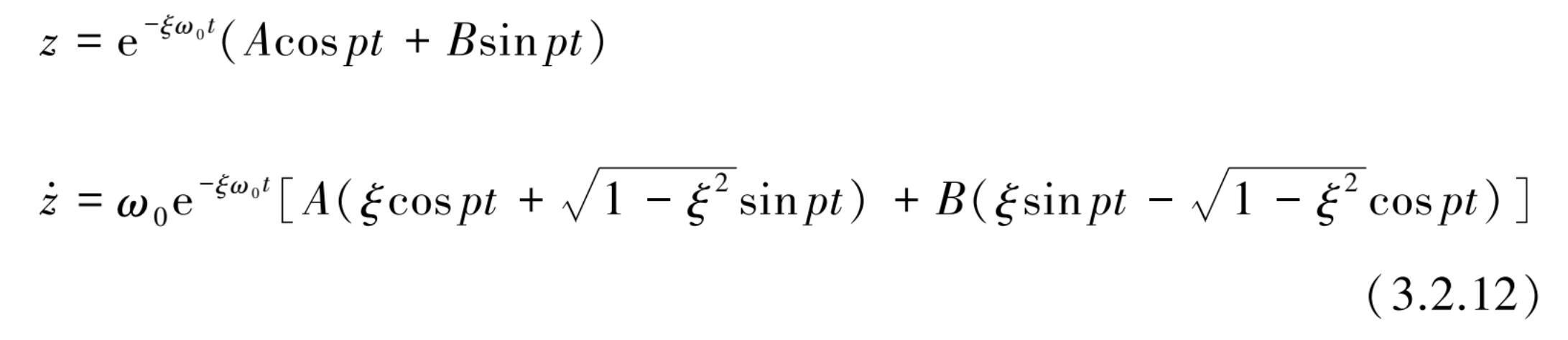
A
,
B
为积分常数,可由初始条件
t
=0 时
z
=
z
0
和
 =
=
 0
代入式(3.2.12)后求得。
0
代入式(3.2.12)后求得。

则通解为
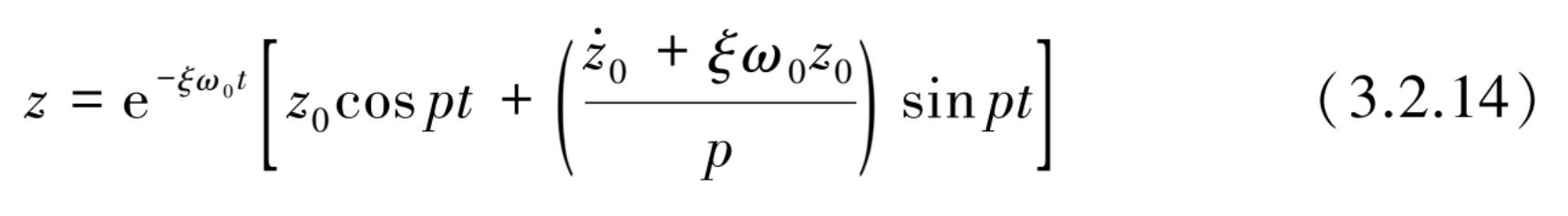
通解式(3.2.14)通常有下列两种表示形式。
(1)由初始条件直接表示。
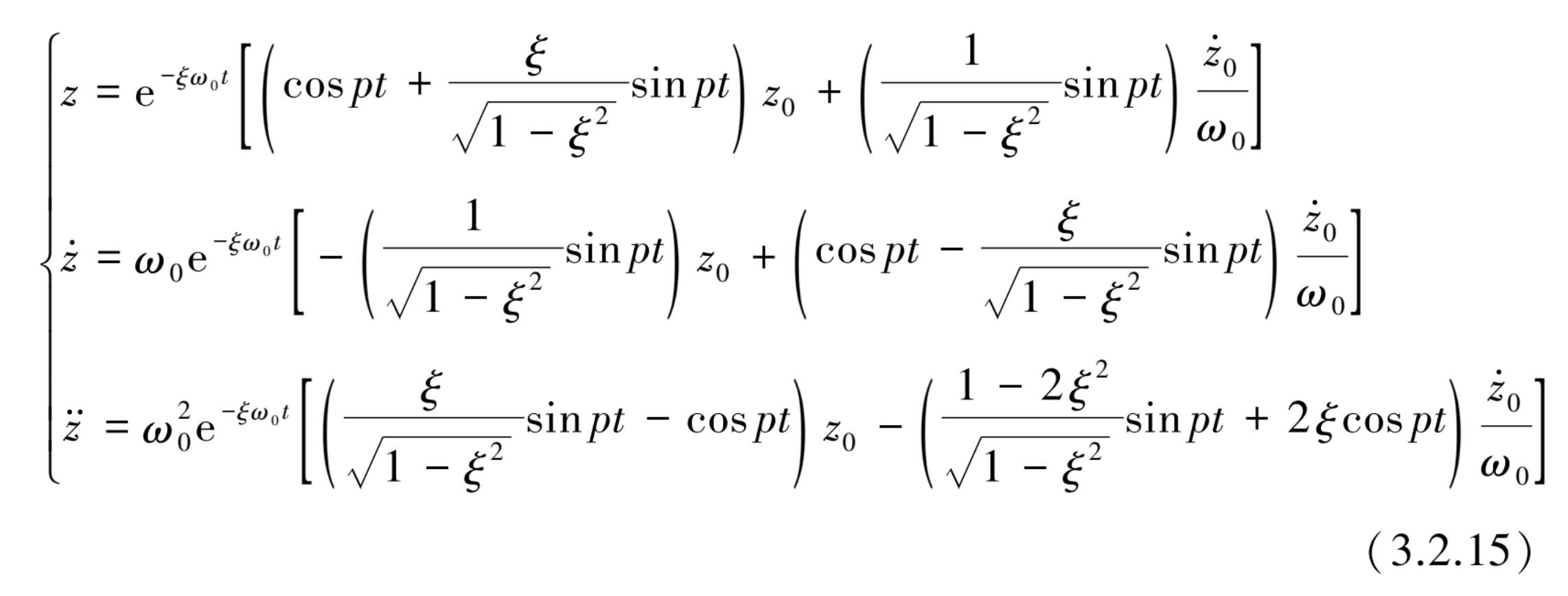
(2)由更简洁的方法表示。
在式(3.2.12)中常数
A
和
B
由幅值
C
和相位角
 来替代。
来替代。
设幅值

相位
 =
=
 =
=

 =
=
 =
=

代入式(3.2.14)得到 z 的简易表达式为

由此对式(3.2.16)求导后可求得速度为
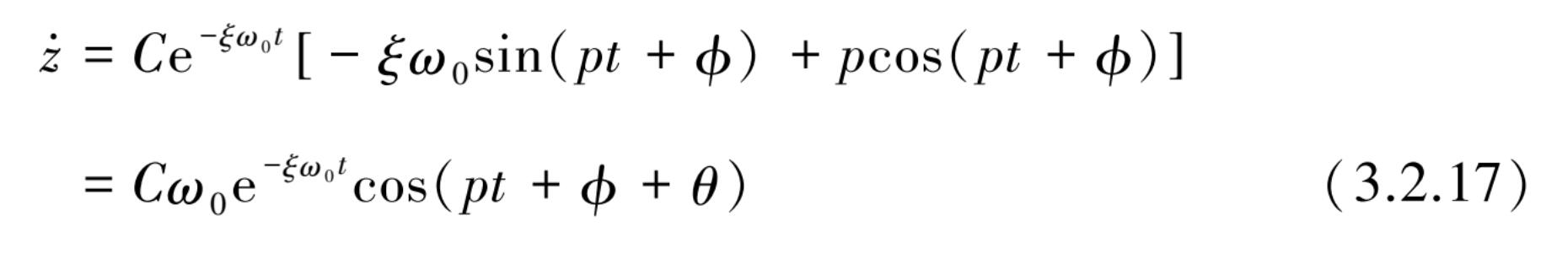
设:
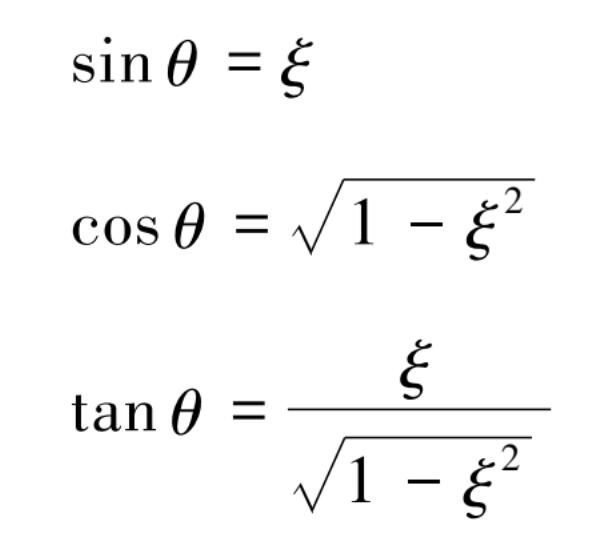
加速度可由式(3.2.2)直接求得
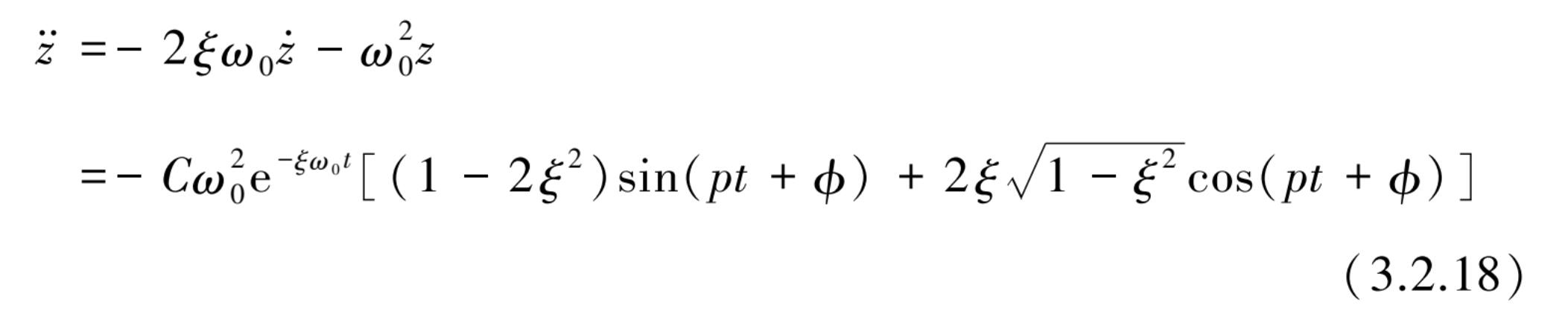
设:
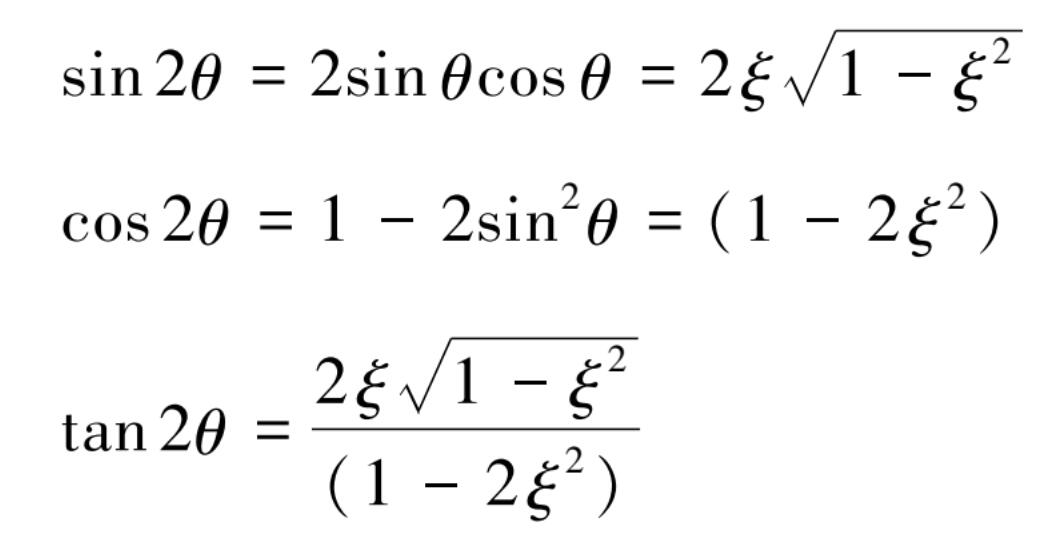
代入式(3.2.18)整理得
 =
=
 sin(
pt
+
sin(
pt
+
 +2
θ
)
+2
θ
)
式中,
p
=
 。
。
将位移、速度与加速度汇总得
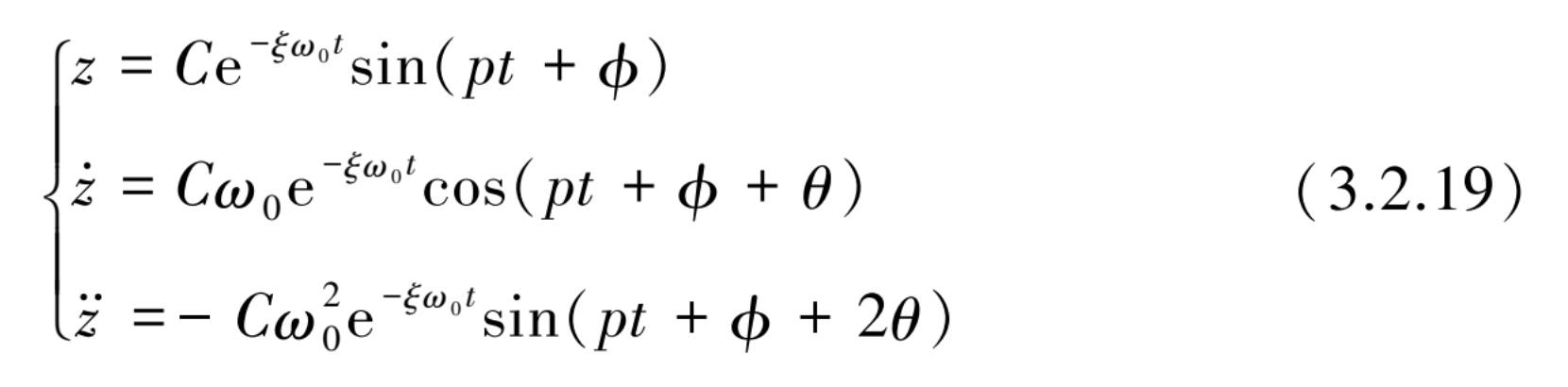
从以上两种不同表达形式的解可清楚地看出,该系统的运动属于小阻尼作用下的振动,其振动频率
p
=
 小于系统无阻尼下的固有频率
ω
0
。对于何种初始条件下,系统的位移、速度与加速度幅值随时间变化均按指数形式衰减,最终趋向零位(见图 3.2.4)。
小于系统无阻尼下的固有频率
ω
0
。对于何种初始条件下,系统的位移、速度与加速度幅值随时间变化均按指数形式衰减,最终趋向零位(见图 3.2.4)。
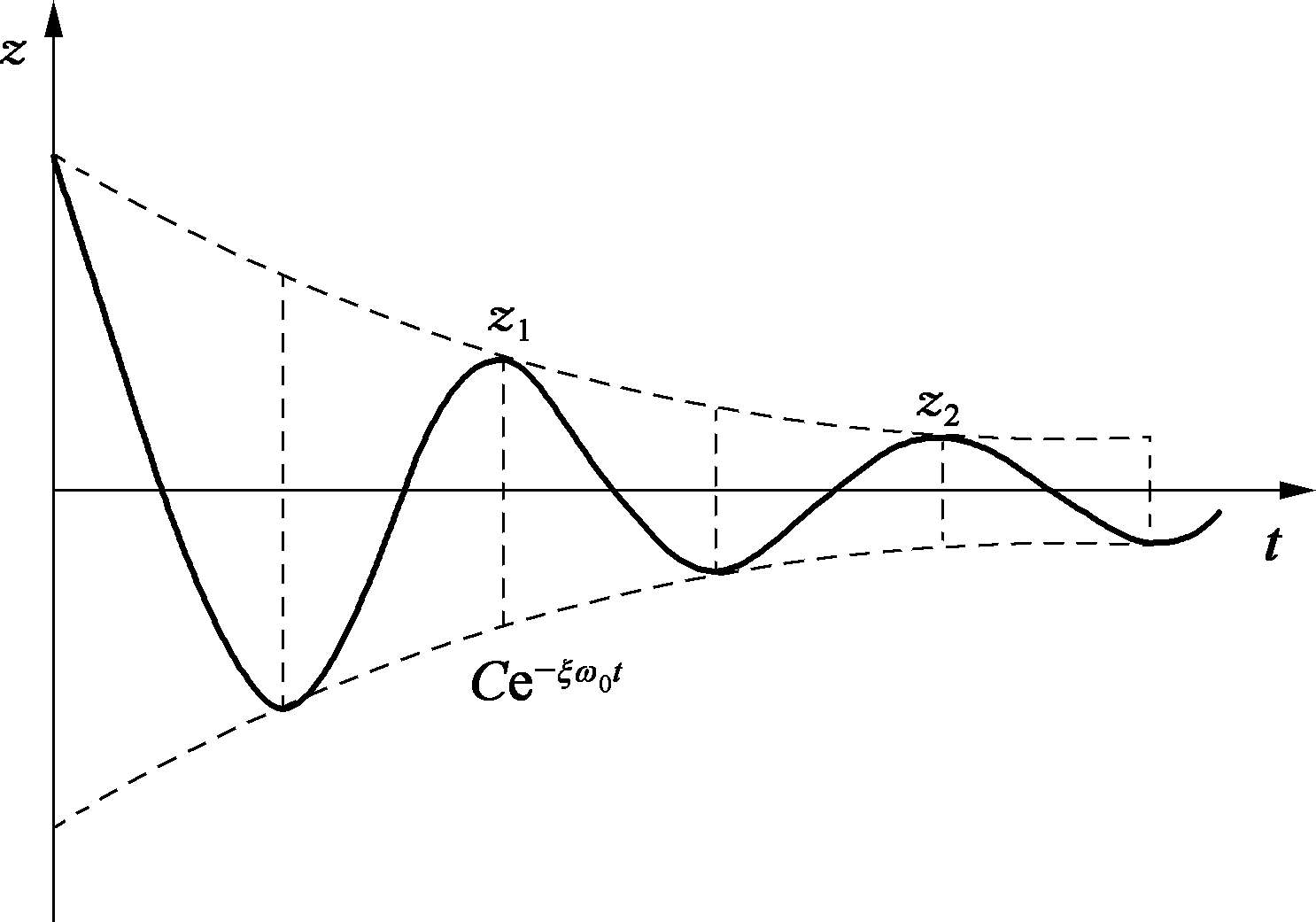
图3.2.4 小阻尼下的对数衰减曲线
从图 3.2.4 可明显观察到,在对数衰减曲线上任意相邻两次振动的振幅 z 1 和 z 2 之比为
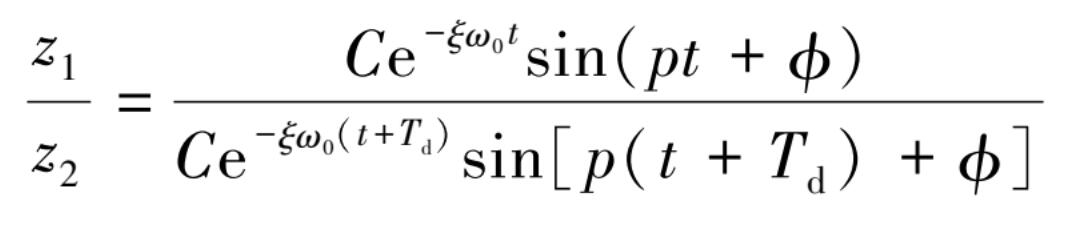
由于正弦函数满足周期性质,故上式简化为
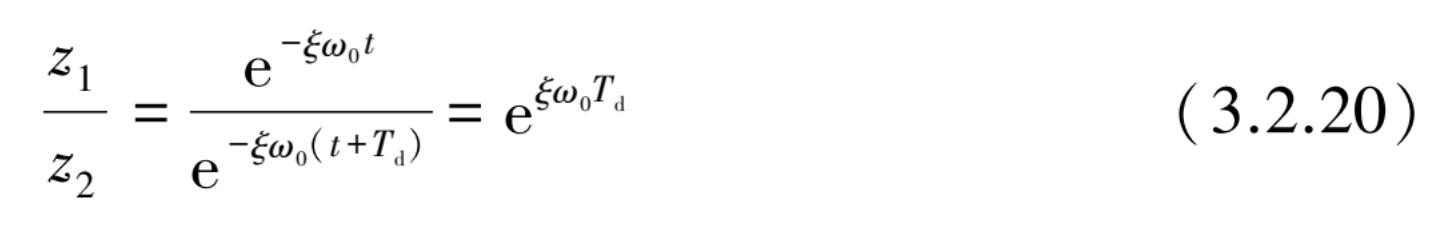
该比值取e为底的对数后称为“对数衰减率”,即
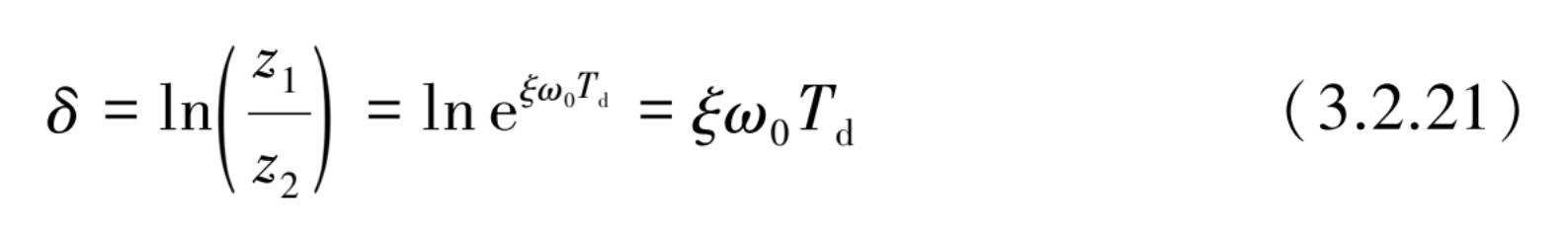
式中,衰减振动的周期 T d 为
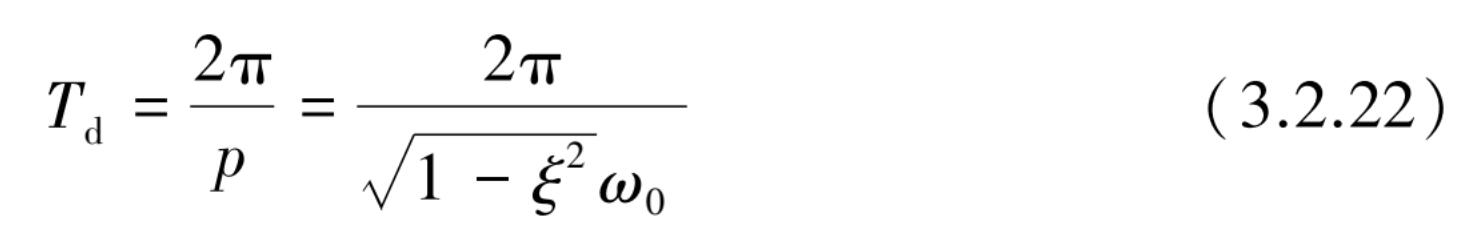
将 T d 代入式(3.2.21)后得对数衰减率为

当
ξ
 1 时,近似为
1 时,近似为

在对数衰减率曲线上有连续 n 次振动时,振幅 z 1 , z 2 , z 3 ,…, z n 有如下关系:
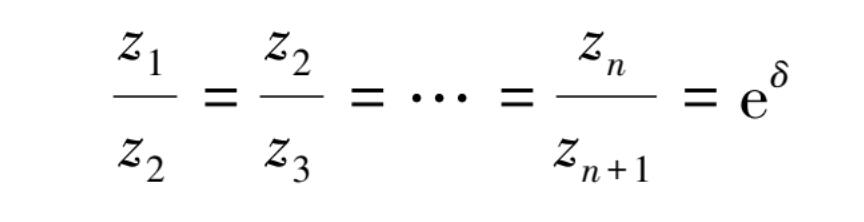
则
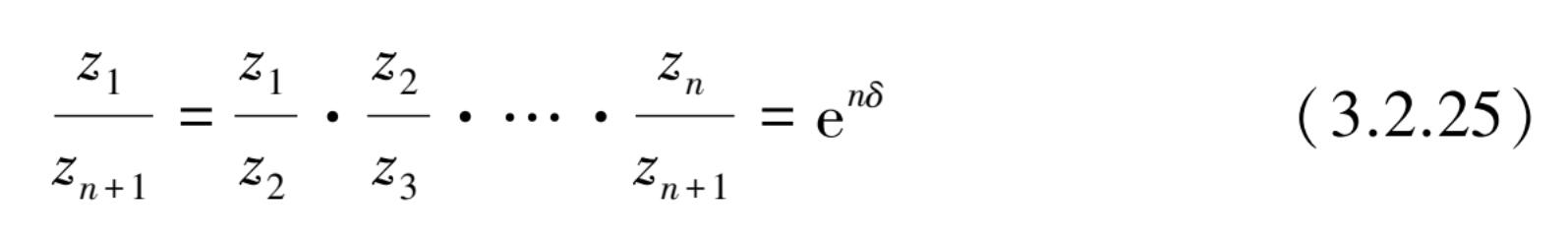
两端取对数得

式(3.2.26)表示,小阻尼下,只要测量衰减振动中的第 1 次和第 n +1 次的振幅之比,即可估计出对数衰减率,从而按(3.2.24)确定阻尼比的大小。
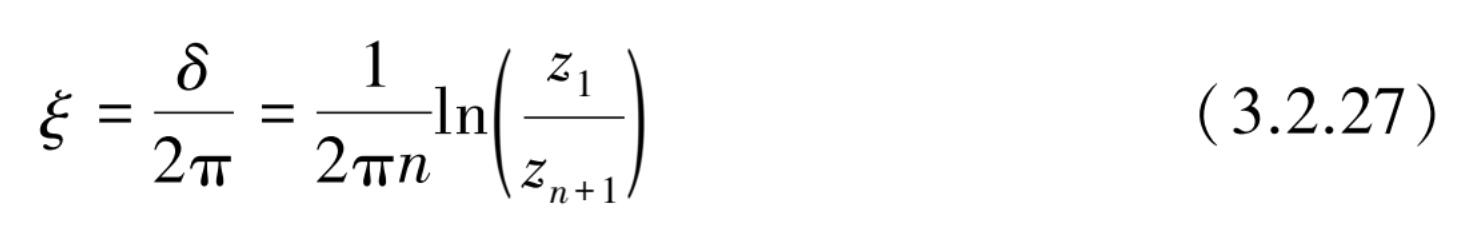
[例 1]
已知:
m
=9.8 kg,
k
= 25 ×980 N/ m,
c
=0.1 ×980 N·s/ m。当初始振幅和速度分别为
z
0
=10 mm,
 =0 时,求:对数衰减率
δ
,并估计使振幅衰减至初始值的 1%所需要的振动次数和时间。
=0 时,求:对数衰减率
δ
,并估计使振幅衰减至初始值的 1%所需要的振动次数和时间。
解:
无阻尼固有圆频率

阻尼比

求得振动衰减率 δ ≈ 2π ξ =0.628
设在振动 n 次后,振幅衰减至原振幅的 1%,则
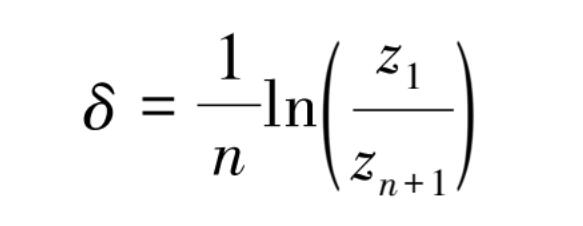
得到

所需的时间为
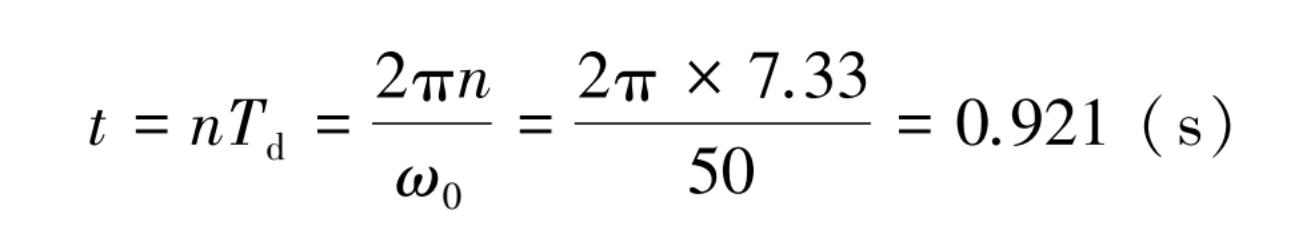
[例 2] 已知: m =150 kg, k = 32.14 kN/ m。求:
(1)系统的临界阻尼系数;(2)该系统的 c =0.685 kN·s/ m时,问经过多长时间振幅减至 10%;(3)衰减的周期是多少?
解:
(1)

c c =2 m ω 0 =2 ×150 ×14.64=4.39(kN·s/ m)
(2)
ξ
=
 =
=
 =0.156
=0.156
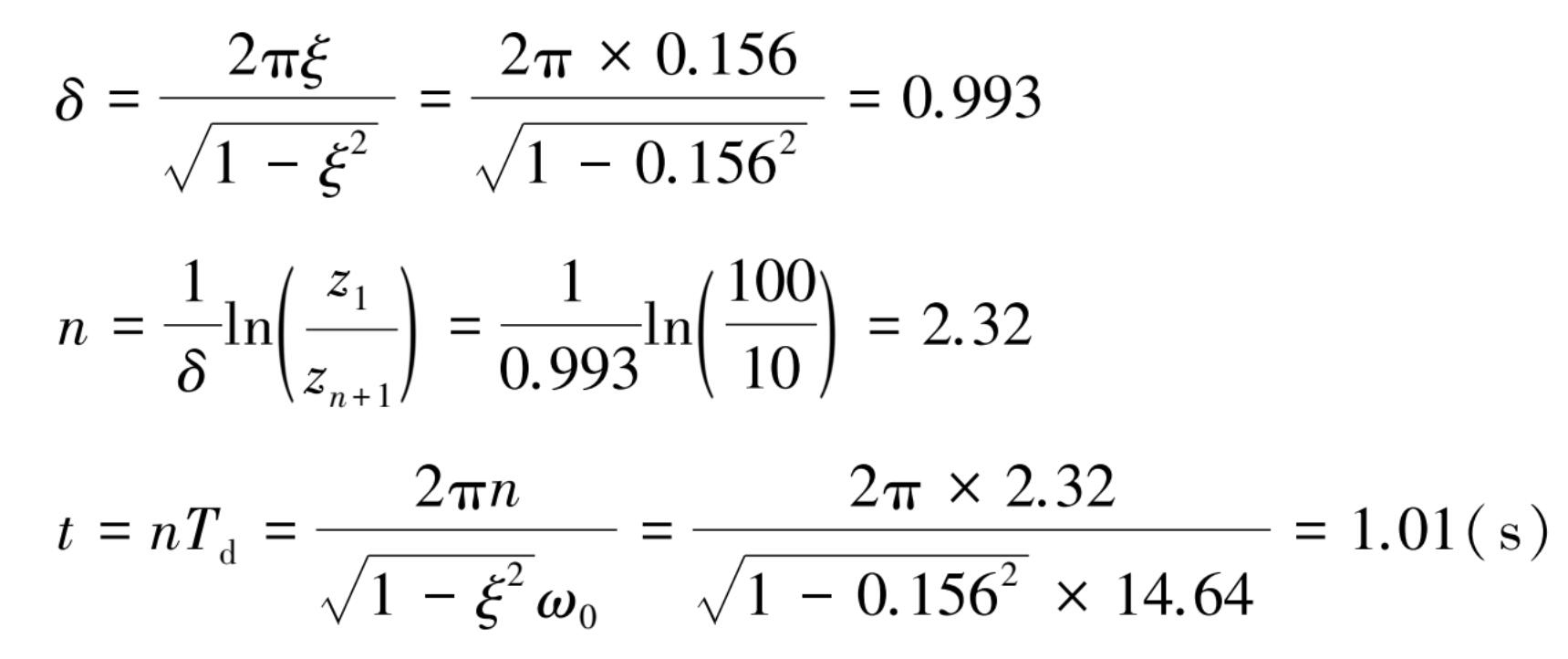
(3)
 =
=
 =
=
 =0.434(s)
=0.434(s)