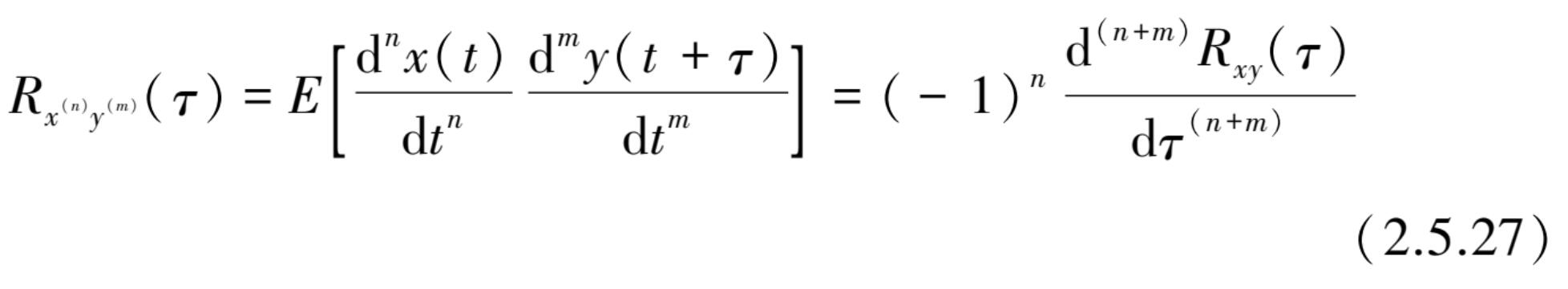表示两个随机过程 x ( t )和 y ( t )记录数据之间相关性的统计值称为互相关函数。
图 2.5.1 所示的 x ( t )在 t 时刻值与 y ( t )在( t + τ )时刻值之间的互相关函数可用观察时刻周期 T 上两个值的平均乘积得到其统计值。当 T 趋于无穷大时,平均乘积将趋于正确的“互相关函数”,即
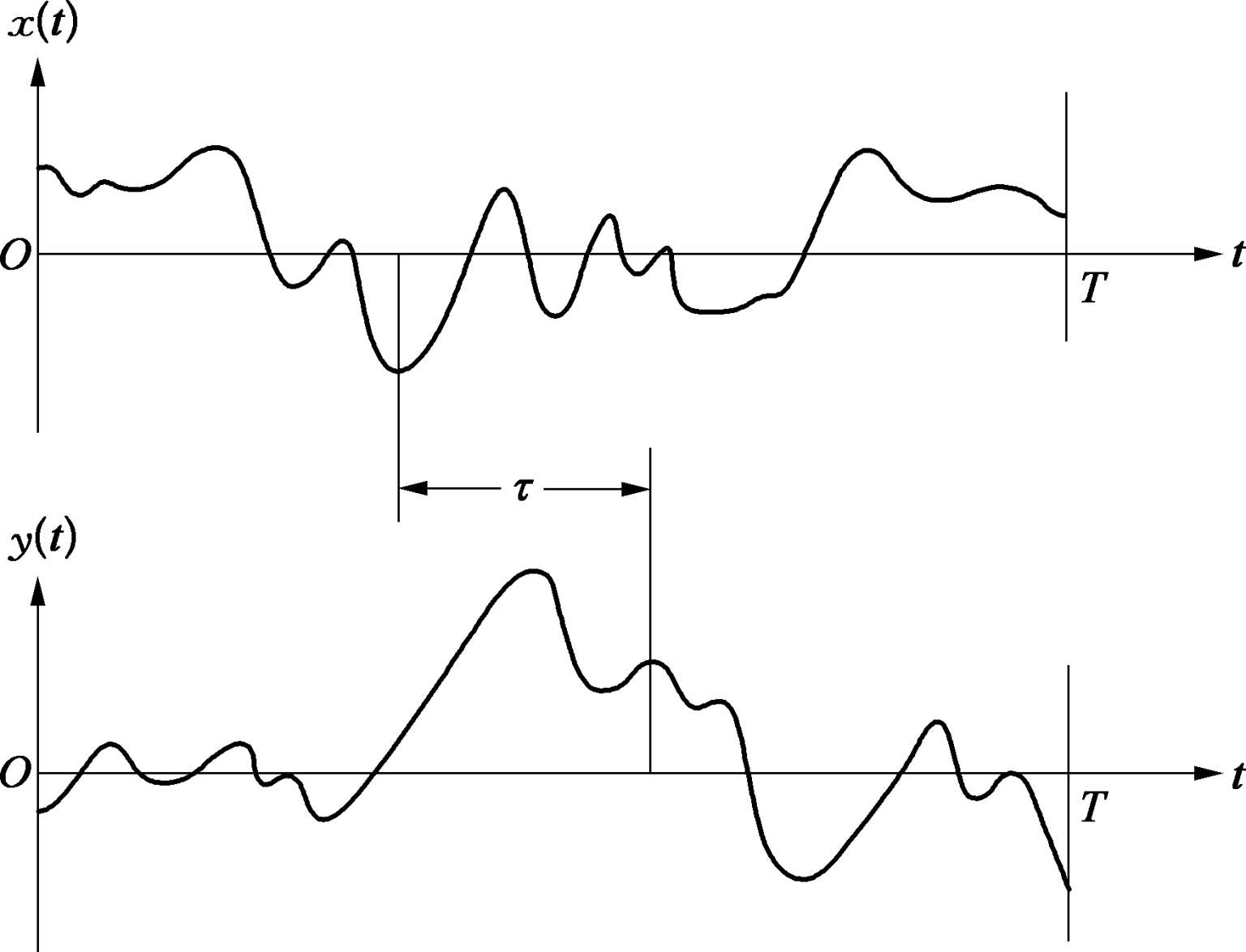
图2.5.1 互相关函数的测量
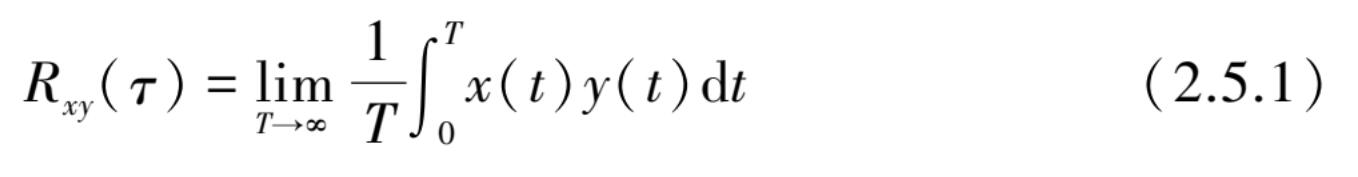
R xy ( τ )总是一个可正可负的实函数,当 x , y 互换时, R xy ( τ )是对称于纵坐标的,即满足:

如下两个不等式成立:

当 R xy ( τ )=0 时,称 x ( t )和 y ( t )不相关;当某时间位移 τ 上出现峰值时,则认为该时刻上的 x ( t )和 y ( t )具有强的相关性。如图 2.5.2 表明两个时间位移 τ 上有较高的相关特征。
对应均值 μ x = μ y =0 时,则可用相关函数系数 ρ xy ( τ )来表示互相关特性:
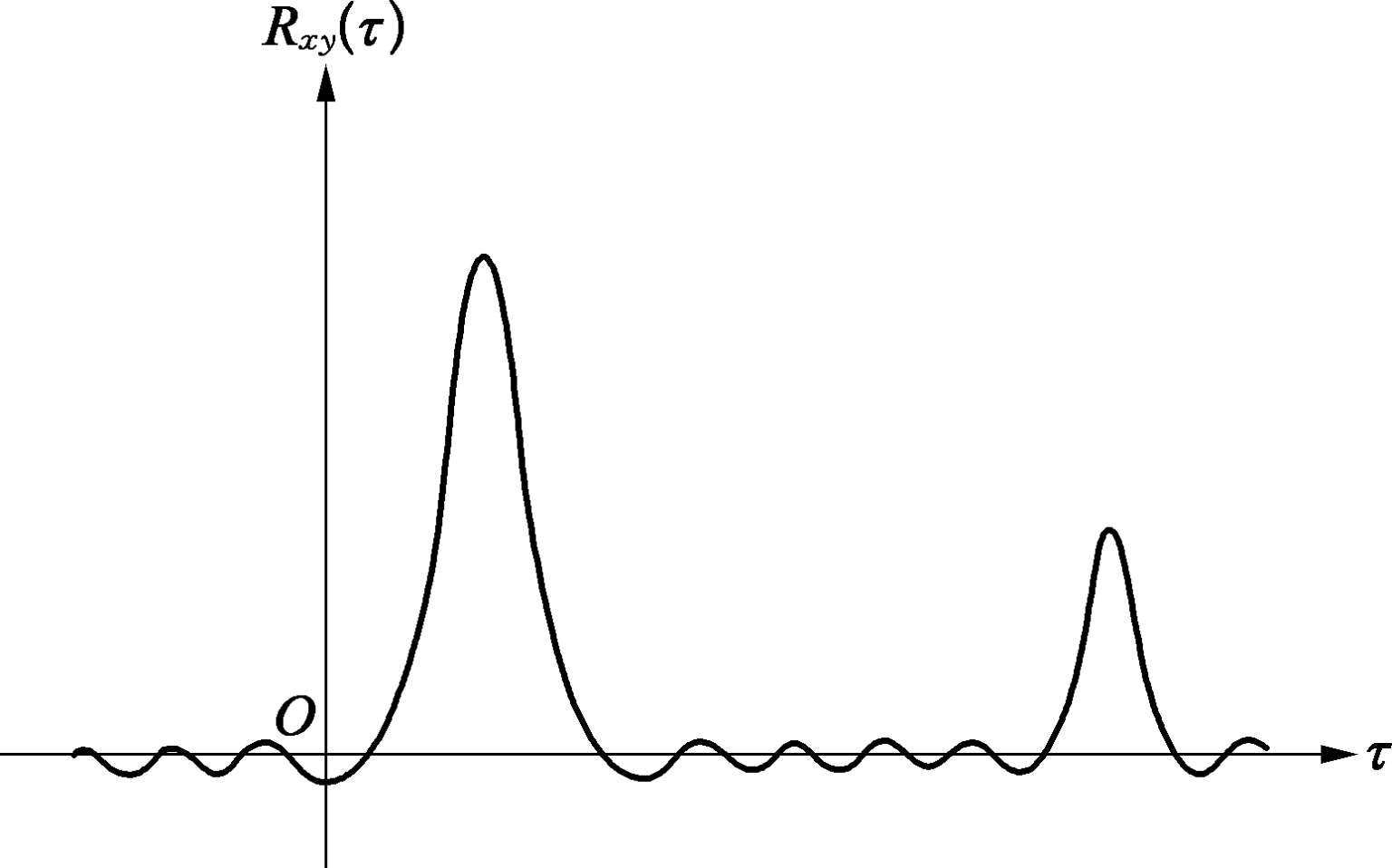
图2.5.2 典型的互相关函数
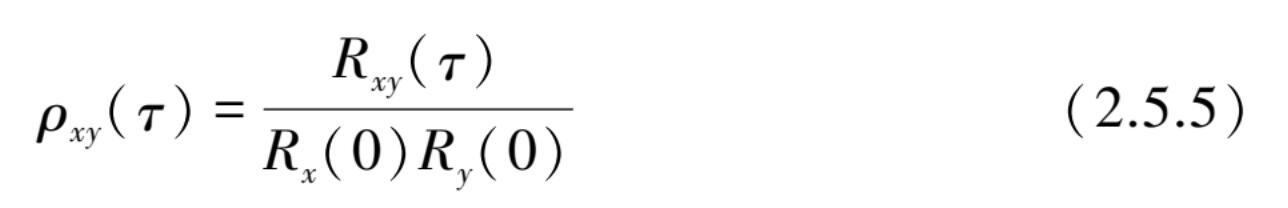
ρ xy 是在 0~1 之间变化的实数值,等于 1 时完全相关,等于零时不相关。
互相关函数在工程实际中主要有两方面的应用:
(1)传递通道的确定。用互相关函数可以建立时间滞后,从而可以直接来确定传递通道。例如在主控制室中要确定何种机械运转所引起的噪声和振动传递通道时,可建立和测量几种通道的设定(如建筑结构、空气传递等)。对于每个通道的输入和输出之间的相关性可通过互相关函数来测定,每个通道均具有不同的滞后时间,因此对输出如有明显影响的每个通道都会在互相关函数图中出现各自的峰值,从最短的位移时间和最明显的互相关值 R xy ( τ )[或 ρ xy ( τ )]上可找到噪声通道的源和最短时间通道路径。
(2)噪声中信号的拾取。对于隐藏在噪声中有用信号的检测,采用互相关函数比自相关函数更为有利,因为自相关分析不能从外部噪声中分离出所需要捡拾的有用无噪信号,而互相关分析可以提供一个更高的信噪比分析结果。
两组随机信号数据可直接从互相关函数的傅里叶变换获得互功率谱密度函数,即
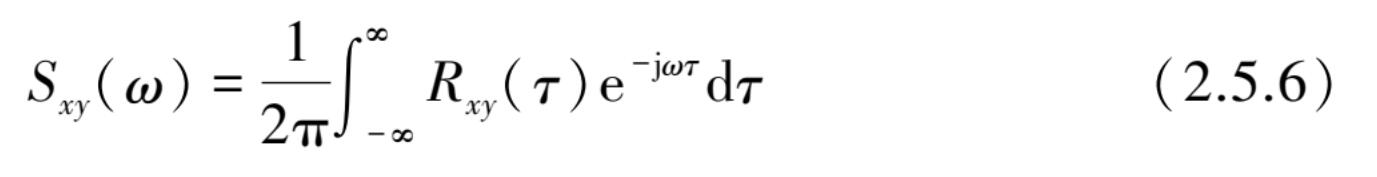
由于互相关函数不是偶函数,故互功率谱密度函数式(2.5.6)可以分解为实部 C xy ( ω )和虚部 Q xy ( ω )两部分。
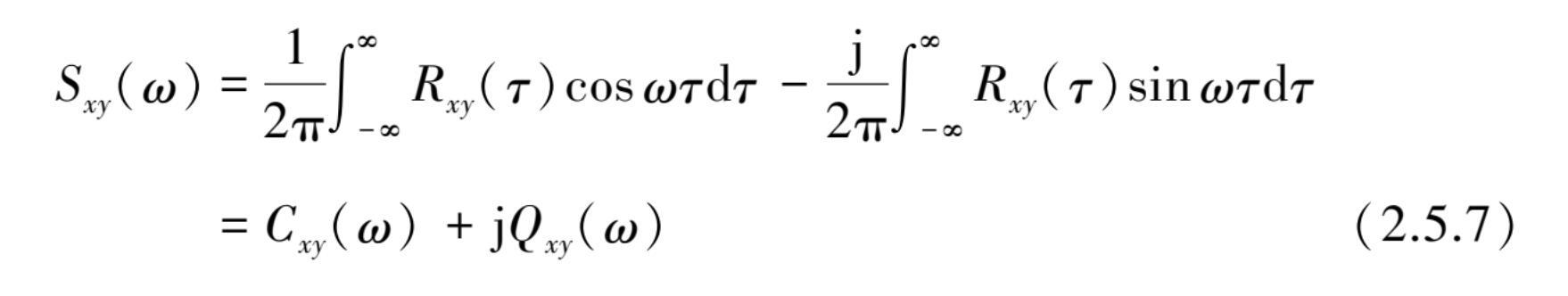
式中,实部 C xy ( ω )称为余谱(co-spectrum),虚部 Q xy ( ω )称为象限谱(quad-spectrum)。
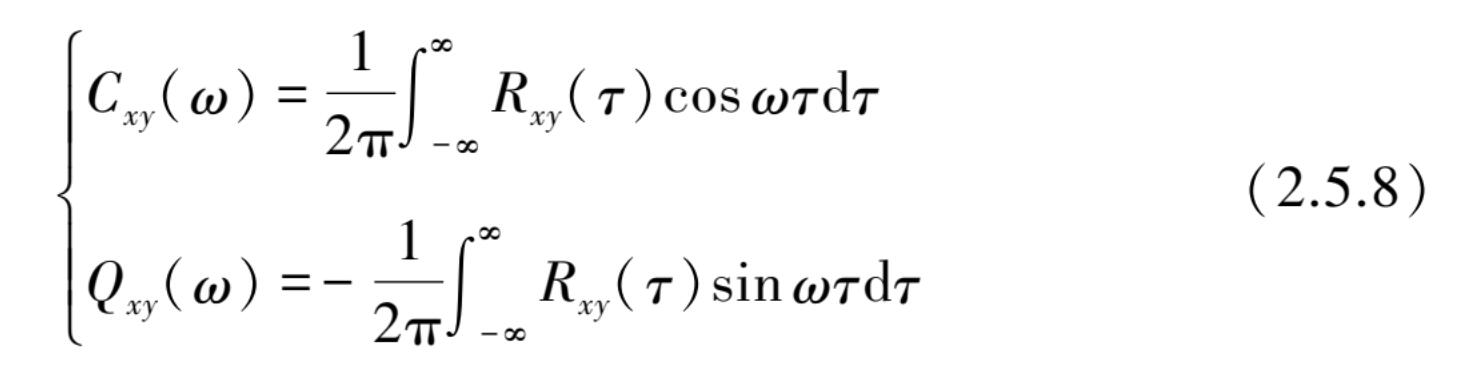
根据上式可知,
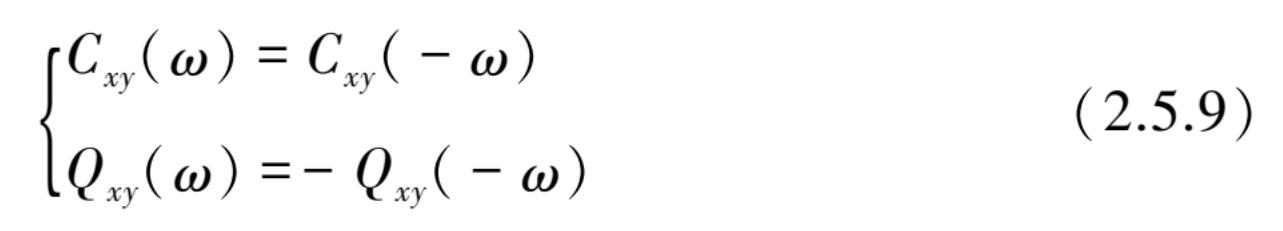
即 C xy ( ω )是 ω 的偶函数, Q xy ( ω )是 ω 的奇函数,同时也可证明 C xy ( ω )和 Q xy ( ω )另一个性质:
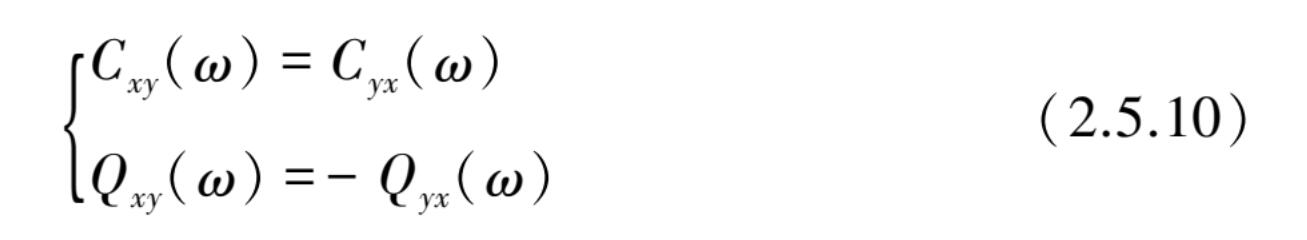
将式(2.5.6)用极坐标表示为
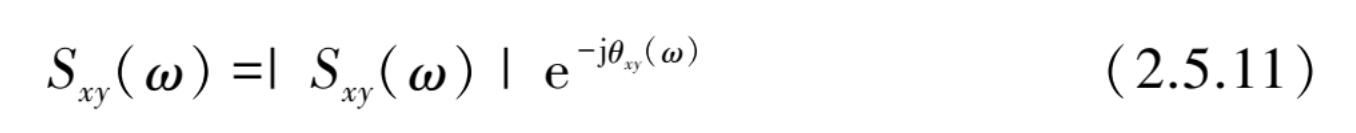
式中,幅值与相位角分别为
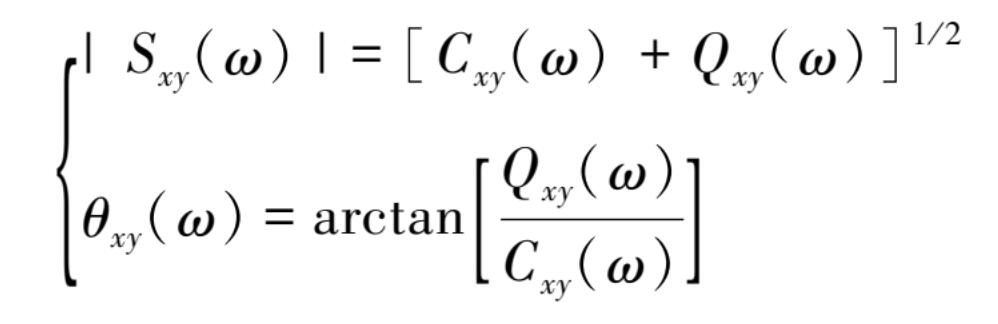
图 2.5.3 给出了一对典型随机时间历程的互功率谱密度与频率的关系曲线,该图给出了幅值和相位角。
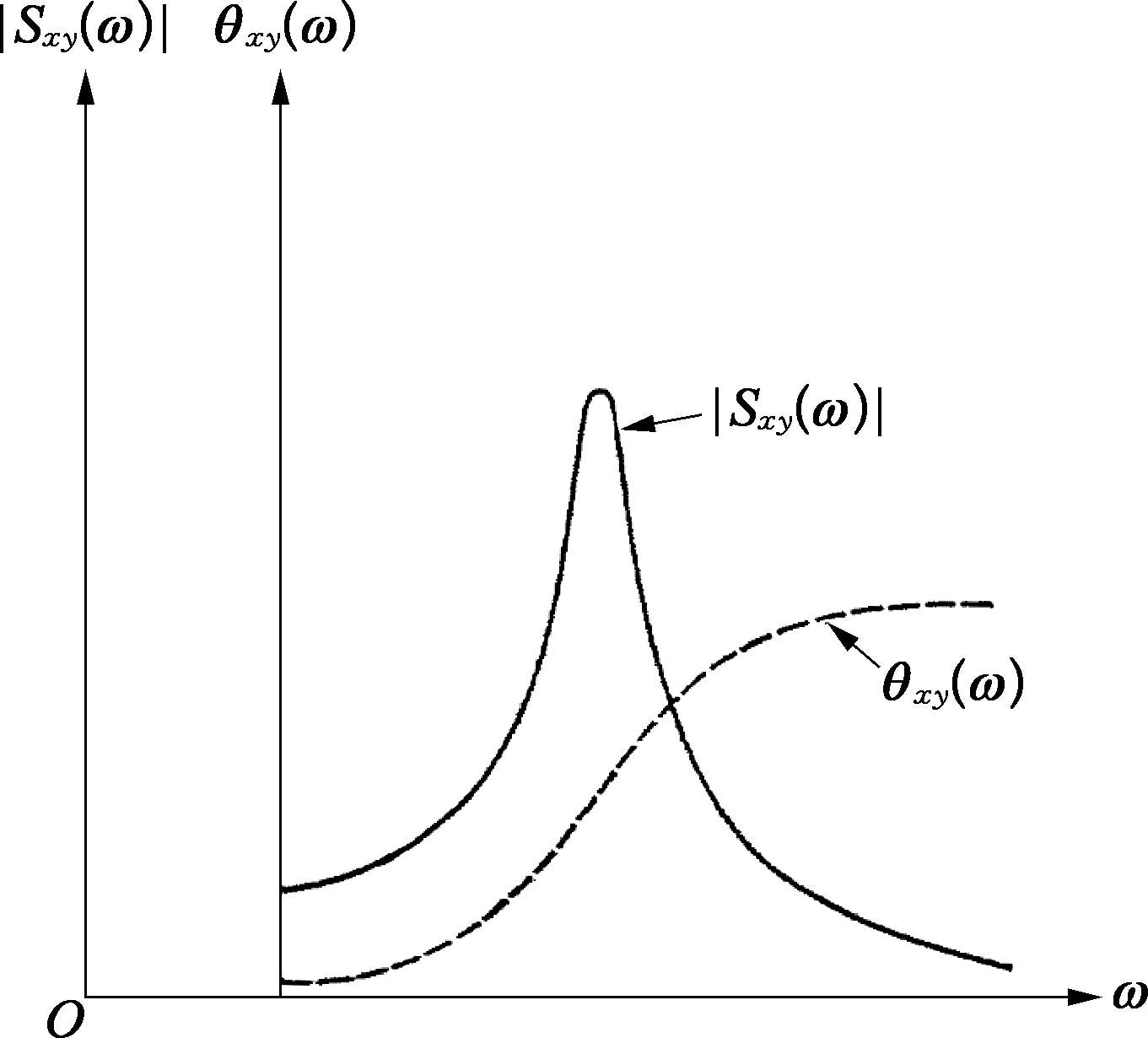
图2.5.3 典型的互功率谱密度
另一个很有用关系式为
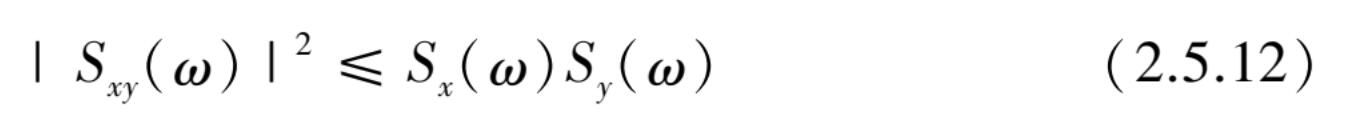
为此,互功率谱密度函数用在振动信号处理问题时,常采用相干函数
 (
ω
)来定义。
(
ω
)来定义。
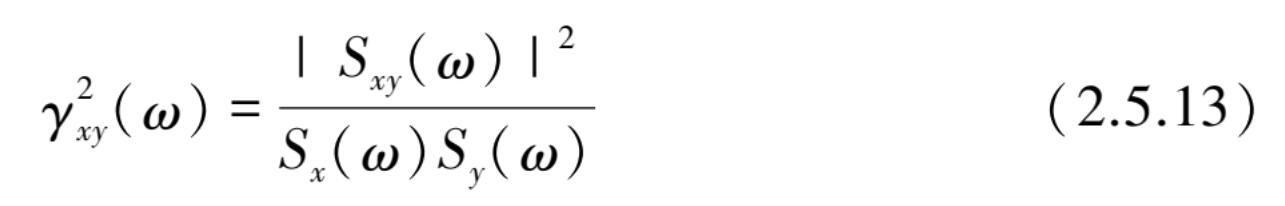
根据式(2.5.12)性质可知:

式(2.5.12)表明了当 x ( t )和 y ( t )在统计上如果是完全独立的(或完全相干),则 γ xy =1;如果是完全不独立的(或完全不相干),则 γ xy =0。
在实际中主要有以下两方面的应用:
(1)频率反应函数的测量。应用在振动系统测量时可以从振动系统的输入 x ( t )和输出 y ( t )信号获得互功率谱密度函数 S xy ( ω )和输入自功率谱密度 S x ( ω )的关系

式中, H (j ω )称为振动系统的传递函数,也可以根据式(2.5.15)按 H (j ω )= S xy ( ω ) / S x ( ω )来计算,其置信度可通过相干函数获得。
(2)滞后时间的测量。当振动系统的输入输出之间互谱的相位角为 θ xy ( ω )时,式(2.5.11)表明系统在频率域 ω 处的相位差,则可得到输入与输出信号之间的滞后时间 τ = θ xy ( ω )/ ω 。
随机信号 x ( t )的微分为
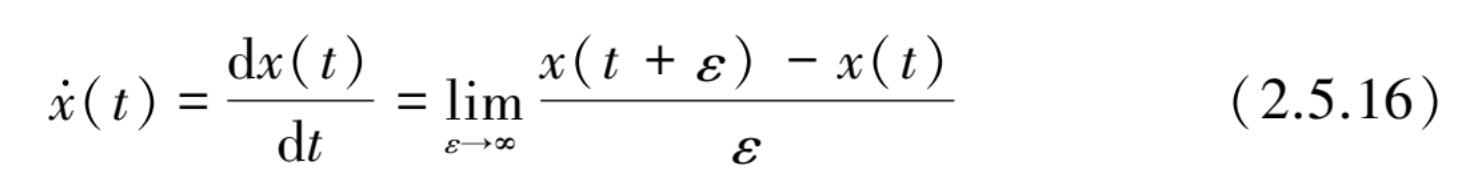
若对于
x
(
t
)的所有样本函数对上式中的极限都存在时,则
 (
t
)=
(
t
)=
 与通常确定性函数微分具有相同的意义。
与通常确定性函数微分具有相同的意义。
也就是说对 x ( t )在统计的均方值意义上存在上述极限的话,则称为在均方值意义上的 x ( t )存在可微分,数学上表示方差形式为
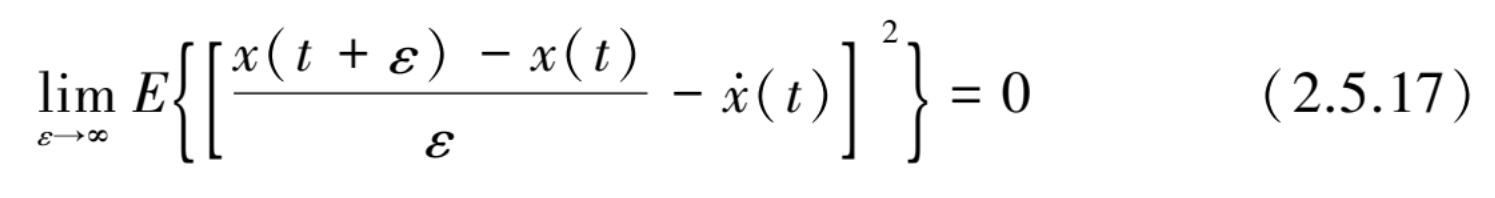
若满足式(2.5.17)的条件时,则认为 x ( t )在统计意义上可微,也就是根据式(2.5.16)可得到
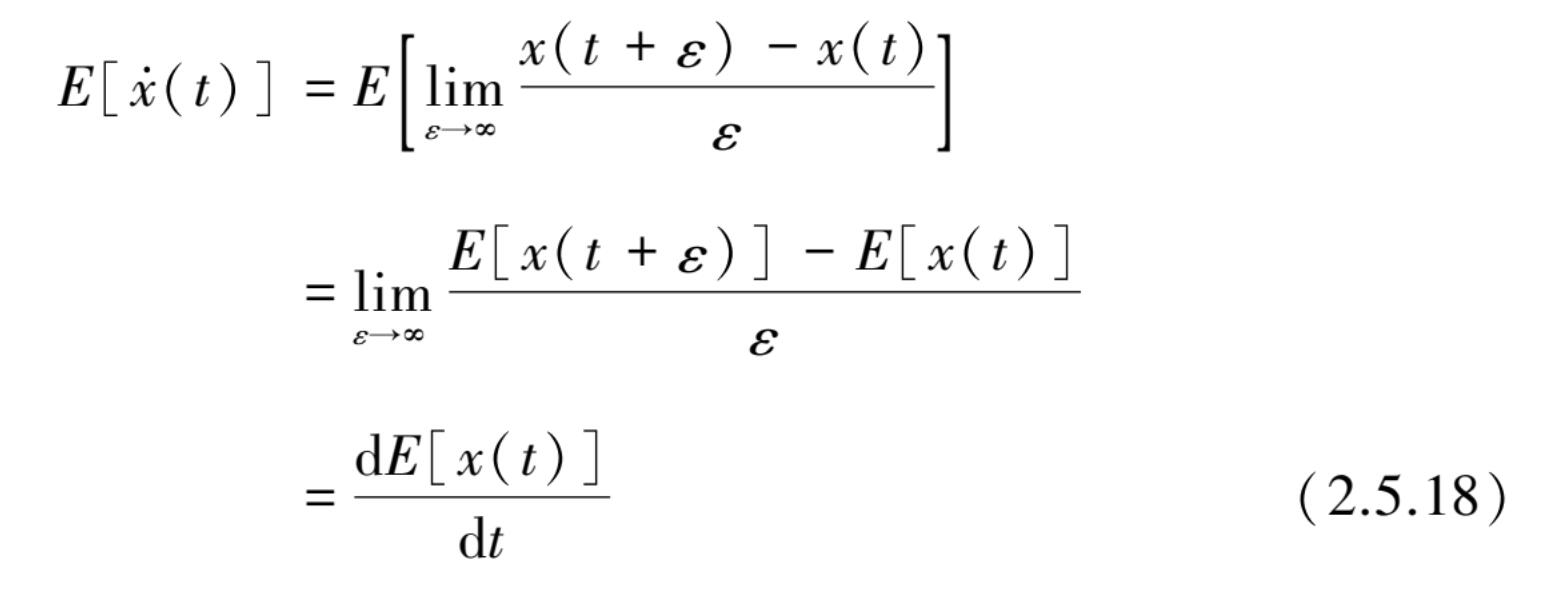
由上式可知, x ( t )求导的期望值等于 x ( t )期望值的微分。
 (
t
)在
t
1
,
t
2
时刻的自相关函数可取为
(
t
)在
t
1
,
t
2
时刻的自相关函数可取为
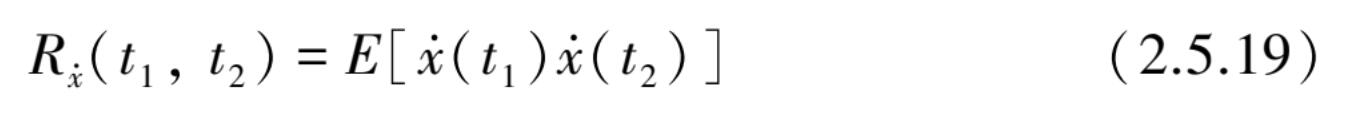
式中,
 =
=
 。
。
两个随机过程
x
(
t
)和
 (
t
)的互相关函数定义为
(
t
)的互相关函数定义为
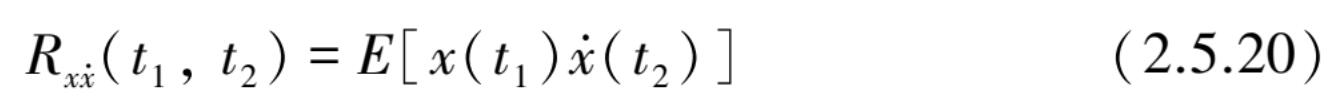
由于
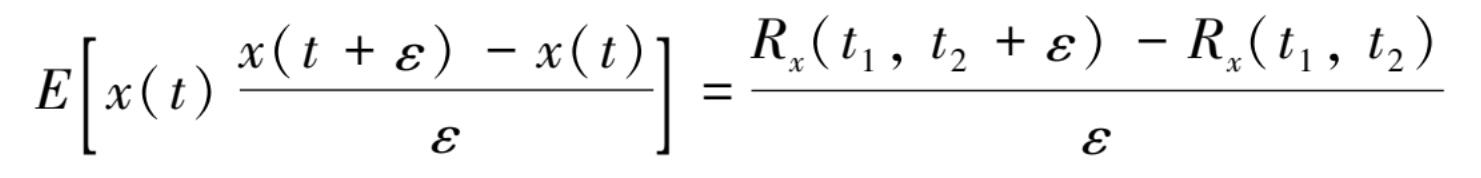
当 ε →0 时,则
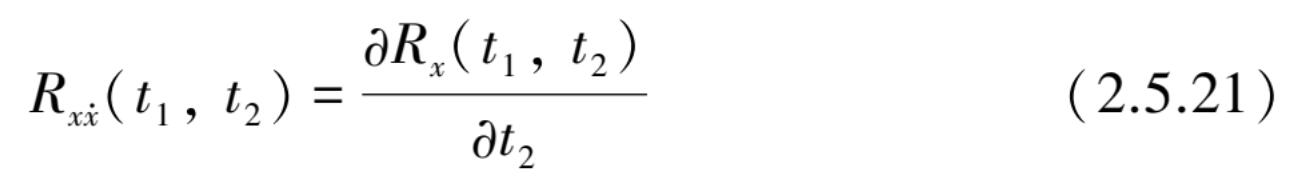
同理,由于
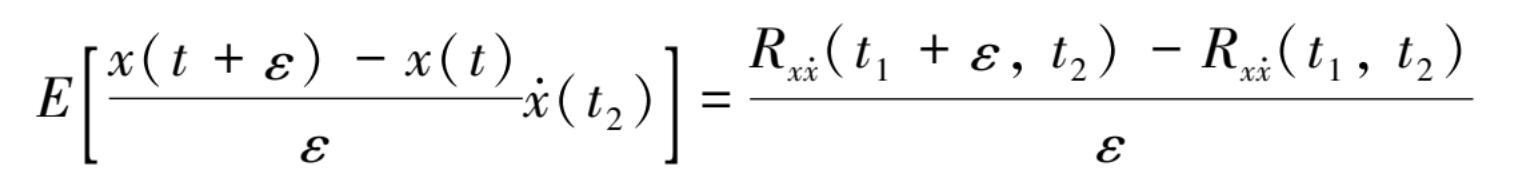
当 ε →0 时,则
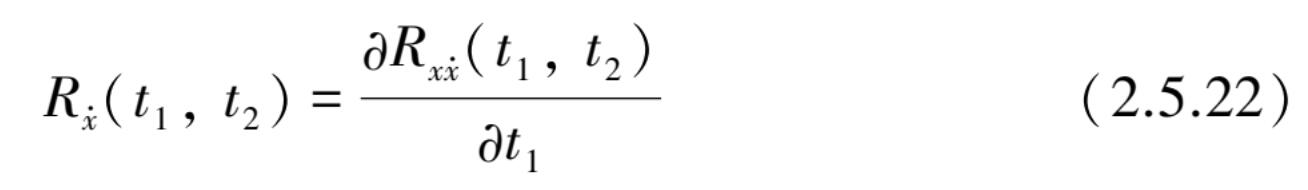
将式(2.5.21)代入式(2.5.22)后得到
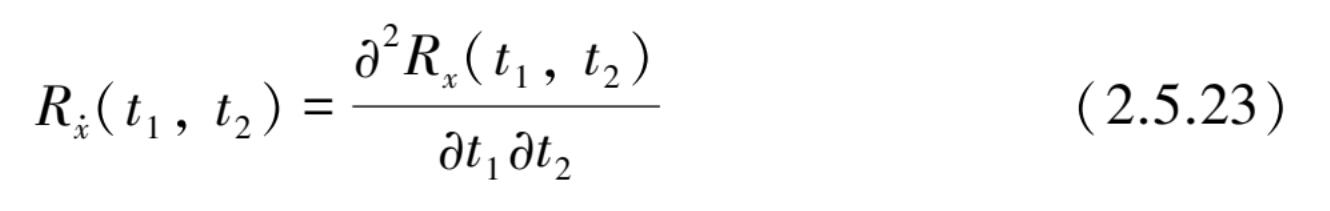
即为
 (
t
)的自相关函数,可按
x
(
t
)的自相关函数对
t
1
,
t
2
求偏导后得到。
(
t
)的自相关函数,可按
x
(
t
)的自相关函数对
t
1
,
t
2
求偏导后得到。
当特定的 x ( t )为平稳随机过程时,式(2.5.20)~式(2.5.23)中取 t 1 - t 2 = τ 代入后得
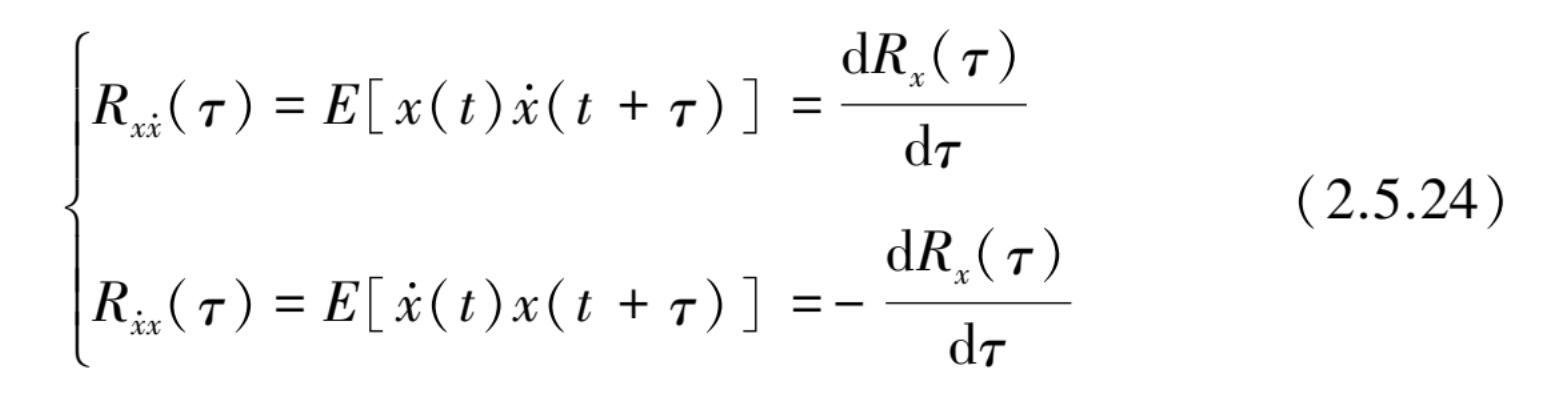
由此可得到
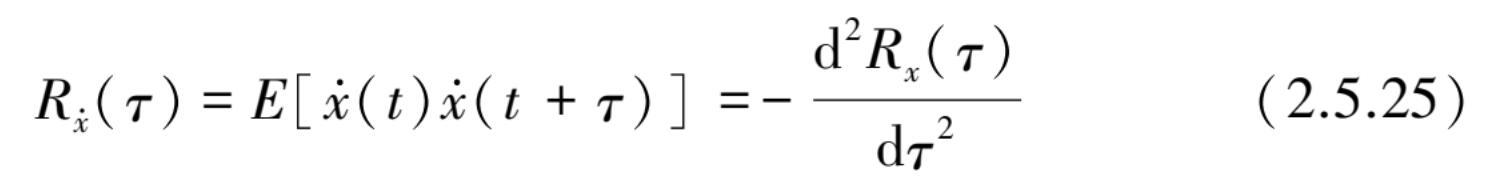
当上式取 τ =0,则
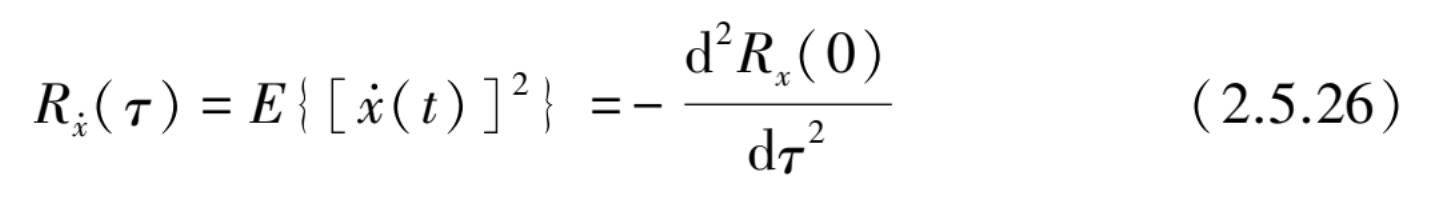
通常对应高次微分的通式可得到