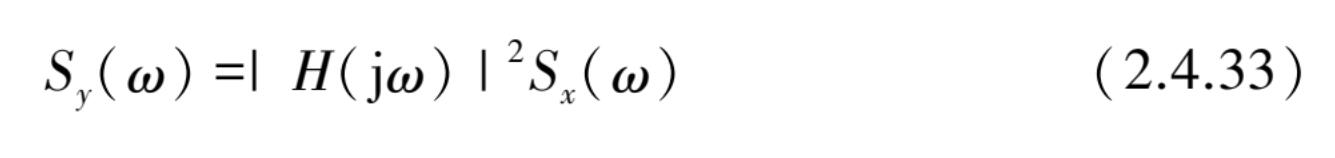在实际工程应用中通常采用 4 种主要统计函数来描述随机数据的基本特性:①均方值;②概率密度函数;③自相关函数;④功率谱密度函数。其中均方值是提供数据强度方面的基本描述;概率密度函数提供数据在振幅域内的有关特性;自相关函数和功率谱密度函数分别在时域和频域上提供有关信息。
下面以平稳随机数据为出发点阐述这些特性,并假设数据是各态历经的,从而可以用单个样本记录的时间统计平均来确定这些特性。
任何一组随机数据的一般强度可用均方值来描述,它是时间历程平方值的简单平均值。样本时间历程记录
x
(
t
)的均方值
 可表示为
可表示为
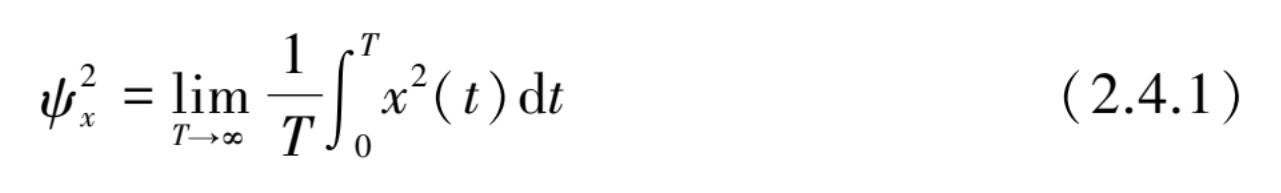
均方值的平方根 ψ x 称为均方根值,此物理数据可以认为是由静态分量(不随时间变化的分量)和动态分量(波动分量)之和所组成。静态分量可用均值来描述,即所有值的简单平均:
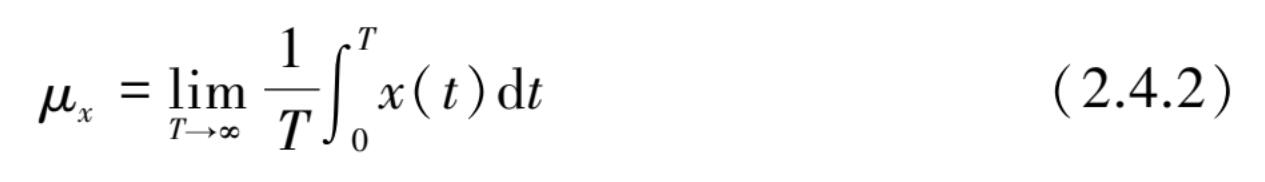
动态分量可以用与均值的方差
 来描述,是关于均值的简单均方值:
来描述,是关于均值的简单均方值:
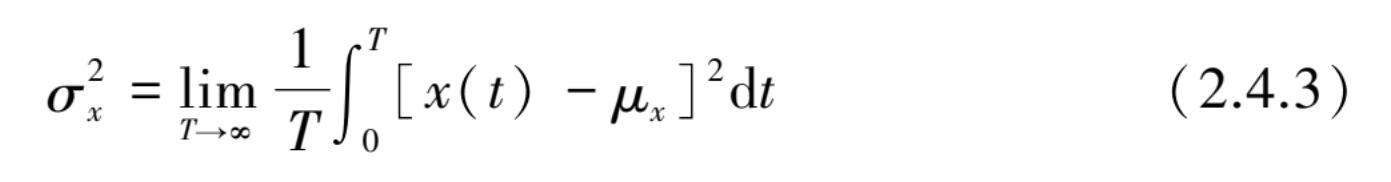
方差的平方根 σ x 称为标准差,由式(2.4.3)可以得到方差等于均方值减去均值的平方,即
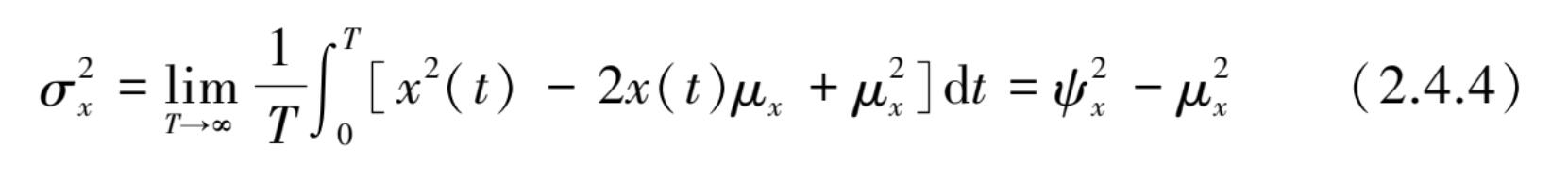
随机数据的概率函数表示瞬时数据值落在某指定范围内的概率。考虑图 2.4.1 所示的样本时间历程所记录的 x ( t ),对于 x ( t )值落在 x 和( x +Δ x )范围内的概率可由 T x / T 之比得到,这里 T x 是在观察时间 T 内, x ( t )落在( x , x +Δ x )范围内的总时间,当 T 趋向于无穷大时,此值将趋于一个确切的概率值 P rob 。
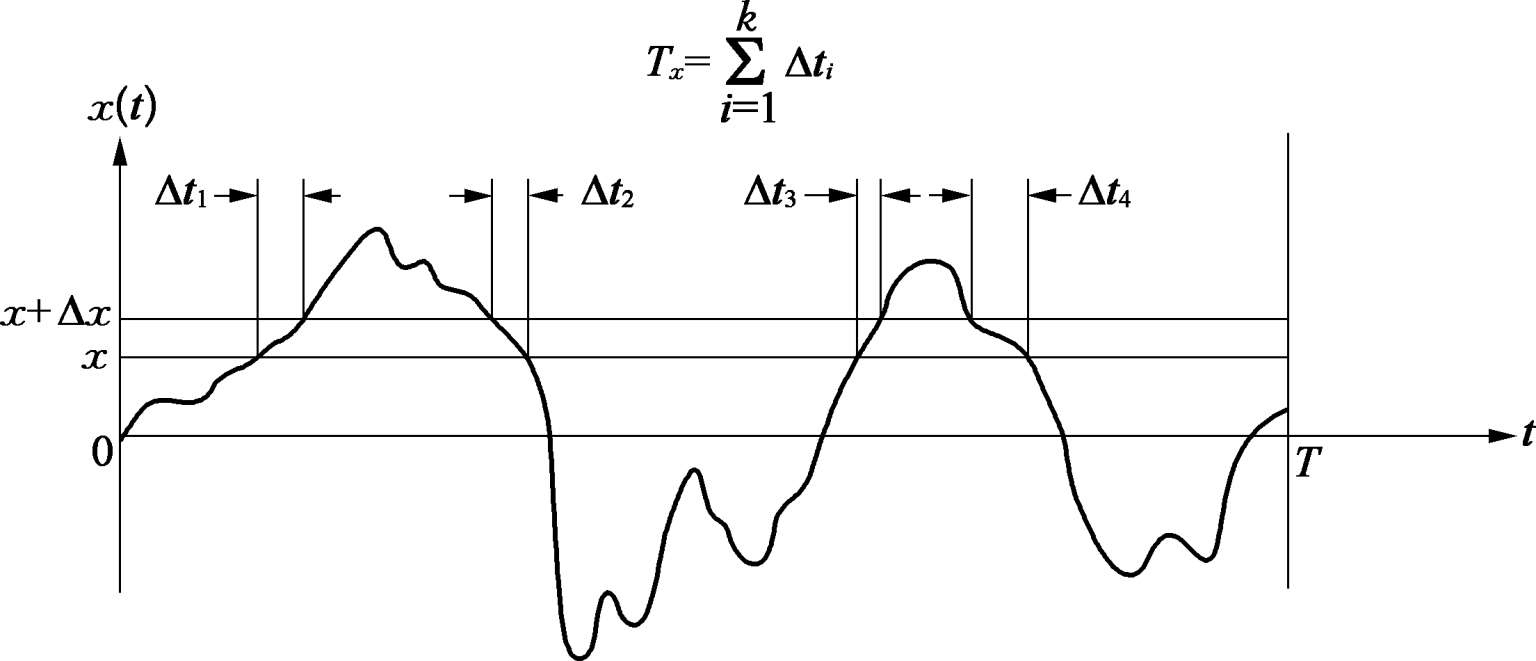
图2.4.1 概率测量方法
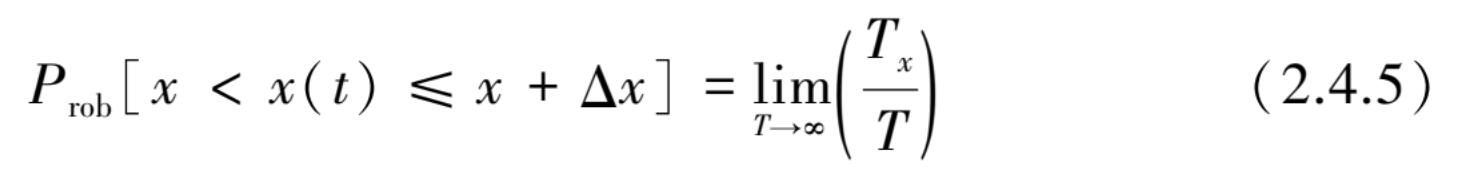
当Δ x 趋于无穷小时,可用概率密度函数 p ( x )表示为
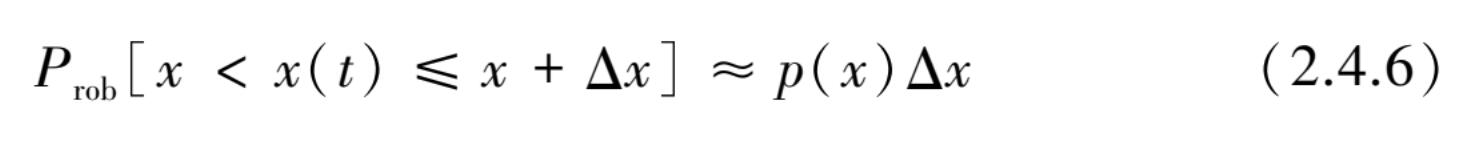
从中可推出 p ( x )为
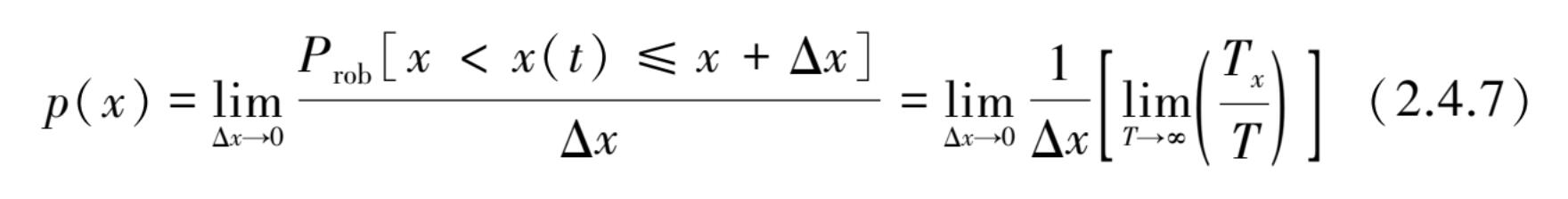
瞬时值 x ( t )小于或等于某值 x 的概率定义为 p ( x ),它等于概率密度函数 p ( x )从-∞到 x 的积分。 p ( x )称概率分布函数或累积概率分布函数,不应与概率密度函数 p ( x )相混淆,可表示为
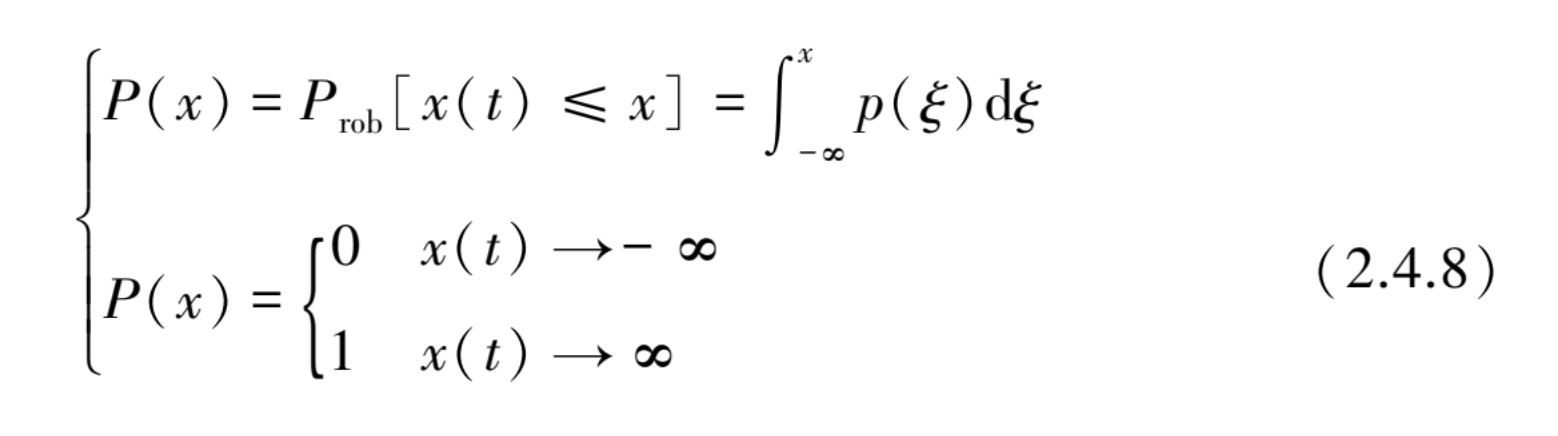
因为当 x ( t )趋向-∞的概率为 0 时, x ( t )趋向∞的概率为 1,所以概率分布函数的值一般应在 0 与 1 之间变化。
落在任何区域( x 1 , x 2 )内的概率为
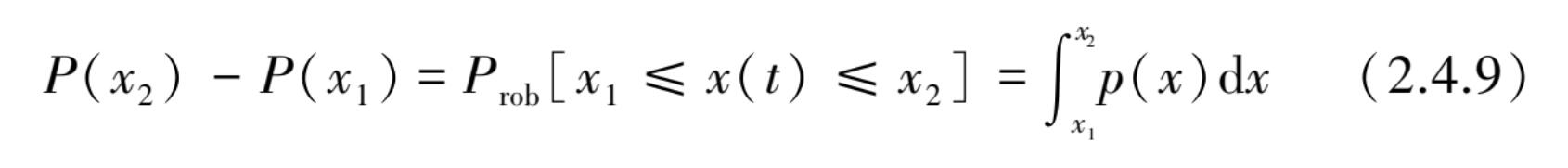
当用概率密度函数 p ( x )来表示 x ( t )的均值时,其值为 x ( t )在所有 x 值上的加权线性之和,可表示为

类似的,均方值可认为是 x 2 ( t )在所有 x 值的加权线性之和,可表示为

[例 1] 在实际测量中可能存在的 4 种样本时间历程记录:①正弦波;②正弦波加随机噪声;③窄带随机噪声;④宽带随机噪声。典型的时程记录如图 2.4.2 所示。所有记录假设均值为零( μ x =0)。
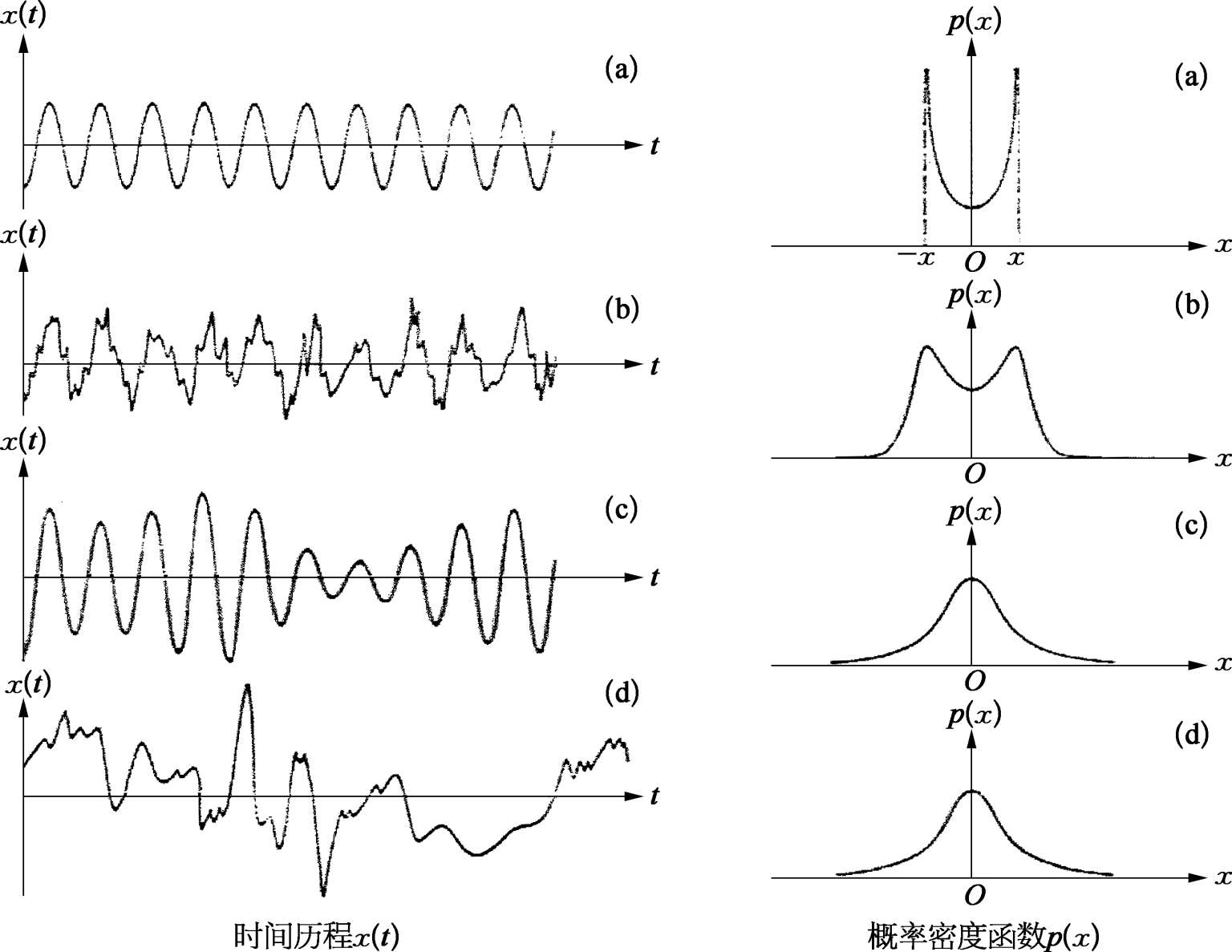
图2.4.2 4 个时间历程的概率密度函数
(a)正弦波;(b)正弦波加随机噪声;(c)窄带随机噪声;(d)宽带随机噪声
图 2.4.2(a)是正弦波的盆状概率密度函数曲线,对于正弦波曲线 x ( t )= X si n ( ω 0 t + θ )的概率密度函数为
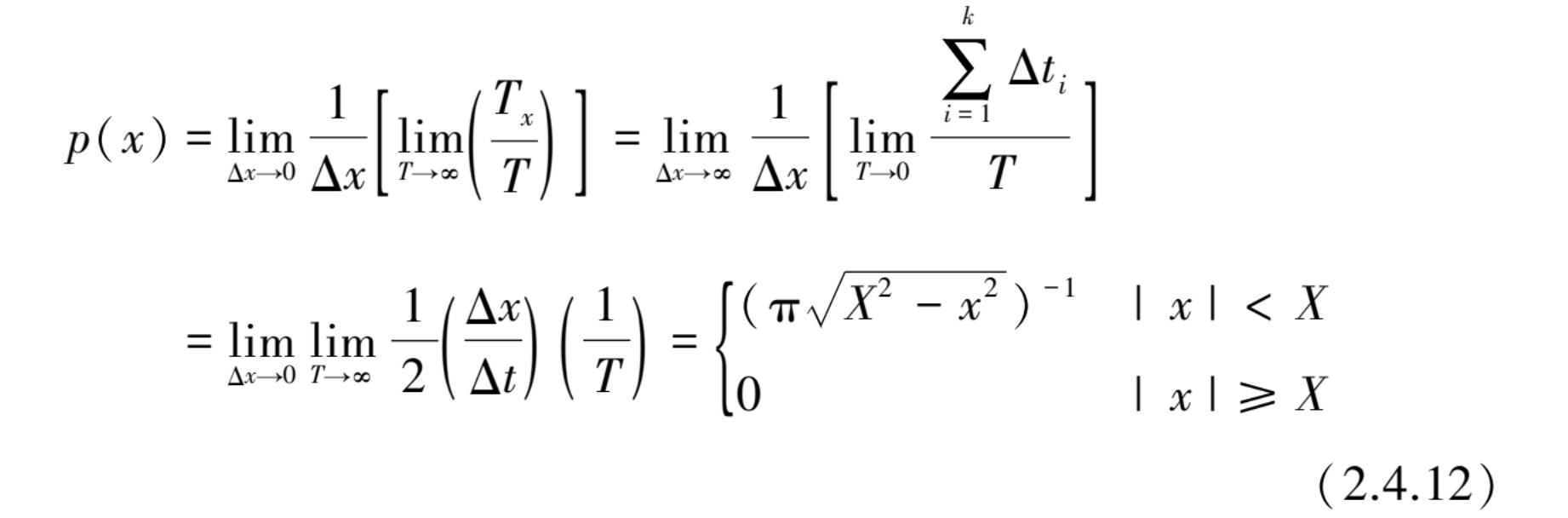
对于图 2.4.2(c),(d)所示的铃状概率密度图,分别表示为典型的窄带和宽带随机数据,这些概率密度取为经典的零均值高斯分布形式:
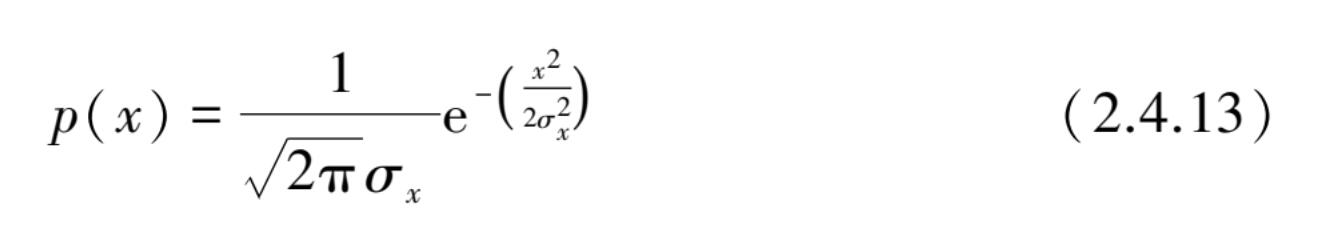
图 2.4.2(b)给出了正弦加随机噪声的概率密度图,该曲线具有图 2.4.2(a),(c)[或(d)]两种情况的综合特点。
概率密度函数主要应用于描述数据瞬时值的概率,也可以用作确定性数据和随机数据的区分。
随机数据的自相关函数主要是描述一个时刻的数据与另一个时刻数据之间的相互关系。对图 2.4.3 所示样本在时间历程记录 x ( t )上作在 t 时刻和( t + τ )时刻之间的相关性估计时,则可以在总时间区间T内由这两个值的乘积对时间 t 的平均得到。当 T 趋于无穷时,平均乘积的极限值将接近一个确切的自相关函数。
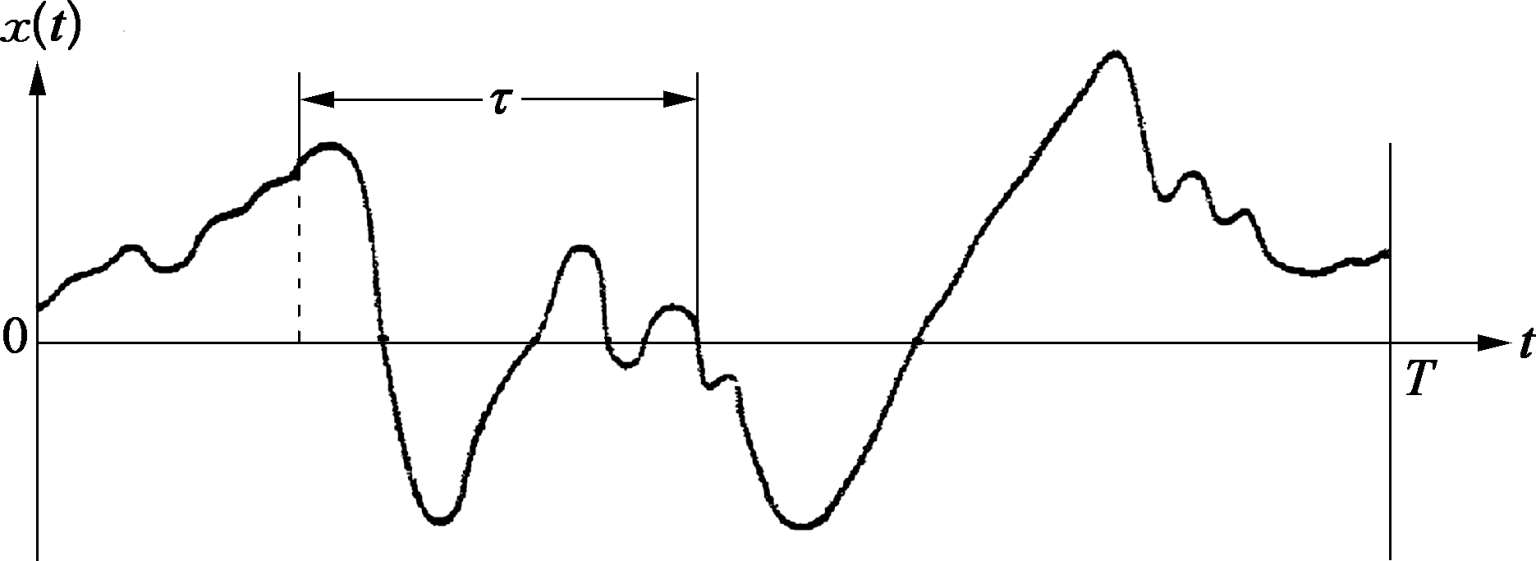
图2.4.3 自相关测量
自相关函数可表示为
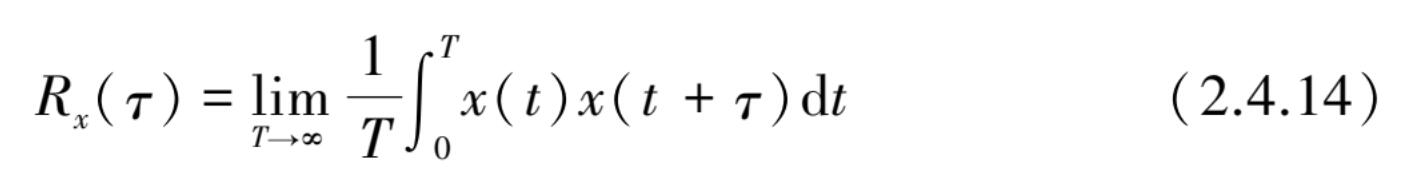
R x ( τ )是恒定的实偶函数,在 τ =0 时有最大值,即

由 R x ( τ )的性质可知, x ( t )的均值和均方值为

[例 2] 图 2.4.4 给出了图 2.4.2 中 4 个时间历程所对应的自相关函数 R ( τ )时间位移 τ 的曲线。
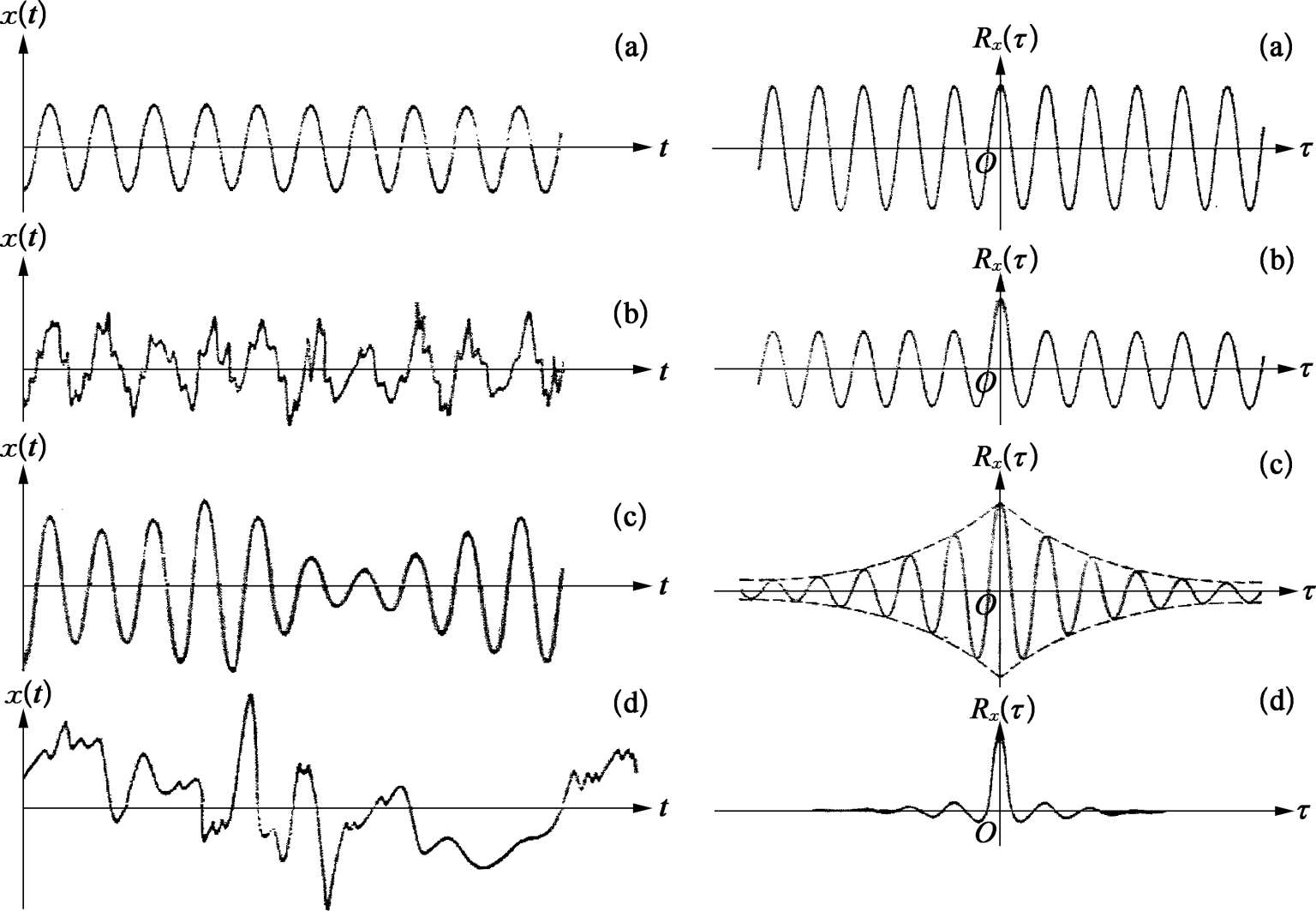
图2.4.4 自相关函数图形
(a)正弦波;(b)正弦波加随机噪声;(c)窄带随机噪声;(d)宽带随机噪声
图 2.4.4(a)为一个正弦波 X sin ω 0 τ 所对应的自相关函数:

在 R ( τ )对于时间位移 τ 历程上,具有与原始正弦波相同的周期(或频率 ω 0 ),但其相位角消失了。
图 2.4.4(d)是宽带随机数据典型的自相关函数图,
R
(
τ
)随时间位移
τ
很快衰减至零(如均值
μ
x
不为零时,则自相关函数衰减到
 值)。若是白噪声的极限状况,对应的
R
(
τ
)在
τ
=0 处是一个
δ
脉冲函数。
值)。若是白噪声的极限状况,对应的
R
(
τ
)在
τ
=0 处是一个
δ
脉冲函数。
图 2.4.4(b)是正弦波加随机函数所对应的 R ( τ ),这是正弦波的自相关图与随机函数的自相关函数之和。
图 2.4.4(c)是窄带随机噪声所对应的 R ( τ ),这是正弦波自相关函数出现衰减形状曲线,当时间位移 τ 很大时,自相关函数将趋于零(假设 μ x = 0)。该图说明了从正弦波到宽带随机噪声信号,对应自相关函数 R ( τ )与概率密度函数一样,有明确变化趋势的确定性统计值数据,所以相关函数的功能主要是能够检测和辨别出混淆在随机信号中的确定性信号数据。自相关函数的傅里叶变换是自功率谱密度函数,它们分别表征在时域 τ 上和频域上的有关信息。
自功率谱密度函数定义为随机信号数据
x
(
t
)通过中心频率为
f
、带宽为Δ
f
的窄带滤波器后,获得时间历程
x
(
t
,
f
,Δ
f
)的均方值。当带宽Δ
f
趋向于零、平均周期
T
趋向无穷大时,其均方值
 f
,Δ
f
)的极限称为随机信号
x
(
t
)的功率谱密度函数(PSD)。其表达式为
f
,Δ
f
)的极限称为随机信号
x
(
t
)的功率谱密度函数(PSD)。其表达式为
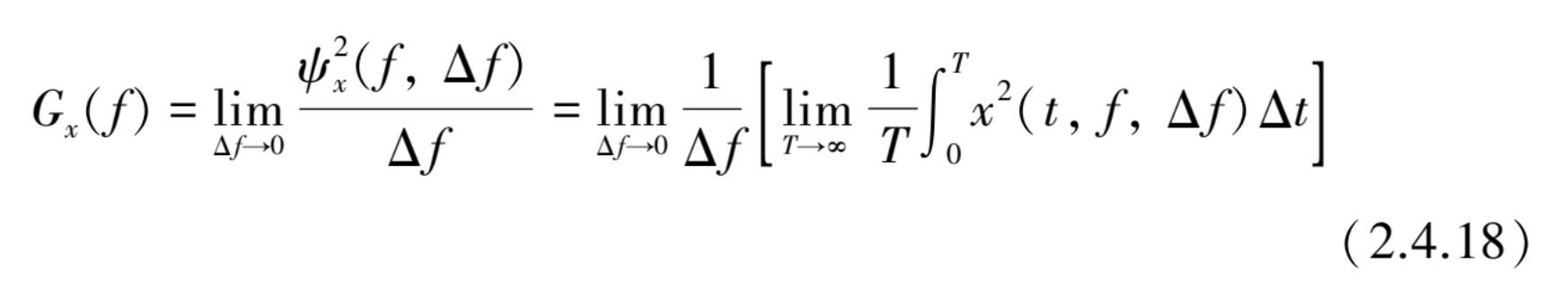
自功率谱密度函数 G x ( f )恒为一个非负的实数数值。它的一个重要的性质是与自相关函数相互成傅里叶变换关系。
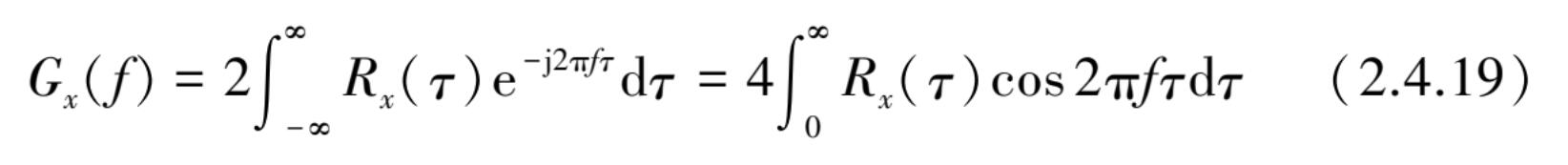
而 R x ( τ )为 G x ( f )的傅里叶反变换,即
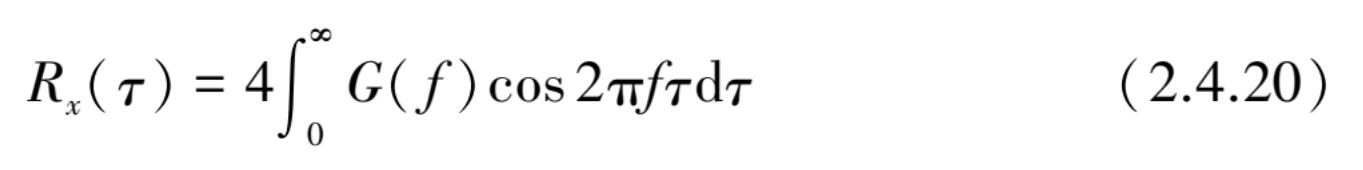
在不同书籍中使用的功率谱密度函数表达方式是不同的,最常见的是采用圆频率 ω 作为变量定义为双边功率谱密度函数 S x ( ω ), S x ( ω )与 R x ( τ )之间的傅里叶变换关系为
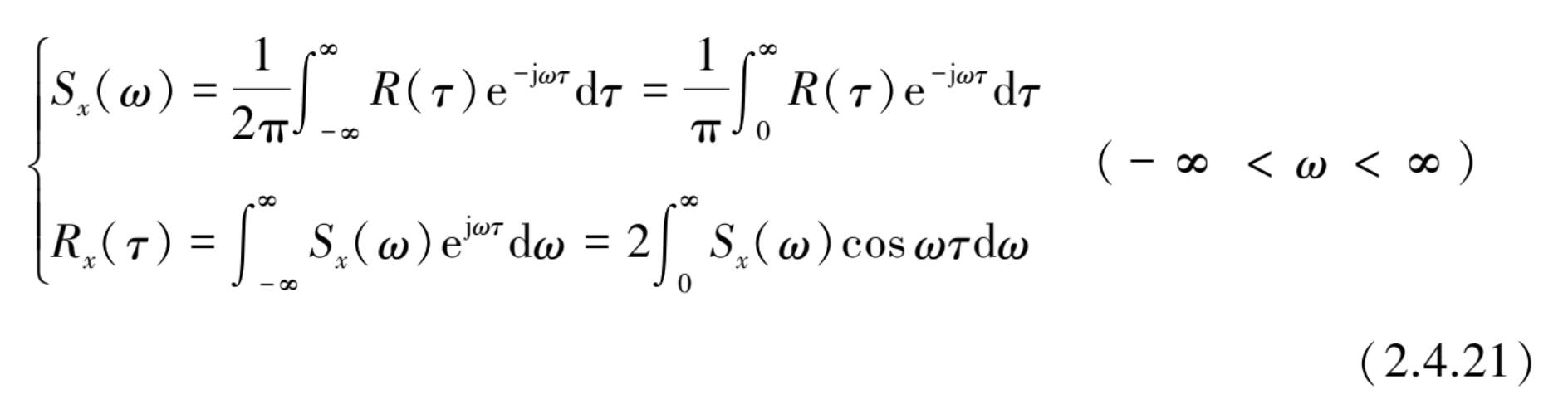
双边功率谱密度函数 S x ( ω )与单边功率谱密度函数 G x ( f )之间关系式为

另外,也有文献将 S x ( ω )中变量圆频率 ω 用频率 f 来表示,其 f 的区域扩展至(-∞< ω <∞)范围。这时 S x ( f )与 G x ( f )的关系为
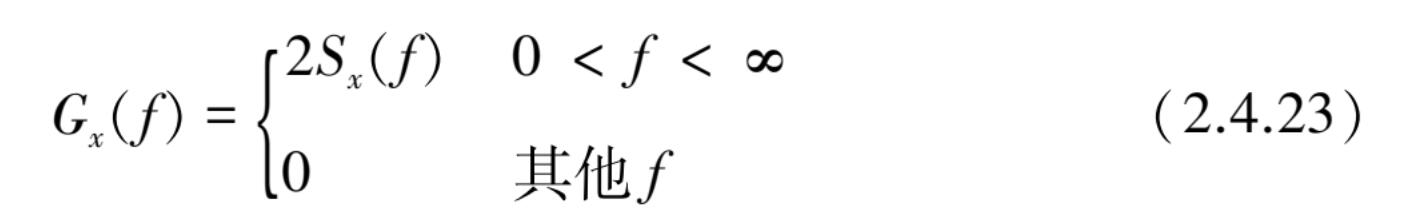
综上,有关系式
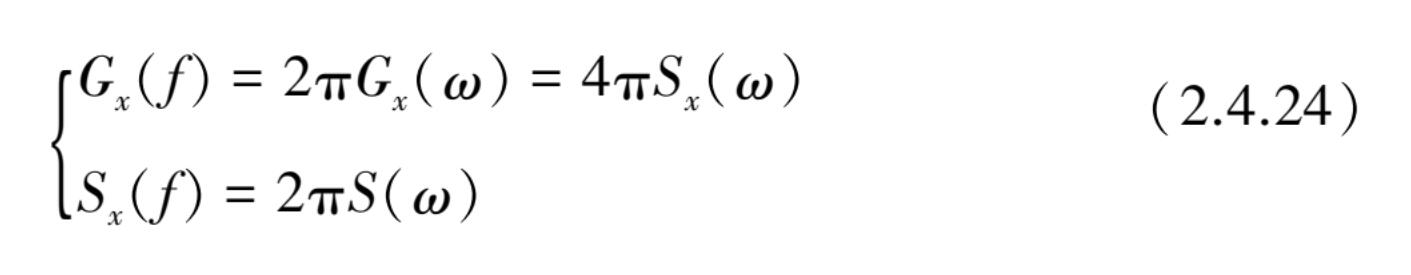
对于 S x ( ω )和 G x ( ω )之间的关系如图 2.4.5 所示,即将偶函数 S x ( ω )的后半部折算到右边再叠加起来就等于 G x ( ω ),乘上 2π就等于 G x ( f )。
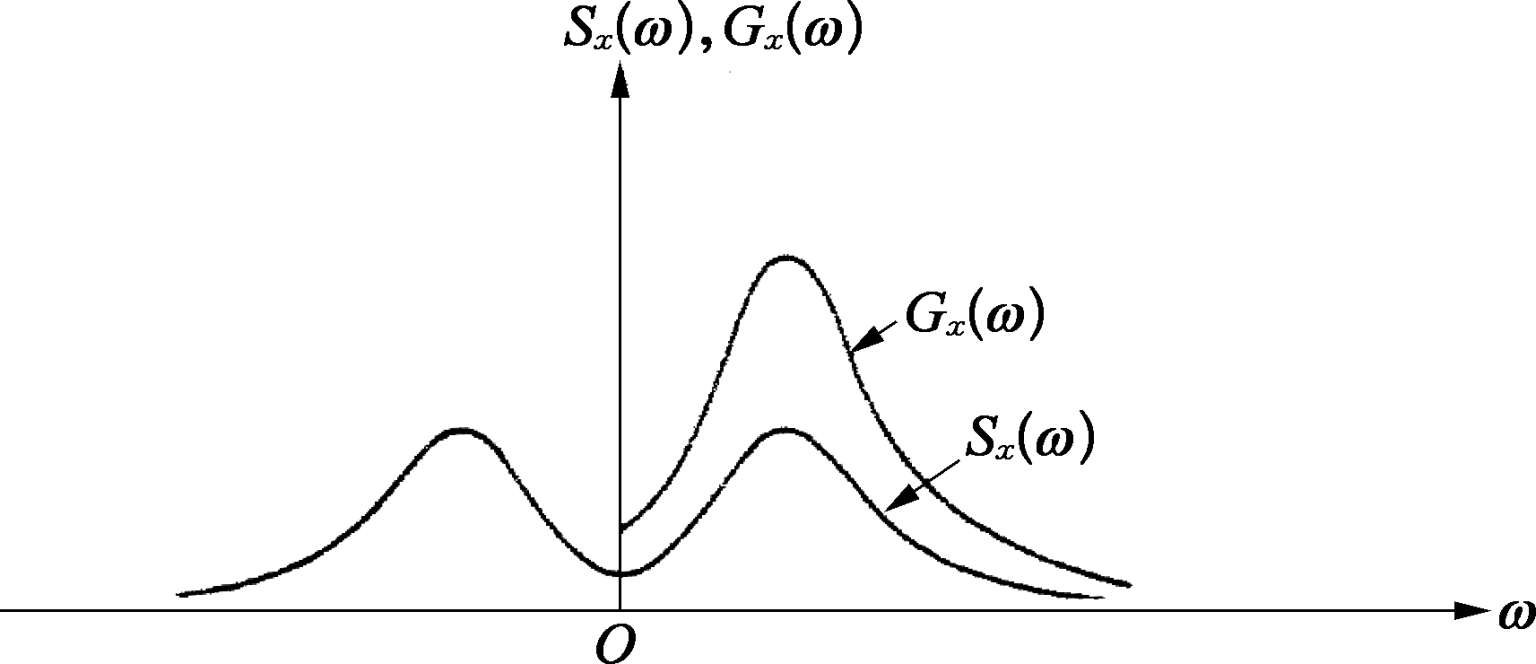
图2.4.5 功率谱密度函数 S x ( ω )和 G x ( ω )之间关系
要注意的是,不同书籍和文献中所采用的双边功率谱密度函数 S x ( ω )与相关函数 R x ( τ )之间的傅里叶变换与式(2.4.21)基本形式有差别,附录H专门论述不同傅里叶变换格式对PSD估计是没有任何影响的。
功率谱密度函数与均方值之间的关系可用如下方法来推导。设 A x ( ω )为 x ( t )的傅里叶谱,为复函数。
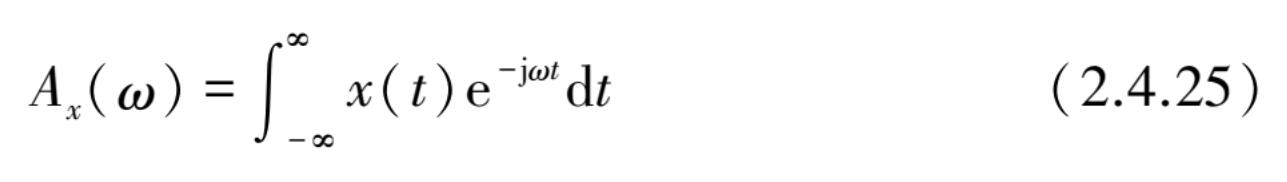
则 A x ( ω )的傅里叶反变换为
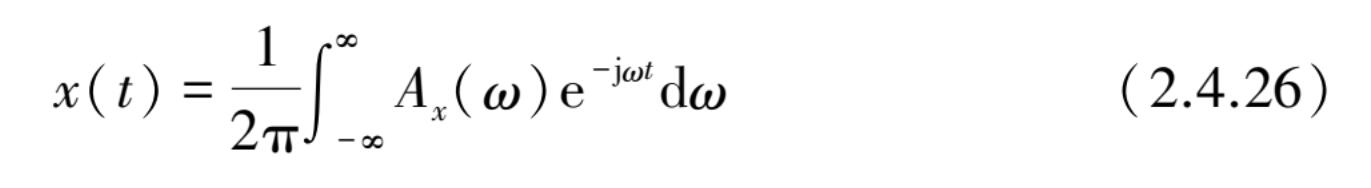
x ( t )的均方值定义为
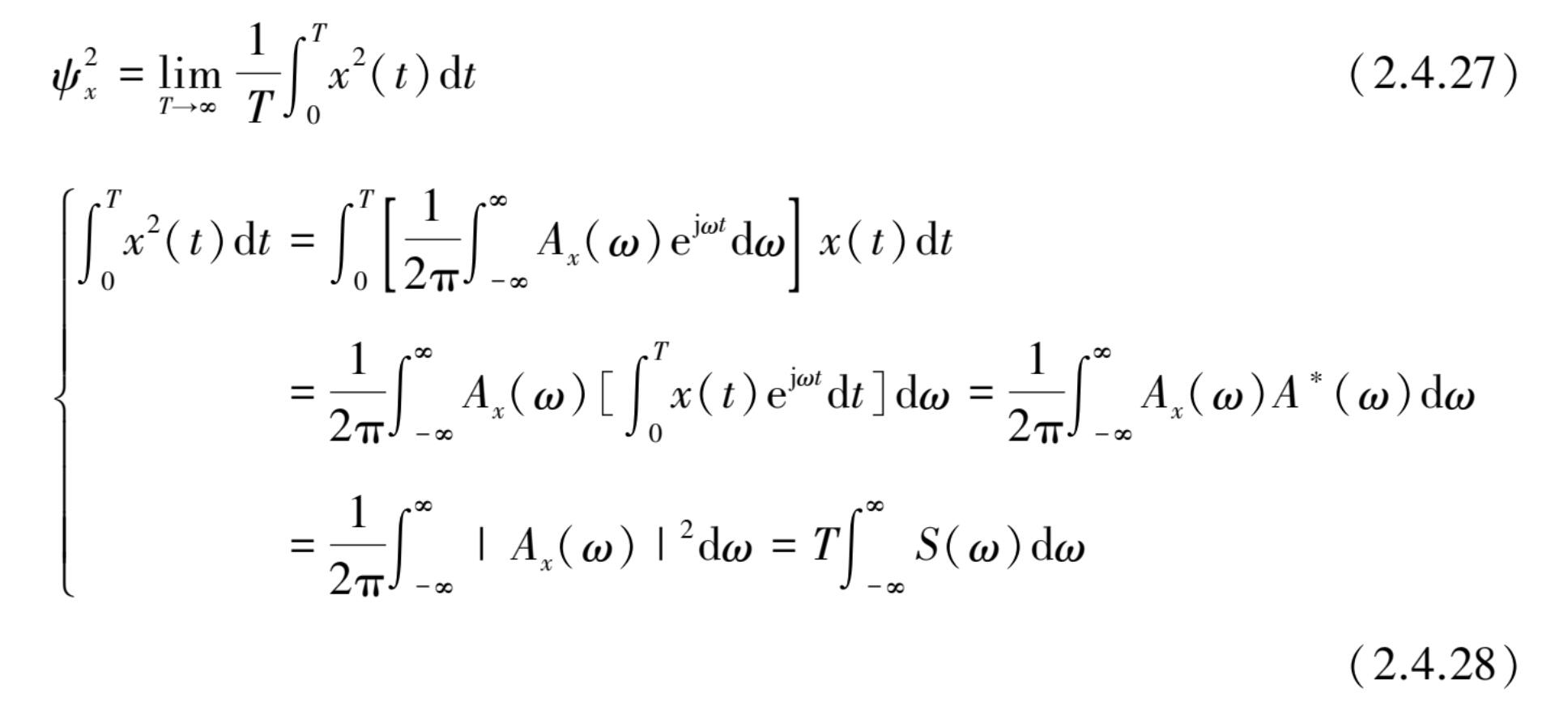
式中, A * ( ω )为 A ( ω )的共轭复数,即 A * (j ω )= A (-j ω )。
由式(2.4.28)可得到
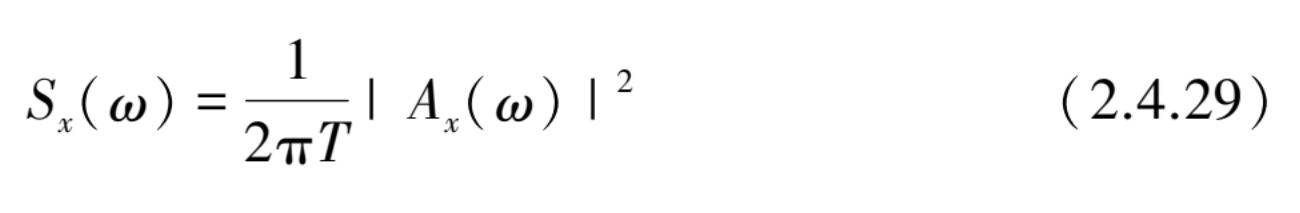
同时代入式(2.4.27)得到

由式(2.4.22)中 G x ( f )与 S x ( ω )的关系,可得

图 2.4.6 展示了 6 种有代表性的
S
x
(
ω
)和
R
x
(
τ
)之间关系图汇总结果,图 2.4.6(e)中功率谱密度等于常数[
S
x
(
ω
)=常数],称之为“白噪声”,其
 和
ω
轴所围的面积
和
ω
轴所围的面积
 ,即均方值为无限大,是实际上不存在的随机过程。但由于
S
x
(
ω
)的表达式简单,在理论分析上还经常得到应用。
,即均方值为无限大,是实际上不存在的随机过程。但由于
S
x
(
ω
)的表达式简单,在理论分析上还经常得到应用。
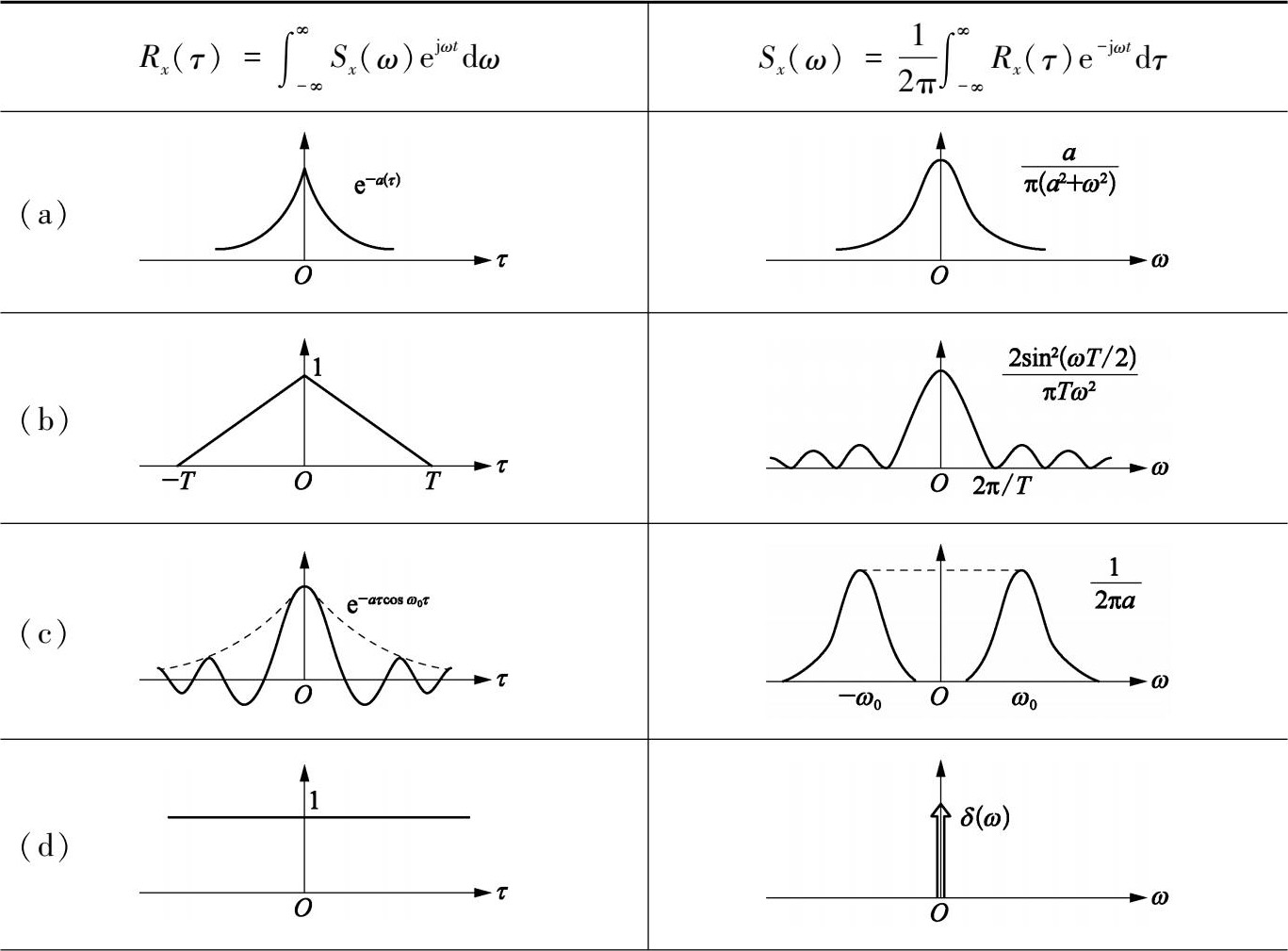
(续表)
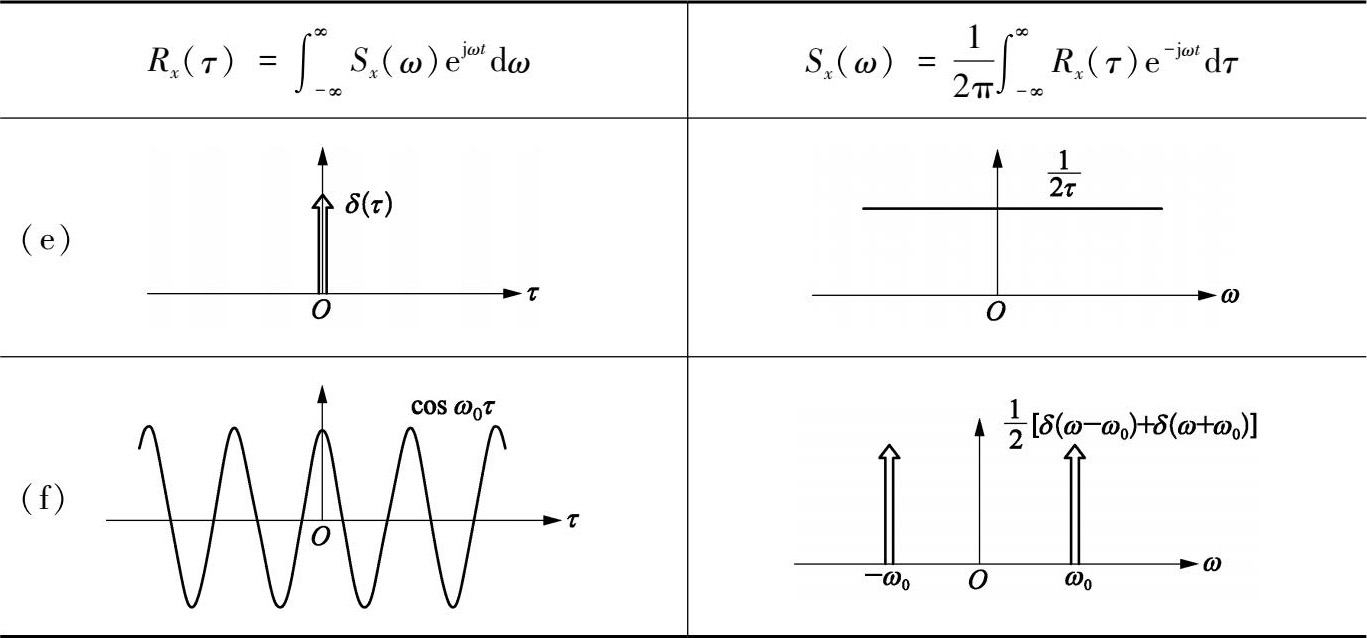
图2.4.6 自相关函数与功率谱密度函数对应关系
[例 3] 图 2.4.7 给出了图 2.4.2 中 4 个相同时间历程所对应的功率谱密度函数 S ( ω )对于频率 ω 的关系图。
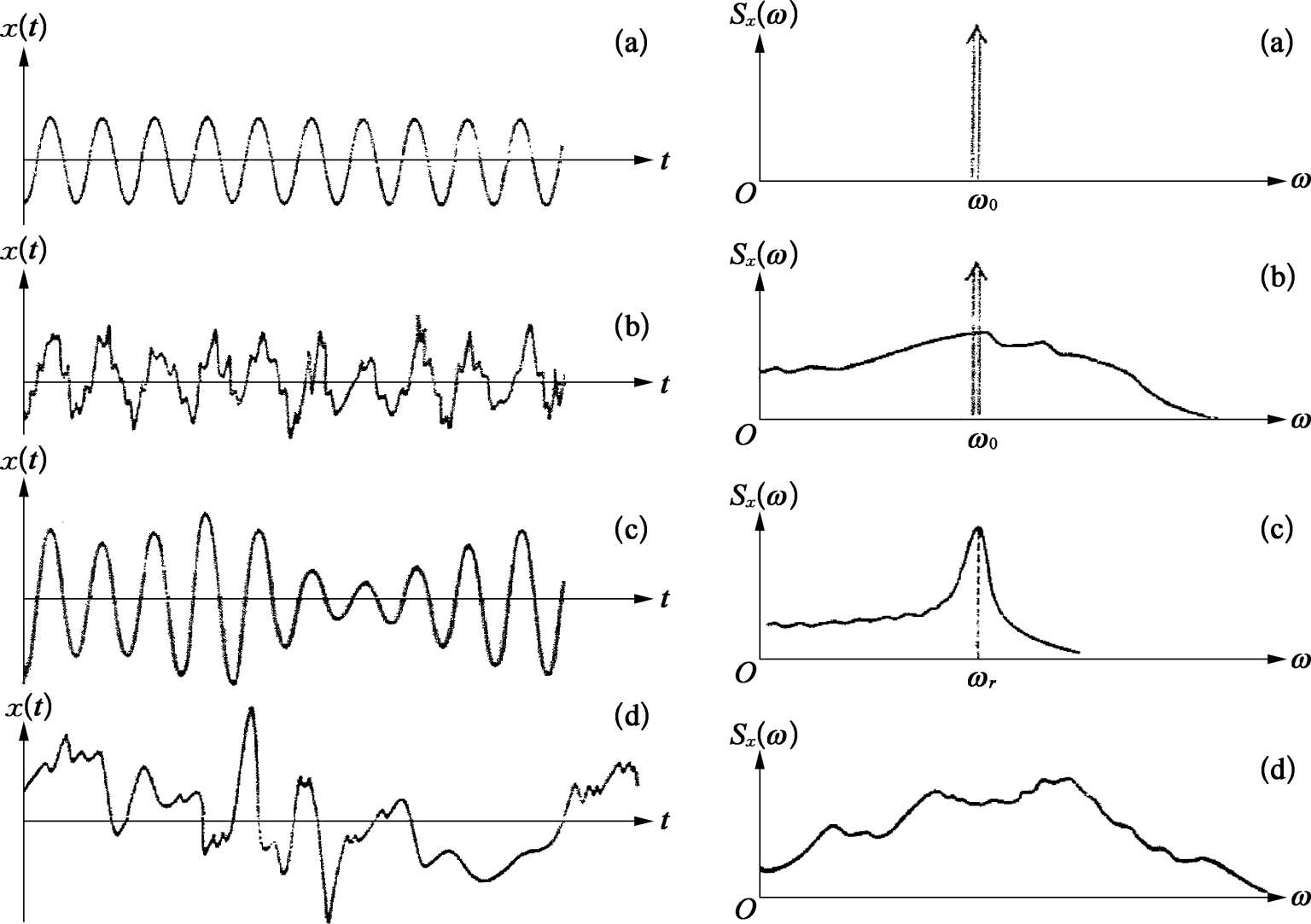
图2.4.7 功率谱密度函数
(a)正弦波;(b)正弦波加随机噪声;(c)窄带随机噪声;(d)宽带随机噪声
图 2.4.7(a)表示式(2.2.1)正弦波的功率谱密度函数:
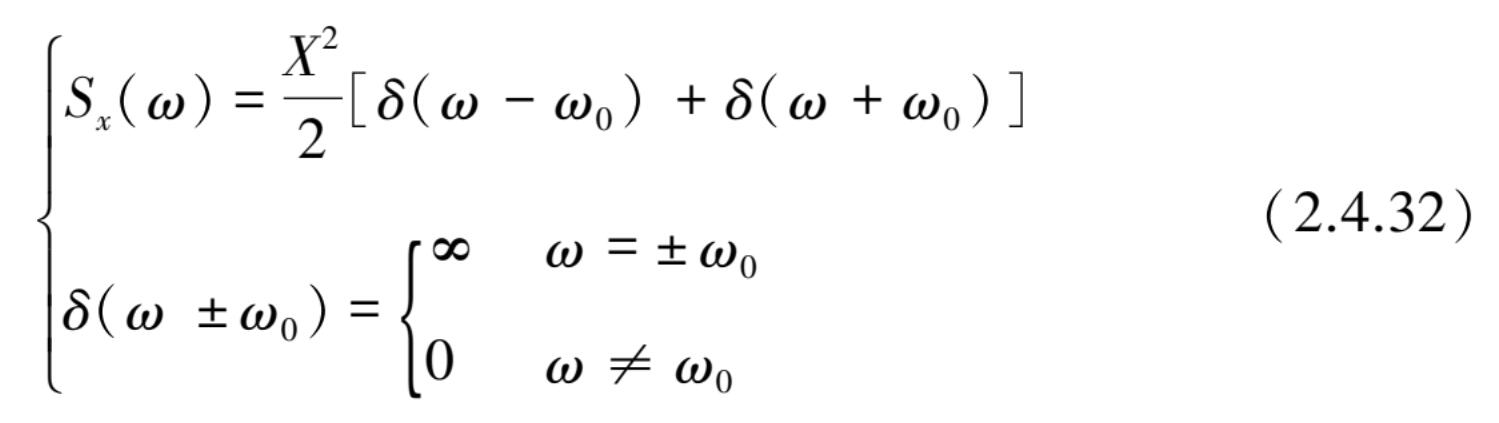
在
ω
=0~∞范围的
S
x
(
ω
)积分的均方值为
 。
。
图 2.4.7(d)所示的功率谱密度曲线比较宽,也比较平滑,这也是取“宽带”这名词的实质依据。如果是白噪声,则 S x ( ω )=常数,即在整个 ω 区域上是均匀分布的。
图 2.4.7(b)表示简单正弦波加随机噪声的功率谱密度函数相加的 S x ( ω )。
图 2.4.7(c)表示窄带噪声功率谱密度函数,具有正弦波的那种尖峰,但又相似于随机噪声那样平滑过渡。
图 2.4.7 所示的 4 个例子再次表明从正弦波到宽带随机噪声的功率谱密度函数具有明显变化的趋势。
功率谱密度函数很重要的用途是用来建立数据信号的频率特性。如振动系统反应的传递函数为 H (j ω )时,假设输入是一个平稳随机信号的 S x ( ω ),则振动系统的反应输出也将是一个平稳随机信号的 S y ( ω )。