




如 2.2 节所述,对于随机现象的数据不能用精确的数学关系式描述。如图 2.3.1 所示,某随机数据不同时刻的样本记录是不相同的。
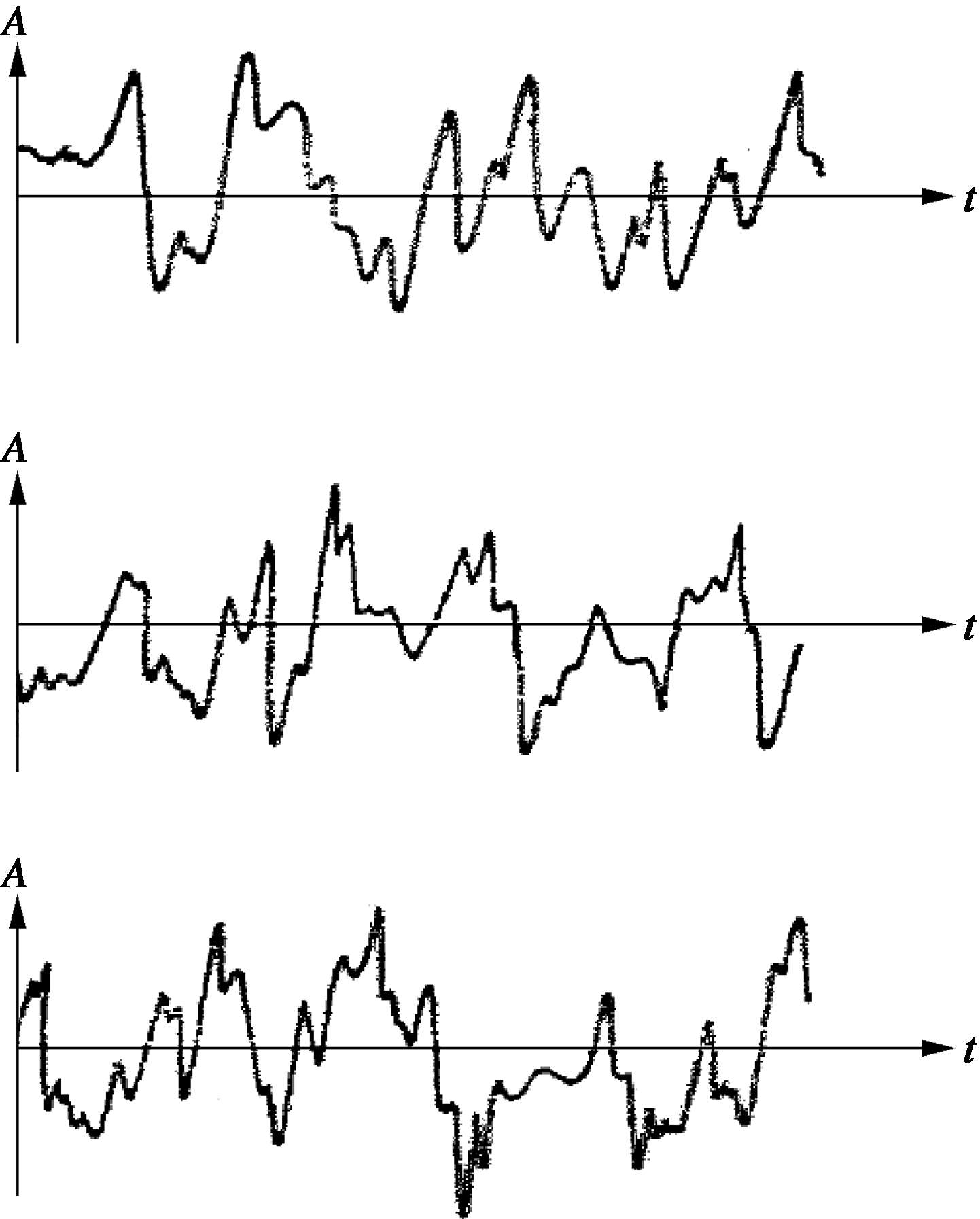
图2.3.1 随机数据不同时刻的样本记录曲线
表征随机现象的单个时间历程,被称为样本函数。在有限时间区间上观察,被称为样本记录。随机现象可能产生的全部样本函数的集合被称为随机过程。因此,随机物理现象的一个样本记录可以认为是该随机过程的一个物理现象。
随机过程一般分为平稳和非平稳两类,平稳随机过程又可分为各态历经和非各态历经两种,非平稳随机过程按非平稳特性分成特殊的种类,如图 2.3.2 所示。
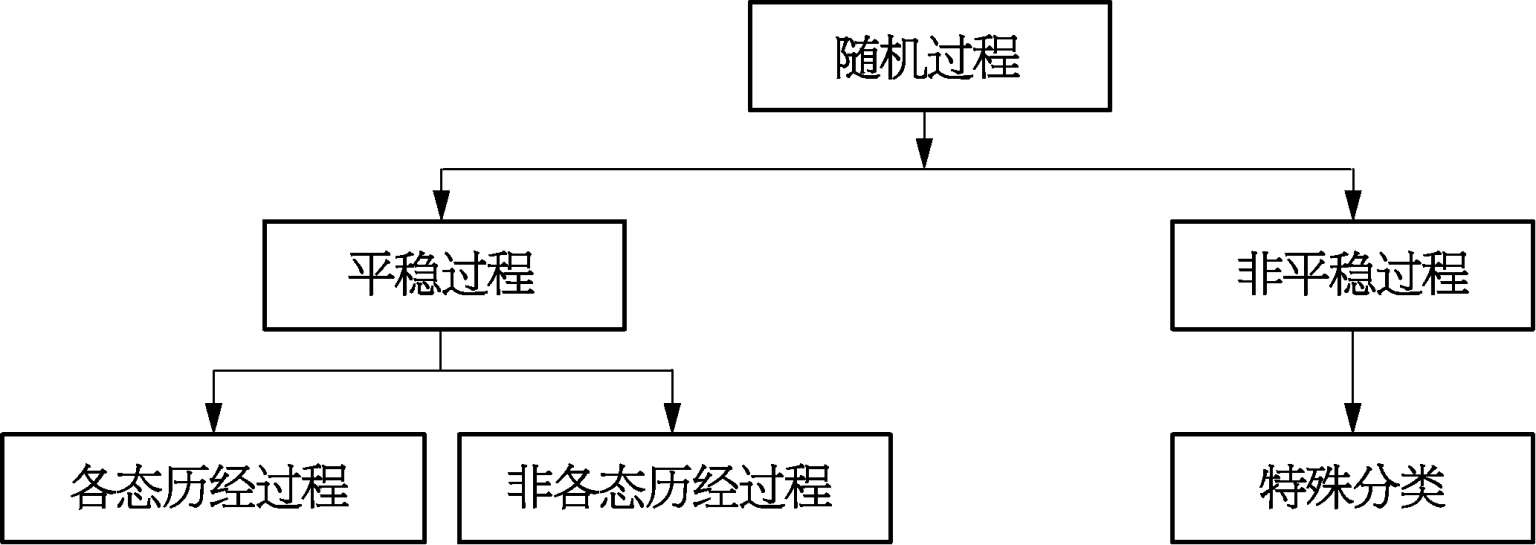
图2.3.2 随机数据的分类
当任何时刻 t 的特性可以用随机过程样本函数集合的平均值来描述时则可定义为平稳随机过程。
例如,由图 2.3.3 所示随机过程的样本函数集合(通常也称为总体),随机过程在某一时刻 t 1 上的均值(一阶矩),可以将 t 1 总体中各个样本函数的瞬时值相加,然后除以样本函数的个数而获得总体平均值。类似的对随机过程两个不同时刻之值的相关性(二阶矩),可由 t 1 和( t 1 + τ )两时刻值乘积的总体平均获得,这样随机过程{ x ( t )}用均值 μ x ( t 1 )和自相关函数 R x ( t 1 , t 1 + τ )来表示,其数学表达式为
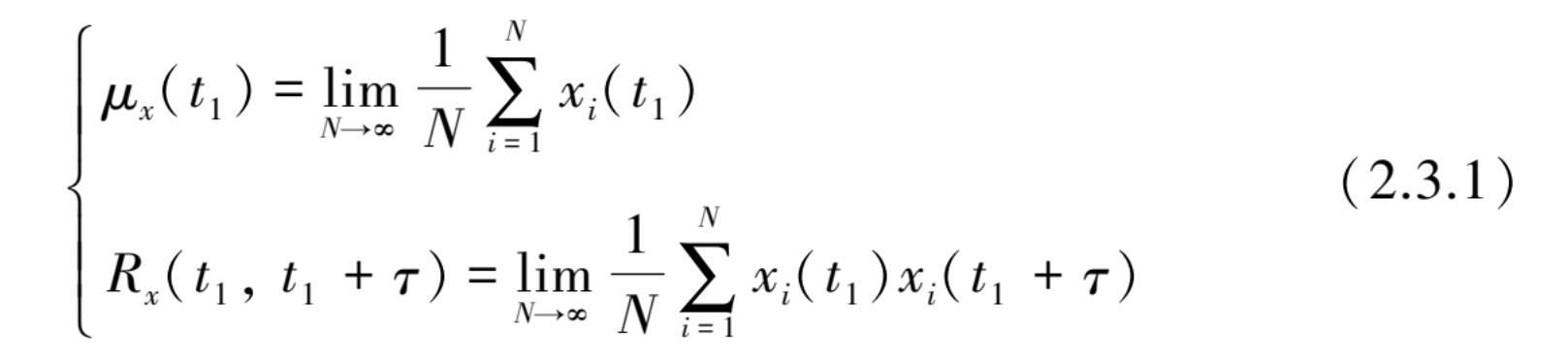
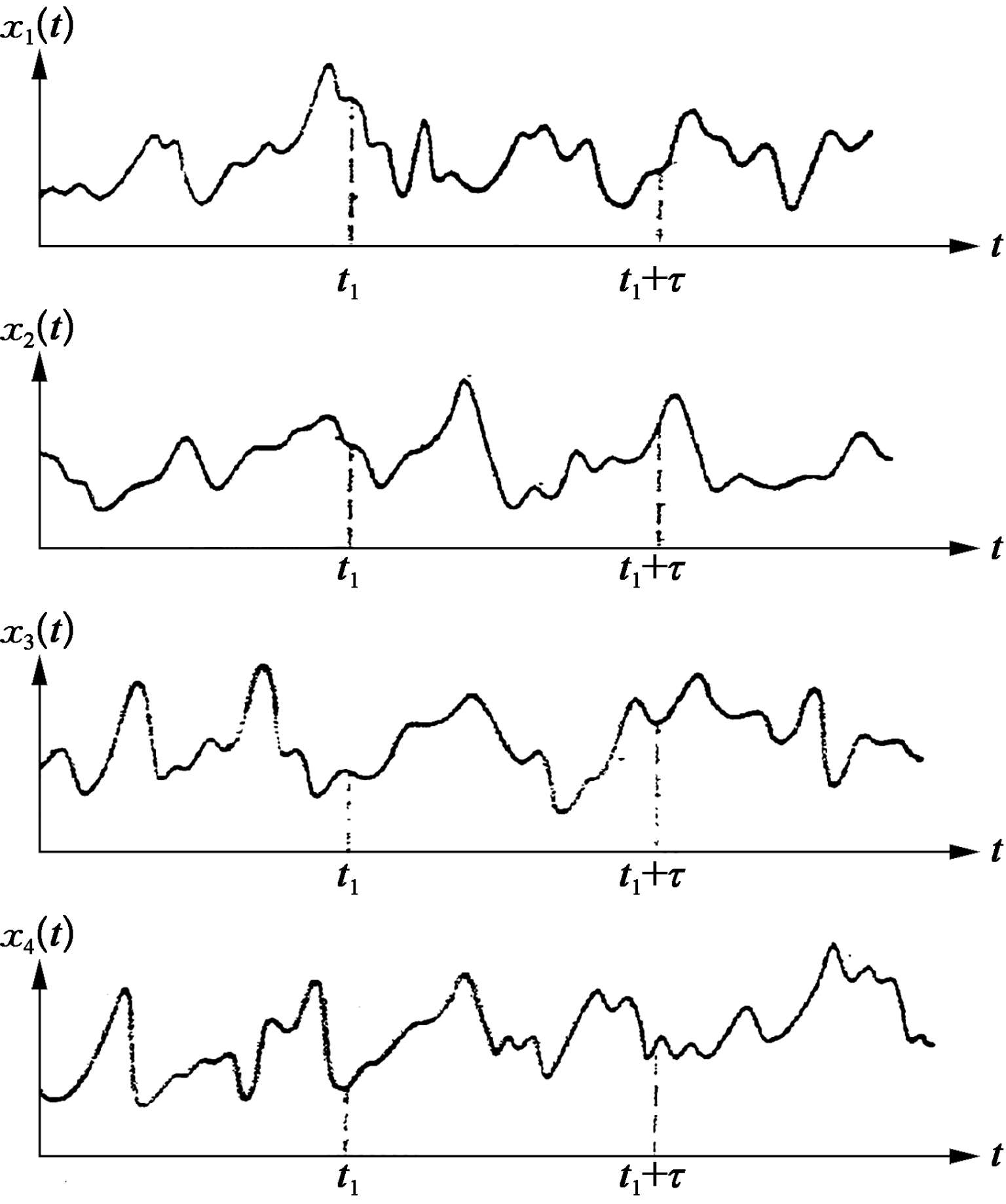
图2.3.3 随机过程的样本函数取总体平均
通常情况下,式(2.3.1)中 μ x ( t 1 )和 R x ( t 1 , t 1 + τ )是随时刻t的改变而改变的,该随机过程{ x ( t )}称为非平稳的样本函数。只有在特定情况下,当 μ x ( t 1 )和 R x ( t 1 , t 1 + τ )不随 t 1 变化时,则该随机过程{ x ( t )}称为平稳的样本函数,这时对于平稳随机过程的均值 μ x ( t 1 )= μ x 是常数,自相关函数 R x ( t 1 , t 1 + τ )= R x ( τ )只与相关时间 τ (或称时间位移)有关。
为了得到描述随机过程的总体概率分布函数,需要计算随机过程{ x ( t )}中无限个高阶矩和联合矩。当所有的矩和联合矩均不随时间变化时,则称该随机过程{ x ( t )}为强平稳,或是严格平稳。在许多实际应用中,若能够证明该过程为弱平稳性时,往往也可近似归入强平稳随机过程。
2.3.1 节专门讨论了如何用具体时刻上的总体平均来确定随机过程中的一些统计特性。但是,大多数情况下,也可以用总体中取出某样本函数的时间平均来确定平稳随机过程的统计特性。
例如,图 2.3.3 所示随机过程中相应的样本函数,其均值 μ x ( k )和自相关函数 R x ( τ ,k)分别为
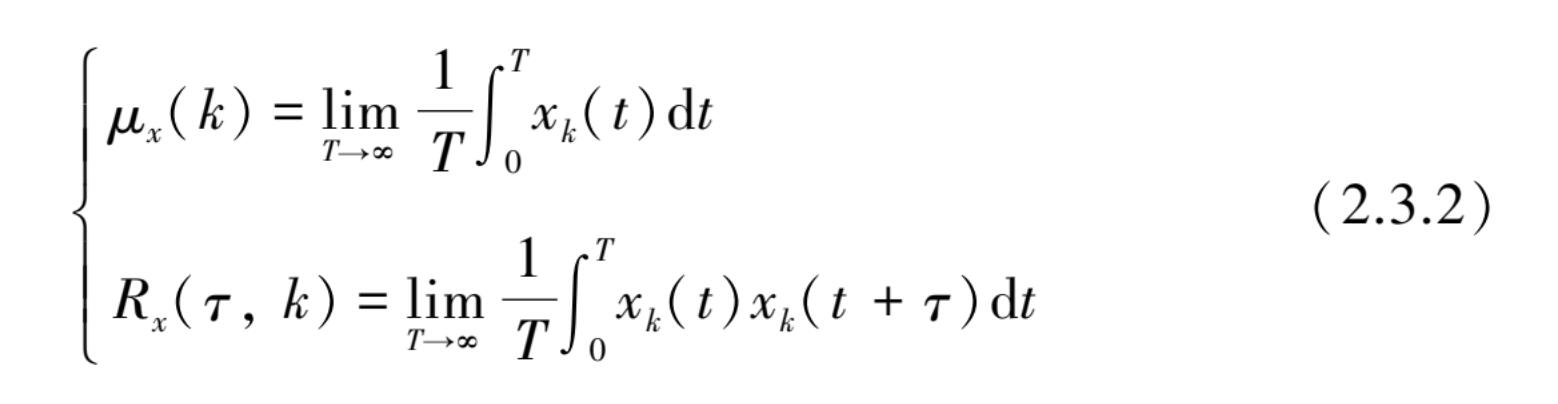
如果随机过程{ x ( t )}是平稳的,而且采用不同样本函数计算式(2.3.2)所得到的 μ x ( k )和 R x ( τ , k )的值都一样时,则称该随机过程为各态历经的。对于各态历经的随机过程,按时间平均的均值 μ x 和自相关函数 R x ( τ )将等于相应的随机过程总体平均值,即
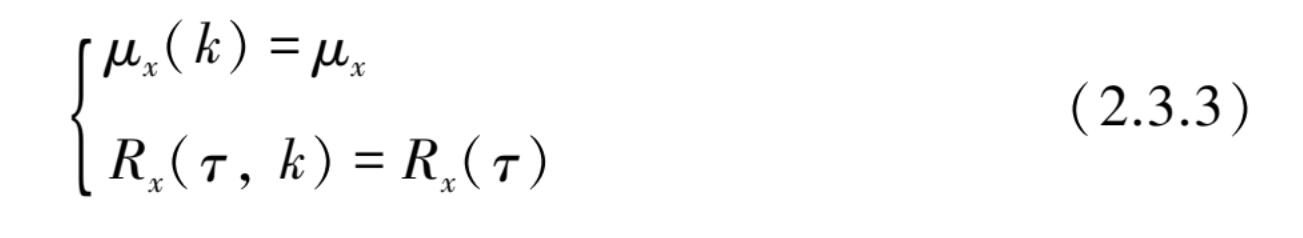
应注意的是,只有平稳随机过程才可能是平稳的,反之也说明各态历经必然是一种平稳随机过程。也就是说,各态历经是平稳随机过程的充分必要条件。
各态历经随机过程的所有统计特性可以用单个样本函数上的时间平均来描述,因此,各态历经随机过程显然是随机过程中很重要的一类。大量实践表明,平稳物理现象的随机现象大多数属于各态历经的,为此都可以用单个观察到的时间历程记录来测定平稳随机现象的统计特性。
非平稳随机过程包括所有不满足 2.3.1 节中关于平稳特性要求的随机过程。非平稳随机过程的特性通常是统计值随时间而变化,它只能用随机过程中样本函数的总体瞬时平均来确定。在实际中很不易获取非平稳随机过程足够数量的样本记录来精确测量其总体平均的统计特性。
在很多情况中,许多物理现象所产生的非平稳数据,可以进一步分解为一系列的特殊类别,以便简化测量和分析方法。例如,某些随机数据可以采用样本函数 y ( t )来描述非平稳随机过程:

式中, x ( t )为平稳随机过程{ x ( t )}的样本函数, A ( t )为一个确定性乘法因子(或称为加权系数)。这类数据可以用一个具有共同确定性时间趋势的样本函数组成的非平稳随机过程来表征。如果该非平稳随机数据可以用这一类模型拟合时,则描述该类数据就不一定要用总体平均。有时可与各态历经平稳数据类似,用单个样本记录估计各种需要的统计特性,如模拟地震加速度波时间历程常用非平稳随机过程模型 f ( t )来表征:

式中, g ( t )为时间 t 的确定性函数, x ( t )为平均值为 0 的平稳高斯随机过程函数。
2.3.1 节所讨论和定义的平稳性概念是指随机过程的总体平均特性而言的,但在实践中通常称随机现象的单个时间历程记录数据为平稳或非平稳的。
为了帮助理解,考虑单个样本记录{ x k ( t )},它由随机过程{ x ( t )}中相应于k的样本函数得到。假定在短时间区间 T 上按时间加以平均,设起始时间为 t 1 所得到的均值和自相关函数为
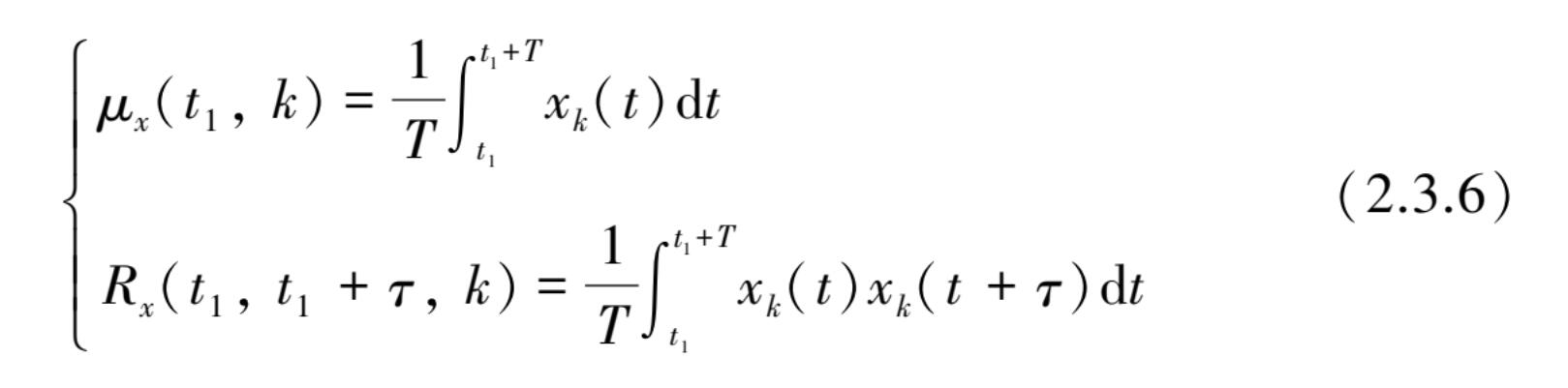
通常情况下,若式(2.3.6)所确定样本记录的性质是随起始时间 t 1 的变化而有明显变化时,此时就称单个样本记录为非平稳的。只有在特定情况下,式(2.3.6)所定义的样本记录的性质不随 t 1 的变化而有明显的变化时,则称此样本记录是平稳的。因此如果假设在各态历经条件下,只需验证“单个样本”所记录的平稳性即可有效地认为此记录所在的随机过程能满足平稳性和各态历经。式(2.3.3)中,当 μ x 和 R x 与 t 1 无关时,属于平稳性质;当与 k 无关时,则属于各态历经的,只有是平稳随机过程才有可能存在各态历经。