




一般确定性的物理现象数据,可分为周期的和非周期的两类,周期数据可进一步分解为正弦周期数据和复杂周期数据两类;非周期数据可以进一步分为准周期和瞬时两类。图 2.2.1 为确定性数据如何分类的路径图。
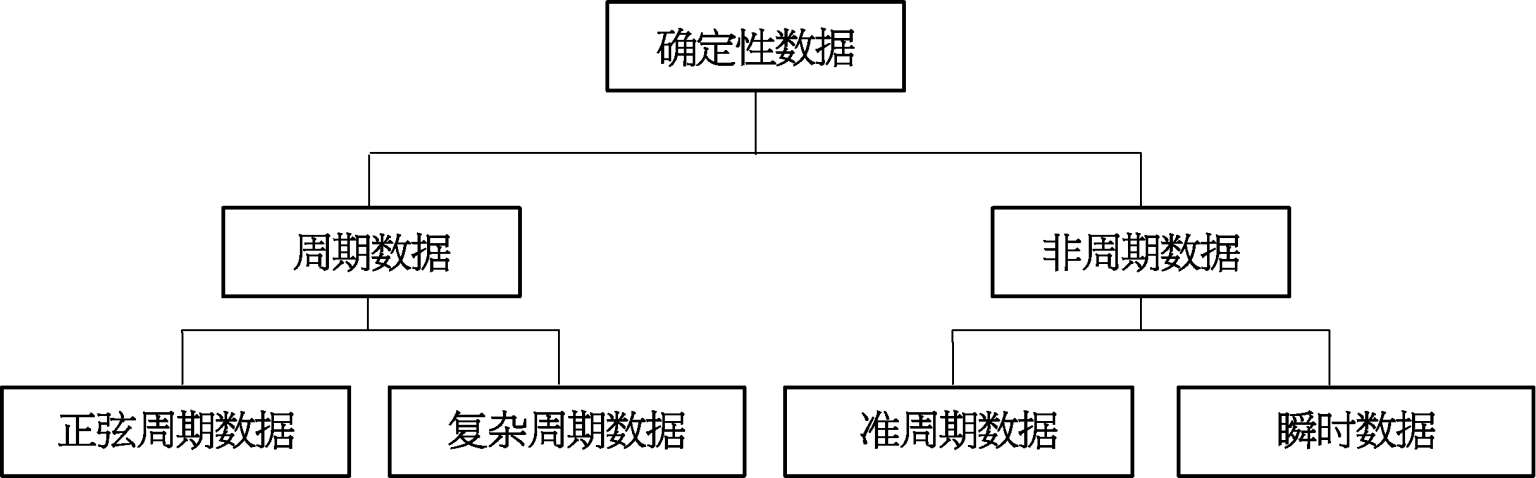
图2.2.1 确定性数据的分类
正弦波数据可用时程函数表示为

式中, X 为正弦波幅值, ω 0 为圆频率。式(2.2.1)可用时程图或频谱图加以描述。
正弦曲线完成一个循环周期所需的时间称为周期 T 0 ,在单位时间内的循环数称为频率 f 0 ,两者关系为

图 2.2.2 的频谱图由单一频率 ω 0 (或 f 0 )上的幅值 X 组成,这种频谱相对于连续谱而言称为“离散谱”或“线谱”。
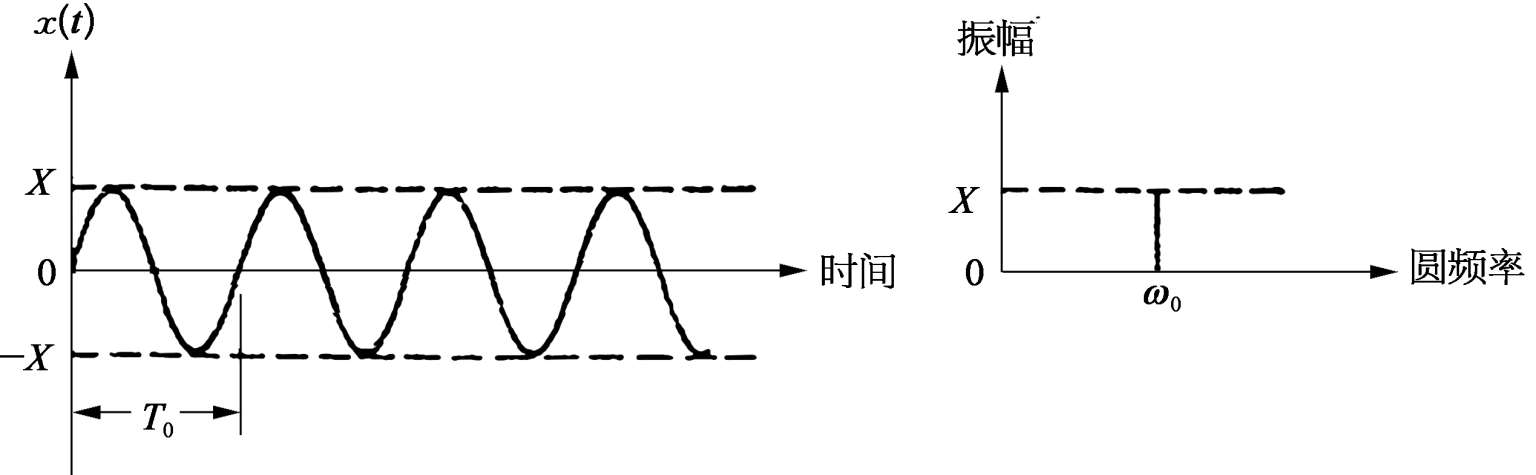
图2.2.2 正弦数据的时程和频谱
实际振动中会形成近似的正弦波数据,是时变数据中最简易的形式。
复杂周期数据能用周期性时间变化函数表示为
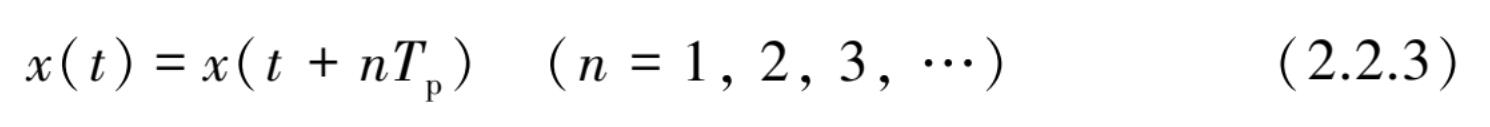
该函数具有基波的整数倍所组成的波形,与正弦数据相同,其中 T p 为一个循环的周期时间,单位时间内的循环数称为“基频 ω 1 ( ω 1 =2π f 1 )”,显然,正弦数据是复杂周期数据在 f 1 = f 0 时的一个特例。
复杂周期数据均可以将 x ( t )展开成傅里叶级数:
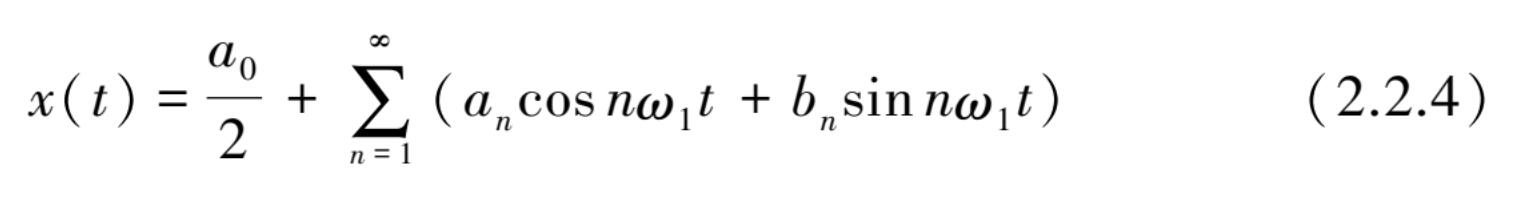
式中,
 =
=
 =
=
 ,系数
,系数
 =
=
 ,
,
 =
=
 ,
,
 =
=
 (
n
=1,2,3,…)。
(
n
=1,2,3,…)。
式(2.2.4)可用幅值和相位角的另一种形式来表示:
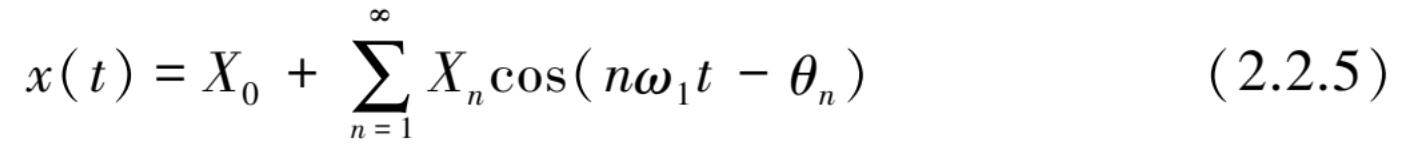
式中,
 =
=
 ,
,
 =
=
 ,
,
 =
=
 。
。
a 0 表示一个非周期性的并在频域上为 0 频率的分量,是常数静态项,对动态曲线而言可以被忽略。对式(2.2.5)可以用图 2.2.3 所示的离散谱来表征。这里要注意,对于复杂周期数据有时只包含几个分量,有时基本分量也可没有。例如某周期函数 x ( t )只包含 60,75,100 Hz,它们的最高公约数为 5,故这合成的周期数 T p =0.2 s,即 f 1 =5 Hz,因此展开傅里叶级数时,除 n =12,15,20 这 3 项以外,所有 X n 值均为零。
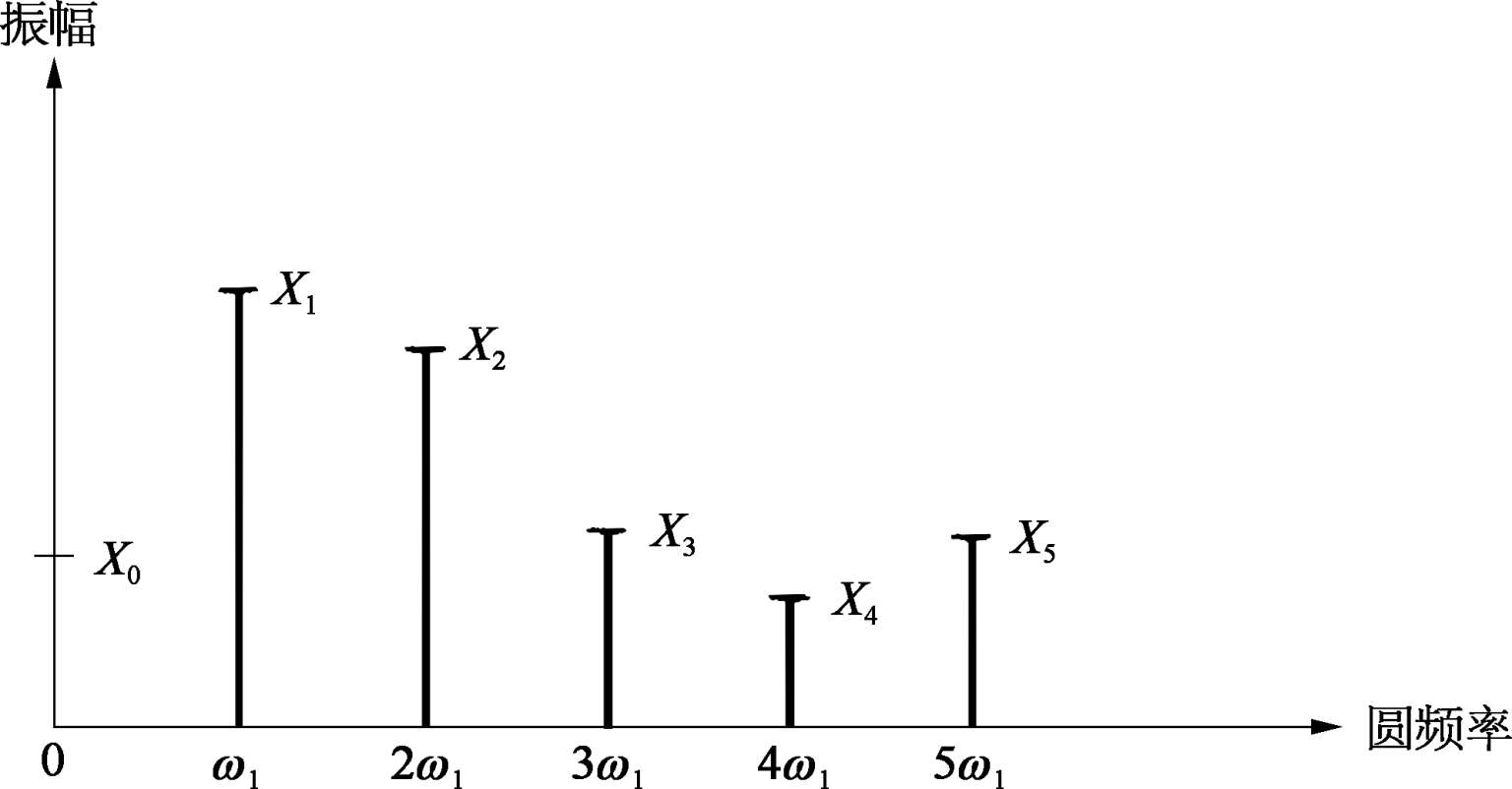
图2.2.3 复杂周期数据谱
本书附录E专门阐述了某些复杂周期函数怎么应用三角级数模型方法。
如 2.2.2 节所述,周期数据一般可以简化成一系列频率成比例的正弦波。反过来,两个或几个频率成比例的正弦波叠加在一起将组合成一个周期数据。但要注意任意频率的两个或几个正弦波之和通常不会形成周期数据,具体来说,只有当每一对频率之比为有理数时,两个或几个正弦波之和才会形成周期数据。如
x ( t )= X 1 si n (2 t + θ 1 )+ X 2 si n (3 t + θ 2 )+ X 3 si n (7 t + θ 3 )
因基本周期 T P =1, ω 1 / ω 2 =2 /3, ω 1 / ω 3 =2 /7, ω 2 / ω 3 =3 /7 均为有理数,所以 x ( t )应为周期性的。
对于
x
(
t
)=
X
1
si
n
(2
t
+
θ
1
)+
X
2
si
n
(3
t
+
θ
2
)+
X
3
si
n
(
 t
+
θ
3
)
t
+
θ
3
)
则不是周期性的,因为
ω
1
/
ω
3
=2 /
 ,
ω
2
/
ω
3
=3 /
,
ω
2
/
ω
3
=3 /
 不是有理数,称该函数的时间历程具有“准周期”特性。
不是有理数,称该函数的时间历程具有“准周期”特性。
准周期数据是一种非周期数据,可用交变函数表示为
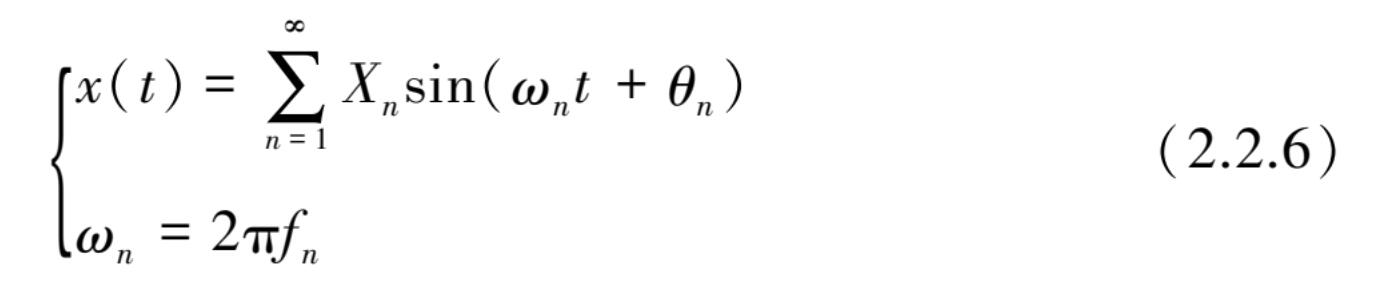
ω n / ω m ( f n / f m )在任何情况下均不是有理数。对准周期数据的一个重要性质是,假设式(2.2.6)中的相位角 θ n 可以忽略时,则 x ( t )可用如图 2.2.4 所示的离散谱来表示。这与处理那些复杂周期性数据类似,其差异仅在于各分量对应的频率不再是有理数比例关系。
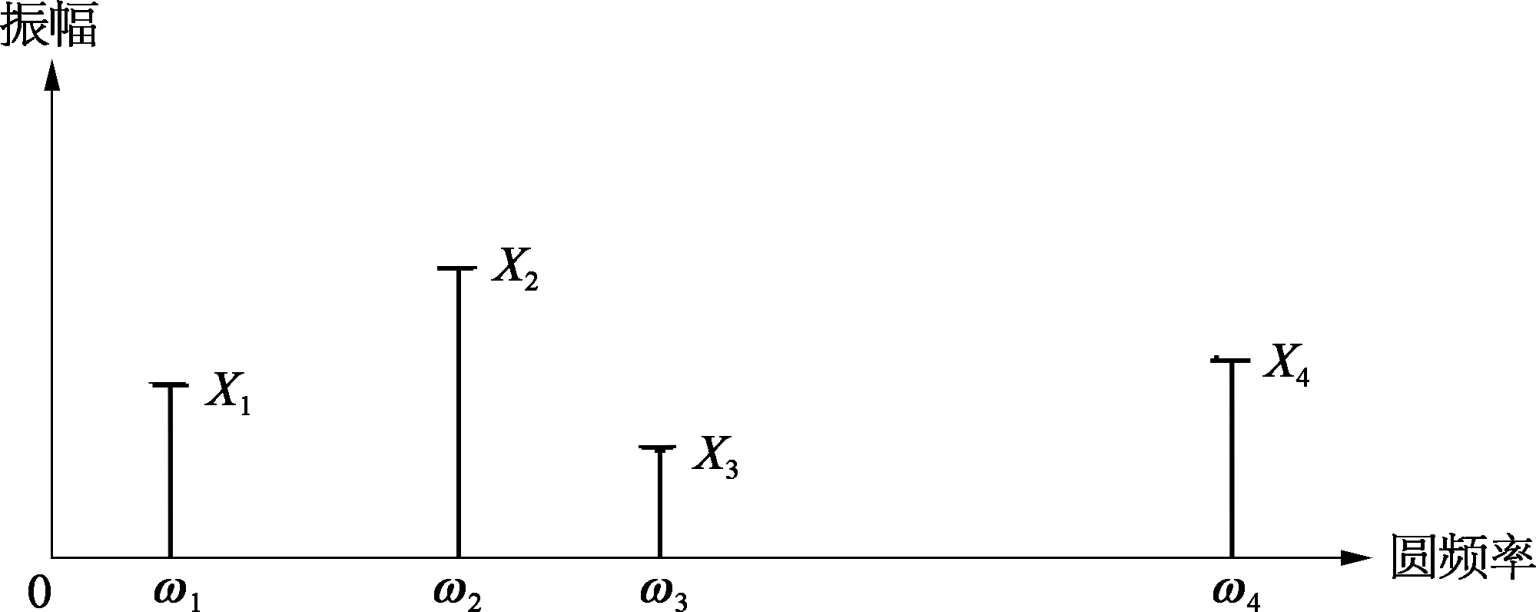
图2.2.4 准周期数据谱
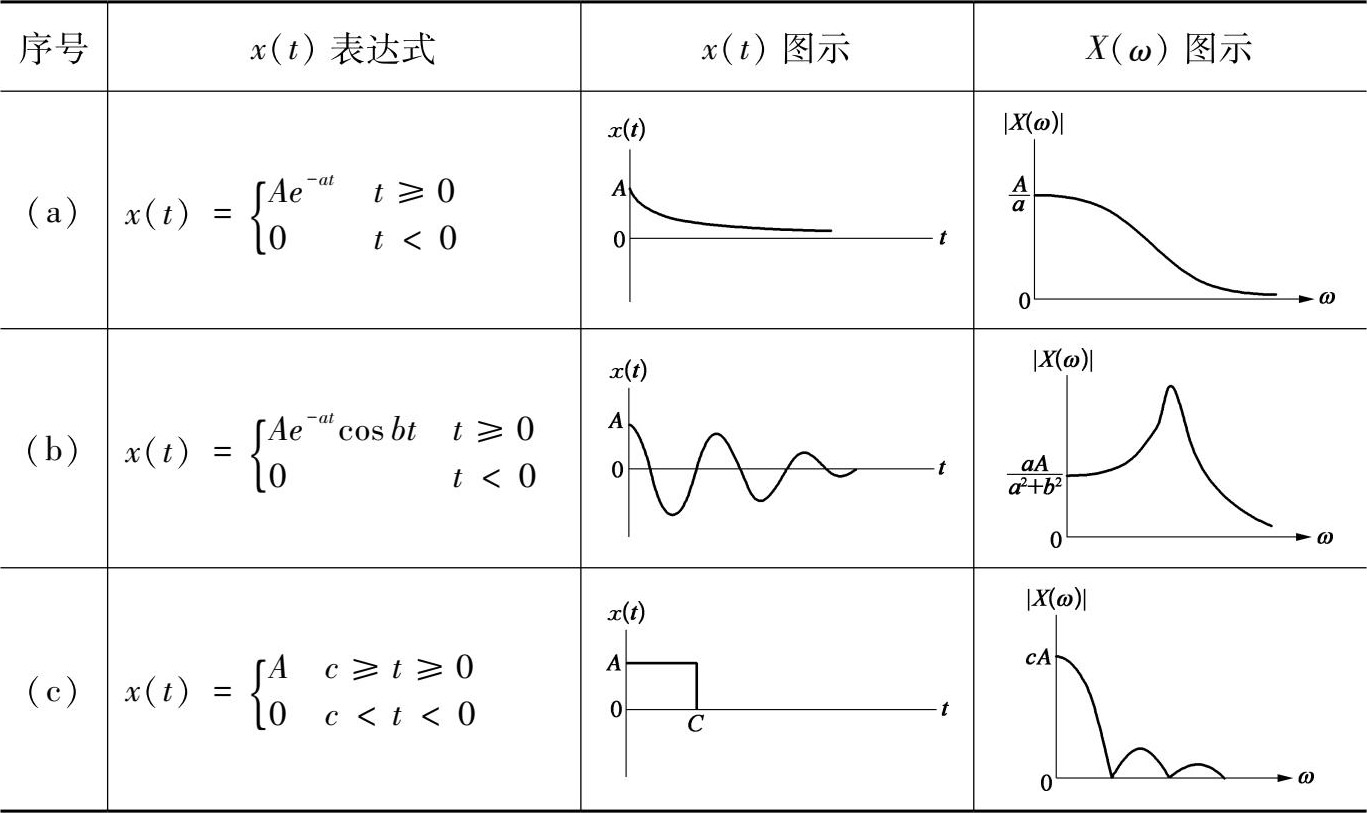
瞬时数据属于除 2.2.3 节所述的准周期数据以外的非周期数据。表 2.2.1 给出了瞬时数据的 3 个简单例子。
表2.2.1 瞬时数据特例
非周期数据与周期、准周期数据不同,其中一个很重要特征是其函数不能采用离散谱来表征,但可以用傅里叶积分变换方法来表征连续谱:
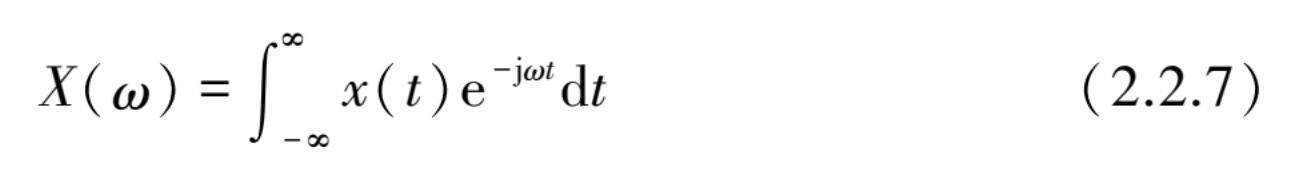
其逆变换表达为
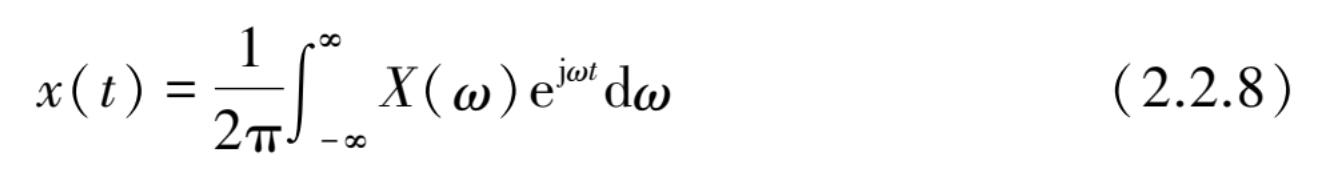
傅里叶谱 X ( ω )是一个复数,可用幅值| X ( ω )|与幅角 θ ( ω )表示为
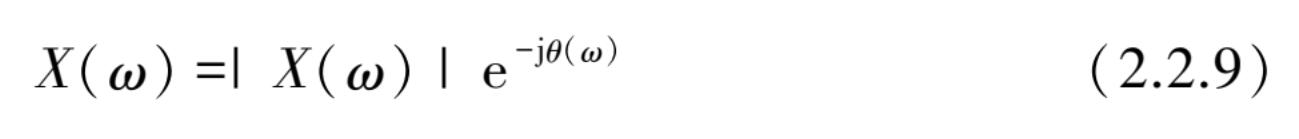
表 2.2.1 给出了 3 个瞬时时间历程对立的傅里叶谱, X ( ω )的幅值用| X ( ω )|来表示。