第Ⅲ卷　问题5-21

5.求三个数使它们的和为平方数，且其中任意一对的和都大于第三个某一个平方数。

设三个数的和是（x+1） ² ；令第一个+第二个=第三个+1，则第三个= ；

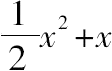令第二个+第三个=第一个+x ² ，则第一个=

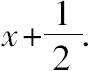
从而第二个=

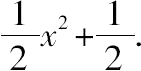
另外还有，第一个+第三个=第二个+平方数。

从而2x=平方数，不妨说=16，得x=8。

所求数为 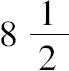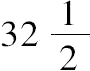， ，40。

另外一种解法如下 ^[1] 。

首先求三个平方数，使其和仍是平方数。例如求一个平方数+4+9仍是平方数，而36恰好适合；因此，4，36，9是具有所要求特性的平方数。

下一步求三个数，使其中任一对数的和=第三个+所给定的数；

在此情况下，假设

第一+第二-第三=4，

第二+第三-第一=9，

第三+第一-第二=36。

此题已解［卷Ⅰ，18］，

所求数依次为20， ， 。

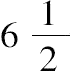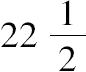从而

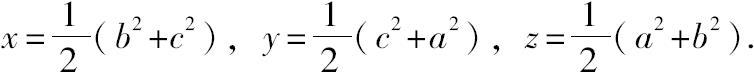
6.求三个数，使它们的和是平方数，且其中任意一对的和也是平方数。

令三个数之和为x ² +2x+1，第一，第二之和为x ² ，因此第三个为2x+1；

令第二，第三之和为（x-1） ² ，因此第一个=4x，第二个=x ² -4x。

但是，第一个+第三个=平方数，即6x+1=平方数，不妨说=121。

从而x=20，且

所求数为80，320，41。

[此处有一个替换解，明显是后来插入的。因为它本质上是一样的，不同的是取6x+1的值为36，从而x=35/6，且所求数为840/36，385/36，456/36。]

7.求三个成等差的数，使其中任意一对的和均为平方数。

首先求三个成等差的平方数，使其和的一半大于其中任一个数。

令其中第一个，第二个为x ² ，（x+1） ² ；

则第三个为x ² +4x+2=（x-8） ² ，不妨说。

因此x=62/20或31/10；

从而可取三个平方数为961，1681，2401。

现在求三个数，使其中任意一对的和恰好等于所求出的数。

这三个数的和=5043/2= 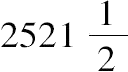，且

这三个数是 ， ，

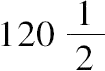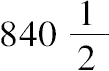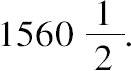
8.给定一个数，求另外三个数使其中任意一对的和加上此给定数均为平方数，且这三个数的和加此给定数也为平方数。

给定数为3。

设所求的第一个+第二个=x ² +4x+1，

第二个+第三个=x ² +6x+6，

三个数的和=x ² +8x+13。

从而第三个=4x+12，第二个=x ² +2x-6，第一个=2x+7。

还有　第一个+第三个+3=平方数，

即，　6x+22=平方数，不妨说=100。

因此　x=13，且

所求数为33，189，64

9.给定一个数，求另外三个数使其中任意一对的和减去此给定数均为平方数，且这三个数的和减此给定数也为平方数。

给定数为3。

设所求数的　第一个+第二个=x ² +3，

第二个+第三个=x ² +2x+4，

三个数的和=x ² +4x+7。

从而第三个=4x+4，第二个=x ² -2x，第一个=2x+3。

最后，第一个+第三个-3=6x+4=平方数，不妨说=64。

因此　x=10，且

（23，80，44）是一组解。

10.求三个数，使其中任意一对之积加上一给定数均为平方数。

设给定数是12。取一平方数比如25，并减去12，把差13作为第一，第二两数之积，

并设这两数分别为13x，1/x。

再从另一平方数比如16中减去12，并把差4作为第二，第三两数之积。

因此第三个数=4x。

第三个条件要求52x ² +12=平方数；这里52=4·13，其中13不是平方数；

但是，如果13是平方数，这个方程就容易解了。 ^[2]

因此必须找两个数以取代13和4，满足它们的积为平方数，

而其中任何一个数+12也是平方数。

如果两个数均为平方数，则二者之积也是平方数，因此必须找两个平方数，

使其中任何一个+12=平方数。

“按以前讲过的方法，这是容易做到的 ^[3] ，并且它可使方程容易解出。”

平方数4，1/4满足这一条件。

返回前面的步骤，现在设所求的三个数为4x，1/x和x/4。在此情况下，要解方程x ² +12=平方数，不妨设=（x+3） ² 。

所以x=1/2。于是（2，2，1/8）是一组解。 ^[4]

11.求三个数，使其中任意一对之积减去一给定数均为平方数。

设给定数是10。

取第一和第二之积=平方数+10，不妨说=4+10，并令第一=14x，第二=1/x。

取第二和第三之积=平方数+10，不妨说=19；

因此，第三=19x。

由第三个条件，266x ² -10必须是平方数，但266不是平方数 ^[5] 。

因此，同上题一样，必须求两个平方数，使其中任何一个=平方数+10。

而平方数 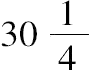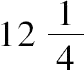， 满足这些条件 ^[6] 。

现令所求数为 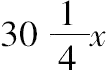，1/x， ，

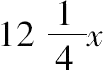由第三个条件可得 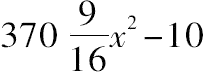=平方数

[其中丢番图把 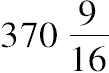记为 ]；

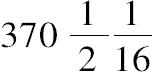因此5929x ² -160=平方数，不妨说=（77x-2） ² ，从而x=41/77。

所求数为

12.求三个数，使其中任意两个之积加上第三个均为平方数。

取一个平方数并减去其中一部分作为第三个数；

如令x ² +6x+9是其中一平方数，且9是第三个数。

因此第一和第二之积=x ² +6x；若取第一=x，则第二=x+6。

由另两个条件知

因此必须求两个平方数其差为48；“这是容易的，且方法很多”。

平方数16，64就满足此条件。令其等于相应表达式，可得x=1，且

所求数为1，7，9。

13.求三个数，使其中任意两个之积 减去 第三个均为平方数。

令第一为x，第二为x+4；则其乘积=x ² +4x，因此可设第三为4x。

从而由其他条件知

而其差=16x+4=4（4x+1），

若令 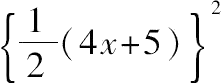=4x ² +15x从而x=25/20，且

所求数为25/20，105/20，100/20。

14.求三个数，使其中任意两个之积加上第三个的平方，均为平方数 ^[7] 。

设第一个为x，第二个为4x+4，第三个为1。

则两个条件已经满足。

第三个条件是

x+（4x+4） ² =平方数，不妨说=（4x-5） ² ，

因此x=9/73，且

所求数（省略公分母）为9，328，73

15.求三个数，使其中任意两个之积加上该两个之和均为平方数。 ^[8]

［引理］任意两相邻数的平方的乘积，加上这两相邻数的平方的和，仍是平方数 ^[9] 。

令4，9为所求的两个数，x为第三个数。

因此 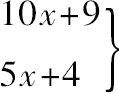必须都是平方数。

其差=5x+5=5（x+1）.

让两因子的和的一半的平方等于10x+9，

得 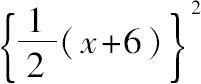=10x+9。

从而x=28，且（4，9，28）是一组解。

另一种解法 ^[10] 。

设第一个数为x，第二个为3。

因此4x+3=平方数，不妨说=25，

从而x= 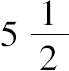，且 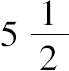，3满足一个条件。

令第三个是x，而前两个是 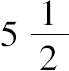，3。

因此 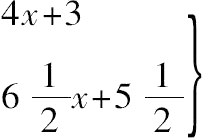必须都是平方数。

但是，这是不可能的。因为相应的系数没有一对的比率是平方数与平方数的比率。

为了用平方数与平方数的比率作系数替代 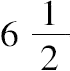，4，因此寻求两个数来替代 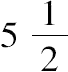，3，使其满足它两的积加上它两的和等于平方数，且它两各加上1后其比率为平方数比平方数。

为此令y和4y+3为这两数，显然满足第二个条件，为了第一个条件，必须让

4y ² +8y+3=平方数，不妨说=（2y-3） ² 。从而y=3/10。

在解出3/10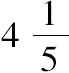， 后，进一步假设第三个数为x，

因此 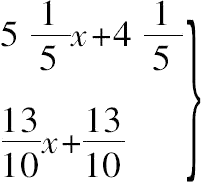都必须是平方数或者在依次乘以25和100之后 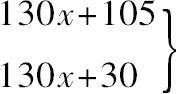都必须是平方数，

其差75=3·25，由通常的解法可知x=7/10，

因此所求数为3/10，42/10，7/10。

16.求三个数，使其中任意两个之积减去该两数之和均为平方数。

如果令第一个数为x，第二个数任意取值，那么会和上题一样出现相同的困难。

因此，必须寻求两个数，满足

（a）它们的乘积-它们的和=平方数，且

（b）各自减去1后，剩余部分具有平方数的比率。

显然4y+1和y+1满足后一条件。

而公式（a）要求

4y ² -1=平方数，不妨说=（2y-2） ² ，

可得y=5/8，在得出13/8，28/8之后，然后令第三个为x，

因此 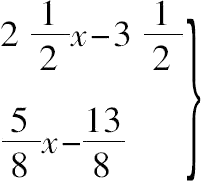必须都是平方数。

或者依次乘以4，16，

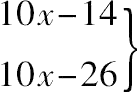必须都是平方数。

其差12=2·6，用通常方法可得x=3，

因此所求数为13/8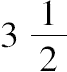， =28/8，3=24/8。

17.求两个数，使其乘积加上每一个数以及两数之和，均为平方数。

假设所求数为x，4x-1，因为x（4x-1）+x=4x ² 都是平方数。

因此还有

其差x= 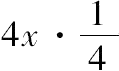，可求出　x=65/224。

所求数为65/224，36/224。

18.求两个数，使其乘积减去每一个数以及两数之和，均为平方数。 ^[11]

假设所求数为x+1，4x，因为4x（x+1）-4x=平方数。

因此还有 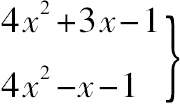必须都是平方数。

其差4x=4x·1，可得x= 。

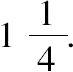所求数为 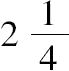，5。

19.求四个数，使其和的平方加上或减去任一单个数均为平方数。

因为在直角三角形中，

斜边的平方±2×两直角边的乘积=平方数，

因此必须求出四个具有相同斜边的直角三角形［在有理数范围］；

换句话，必须求一平方数，它可分为四组两个平方数之和。且“我们已经知道，将一平方数分为两平方数之和，其方式可以有任意多种。”［卷Ⅱ，8题］

取两个较小的直角三角形（3，4，5）和（5，12，13）；

给每个三角形的各边乘以另一三角形的斜边，则可得到两个具有相同斜边的有理直角三角形（39，52，65）和（25，60，65），从而65 ² 已分为两组两个平方数之和。

另外，由于65=13·5，且13=2 ² +3 ² ，5=1 ² +2 ² ，

所以65可分成两组两个平方数之和，亦即7 ² +4 ² 和8 ² +1 ² 。

现在由7，4构造直角三角形 ^[12] ，其边为（7 ² -4 ² ，2·7·4，7 ² +4 ² ）或（33，56，65）。

类似地，有8，1构造直角三角形，可得（2·8·1，8 ² -1 ² ，8 ² +1 ² ）或（16，63，65）。

总之，65 ² 已分成四组两个平方数之和。

现在假设四个数之和为65x，且

第一个数为2·39·52x ² =4056x ² ，

第二个数为2·25·60x ² =3000x ²

第三个数为2·33·56x ² =3696x ² ，

第四个数为2·16·63x ² =2016x ² ，

以上x ² 的系数依次是四个直角三角形的面积的四倍。

其和12768x ² =65x，且x=65/12768。

所求数是 ， ， ，

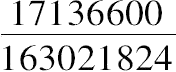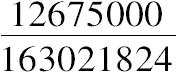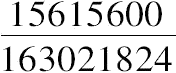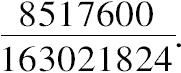
20.将一给定数分为两部分，并求一平方数，使其减去该两部分均为平方数 。

给定数10，所求数为x ² +2x+1。取一部分为2x+1，另一部分为4x。

如果6x+1=10，那么条件都成立。

因此x=

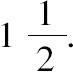
两部分为（4，6），平方数为

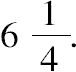
21.将一给定数分为两部分，并求一平方数，使其加上该两部分均为平方数。

给定数为20，所求平方数为x ² +2x+1。

如果此平方数加上2x+3或者4x+8，结果仍是平方数。

因此取2x+3，4x+8为20的两部分，从而6x+11=20，x=

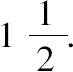
因此，两部分为（6，14），平方数为

---

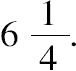
[1] 可能像其他题的第二种解法一样，有人习惯性认为此替换解是后来插入的。但此解法如此巧妙，我们很难归功于后来的评注者。丢番图的解法通常都是可想到的最佳方法，此题不该例外。事实上，此替换解更优美，可以一般化为如下过程：欲求x，y，z，使

-x+y+z=平方数

x-y+z=平方数

x+y-z=平方数

x+y+z=平方数

令前三个表达式分别为平方数a ² ，b ² ，c ² ，且满足a ² +b ² +c ² 也必须是平方数，不妨记为k ² 。

[2] 事实上，方程52x ² +12=u ² 是可解的，明显x=1是一个解。亦可用y+1替代x，找到其他解，等等。而x=1本身就可得到此题的解（13，1，4）。

[3] 此方法见卷Ⅱ，34题。需要求两对平方数，其差都是12。

（a）如果令12=6·2，有

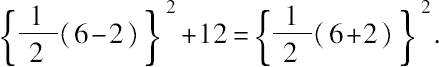
16，4就是相差12的平方数，换句话说，4就是一个平方数，其加12也是平方数。

（b）如果令12=4·3，可求出

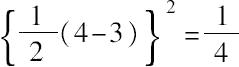就是一个平方数，其加12也是平方数。

[4] 欧拉（Algebra，Part Ⅱ.Art.232）对此题的一般解给出了一个优美的解法。求x，y，z，使xy+a，yz+a，zx+a都是平方数。

设xy+a=p ² ，并令z=x+y+q；

因此xz+a=x ² +xy+qx+a=x ² +qx+p ² ，

且yz+a=xy+y ² +qy+a=y ² +qy+p ² ；

如果q=±2p，则右边表达式全为平方数，故取z=x+y±2p.

从而p可取任意的值，只要满足p ² ＞a，将p ² -a分解为两因子，依次取为x，y的值，

z可得。

例如设a=12且p ² =25，则xy=13；

让x=1，y=13，则z=14±10=24或4，

故解为（1，13，4），（1，13，24）。

[5] 其实，方程266x ² -10=u ² 本身是可解的，因为x=1显然是它的一个解。对应x=1可得此问题的解为（14，1，19）。

[6] 唐内里对原文中求这两平方数的段落加注了括号，其过程不同于卷Ⅲ，10题，并指出是没有必要给出的。10=10·1，

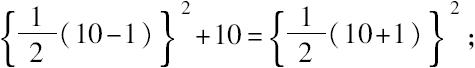
因此 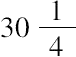是一平方数且比另一平方数大10。

类似地 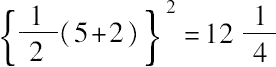也是如此的平方数。

但原文是，令m ² -10=（m-2） ² ，从而m= 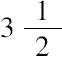，求出m ² =

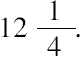
[7] Wertheim给出了如下更一般的解法。

如果取所求数为 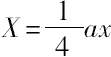，Y=ax+b ² 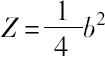， ，则两个条件已经满足，

亦即XY+Z ² =平方数，YZ+X ² =平方数。

仅剩一个条件ZX+Y ² =平方数还要成立。

即 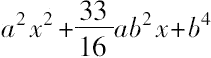=平方数。

令 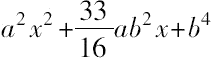=（ax+kb ² ） ² ，

则 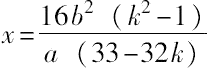，其中k可任意取值。

[8] 当然，用现代符号，此题可给出如下更漂亮的解法。（此注释也适合下题，卷Ⅲ，16题。）

若所求数为x，y，z，则xy+x+y，等等必须是平方数。

从而可得如下式子：

（y+1）（z+1）=平方数+1，

（z+1）（x+1）=平方数+1，

（x+1）（y+1）=平方数+1。

设平方数依次为a ² ，b ² ，c ² ，并令ξ=x+1，η=y+1，ζ=z+1，则有

ηζ=a ² +1，

ζξ=b ² +1，

ξη=c ² +1.

［这个问题实际上和卷Ⅴ，8题的引理相同。］

用第二个乘以第三个方程，并除以第一个，得

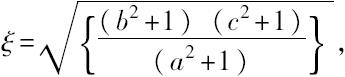
而η，ζ的表达式类似可得。

x，y，z是这些表达式依次减去1。

另外a ² ，b ² ，c ² 的选取应满足ξ，η，ζ的有理性。参见Euler，Commentatious arithmeticae，Ⅱ.

[9] 事实上，a ² （a+1） ² +a ² +（a+1） ² ={a（a+1）+1} ² .

[10] 此替换解无疑是丢番图的。丢番图已经解出了方程组

yz+y+z=u ²

zx+z+x=v ²

xy+x+y=w ²

费马后来用4个数替代3个数，想展示相应问题的解法。

为此他使用了丢番图卷Ⅴ，5题的解，亦即求x ² ，y ² ，z ² ，满足

y ² z ² +x ² =r ² ，z ² x ² +y ² =s ² ，x ² y ² +z ² =t ² ，

y ² z ² +y ² +z ² =u ² ，z ² x ² +z ² +x ² =v ² ，x ² y ² +x ² +y ² =w ² ，

丢番图的解答是

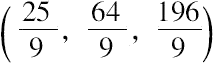
费马直接用来作为4个数的前3个，它们满足条件：其中任意两个之积加上该两数之和均为平方数，并令x为第4个数。6个关系式中有了3个已满足，另外3个要求

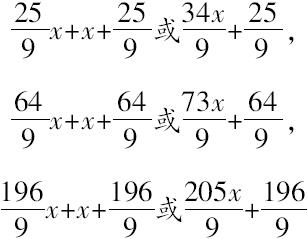
均为平方数：因此费马的方法实际上要解一个“叁重方程”问题。

但是费马没有给出具体答案。我怀着好奇想查证即便针对这相对简单的情况，“叁重方程”方法会导致多么复杂的数字。

为此，当然可以忽略公分母9，解方程

34x+25=u ² ，

73x+64=v ² ，

205x+196=w ²

由“叁重方程”得

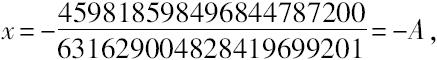
其中分母等于（251322303399） ² 。

为了查证此解是否正确，我们发现确实：

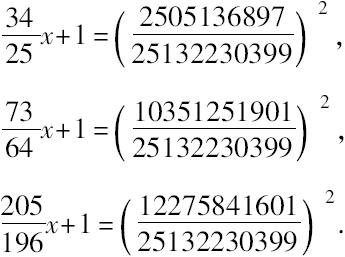
严格地说，由于所求x的值为负，在三个方程中，应该用y-A替代之，并重新开始，由此而引起大量计算，我只好放弃了。

[11] 此题可以和如下问题作比较，参见paragraph 42 of Part I.of the Inventum Novum of Jacobus de Billy（Oeuvres de Fermat，Ⅲ.）

求ξ，η（ξ＞η），使

ξ-ξη，

η-ξη，

ξ+η-ξη，

ξ-η-ξη

都是平方数。

假设η=x，ξ=1-x；则前两个条件成立。

由后两个条件得

x ² -x+1=u ² ，

x ² -3x+1=v ² .

把差2x分解成两个因子2x，1，

按常用方法，令 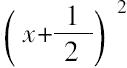=x ² -x+1，

从而 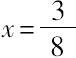，且所求数是

为了用上面的方法求出x的其他值，在双方程中，用 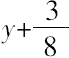代替x，从而

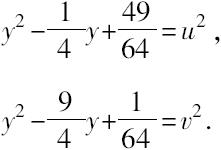
给第二个表达式乘以49，则有

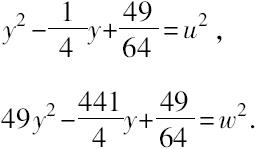
其差是48y ² -110y。

De Billy要求把这个差分解成两因子，当令两因子的差的一半的平方= 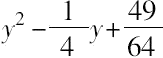时，方程两边常数项可以消失，为此，取两因子为 ，

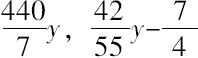如果令

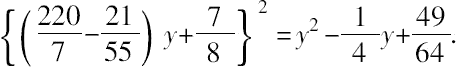
容易得出 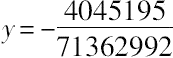，从而 ，

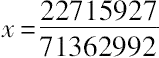所求数是

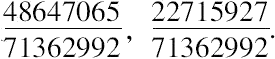
De Billy还提到如下另一个解，

把48y ² -110y分成两因子6y，

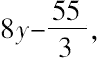
使其满足在所得的方程中x ² 项可以消失。

令 = ，

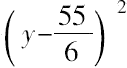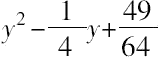从而 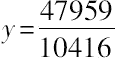，且

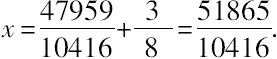
这会导致1-x的值为负。

但是，De Billy考虑到最初的双方程中x的对称性，因为 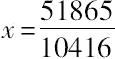满足它，

必然 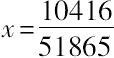也满足它。

从而所求数是

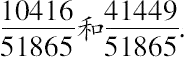
[12] 如果有两个数p，q，由其构造直角三角形就是选取数（p ² +q ² ，p ² -q ² ，2pq），作为直角三角形的边，因为（p ² +q ² ） ² =（p ² -q ² ） ² +（2pq） ² 。 CsIWsjF89ZyuP2JG91zSJiGSny5CCMrVylZddvk8GqJeswr1hXhBLrogjyS3J/L5