3-5 将极限概念应用于斜率

3-5-1 认识极小变量符号

在微积分中我们常使用Δ符号，这个符号念 delta ，符号 Δ x 代表 x 轴的 极小变量 。

3-5-2 用极小变量代表斜率

假设曲线函数如下：

y = f （ x ）

曲线上有一个 A 点，此点坐标是 （ x , f （ x ）） 。将 A 点微幅移动 Δ x 可以得到 B 点，这时可以得到 B 点坐标是 （ x +Δ x , f （ x +Δ x ）） 。那么我们可以得到直线 AB 的斜率公式如下：

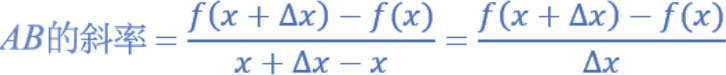
上述公式中，如果 Δ x 越趋近于0，代表 B 点越趋近于 A 点，上述公式就越趋近于曲线在 A 点的斜率。

3-5-3 应用极限概念在斜率上

在3-5-2节 AB 的斜率 公式中，不能直接设定 Δ x =0 ，因为这会使分母为0，同时这也不是 切线 的概念。

这时就可以应用极限的概念了，也就是 Δ x 趋近于0，这时可以推导得到下列 A 点的斜率。

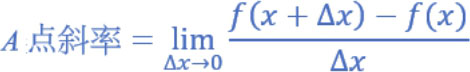
下面是图形概念表达。 hjEB7k9xVx/MXQASQ1JyKN1R8hJQTlZqi93yFz+k2Prtoh8wlw4Rq+0gYhYq3NNs