3-3 曲线上某点处切线的斜率

3-3-1 基本概念

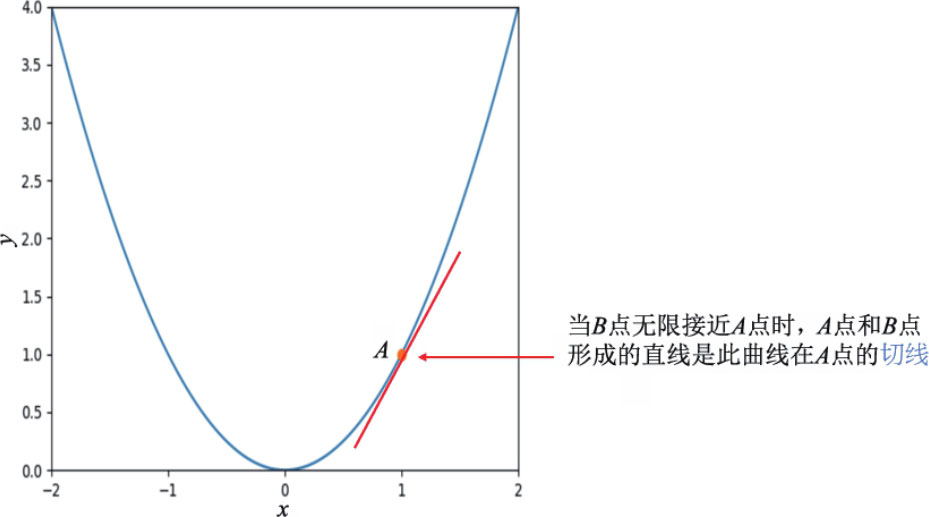
直线的 斜率 是 固定的 ，但是 曲线 上某点处切线的斜率会因所在位置不同而不同。

3-3-2 从曲线上2点连线的斜率说起

我们可以使用二次函数代表曲线。

程序实例ch3_1.py： 绘制一条 x 从 -5 至 5 区间的下列二次函数：

y = x ²

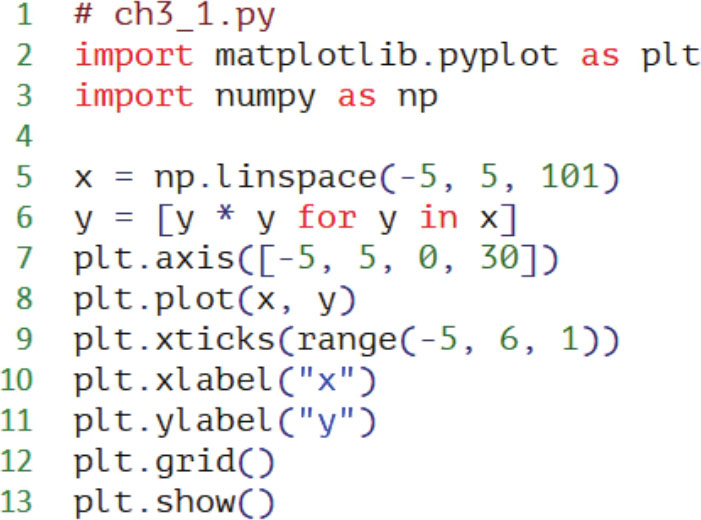
执行结果

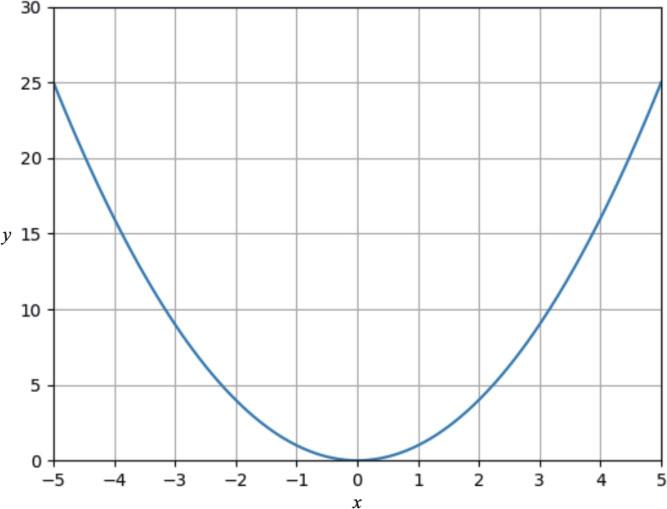
执行结果

假设现在想计算曲线 y = x ² 上的 A 点 和 B 点 形成的直线 AB 的斜率，使用我们已经知道的概念，可以使用下图表达。

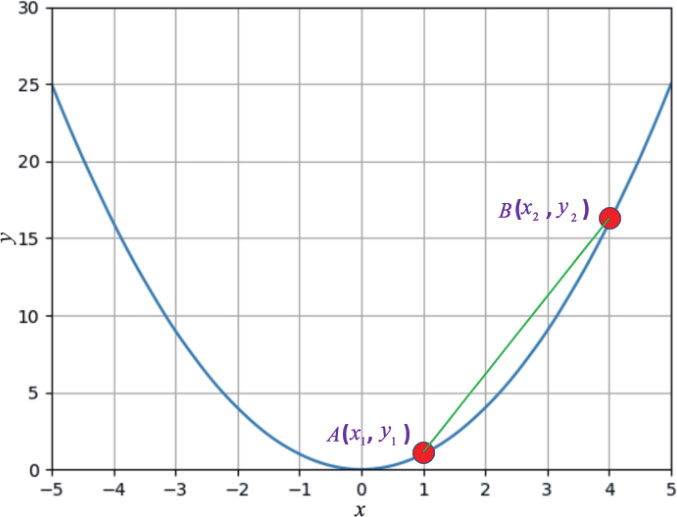
此时 A 点 坐标虽然是 （ 1, 1），但是我们先用（ x ₁ , y ₁ ）表达。 B 点 坐标虽然是（4, 16），但是我们先用（ x ₂ , y ₂ ）表达，此时的直线 AB 的斜率公式如下：

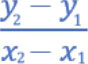
因为该曲线公式是 y = x ² ，所以 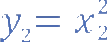， ，我们可以将上述公式改写如下：

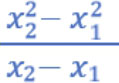
上述公式的计算结果如下：

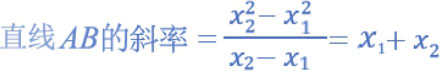
读者可能奇怪上述公式如何计算，我们可以使用下列方式 验算 ：

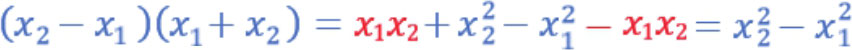
由上述公式验算，我们可以得到当曲线是 y = x ² 时，直线 AB 的斜率相当于是 （ x ₁ + x ₂ ） 。

由上图知， A 点坐标（ x ₁ , y ₁ ）其实是（1, 1）， B 点坐标 （ x ₂ , y ₂ ） 其实是（4, 16），由上述公式我们可以得到直线 AB 的斜率是：

x ₁ + x ₂ =1+4=5

3-3-3 曲线上某点处切线的斜率

现在将 B 点移近 A 点，移至（2, 4）的位置。

程序实例ch3_2.py： 重新设计ch3_1.py，但是更改 B 点的位置为（2, 4），同时连接 A 点和 B 点。

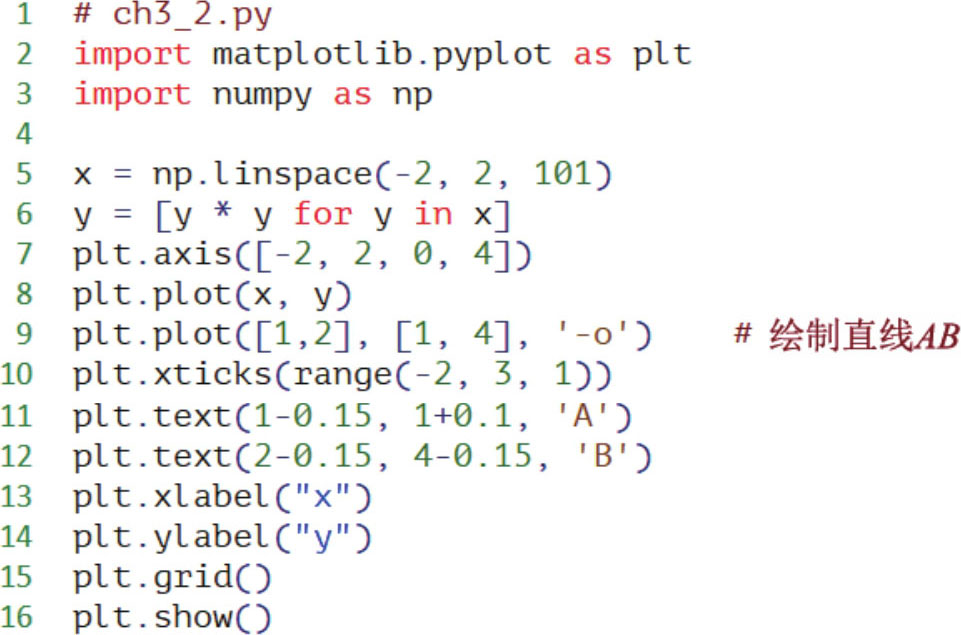
执行结果 这是笔者手动调整 x 轴和 y 轴相同单位长度的结果。

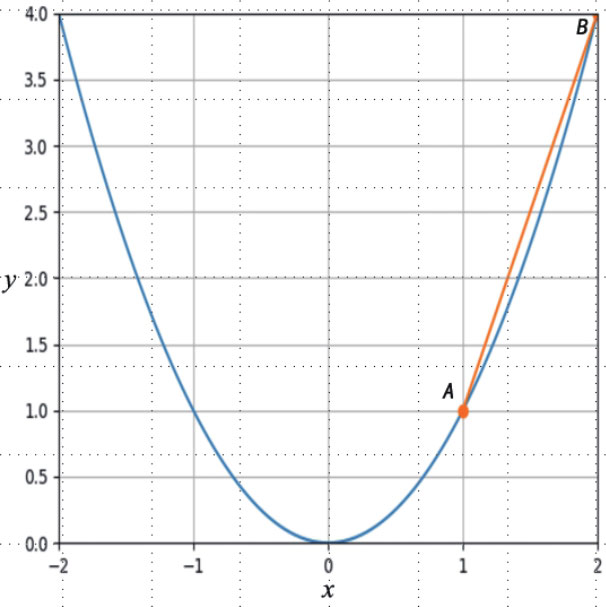
这时直线 AB 的斜率变成 x ₁ + x ₂ =1+2=3。从上述直线 AB 看，虽然此直线非常接近曲线 y = x ² ，但是上述计算方式不能称作曲线上 A 点处切线的 斜率 ，使用相同方法看弯曲程度较大的曲线：

很明显，上述曲线上的任意2点形成的直线的斜率均无法当作此曲线上 A 点处切线的斜率，如果要计算曲线上 A 点处切线的斜率，必须将 B 点移向 A 点，如下所示：

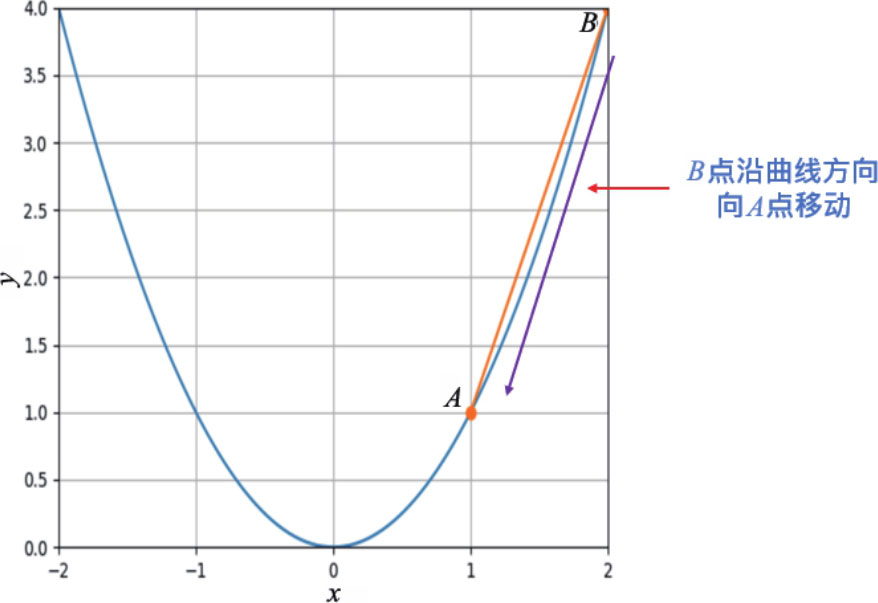
当曲线上的 B 点 趋近 A 点时， B 点坐标就非常靠近（ 1,1 ），则由 A 点和 B 点形成的直线 AB 的斜率就接近 x ₁ + x ₂ =1+1=2 ，当 B 点 无限接近 A 点时，由 A 点和 B 点形成的直线的斜率才是曲线上 A 点处切线的斜率，我们也可以将直线 AB 称为曲线在 A 点的 切线 。 NlKLv+mfRCTbnq230WsFevxw11IbrG+TDfh8hVx6Vgoc4c9HvLUCDq5aHu/H5cn4