当函数的 自变量 取 极限趋近某一个数值 后的结果是什么?这就是本节要讲述的 收敛 ( Convergence )与 发散 ( Divergence )。
注:极限趋近某一个数值 ,此 数值 不一定是无穷大,可以是0、1或其他值。
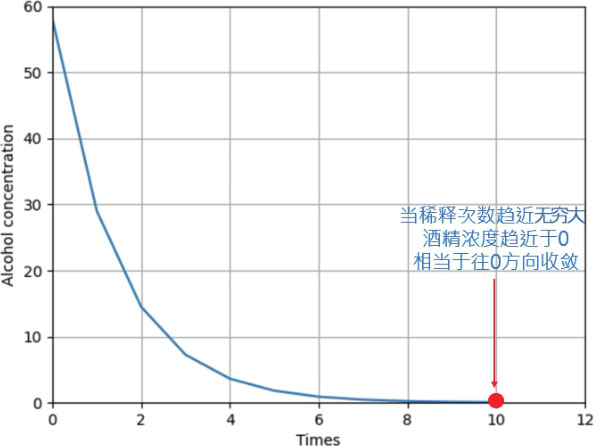
当函数的 自变量 取 极限趋近于一个值 ,若函数最后所得到的结果趋近于一个值,我们称此为 收敛(Convergence) 。请参考 2-1 节的金门高粱酒的稀释实例,当 稀释次数 趋近 无穷大∞ 时,可以得到此函数的结果是趋近于0,这时我们称此函数结果是 收敛 。
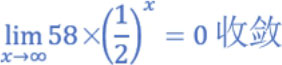
下图说明,当酒精稀释次数趋近于 无穷大∞ 时,结果趋近于0。
当函数的 自变量 取 极限趋近于一个值 ,若函数最后所得到的结果 无法趋近 于一个值,而是函数的结果变得更大或更小,我们称此为 发散(Divergence) 。例如:
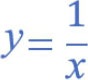
上述公式如果 x 值 从正值 右边趋近于 0时, y 值将持续变大,最后 y 值将趋向 极限值 ∞,这种结果我们称为 发散 。可以使用下列公式表达:
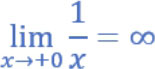
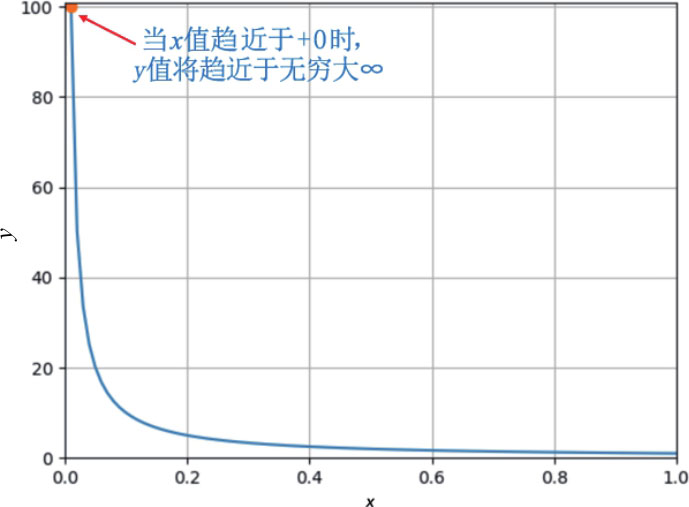
上述 x →+0表示是从右边趋近于0,最后发散至∞。
程序实例ch2_4.py: 用此节实例设计 x 值从1.0至0.01的结果。
执行结果
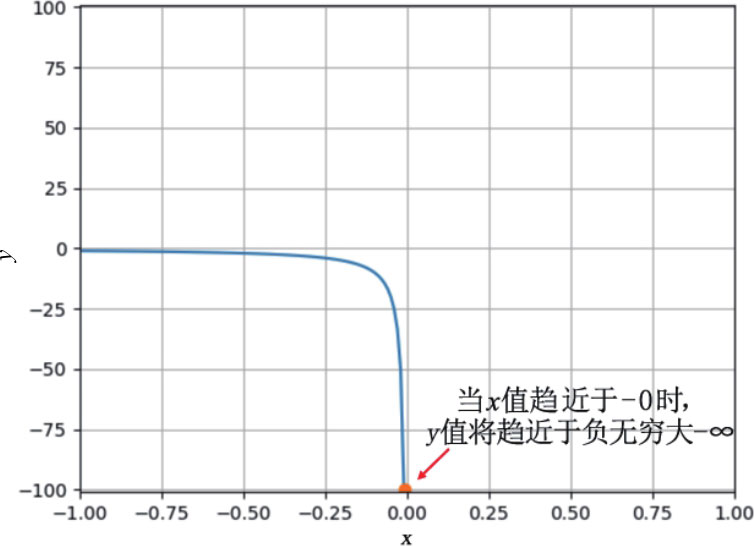
上述相同公式,但是让 x 值从 负值 向- 0 趋近,则整个公式表达如下:
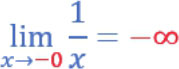
上述 x →-0表示是从左边趋近于 0 ,最后发散至-∞。
程序实例ch2_5.py: 使用相同程序,但是让 x 值 从 - 1 向 - 0.01 趋近,使用图表解释,同时列出结果。为了与前一个程序有区别,笔者特别绘制坐标轴的 x 轴是从 -1到1 , y 轴是从 -101到101 。
执行结果