2-1 从金门高粱酒说起

2-1-1 稀释金门高粱酒的酒精浓度

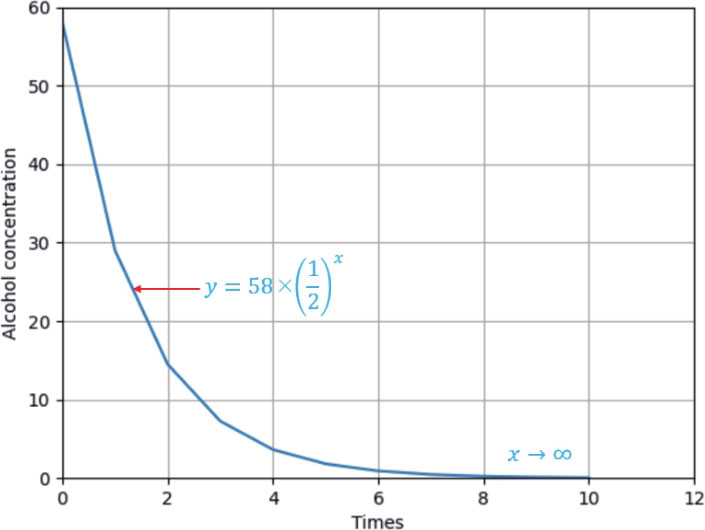
金门高粱酒的酒精浓度是 58% ，如果倒掉半瓶然后加入等量的水，这时金门高粱酒的酒精浓度变成 29% ，如果一直重复此步骤，高粱酒的酒精浓度会持续降低，如下所示：

58%, 29%, 14.5%, …

假设金门高粱酒酒精浓度的变量是 y （单位： % ），则最开始 y =58 ，假设稀释酒精次数是 x ，则可以使用下列函数代表此高粱酒的 酒精稀释 的过程与结果：

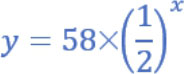
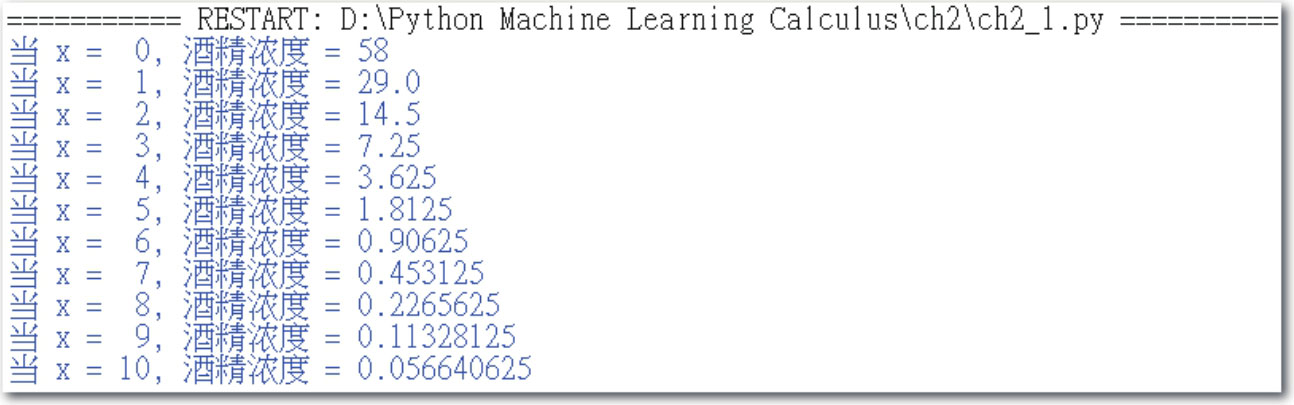
程序实例ch2_1.py： 在上述高粱酒的酒精稀释的过程中，计算当酒精稀释次数 x 从0至10的酒精浓度的变化过程。

执行结果

程序实例ch2_2.py： 重新设计ch2_1.py，使用图表方式表达。

执行结果

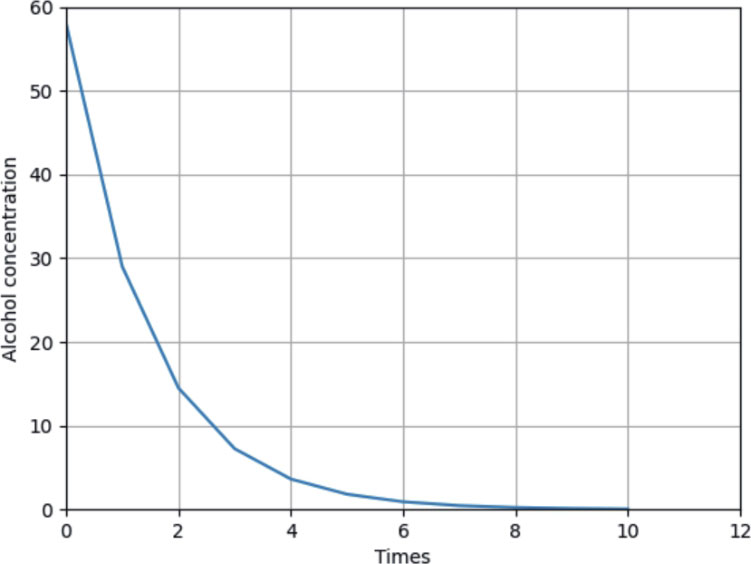
从前面2个程序实例可以看到，当 x 值 （稀释金门高粱酒的酒精浓度的次数）越来越大时，甚至趋近于无限大时， y 值 （酒精的浓度）将越来越小， y =0.00…001 ，最后趋近于0。

2-1-2 极限值的数学表示方式

在数学表达式中， 无穷大 表示方式如下：

∞

如果还要细分，可以称上式是 正无穷大 ， 负无穷大 的表示方式如下：

-∞

不过，通常 无穷大 若不特别指明，就是指 正无穷大 ∞。

2-1-3 变量趋近极限值

极限的符号是lim，如果要表达 变量 x 趋近于 无穷大∞ 时，可以使用下列公式表达：

2-1-4 调整金门高粱酒酒精浓度的表达方式

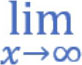
依据上述小节的概念，可以使用下列方式表达金门高粱酒的稀释公式：

2-1-5 完整表达公式

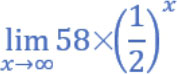
从前面程序实例可以看到，当 x 值 （稀释金门高粱酒的酒精浓度的次数）越来越大时， y 值 （酒精的浓度）将越来越小， y =0.00…001 。如果我们想要表达当 x 趋近于 无穷大∞ 时，酒精浓度将趋近于 0 ，可以使用下列方式表达：

2-1-6 概念总结

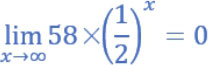
理论上，不论如何稀释酒精浓度，酒精含量一定存在。如果连续不中断地稀释此金门高粱酒，我们可以将酒精浓度视为 0 。我们可以使用下图更完整地表达此概念。 XDyyVJxYFZTSpRGjmdrpk6ky30KLEwG6SBU4qwRQ3vx8IRi51KLGkIjHWN+mNURx