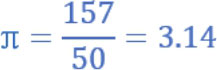下载掌阅APP，畅读海量书库
立即打开
学术发展的起源是因为在不同阶段有不同需要，事实上在微积分的历史中，是先有积分，后有微分。
在古代数学的发展中，从工作需求出发，逐步推导，最后有了积分学。
3000多年前的古埃及，雨水虽然孕育了沙漠的绿洲，但雨下得太大也会让尼罗河泛滥成灾，往往造成土地样貌的改变，此时需要对土地重新测量与规划，为了测量尼罗河河道改变产生的弯弯曲曲的土地，人们发明了类似积分的概念。
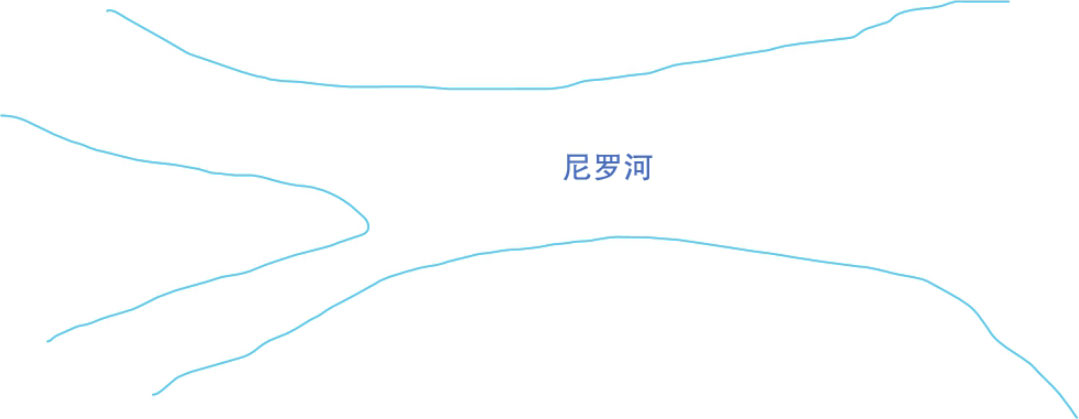
为了测量河道边土地的面积，人们使用绳子测量长度，先测量刚好大小的长方形，再测量较小的区块，整个概念如下图所示。
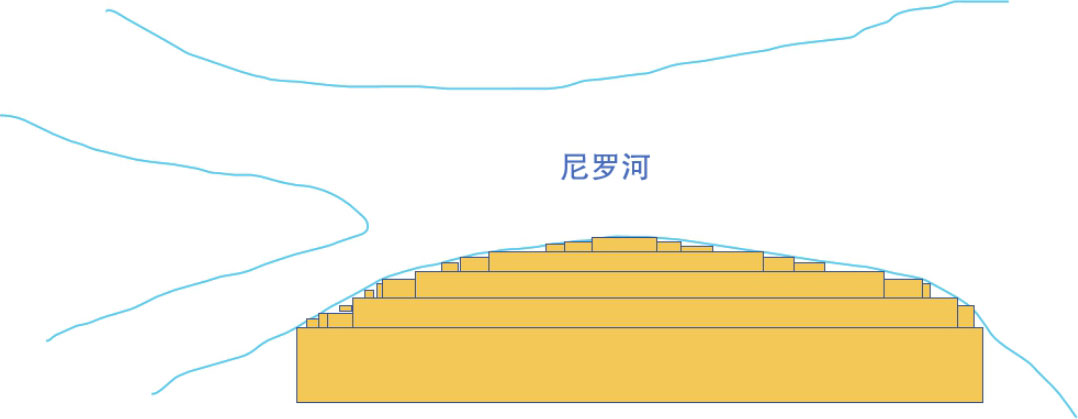
上述方法在数学上称为 穷尽法 （Method of Exhaustion），其实这个方法就是用无穷无尽的逼近去计算结果，如果经过数学推导，这个方法就会和 积分 产生关联。
1．欧多克索斯
古希腊的数学家、医学家、天文学家 欧多克索斯 （公元前408—前355年）曾使用 穷尽法 来计算 面积 与 体积 。
2．阿基米德
古希腊的数学家、物理学家、天文学家阿基米德（公元前287—前212年）利用穷尽法计算球的表面积、球的体积和椭圆面积，后代数学家依据他的概念发展成近代的微积分。
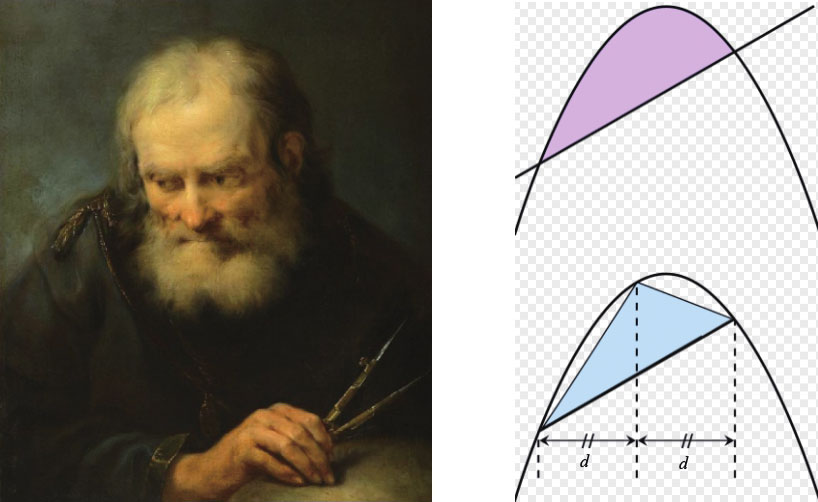
此外，他还证明了下述公式：
美国数学史学家E. T.贝尔在其所著的 Men of Mathematics 一书中，将 阿基米德 、 牛顿 和 高斯 并列为有史以来最伟大的三位数学家。
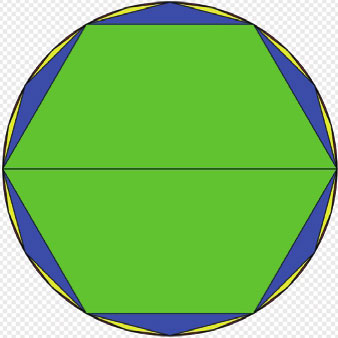
三国时代魏国数学家刘徽也使用 穷尽法 计算圆面积，其概念是用切割圆的方法计算圆周率，可以参考右图。
从圆的内部正六边形开始，然后逐步加倍，最后计算到正192边形，得到圆周率的近似值：
古代埃及人建立了积分萌芽的基础后，两位古希腊的数学家 欧多克索斯 和 阿基米德 接棒将相关知识继续发展，不过有一段相当长的时间，微分与积分是分开应用的，彼此关联的概念并没有被发现，所以一直没有被一起讨论，直到17世纪两位欧洲的天才数学家 牛顿 和 莱布尼茨 将微分与积分概念澄清与整合，使其大量应用于 几何学 、 物理 与 科学 的研究中。
如今 人工智能 的发展，细分为 机器学习 与 深度学习 ，大量使用微积分概念，因此 微积分 已成为当今计算机领域的重要基础知识。
艾萨克 · 牛顿 （Isaac Newton，1643—1727）是英国的 物理学家 、 数学家 、 天文学家 ，毕业于剑桥大学。他发现了 万有引力 （Law of Universal Gravitation）、 运动定律 （Law of Motion），这是现代工程学的基础，同时也奠定了 物理学 、 天文学 的基础。牛顿躺在苹果树下，因为苹果掉落而发现万有引力，据说是虚构的。
牛顿的母亲曾经想让牛顿当农夫，所幸当时国王中学的校长 亨利斯 · 托克斯 发现了牛顿的潜力，说服了牛顿的母亲，牛顿得以回到学校继续完成他的学业，同时完成了一篇优秀的毕业报告，最后申请到了 剑桥大学 ，开始迈向科学巨人之路。
在求学期间，牛顿对于 笛卡儿 的 几何学 著作进行了非常认真的研究，特别对于曲线的切线求法十分感兴趣，同时思索是否有更好的解决方法，牛顿在25岁左右开始有了 微积分 的框架。1665年，他发明了广义二项式定理，同时发展了新的数学理论，这就是我们现在所探讨的微积分。在1666年他有了数学史上第一个有关微积分的论文 流数简论 ，这是物理学运动定理中有关 微分 、 积分 的概念，因为可以描述物体在拋物线下的运动过程，因此开始受到了关注，只是牛顿没有正式发表，只在朋友间流传。牛顿的第一本正式著作是于1669年发表的 De analysi ，一般称这是第一本微积分著作，同样只在朋友间流传。这本著作直到1711年才出版。
注： 正流数术 就是指 微分 ， 反流数术 是指 积分 。
牛顿在1671年完成了第2本著作《流数法与无穷级数》（ Method of Fluxions and Inf i nite Series ），这本书直到1736年才出版。
牛顿在1676年发表了《曲线求积法》（ Tractatus de Quadratura Curvarum ），这本著作直到 1704 年才出版。
牛顿在1687年正式出版了 Principia ，这本书的算法就是所谓的 微积分 ，不过所使用的符号却采用了古典几何学的方法，使用上不太方便，同时使人难以理解。
下面是 牛顿 所使用的 微分 与 积分 符号。
由于此著作出版时间是 1687 年，相较于欧洲科学家 莱布尼茨 晚了 3 年，这也使究竟谁是发明微积分的人成为数学界最大的争议。
其实牛顿在 光学 与 力学 领域皆很有成就，但这些不属于本书叙述范围。
莱布尼茨 （Leibniz，1646—1716）是德国的 数学家 、 哲学家 ，也是一位 律师 ，是历史上少见的全才，他的许多数学公式皆是往返各大城市间在颠簸的马车上完成的。
莱布尼茨与牛顿几乎是同一时期的代表性人物，莱布尼茨于1684年在 Acta Eruditorum 杂志发表了有关 微分的 论文《极大与极小值的新方法》（ Nova Methodus pro Maximis et Minimis ）。在这篇论文中，莱布尼茨使用了 d x 和 d y 的 微分 符号。
1686年，莱布尼茨在 Acta Eruditorum 杂志上发表了有关 积分 的论文《深度隐藏的几何学和无限小与无限大的分析》（ De geometria recondite et analysi indivisibilium atque in fi nitorum ），在这篇文章中他使用了 积分 符号 ∫ ，这个积分符号类似 S um（总和）的首字母 S ，然后将它拉长，称为 Integer ，具有 总和 或 加总 的意义。
莱布尼茨 在发明微积分时意识到好的数学符号可以利于思考，增加学习效果，所以他创设的微积分符号远优于牛顿所创的符号，我们现在所用的微积分符号就是当时 莱布尼茨 所创。
1714—1716年， 莱布尼茨 在过世前完成了《微积分的历史和起源》，这篇文章直到 1846 年才发表，在这篇文章中，莱布尼茨叙述了他独立完成微积分的起源与思维。
现在数学家一般认为 牛顿 与 莱布尼茨 分别独立发明了微积分，不过 莱布尼茨 的数学符号在使用上较为方便，因此成为我们学习 微积分 的主流。