




石墨烯是一层蜂窝状排列的碳原子晶格结构。这种材料的光学特性可以追溯到它的导电性,主要受电子的带内和带间跃迁所控制。如图2.13所示,一种为价带和导带之间的跃迁,另一种为导带内的电子跃迁,而不同的跃迁行为通常伴随不同的光效应。两种跃迁共同贡献石墨烯的电导率 [100] ,即
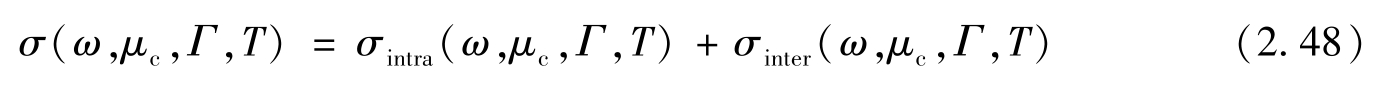
式中: ω 为工作角频率; Г 为载流子散射率; T 为温度; μ c 为化学势。当石墨烯生长和转移到衬底(散射率被确定),且工作环境(指应用背景如工作频率、环境温度)确定后,可以动态改变的变量就是对应的费米能级。而后者主要取决于石墨烯本身载流子浓度的高低,可以通过电压、电场、磁场或化学掺杂等控制。
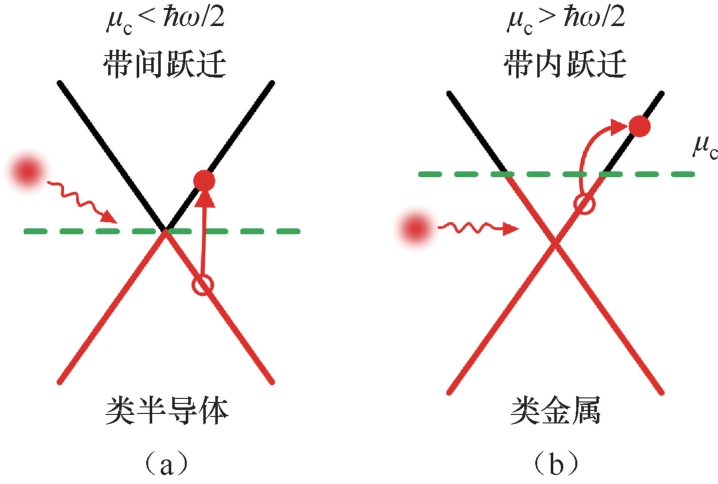
图2.13 石墨烯电子带内与带间跃迁的能带示意图 [2]
在没有外部磁场存在时(如不存在霍尔电导),石墨烯上的电导率 σ 可以认为是均匀各向同性的。可根据Kubo公式 [101,102] 表示为
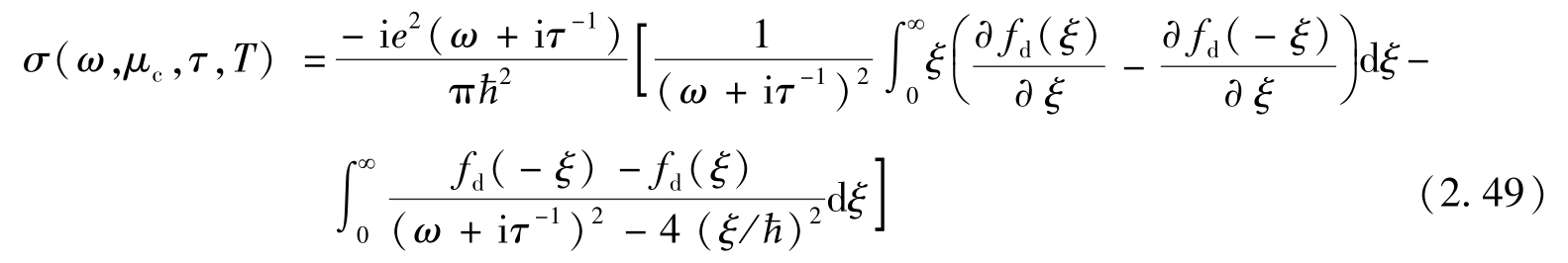
式中:
ω
为角频率;
τ
为载流子弛豫时间(
Γ
可以与
τ
=(2
Γ
)
-1
互换);
e
为电子电量;
ħ
=
h/
(2π)为约化普朗克常数;
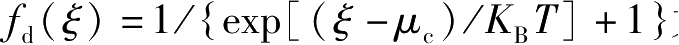 为费米—狄拉克分布函数(
K
B
为玻尔兹曼常量)。式(2.49)右项分别包含带内跃迁
σ
intra
和带间载流子跃迁
xσ
inter
的贡献和。
为费米—狄拉克分布函数(
K
B
为玻尔兹曼常量)。式(2.49)右项分别包含带内跃迁
σ
intra
和带间载流子跃迁
xσ
inter
的贡献和。
当石墨烯的工作温度为室温300K时, K B T ≈0.026eV,远远小于工作电压偏置下的石墨烯化学势 μ c ,即 K B T <<| μ c |。则石墨烯电导率的带内跃迁 σ intra 和带间跃迁 σ inter 可以分别简化为 [103,104]
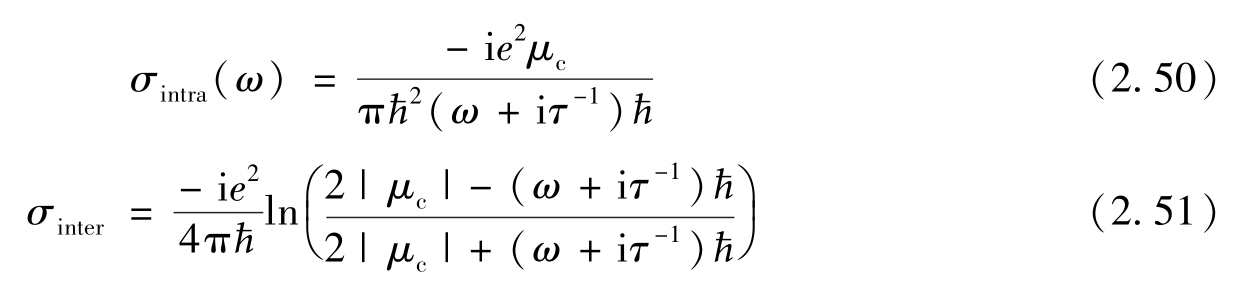
所以在任意偏置电压下(此处假设石墨烯化学势 μ c =0.4eV),对应的带内跃迁 σ intra 和带间跃迁 σ inter 所带来的电导率变化曲线如图2.14所示。从图2.14中可以看出石墨烯的电导率具有以下几个特点。
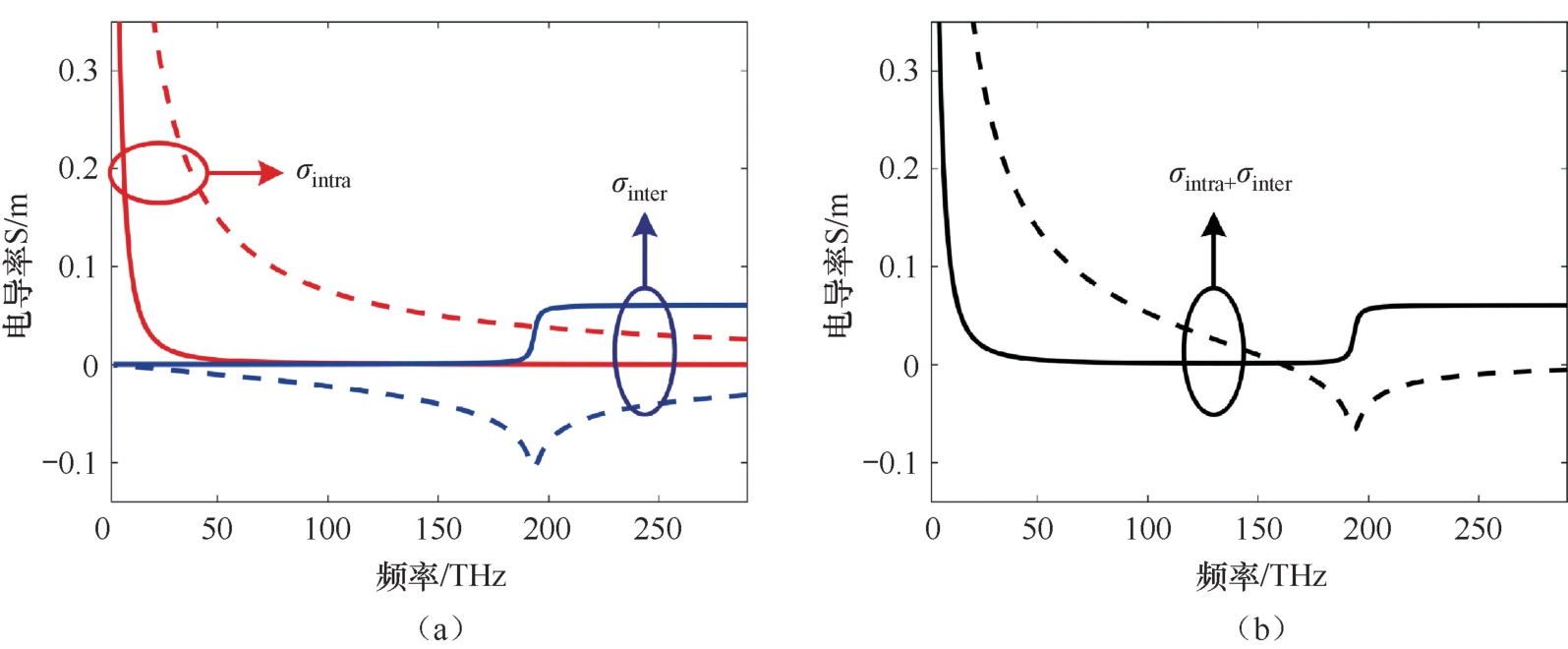
图2.14 不同工作频率下(从THz到可见光频段),石墨烯电导率的变化趋势,对应的石墨烯的化学势为0.4eV。(a)石墨烯的带内跃迁及带间跃迁对应的实部与虚部随工作频率改变的变化曲线;(b)总的电导率变化趋势
(1)带内跃迁带来的电导率实部及虚部均随频率降低而逐渐增强,且虚部大于实部,而带间跃迁则相反。表现的行为是低频时带内跃迁占主导,高频时带间跃迁更易发生,这也可从图2.14(b)的电导率曲线直观地看出。
(2)在频率比较低的时候(远红外光及以下), μ c >1 / 2 ħω ,泡利阻塞发生,也即入射光子的能量不足以激发价带电子向导带的跃迁时,石墨烯的电导率主要由 σ intra 占主导地位。此外, σ intra 的实部和虚部均为正数且虚部比实部大时,石墨烯是一种具有损耗特性的感性材料,且损耗特性比电感特性更加明显。其色散曲线类似金属的Drude模型 [105,106] 。
(3)随着频率的逐步升高(红外光), σ intra 实部迅速减小,而虚部依然比较大。另外, σ inter 实部依旧近乎0,但是虚部也在减小(负数),在这个频段附近出现了一种很奇特的现象,也就是将带内贡献和带间贡献相加,石墨烯总的电导率实部很小,而虚部相对较大(正数),此时的石墨烯在红外光附近对TM模式的表面波支持较好。这部分内容将在后面章节结合案例详细阐述。
(4)当频率进一步升高,满足
μ
c
<1
/
2
ħω
时,
σ
inter
会有一个跃变,这种跃变现象是由于当入射电磁波交换的能量大于价带、导带两端化学势之和(-
μ
c
~
μ
c
,石墨烯是一种零隙半导体,没有禁带),价带中的电子可以占据更高的量子态;跃变后,实部从近乎0上升到一个常数,这个常数也就是石墨烯的最小表面电导率,即
σ
min
=Re(
σ
inter
)=
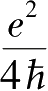 =6.085 e
-
5
S,与实验观测到的数值近乎一致
[107,108]
。
=6.085 e
-
5
S,与实验观测到的数值近乎一致
[107,108]
。
在波长相对较长的低频(微波或太赫兹频段),波长与石墨烯厚度的巨大差异将使三维模型的石墨烯的仿真变得困难。此时零厚度的二维简化模型比较适合。石墨烯的表面阻抗可以表示为 [109]
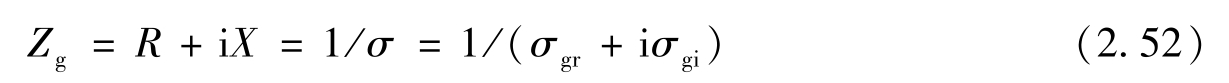
式中: R 为表面阻抗实部,对应石墨烯的吸收损耗; X 为表面阻抗虚部,对应石墨烯呈容性还是呈感性。显然 R 和 X 的绝对大小由电导实部( σ gr )和虚部( σ gi )共同决定,而石墨烯呈容性还是呈感性,则取决于表面电导率实部 σ gr 。
石墨烯的等效介电常数模型可由麦克斯韦方程组推导,适用性比较广,便于理解石墨烯的电磁属性,并且可以解释石墨烯在不同频率下呈现奇特的电磁现象。
考虑外加电场 E 的作用,可以得到石墨烯的传导电流 J=σ v E=σ/t E ,其中 σ v =σ/t 表示石墨烯的体电导率, t 为石墨烯厚度,而其物理厚度为一个碳原子直径大小,远远小于其工作波长,给数值仿真带来了很大挑战,所以往往在不影响宏观电磁现象精确度的前提下,可取其等效的厚度。将传导电流 J 代入麦克斯韦方程:∇ ×H = J -i ωε 0 E=- i ωε g E 便可以提取石墨烯等效介电常数

进一步求得 ε g 的实部和虚部
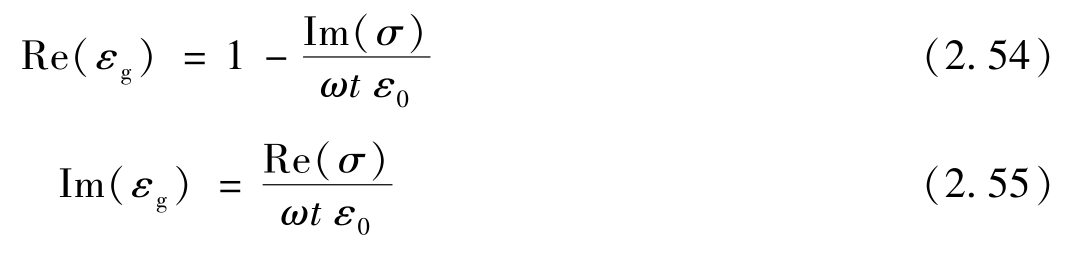
所以石墨烯的等效介电常数实部受电导率虚部影响,而虚部则受电导率实部影响。需要强调的是,当石墨烯建模成一层有厚度(定义石墨烯厚度为 t )的薄层材料时,不能简单地将其定义为各向同性介质。假设石墨烯垂直方向为 z 轴,则其相对介电常数可以用对角张量来表示

式中:
ε
xx
和
ε
yy
均为面内介电常数,可用式(2.53)计算,即
ε
xx
=ε
yy
=ε
∞
+
i
σ/
(
ωε
0
t
);
ε
zz
为法向分量,可用石墨的介电常数表示,即
ε
zz
=2.5。材料的折射率与其自身的介电常数满足
n=
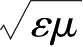 。石墨烯磁导率
μ
=1,则其折射率可表示为
n
=
。石墨烯磁导率
μ
=1,则其折射率可表示为
n
=
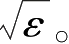 因此,石墨烯光学参数最终可由其电学参数确定。由前节推导可知,在工作温度、波长及散射率确定之后,石墨稀的相对介电常数实部对应电导率的虚部,且只和化学势有关,或者可以说,改变石墨烯的化学势就可以对石墨稀的折射率进行调节。
因此,石墨烯光学参数最终可由其电学参数确定。由前节推导可知,在工作温度、波长及散射率确定之后,石墨稀的相对介电常数实部对应电导率的虚部,且只和化学势有关,或者可以说,改变石墨烯的化学势就可以对石墨稀的折射率进行调节。
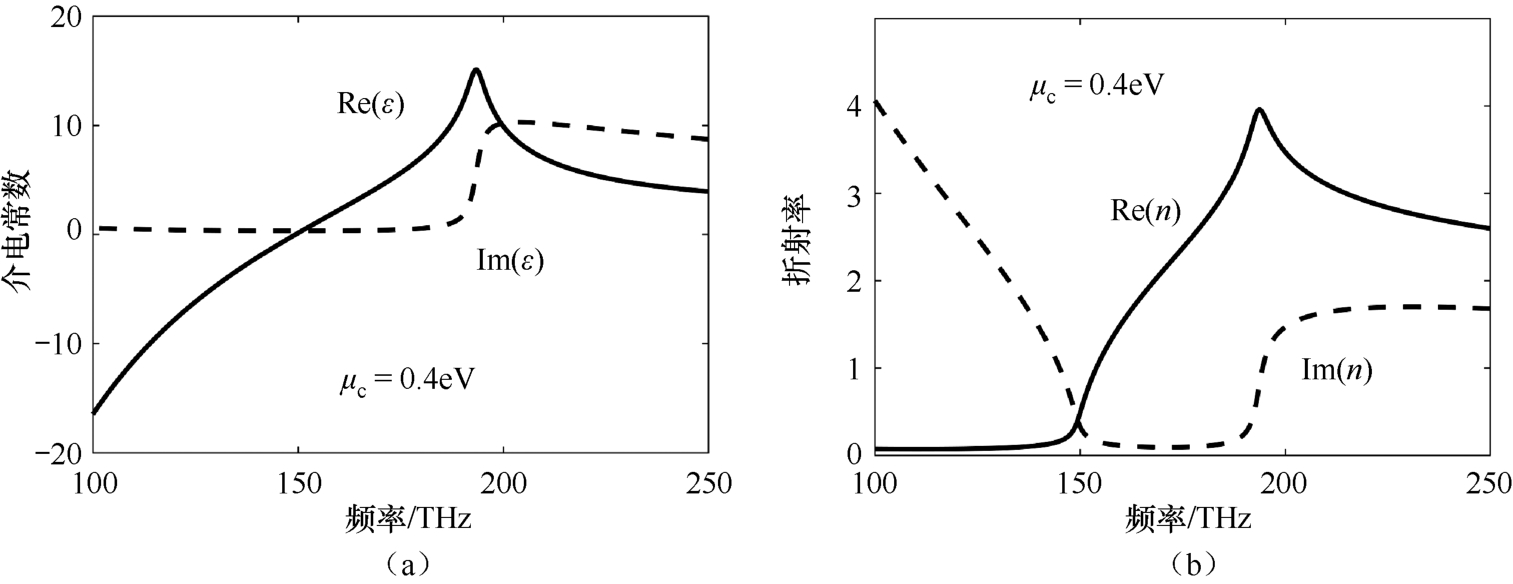
图2.15 不同工作频率下(从THz到可见光频段),石墨烯介电常数及等效折射率的变化趋势,对应石墨烯的化学势为0.4eV。(a)石墨烯的介电常数的实部与虚部随工作频率改变的变化曲线;(b)石墨烯的折射率的实部与虚部随工作频率改变的变化曲线
图2.15及图2.16分别给出了0.4eV的化学势下,石墨烯的介电常数及等效折射率随工作频率的变化,以及特定工作频率下(两个典型光通信波长 λ 0 =1.31μm、 λ 0 =1.55μm),两者随掺杂浓度(石墨烯化学势)的变化曲线。在给定石墨烯的化学势的前提下,如当 μ c =0.4eV时,如图2.15(a)所示,当工作频率从100THz的相对低频变到250THz的高频时,石墨烯介电常数实部先小于零(小于150THz),然后随着频率变高大于零;而虚部先从零,在经过 μ c =1 / 2 ħω 点时,突增到接近10的正值。这一变化过程中,石墨烯工作在低频时,呈现金属特性,而随频率升高渐渐向介质属性转变。而对应等效折射率则表现为,低频时(小于150THz),折射率实部小于1,呈现金属特性,此时的石墨烯支持表面等离激元;而150~193THz的频段,折射率实部变大,虚部接近零,此时的石墨烯表现为近乎透明的介质材料;而当工作频率大于193THz时,石墨烯虚部显著增加,此时的石墨烯表现为有损耗的介质层。
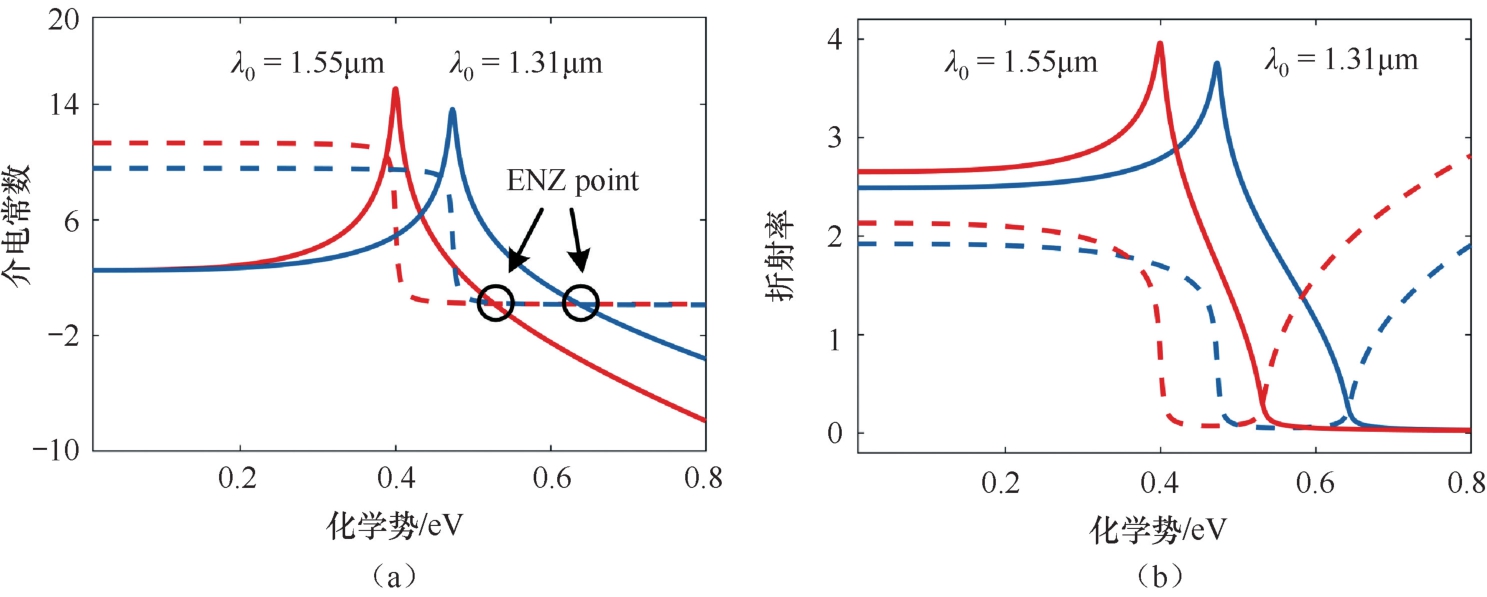
图2.16 不同石墨烯化学势(掺杂浓度)下(0~0.8eV),石墨烯介电常数及等效折射率的变化趋势。对应的波长分别为 λ 0 =1.31μm、 λ 0 =1.55μm。(a)石墨烯的介电常数的实部与虚部随石墨烯化学势改变的变化曲线;(b)石墨烯的折射率的实部与虚部随石墨烯化学势改变的变化曲线
在特定工作频率下,进一步观察石墨烯的介电常数及折射率随掺杂浓度(石墨烯化学势)的变化曲线。以典型的光通信波长 λ 0 =1.31μm, λ 0 =1.55μm为例,当工作环境确定后,石墨烯的介电常数的虚部及实部在开始时全为正数,石墨烯表现为一种有损耗的介质层,当掺杂浓度继续加大到接近 μ c =1 / 2 ħω 时,石墨烯介电常数实部依然大于零,而介电常数虚部则突变为零,此时的石墨烯泡利阻塞抑制吸收,呈现为透明的介质层,当掺杂浓度进一步提升时,石墨烯的介电常数慢慢小于零,对应的折射率实部也开始小于1,此时,石墨烯渐渐往金属转变。一个有趣的点便是,在经过0.52eV(1.55μm)和0.63eV(1.31μm)的点时,石墨烯的介电常数实部及虚部均接近零,此时产生了一个介电常数接近零的点(ENZ point),如图2.16(a)中两个小圆圈所示。当工作于两个通信频段时,石墨烯的介电常数及等效折射率表现出相同的变化趋势,仅特征频率点随频率升高发生了蓝移。