




石墨烯的电子态可由无限延伸于有限能量范围(能带)内具有本征能量空间的无数周期波函数来表示。通常用三维空间坐标 r =( x , y , z )来描述某一现象,但对于周期波函数,用波数描述的坐标(倒格子空间或 k 空间)上的傅里叶变换乘积来表示会更方便。因此,在能带内由波函数 Ψ k ( r )描述的每个电子态都可用波数 k (波长的倒数)或乘以2π来表示。这里沿 x , y , z 方向的波数 k x , k y , k z 由波数矢量(又称波矢) k 来描述,这称为晶体中电子的能带结构 [22,23] 。
图2.1(a)为位于空间坐标上的部分石墨烯蜂窝状晶格。虚线表示一个原始的蜂窝状晶格单元,包含两个单独的碳原子,分别标记为
A
和
B
。即石墨烯蜂窝状晶格是由
A
和
B
碳位点组成的两个三角形子晶格连接而成的,两个子晶格结构在数学拓扑上具有二分格点系统的特征。石墨烯的晶胞基矢可以写成:
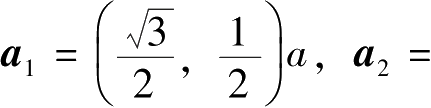
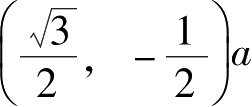 。其中,
。其中,
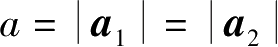 =2.46Å为晶格常数。则石墨烯蜂窝晶格中任意格点位置可以用晶格矢量
R
=
n
1
a
1
+
n
2
a
2
(
n
1
,
n
2
=0,±1,±2,±3,…)表示,其中最近的相邻碳位点(
A
和
B
位点)由矢量
τ
2
=
=2.46Å为晶格常数。则石墨烯蜂窝晶格中任意格点位置可以用晶格矢量
R
=
n
1
a
1
+
n
2
a
2
(
n
1
,
n
2
=0,±1,±2,±3,…)表示,其中最近的相邻碳位点(
A
和
B
位点)由矢量
τ
2
=
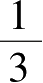 (
a
1
+
a
2
)连接。
(
a
1
+
a
2
)连接。
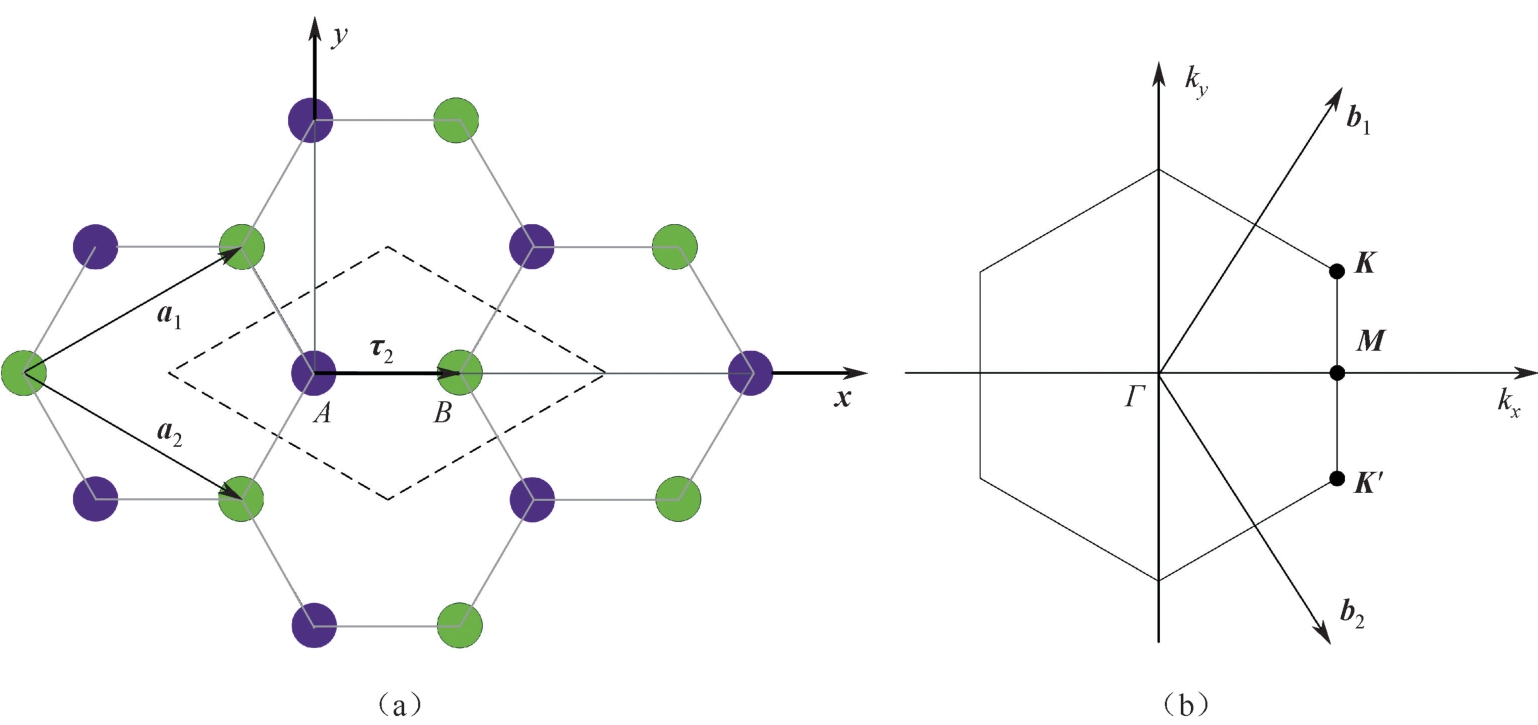
图2.1 (a)石墨烯的蜂窝状晶格;(b)蜂窝状晶格的倒格子 [23]
需要注意,基矢的选择并不是唯一的,如在带状石墨烯中,考虑边缘几何形状整体的对称性,可以选择不同的晶格基矢。在图2.1(b)中,晶胞基矢对应的倒格矢
b
1
=
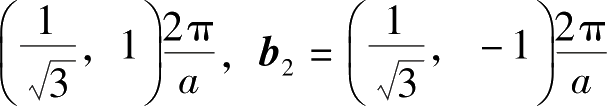 。倒格矢空间和实空间的对应关系满足:
b
1
·
a
1
=
b
2
·
a
2
=2π,
b
1
·
a
2
=
b
2
·
a
1
=0。
Γ
点是倒格子原点,实线六边形为倒格矢
b
1
、
b
2
表示的晶格的原胞。倒格子的原胞通常称为(第一)布里渊区,其中高度对称的点被标记为
K
=
。倒格矢空间和实空间的对应关系满足:
b
1
·
a
1
=
b
2
·
a
2
=2π,
b
1
·
a
2
=
b
2
·
a
1
=0。
Γ
点是倒格子原点,实线六边形为倒格矢
b
1
、
b
2
表示的晶格的原胞。倒格子的原胞通常称为(第一)布里渊区,其中高度对称的点被标记为
K
=
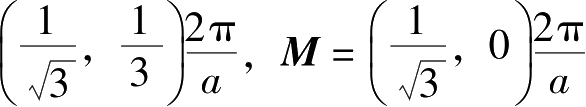 。由于石墨烯蜂窝状晶格的原胞中存在两个晶体学上独立的原子,所以
K
点可分为
K
和
K′
点两种类型。
K
和
K′
点附近的区域又称“谷”。
。由于石墨烯蜂窝状晶格的原胞中存在两个晶体学上独立的原子,所以
K
点可分为
K
和
K′
点两种类型。
K
和
K′
点附近的区域又称“谷”。
在石墨烯中,每个碳原子的2s轨道和两个2p轨道杂化,形成由3/4价电子填充的σ带;而比σ带具有更高能级的p z 轨道则构成了1/4价电子填充的π带。未参与杂化的p z 轨道与σ带的电子态正交。因此,石墨烯蜂窝晶格中相邻碳原子的p z 轨道的相互作用可以很好地描述具有最高能量(费米能量)的填充电子的电子态,并可通过紧束缚近似计算费米能量附近的能带结构 [24] 。在紧束缚模型中,只考虑相邻碳原子之间的相互作用。因此,相邻p z 轨道波函数之间的重叠可以忽略不计,石墨烯π带中一个电子的哈密顿量表示为
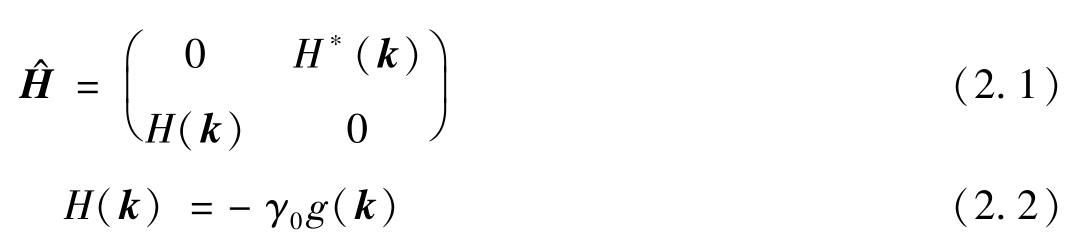
其中,共振积分 γ 0 和 g ( k )定义为
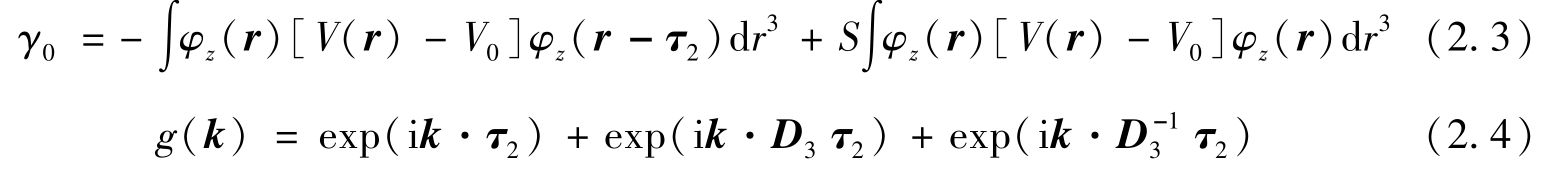
式中: r 、( φ z r )、 V ( r )、 V 0 、 D 3 分别为电子的位矢、碳原子的p z 轨道、石墨烯的晶格势、碳原子的原子势和120℃旋转算符。
γ 0 为最近邻碳原子之间电子相互作用的参数,约为3.15eV。为了对角线化 H ^,使薛定谔方程具有非零解,石墨烯π带的能量 E 可从以下特征方程得到:
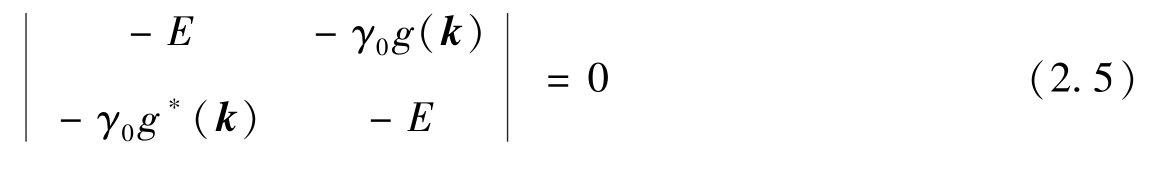
式中:波数矢量 k =( k x , k y ),代表石墨烯π带的电子态,与处于 p = ħk 状态的电子动量的特征值相关。最后,得到石墨烯π键的能量为
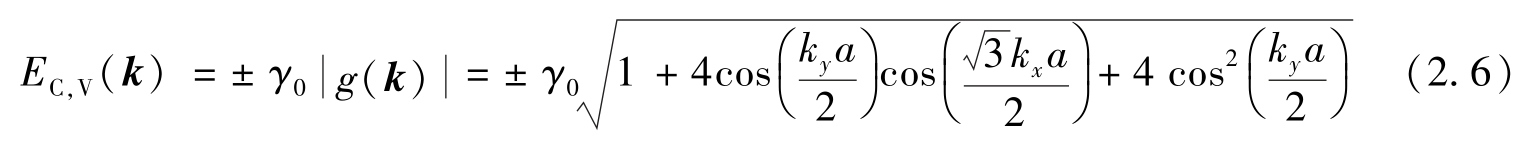
式(2.6)中的正负号分别对应 E C 和 E V ,其中C和V分别表示导带(π键)和价带(π * 键)。在这里,每个碳原子都有一个电子被容纳到产生的π键和π * 键中,其中π带被填满,π * 带没有被占据。因此,石墨烯中最高能量的填充电子也即费米能量,是位于π带和π * 带之间。此后,电子能量的原点固定在费米能量处。通常,电子能量 E ( k )作为晶体中波函数的波数矢量的函数称为“色散关系”。
由于晶体结构的平移对称性,石墨烯的任何电子态都可由倒格子空间( k 空间)中的波数矢量在布里渊区的波函数表示。图2.2(a)给出了由式(2.6)计算的 E C,V ( k )的三维曲线图,其中价带和导带相互接触的点(圆圈标记的点)称为狄拉克点 [25] 。沿图2.2(a)中布里渊区的 K 、 Γ 、 M 点的截面如图2.2(b)所示 [26] 。根据图2.2(b)所示的截面图,在图2.2(a)所示的三维曲线图中,狄拉克点位于 K 点 k x 和 k y 轴上,费米能量位于能量轴上。将倒格子空间的原点由 Γ 点改为 K 点, E ( k )在狄拉克点附近近似为

其中, k =| k |,波数矢量 k 的模为倒格子空间中 K 点到狄拉克点处能量的原点的距离。
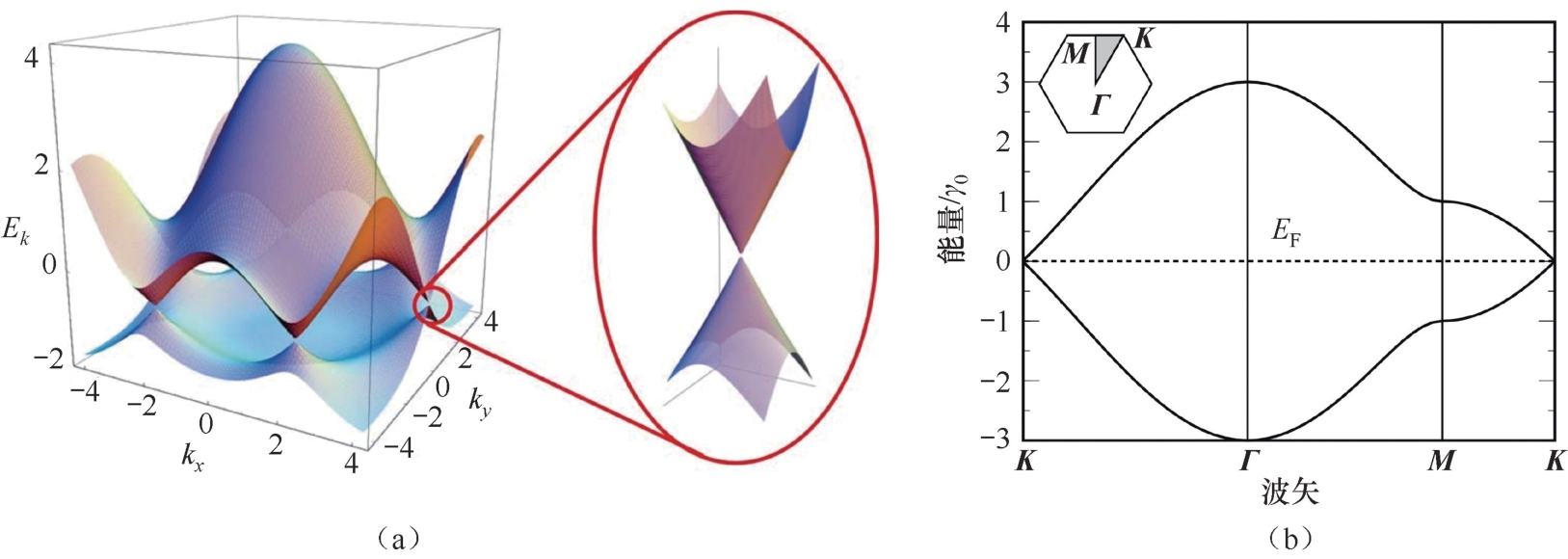
图2.2 (a)最近邻紧束缚模型得到的石墨烯的π电子能带结构。插图显示了在狄拉克点附近电子结构的放大图像 [25] 。(b)为在倒格子空间中沿 K → Γ → M → K 点的截面图像 [26]
与典型的二维电子系统的色散关系相比,石墨烯中的电子能量与波数是特殊的正比关系,而二维电子系统的色散关系是波数的抛物线能量函数。石墨烯电子的线性色散特性正是许多新特性的原因。利用式(2.7)导出狄拉克点附近的电子态密度为

将态密度 D ( E )与能量 E 积分,得到石墨烯载流子密度为

式中: E 为对应的电子或空穴的密度。如式(2.8)所示,态密度与能量成正比,在费米能量处为零。这意味着价带和导带间的能隙为零,因此石墨烯通常被称为零带隙半导体。
通过引入石墨烯层间相互作用,计算了多层石墨烯的电子结构,即两层以上石墨烯片的堆叠。多层石墨烯最稳定的结构就是石墨,如图2.3(a)所示,每片石墨以伯纳尔( AB )堆叠方式堆叠 [27] 。如前面提到的,石墨烯的碳原子可分为 A 和 B 两个位点。在 AB 堆叠结构中,第二层是平行放置在第一层下面的,以确保第一层 B 点( B 1 )与第二层的 A 点( A 2 )重合,第一层 A 点( A 1 )叠加在第二层蜂窝晶格六边形的中心。第三层的 A 和 B 点( A 3 , B 3 )与第一层位置( A 1 , B 1 )完全重合,以此类推,如图2.3(b)所示。因此, AB 堆叠的多层石墨烯的原始单元由两层石墨烯薄片组成,如图2.3(a)所示。
在 AB 堆叠结构中,相邻石墨烯薄片的最近邻碳原子的p z 轨道间的共振积分为 γ 1 ≈0.4eV,薄片间的距离为 c 0 /2=0.335nm。相邻石墨烯上紧邻的碳原子之间的相互作用用 γ 3 表示。在仅考虑层间最近邻相互作用的紧束缚近似的情况下,多层石墨烯与单层石墨烯的电子能带结构如图2.4所示。双层石墨烯的电子结构由四个能带组成,包括一对导带和价带,其中一对能带在狄拉克点(倒格子空间的 K 点)相互接触。在另一对中,导带的底部和价带的顶部位于 K 点,但它们沿垂直的能量轴从狄拉克点分别向上和向下移动了 γ 1 。因此,双层石墨烯也表现出相对于狄拉克点对称的电子能带结构,并具有与单层石墨烯类似的零带隙特征。然而,双层石墨烯的电子能与波数呈抛物线关系,线性色散特性消失。
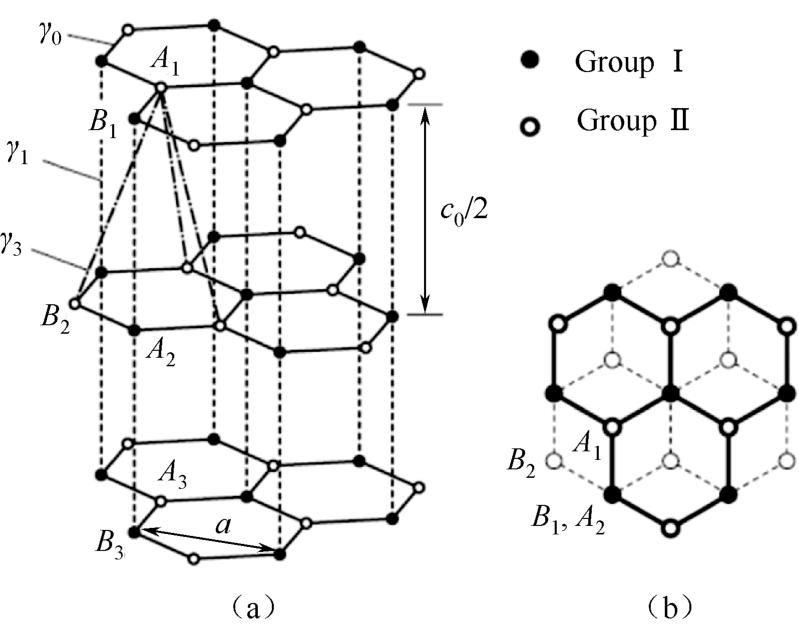
图2.3 (a)多层石墨烯的 AB (Bernal)堆叠结构;(b)奇数层(实线)、偶数层(虚线)的堆叠结构 [27]
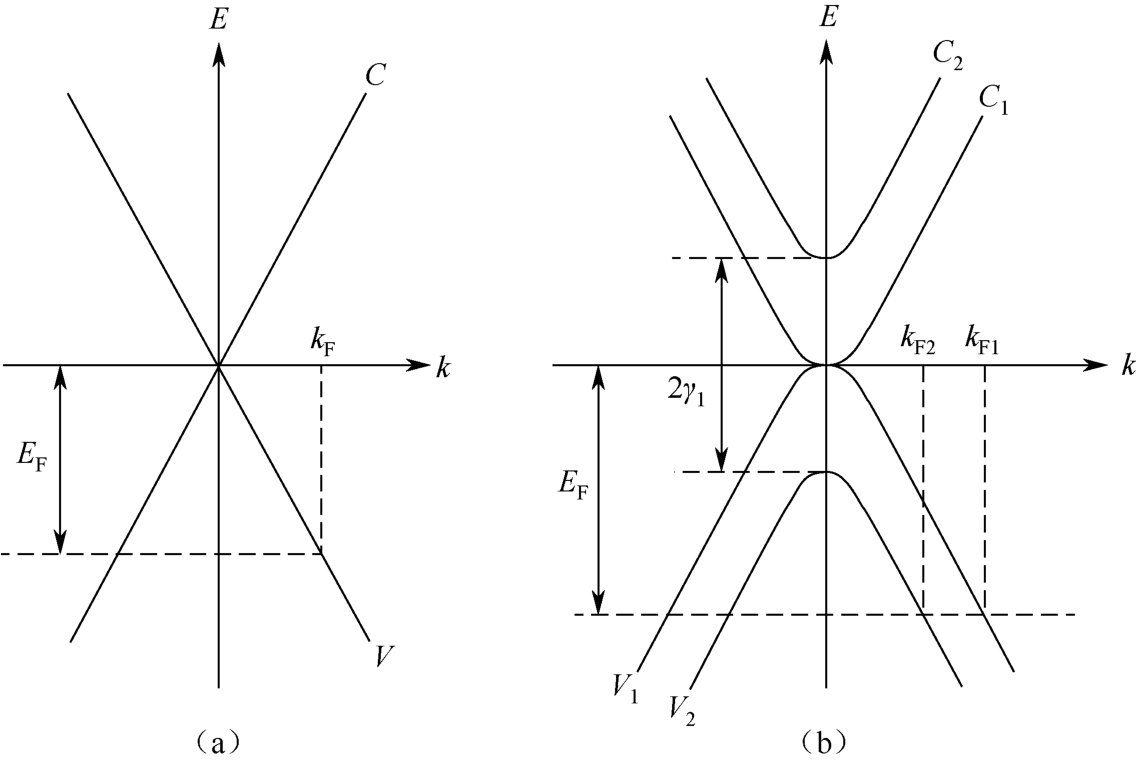
图2.4 单层石墨烯(a)和双层石墨烯(b)的能带结构,其中 C ( C 1 , C 2 )和 V ( V 1 , V 2 )分别表示导带和价带。 E F 为费米能级, k F , k F1 , k F2 表示 E F 电子态对应的费米波数 [23]
将单层石墨烯和双层石墨烯结合,可以很好地了解三层以上的多层石墨烯的电子结构。因此,偶数层为2 i ( i 为整数)的多层石墨烯具有与双层石墨烯类似的4 i 的抛物线电子能带。在奇数层(2 i +1)的石墨烯中,电子结构中出现了4 i 的抛物线能带(双层型)和两个与单层石墨烯类似的线性能带,如图2.5所示。因此,多层石墨烯的电子特性取决于其层数的奇偶性,可以通过单层或双层石墨烯的电子结构的贡献之和来理解。需要注意的是,这些结果只考虑了p z 轨道,并且在狄拉克点附近是有效的(通常在能量轴上的±0.1~0.2eV范围内),当电子能量离狄拉克点很远时,还需考虑s轨道和p轨道之间的杂化轨道的贡献。
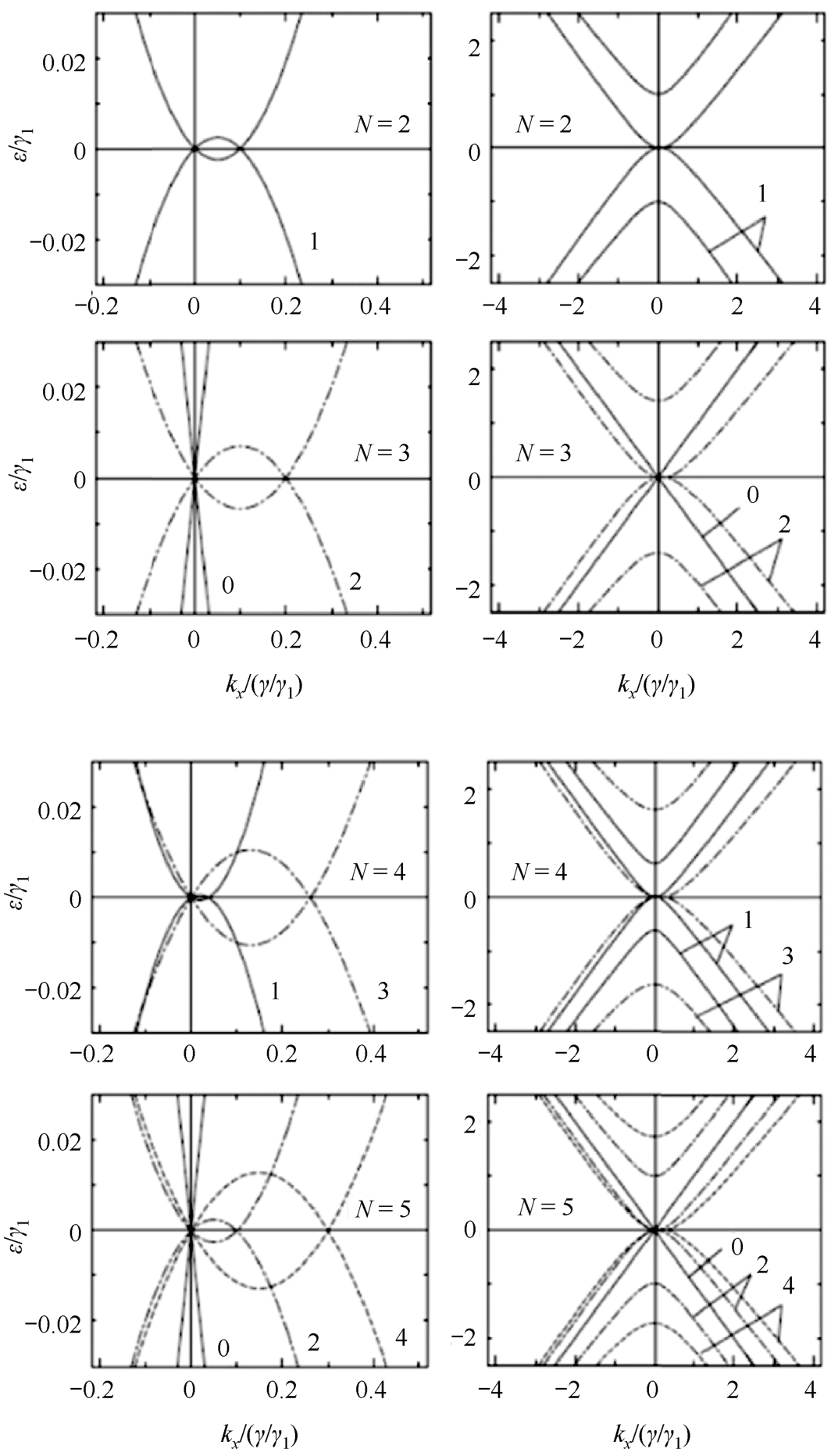
图2.5 多层石墨烯在 K 点附近的电子能带结构(层数 N =2,3,4,5),右图为左图的放大 [27]
如前所述,理想结构的石墨烯具有许多新颖的电子特性,这是因为它的拓扑结构稳定,且具有线性色散能带和零带隙属性,所以会抑制载流子散射,这也是石墨烯具有极高的载流子迁移率的原因。然而,现实中并不存在完美的石墨烯,杂质的引入、原子的缺失及晶格边缘的形态等都会在一定程度上改变电子结构,引起载流子散射。尤其是在晶体尺寸有限的石墨烯材料中,蜂窝晶格边缘的形态将发挥重要作用。
自20世纪90年代以来,M.Fujita等人已开始对石墨烯中边缘效应的理论进行研究 [28,29] 。从几何角度来看,石墨烯蜂窝状晶格的边缘可分为两种类型:锯齿形边缘和扶手椅形边缘,如图2.6所示。任意形状的边缘都可由这两种具有代表性的边缘的组合来描述。理论计算表明除具有理想石墨烯结构的价态π带和导电π * 带外,锯齿形边缘的石墨烯条带在狄拉克点还会出现非键π电子态的边缘态。边缘态几乎局限在石墨烯的边缘,并支配着石墨烯条带边缘的电子态。而扶手椅形边缘对狄拉克点周围的电子结构则没有显著影响。
考虑石墨烯蜂窝状晶格是由 A 、 B 碳位点组成的三角形子晶格的拓扑结构构成的,可以很容易理解锯齿形石墨烯条带出现边缘态的原因。如图2.6所示,锯齿形边缘仅由 A 或 B 位点中的一个点来终止,破坏了锯齿形边缘 A 和 B 位点的对称性。根据式(2.1)中的单电子哈密顿量,石墨烯的电子结构由共振积分连接的每个 A 和 B 位点上相邻碳原子的波函数之间的路径决定。碳原子网络的拓扑结构决定了薛定谔方程的解,所以即使石墨烯结构有缺陷,只要 A 和 B 位点依然保持对称性,也可以得到与理想石墨烯相似的电子结构,否则电子结构会发生显著的改变。子晶格对称性的破坏是锯齿形边缘出现边缘态的内在原因。
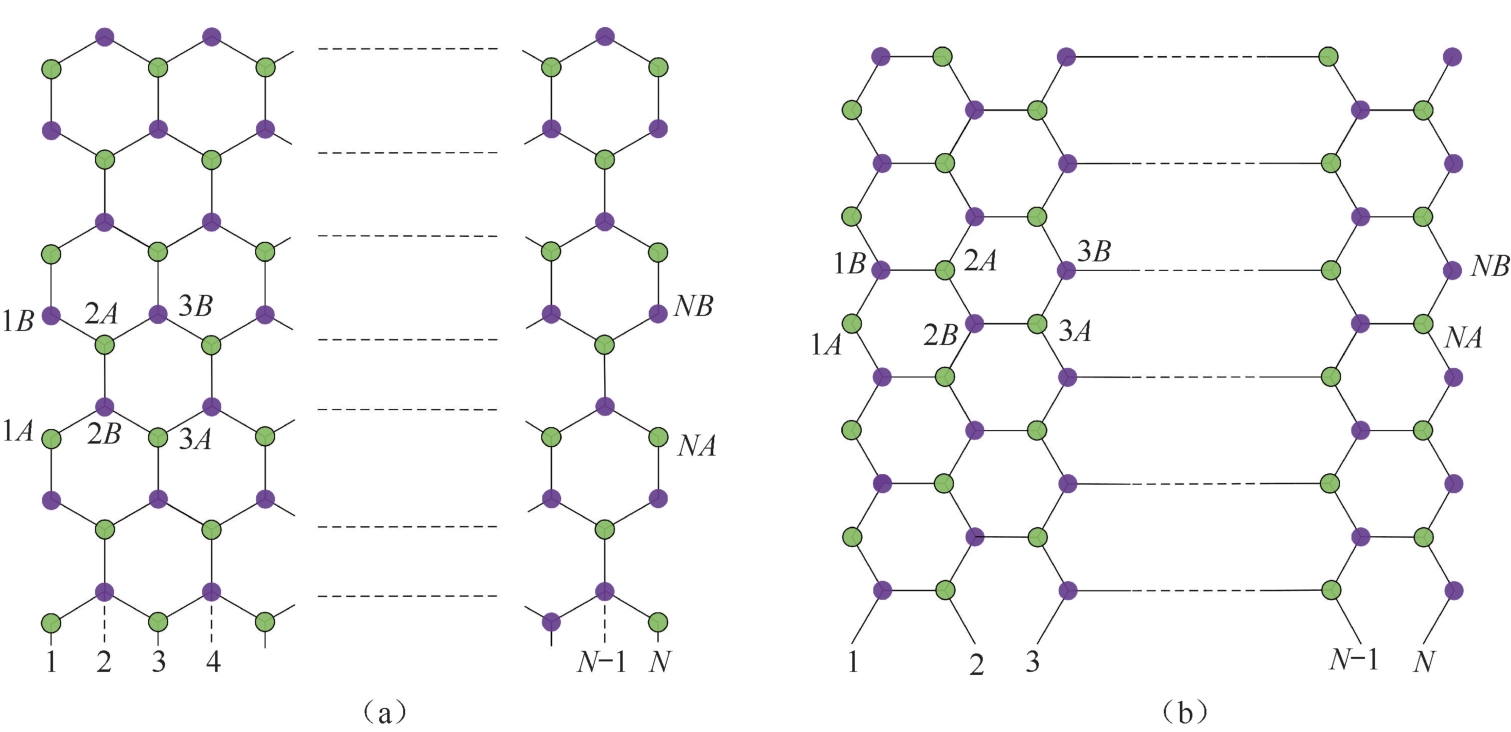
图2.6 (a)扶手椅形和(b)锯齿形边缘的石墨烯蜂窝状晶格 [23]
图2.7所示为在 N =200个单位晶胞的石墨烯条带中,通过紧束缚近似计算的条带的14个能级,锯齿形纳米带呈现了扶手椅形中没有的零能量模式。这个零能量的带是石墨烯条带边缘的表面态。它们之间的相互作用可以导致石墨烯边缘附近出现电子间隙和磁态。然而,从实验的角度来看,石墨烯纳米带的边缘具有高度的粗糙度。这种无序边缘会显著改变边缘态的性质,导致量子霍尔效应的安德森局域化和异常,以及库仑封锁效应等。
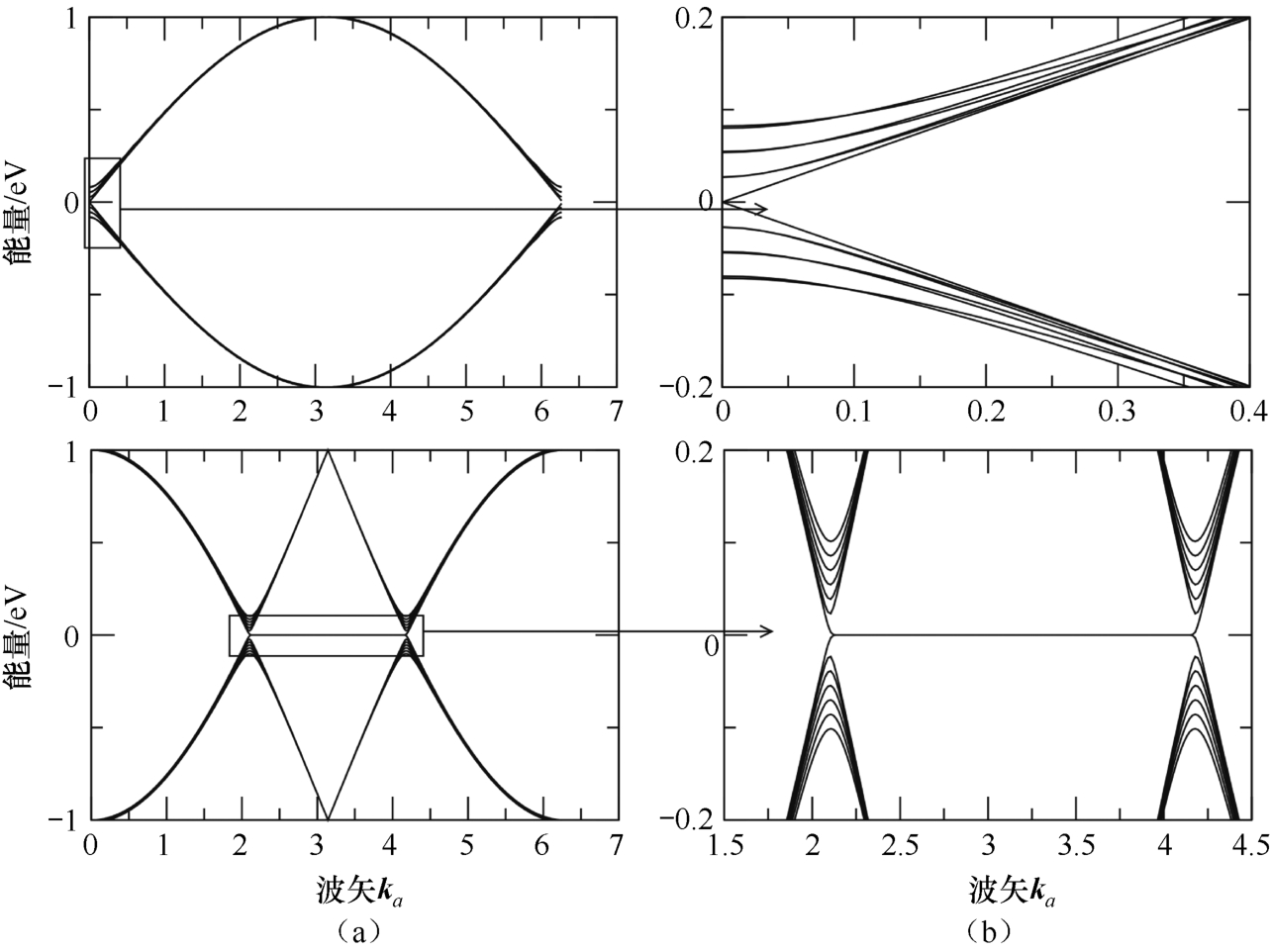
图2.7 石墨烯纳米带的电子色散。(a)紧束缚近似计算的扶手椅形(顶部)和锯齿形(底部)边缘的纳米带的能量谱;纳米带宽度为 N =200个单位晶胞;(b)低能态的放大图 [25]
围绕狄拉克点 K 和 K′ 的狄拉克哈密顿量可由式(2.1)给出,其对应的子格 A 和子格 B 在实空间中的波函数分别为
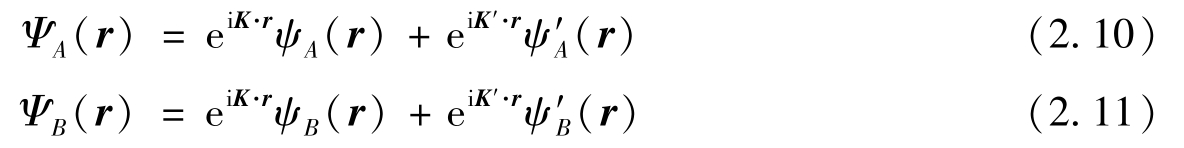
式中: ψ A 和 ψ B 均为哈密顿量的旋量波函数的分量。假设纳米带的边缘平行于 x 轴,则平移对称性保证旋量波函数可以写成

与哈密顿量的旋量方程相似,其中 φ A 和 φ B 为旋量。对于锯齿形边缘,条带边缘(位于 y =0和 y = L 处,其中 L 为条带宽度)的边界条件为
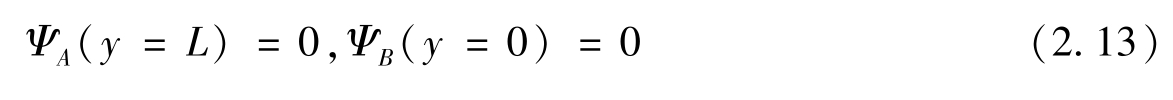
所以
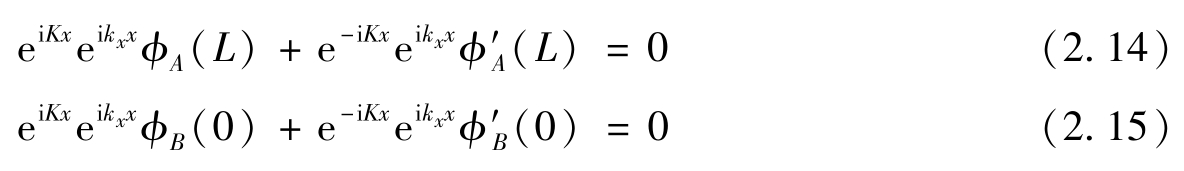
对于任意 x 边界条件,式(2.14)和式(2.15)都满足,则要求 K 点周围的特征函数可以表示为
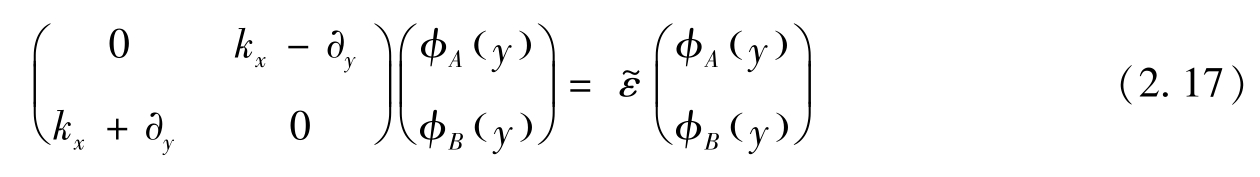
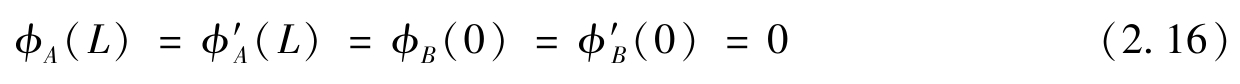
其中,
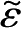 =
ε/v
F
,
ε
为能量本征值。本征问题可以写成两个线性微分方程的形式,即
=
ε/v
F
,
ε
为能量本征值。本征问题可以写成两个线性微分方程的形式,即
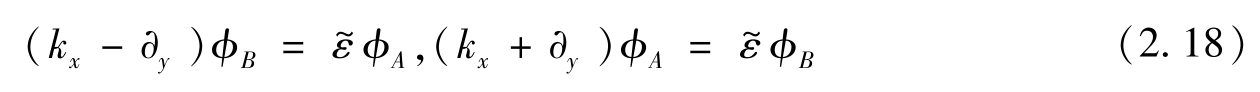
式(2.18)第一项两边同时乘以算子( k x +∂ y )得到

解为

φ A 可计算如下:

得到特征能为
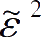 =
=
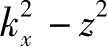 。锯齿形边缘的边界条件要求
φ
A
(
y
=
L
)=0和
φ
B
(
y
=0)=0,得
。锯齿形边缘的边界条件要求
φ
A
(
y
=
L
)=0和
φ
B
(
y
=0)=0,得
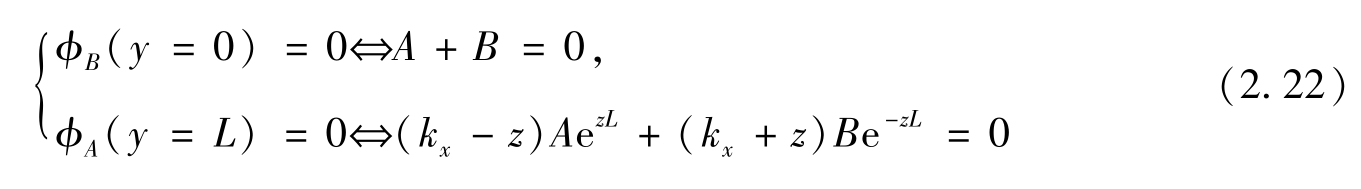
则特征值方程为

当 k x 为正时,式(2.23)中的 z 有实解,这些解对应于石墨烯条带边缘的表面波(边缘态)。除了 z 的实数解,式(2.23)还支持 z =i k n 的复数解,即

式(2.24)的解对应石墨烯条带中的约束模式。在狄拉克点 K ′附近应用相同的方法,可以得到另一个不同的特征值方程,即

当 k x 为负时,方程支持 z 的实数解。因此,动量在狄拉克点 K ′附近时,条带具有负 k x 的边缘态。和 K 的情况一样,系统也支持约束模式,如

当 t′ =0时,锯齿形条带的边缘态是非色散的(局限于真实空间)。当电子—空穴对称性被打破时( t′ ≠0),这些边缘态就会变成具有费米速度 v e ≈ t′a 的色散态。
现在考虑沿 y 方向有一个扶手椅形边缘的纳米带。条带边缘的边界条件(位于 x =0和 x = L 处,其中 L 为条带宽度)为
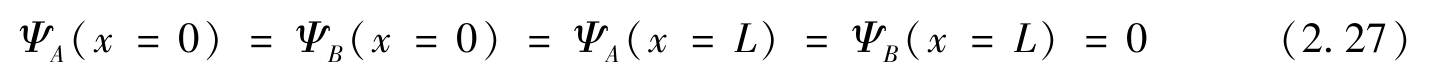
平移对称性保证了哈密顿量[式(2.1)]的旋量波函数可以写成

边界条件可以写成
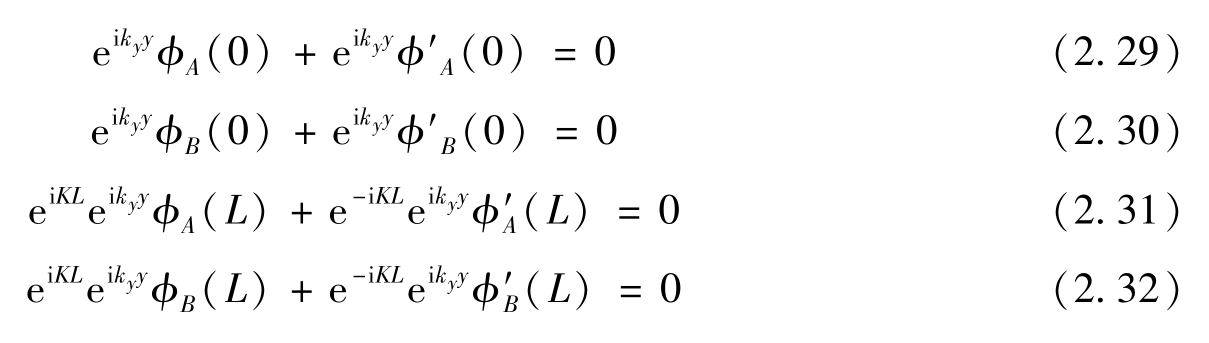
满足任意 y 的条件是
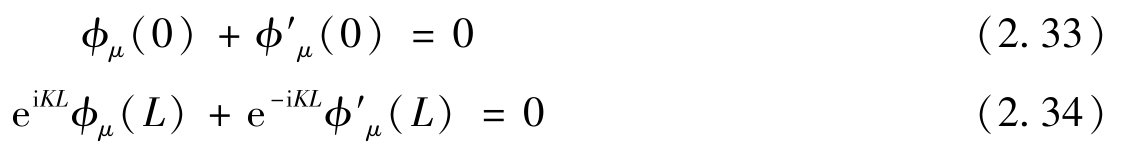
其中,
μ
=
A
,
B
。很明显,这些边界条件混合了两个狄拉克点的状态。如前所述,函数
φ
B
和
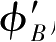 服从二阶微分方程[式(2.19)](用
x
代替
y
),函数
φ
A
和
服从二阶微分方程[式(2.19)](用
x
代替
y
),函数
φ
A
和
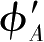 由式(2.21)确定。式(2.19)的解为
由式(2.21)确定。式(2.19)的解为

应用边界条件式(2.33)和式(2.34),可以得到
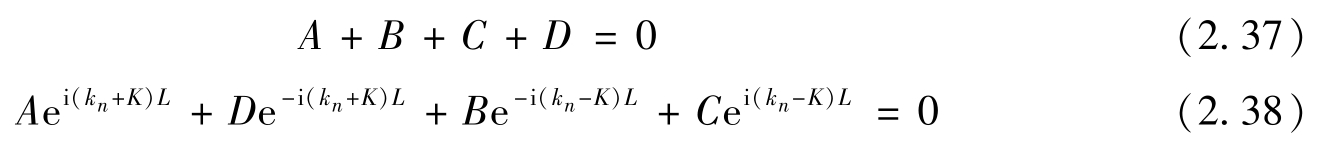
满足边界条件则需

使得sin[(
k
n
+
K
)
L
]=0。因此,
k
n
及本征能量
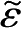 的值允许为
的值允许为

在这种情况下不存在表面态。